圆环形压电振子振动分析与实验研究

张代治，徐安俊，田晓超

(长春大学 机械与车辆工程学院，长春 130022)

随着压电材料的不断发展，由其构造的压电振子成为近代以来新型驱动器之一。压电振子性能也在不断提高和完善，具有控制精度高、响应速度快、无磁干扰等特点，变形精度精确到微米级或纳米级，常被作为高精密驱动器使用[1]。压电振子激励振动系统工作，工作的机构有多种形态，这些状态相互耦合相互影响，直接影响着压电振子性能，因此，研究压电振子的振动形态和特性是十分必要的。

Dobruki等人利用有限元法对对称形式布置的压电振子以及周边固定支承和简支边界的压电振子进行了动态和静态分析，同时推导出了相应的数学表达式[2]。阚君武等人利用瑞利能量法对三叠片换能器进行了弯曲振动分析，探究结构尺寸参数对换能器的影响，为压电换能器的选用与优化设计提供了理论依据和技术参考[3]。孙晓峰等人利用弹性力学相关知识论对圆形双晶片压电振子进行了分析，推导出了周边固定支撑方式的压电振子弯曲振动方程[4]。

利用弹性力学、ANSYS软件仿真及实验测试等手段对圆环形压电振子进行了数值计算、仿真分析与实验测试，为压电振子的设计优化和应用提供理论依据和技术参考。

1 结构设计与振动方式

圆环形压电振子结构示意图如图1所示。该结构主要由三层叠片组成，金属基板两侧帖置压电陶瓷，中间具有通孔结构，采用的支撑方式为周边固定支撑式，中间金属基板的直径要大于陶瓷片的直径，金属基板多出的部分用于周边固定支承，其结构如图2所示。

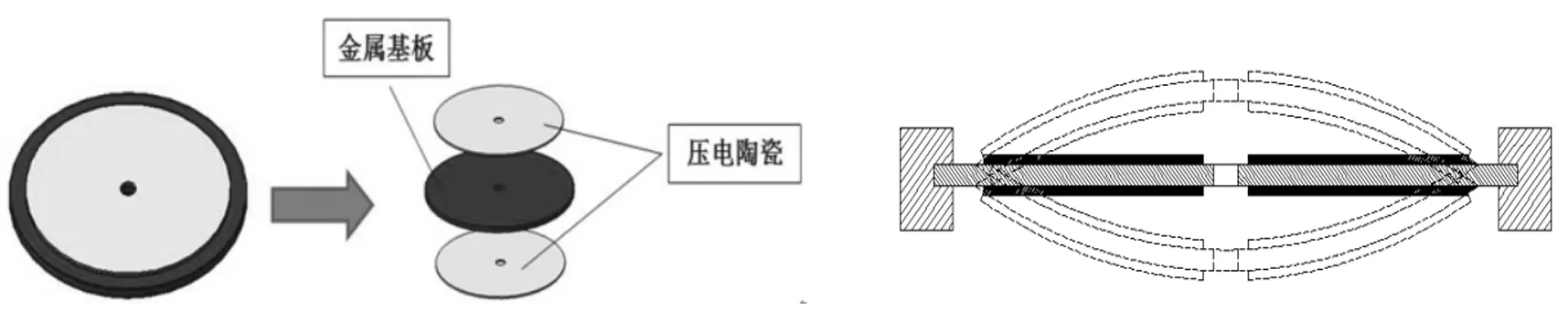
图1 圆环形压电振子结构图 图2 圆环形压电振子支承方式示意图

圆环形压电振子为系统提供持久振动的激振力。中间通孔结构连接传振机构，有效地将力和位移有效的输出，其结构示意图和三维图如图3所示。

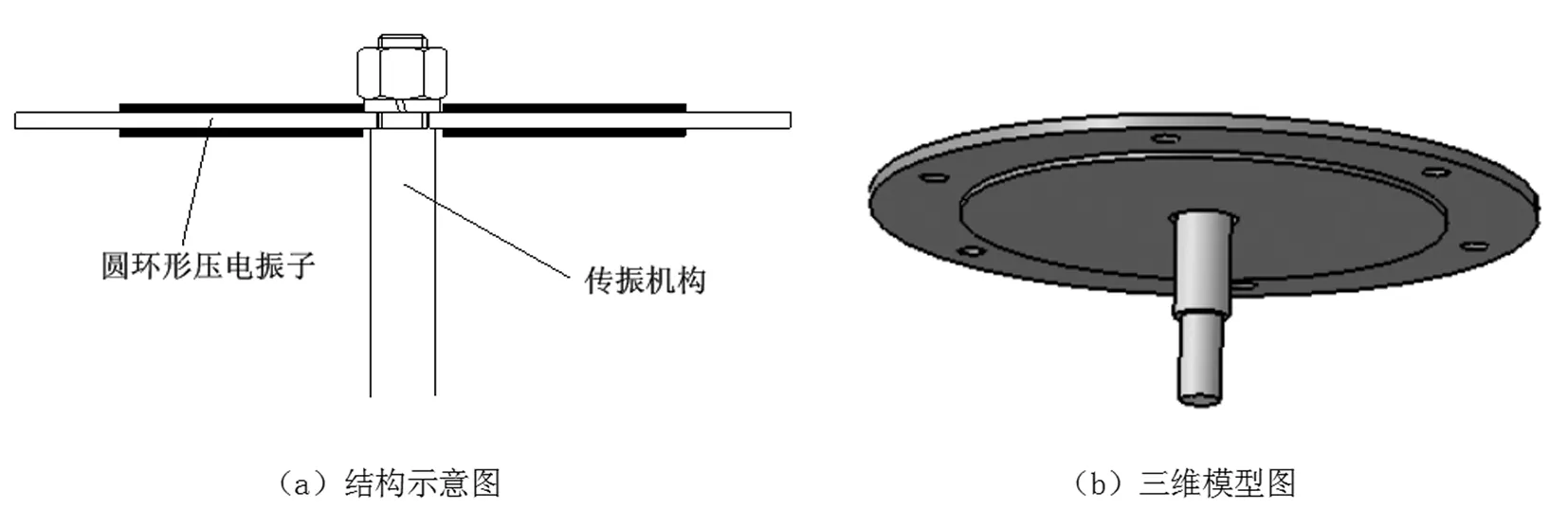
图3 圆环形压电振子连接示意图

2 理论分析

由于中间传振机构输出压电振子提供的激振力，周边固定，中心处受到集中荷载，示意图如图4所示。

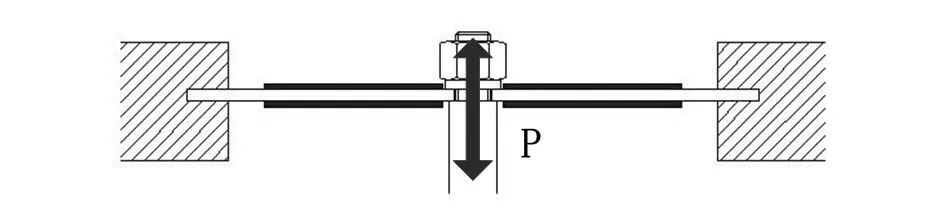
图4 圆环形压电振子受集中载荷示意图

设集中荷载P，则距中心为r处的总剪力与集中载荷P值相等且方向相反，即

2πrQr=-P，

(1)

其中，Qr用极坐标表示为：

(2)

将式(2)代入式(1)，得：

(3)

将上式积分后得：

(4)

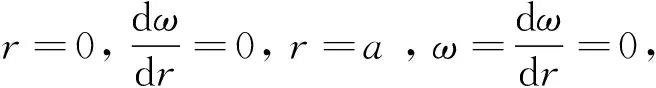
(5)

将式(5)代入式(3)，得：

(6)

则圆环形压电振子中心点的最大挠度在中心r=0处为：

(7)

等效集中力为：

(8)

上式中D为圆环形压电振子的等效刚度，主要为金属基板和压电陶瓷结合的等效刚度，表示为：

(9)

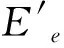
(10)

(11)

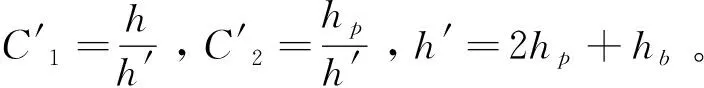
单晶片压电振子中压电陶瓷和金属基板的复合部分的等效弹性模量Ee和等效泊松比υe[5]为：

(12)

(13)

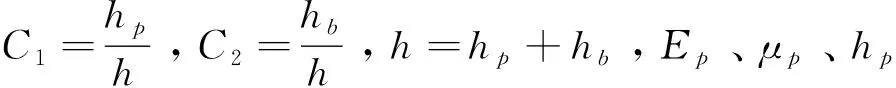
圆环形压电振子的尺寸和结构参数如表1所示，计算结果为圆环形压电振子的最大挠度ωbm为34μm，最大集中输出力为85N。

表1 圆环形压电振子的参数

3 模态分析

圆环形压电振子的材料属性如表2所示，尺寸参数如表1所示。利用ANSYS软件对圆环形压电振子进行振动形态和固有频率的分析。首先要进行圆环形压电振子三维建模的建立，然后采用映射网格划分，压电陶瓷采用的单元类型为SOLID5，金属基板采用的单元类型为SOLID45。

表2 圆环形压电振子材料属性

压电陶瓷的参数如下：

得到四阶压电振子振型，如图5所示。

图5 圆环形压电振子四阶振型

从图5可以看出，圆环形压电振子中间红色区域振幅最大，一阶振型符合压电振子工作时的形态，压电振子的固有频率为3152.8Hz，最大位移为35.9μm。

4 实验测试

圆环形压电振子振动位移测试装置如图6所示。压电振子在信号驱动器驱动下往复弯曲振动，压电振子振动位移通过激光测微仪进行测量，位移显示器跟踪压电振子的振动位移及时输出。利用阻抗分析仪对压电振子固有频率进行测试，测试装置如图7所示。

图6 位移测试装置图 图7 固有频率测试装置图

将信号驱动器的电压调至200V，改变信号驱动器的驱动频率，测试圆环形压电振子的中心点变形量，测试结果如图8、图9所示。从可以看出，圆环形压电振子的共振频率为3.3kHz，最大变形量为32.5μm。

将驱动信号调节至压电振子的共振频率3.3kHz，改变电压值，得出圆环形压电振子中心点位移和电压的关系如图9所示。可以看出，圆环形压电振子的中心点变形量与外界驱动电压呈较好线性关系，随驱动电压增加而增大。经阻抗分析仪测得压电振子固有频率为3200Hz。

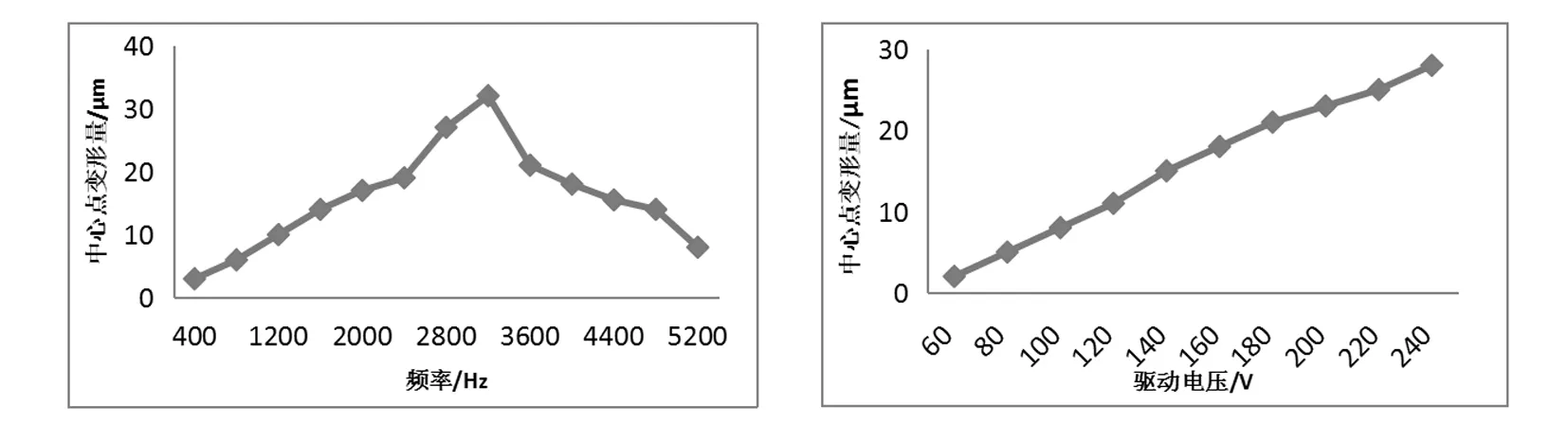
图8 压电振子中心变形量与驱动频率关系图 图9 中心点变量与驱动电压关系图

压电振子中心变形量与驱动频率关系测试结果表明，圆环形压电振子中心点的变形量可以通过改变外界驱动电压和驱动频率来调节控制。通过压电振子理论分析、仿真分析与实验测试，得到压电振子的共振频率结果如表3所示。

表3 圆环形压电振子位移分析值 μm

通过以上数据比较可知，理论分析、仿真分析和试验测试得到的共振频率值基本上是相吻合的。但存在一定的误差，主要原因有：①理论建模分析时，忽略了压电陶瓷和金属基板之间粘接力的影响，模型过于理想化；②测试圆环形压电振子中心点变形量时都是人为操作，测试结果与实际数值存在一定的误差；③利用阻抗分析仪测试圆环形压电振子阻抗时，受到周围环境影响，如温度、工作台的稳定性等。

5 结语

我们利用弹性力学、ANSYS软件仿真及实验测试等手段对圆环形压电振子进行了数值计算、仿真模态与实验分析。分析了驱动电压和驱动频率对压电振子变形量的影响，圆环形压电振子在共振状态下中心点变形量最大。通过实验测试，在外界驱动电压为200V，谐振频率为3200Hz情况下，位移最大值为32.5μm。与仿真分析和理论推导结果基本吻合，误差较小，验证了理论分析的正确性与合理性，为圆环形压电振子的设计优化与应用提供了理论依据和技术参考。