基于实测数据的固体火箭发动机粘接界面振动损伤分析

刘 磊，李高春，李金飞，王 鑫，宋佳明

(海军航空大学 岸防兵学院，烟台 264001)

0 引言

固体火箭发动机作为导弹的助推动力装置，其性能的优劣往往决定着导弹在战备值班时能否具备有效威慑、作战时能否安全使用。发动机内的装药在浇注成型后，无法像机械部件一样进行拆装和更换，一旦失效就意味着发动机报废；其本身作为粘弹性材料对承受的载荷具有“记忆”，长时间受载时会产生蠕变和应力松弛现象，直接导致力学性能退化，降低发动机寿命。作为装药组成部分的推进剂药柱和推进剂/衬层粘接界面成为制约固体火箭发动机使用寿命的关键因素。

近年来，舰载和艇载导弹在海洋环境下要求的值班周期更长，面临的载荷更加严酷。海上值班时，立式贮存的固体火箭发动机受到重力载荷和海洋波浪引发的持续振动载荷作用，在推进剂/衬层粘接界面处产生千帕级的剪切应力[1]。从粘接界面剪切试验结果看，推进剂与衬层界面破坏时剪切应力达到兆帕级，瞬时剪应力不会对粘接界面结构造成直接破坏，但长期交变应力引起的结构疲劳损伤不容忽视。国内外针对固体火箭发动机装药在振动载荷下的损伤做了一定的研究工作[2-5]。曲凯[2]通过有限元分析法，认为某固体火箭发动机在海上值班一年时的贮存寿命比洞库存储寿命低8.62%。张波[1]利用疲劳试验与有限元计算结合的方法，得出舰载条件下发动机连续值班一年使用寿命至少降低15.4%的结论。以上研究中，输入的振动载荷均是依据舰船耐波性理论和发动机运动与受力关系仿真得到的[6]，该方法为缺少发动机实测振动载荷数据时获取固体发动机海上值班的横摇、纵摇、升沉运动规律提供了一条有效途径。为掌握舰船在海上值班时固体火箭发动机承受的真实载荷情况，李金飞[5]对舰艏甲板位置振动参数进行了间断性监测，发现两种海况下三轴加速度功率谱密度最大值均在较小的频率范围内。当前，国内针对舰载固体发动机的环境监测及环境影响研究取得了一定的成果，但对艇载发动机承受环境载荷情况并不明确，对艇载发动机损伤规律缺乏深入的研究。

本文以某立贮式固体火箭发动机为研究对象，建立了发动机全尺寸模型，利用有限元软件模拟了固化降温和振动两个连续过程，得到了推进剂/衬层粘接界面的剪应力分布；依据三点雨流计数和Miner线性累积损伤理论对危险点处的疲劳损伤进行了计算，对特定海情下固体火箭发动机值班时的寿命损伤情况展开了分析。

1 振动数据采集与处理

采用环境监测装置对导弹贮运箱内的振动载荷进行监测，考虑到长期监测的需求与存储容量的限制，对振动数据采用间断性采集。传感器三个方向的坐标设定符合笛卡尔坐标系，X轴表示平台纵摇方向，Y轴表示横摇方向，Z轴表示垂向。部分采集的三轴加速度信号如图1所示。

由于传感器对环境变化比较敏感，温度等环境因素的变化可能造成零点漂移，使信号产生长周期趋势项；同时，采集的信号可能叠加随机高频噪声干扰信号，使振动曲线出现尖端毛刺。为消除趋势项和干扰信号的影响，首先要对获取的原始数据依次进行消除趋势项处理和平滑处理。消除趋势项采用较为常用的多项式最小二乘法[7]。对于振动采样数据点{xk}(k=1,2,3,…,n)，首先设置一个多项式函数：

(k=1,2,3,…,n)

(1)

(i=0,1,2,…,m)

(2)

其中，m为设定的多项式阶次，m≥2时趋势项为曲线。处理振动信号时，设置m=3。

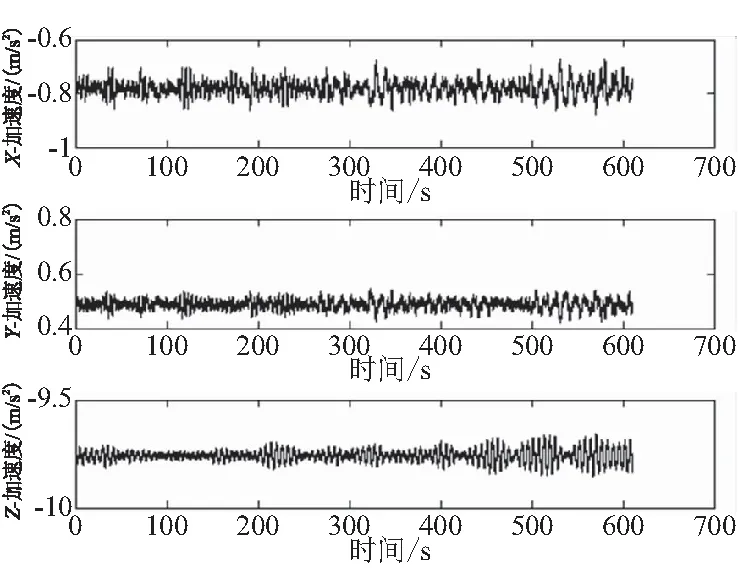
图1 振动采集数据

平滑处理方法主要有直线滑动平均法和五点三次平滑法[8]。因直线滑动平均法所需滑动次数较少，且更方便进行编程计算，所以选用五点滑动平均法。其计算公式为

(3)

选取某特定海情下值班时300 s的振动监测数据进行处理。振动原始信号与处理后的信号分别如图2所示。

由图2显示的数据可知，z轴采集的加速度数据包含重力加速度g，理想曲线应以y=-g为基线，但x轴和y轴数据曲线的基线均偏离零轴，认为选取的信号存在趋势项。经过数据处理后，振动曲线形状基本保持不变，三轴的振动基线均变为y=0。对比图2的两种信号，经过数据处理后，振动曲线由粗糙变得光滑，且峰谷部位的毛刺得到有效剔除。

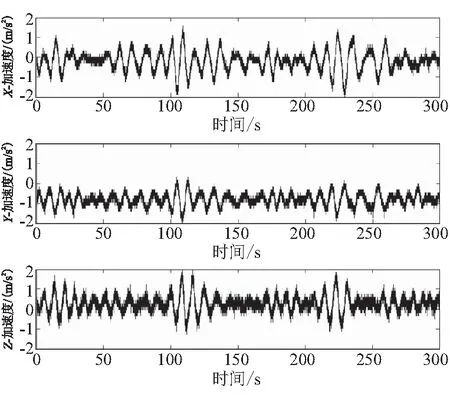
(a)原始信号

(b)处理后的信号

2 基于实测数据的有限元计算

2.1 固体火箭发动机模型

为探究实际海洋环境下重力与振动耦合作用引起的粘接界面应力分布情况，利用有限元软件abaqus对固体火箭发动机进行分析。考虑到发动机粘接界面不同环向位置受载状态可能不同，建立某型发动机全尺寸模型。发动机结构剖视图如图3所示。

图3 发动机结构剖视图

固体火箭发动机模型共有壳体、衬层、推进剂药柱和人工脱粘层等主要组成部分。分别设置4种材料的热导率、密度、弹性参数、膨胀系数及比热容，参数值如表1所示。

推进剂为粘弹性材料，其弹性模量E(t)以Prony级数形式表示[9]：

E(t)=1.79+1.65e-25t+2.05e-2.5t+

3.04e-0.25t+3.88e-0.025t

(4)

式中t为时间，s；E为弹性模量，MPa。

设置边界条件时，分别设置3组绑定约束：壳体内表面-衬层外表面、衬层内表面-推进剂药柱外表面、壳体内表面-人工脱粘层外表面。人工脱粘层和药柱接触表面不设置约束，目的是释放药柱头部和尾部处的集中应力。

表1 发动机材料参数

2.2 固化降温过程模拟

为获得固体发动机浇注后由高温到环境常温承受的原始应力，首先使用温度-位移耦合模块模拟发动机固化降温过程[10]，将固化降温的计算过程设为分析步1。实际降温过程中壳体材料变形量很小[11]，设置壳体为固定约束。在较长的固化降温时间里，推进剂药柱由于承受热应力而产生变形，图4分别显示了固化降温后固体发动机整体和局部的位移场。可看出，装药头部和尾部变形量最大，中孔段变形量最小，药柱由外向内变形量逐渐增大。

从药柱两端位移分布图看，固化降温过程中药柱两端发生收缩变形，药柱端面与人工脱粘层脱开，产生一定的间隙。其中，药柱头部和尾部前缘凸环形处变形量最大，与壳体的最大间隙达到30.7 mm；两翼的变形量仅次于凸环形处，翼端最大位移达到26.9 mm。

为了探究推进剂/衬层粘接界面的初始应力分布状况，在后处理结果中查看图5所示的推进剂药柱外表面最大剪应力云图。Tresca屈服准则符合第三强度理论，认为最大剪应力是引起材料屈服的主因素，云图中显示的是粘接界面处的最大剪应力τmax。可以发现，界面轴向最大剪应力呈梯度分布，由两端到中间部位逐渐递减。界面头部和尾部是应力最集中的两个部位，固化降温后的原始最大剪应力分别达到53.7 kPa和60.7 kPa。提取两个部位剪应力最大值点的时程曲线如图6所示。在固化初期剪应力增长较快，随时间增加剪应力增长趋势放缓，固化末期接近于恒定值。对固化降温期间剪应力时程曲线进行拟合，得到幂函数方程：

τ=a·tb+c

(5)

式中τ为剪应力，kPa；t为固化时间，s；a、b、c均为拟合系数，各系数值如表2所示。

两条曲线的拟合公式相关系数分别达到0.992和0.991，拟合精度较高。

(a)发动机整体位移场 (b)头部位移场 (c)尾部位移场

图5 粘接界面剪应力分布

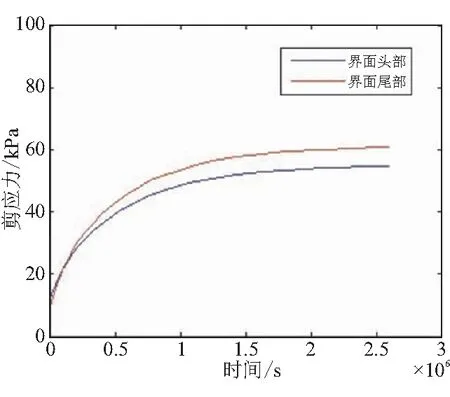
图6 界面头部和尾部剪应力时程曲线

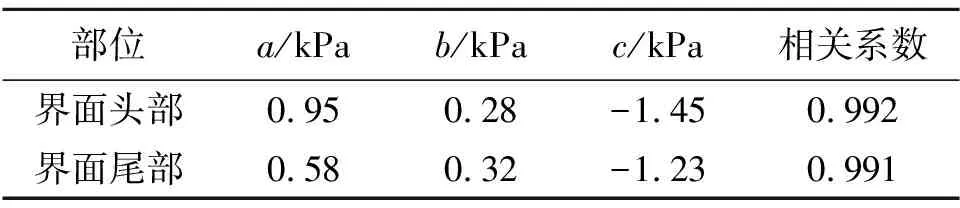
部位a/kPab/kPac/kPa相关系数界面头部0.950.28-1.450.992界面尾部0.580.32-1.230.991

2.3 振动过程模拟

2.2节中已经将固化降温的计算过程设为分析步1，现将振动的计算过程设为分析步2，即将固化降温的计算结果作为振动的初始条件。由于固化降温过程中发动机壳体设置了固定约束,振动开始时刻可认为发动机位移为0。若对发动机模型直接施加振动加速度载荷，由于重力加速度的叠加作用，在模拟计算时发动机整体做下沉运动，与实际运动状况不符。为了模拟重力和振动耦合作用下的发动机真实运动，将处理后的振动加速度数据转化为模型的位移数据，转化方法采用频域二次积分法[7]，处理得到的位移数据如图7所示。

将位移数据作为输入载荷施加于发动机壳体，同时对整个发动机模型施加竖直向下的重力加速度g，以0.2 s的输出结果作为一帧，计算300 s时程下发动机粘接界面应力变化。图8显示了某一振动时刻粘接界面的剪应力云图，轴向剪应力分布情况相比初始应力发生了明显变化：界面尾部剪应力降低，剪应力主要集中于界面头部。由于中部始终是粘接界面剪应力最小的部位，所以重点关注界面两端的剪应力变化情况，提取头部和尾部剪应力最大值点的时程变化数据，如图9所示。振动前15 s内剪应力幅值发生较为剧烈的变化，15～300 s内振动幅值趋于平稳，产生相对理想的波形。分析该现象产生的原因，在振动开始时刻，发动机由静止产生加速运动，发动机内大质量推进剂药柱由于惯性作用，其内部运动与壳体不完全同步，药柱自由端产生不稳定大变形，因此导致应力剧烈变化。随着振动时间增加，药柱呈现较为稳定的类似周期性的变形，因而应力也趋于稳定变化。固化降温后，界面头部取值点原始剪应力为54.7 kPa，稳定振动后，剪应力变化基线的纵坐标提高到63.5 kPa；界面尾部取值点原始剪应力为60.7 kPa，稳定振动后，剪应力变化基线纵坐标降低到40.2 kPa。将界面头部的取值点设为整个发动机粘接界面的危险点。

图7 位移曲线

图8 某一时刻粘接界面剪应力云图

3 振动疲劳损伤计算

3.1 雨流计数

国家行业标准JB 4732—1995[12]中采用了S-N曲线进行材料的疲劳寿命分析。为了应用S-N曲线和损伤理论进行疲劳分析，需要使用计数法将应力时程转换为载荷块构成的应力谱[13]。在多种计数法中，雨流计数法因具有与材料应力-应变特征相符的优点而广泛应用。文中采用三点循环计数法进行雨流计数，其计数原理是检查每3个连续的点，假设3个连续应力点分别为S1、S2、S3，定义两个连续区：ΔJ1=|S1-S2|，ΔJ2=|S2-S3|。如果ΔJ1≤ΔJ2，则提取一个循环，直到所有数据点提取完毕。

图9 危险点处的剪应力时程曲线

提取危险点处稳定振动共计约285 s的剪应力数据，如图10所示。将数据代入到循环程序中进行计数，计数结果显示为图11所示的雨流直方图。其中，x轴代表幅值，y轴代表均值，z轴代表统计次数。

图10 提取的285 s有效振动数据

3.2 疲劳累积损伤计算

对材料的剪应力时程进行雨流计数后，通常要结合材料本身的疲劳特性及疲劳损伤理论来进行疲劳损伤的预估。国内外针对疲劳损伤规律展开了大量研究，提出了多种累积损伤理论。其中，Miner线性疲劳累积损伤理论(简称Miner理论)以其简单方便的优点，更广泛地用于工程计算。Miner理论忽略加载次序对试件的影响，损伤计算公式如下：

(6)

式中k为幅值的级数；ni为第i级幅值对应的累积次数；Ni为第i级幅值对应的疲劳破坏次数。

图11 雨流直方图

当损伤累积值达到1时，认为材料发生疲劳破坏。

当前，固体发动机领域尚未具备关于界面剪应力的疲劳损伤试验标准，国内学者主要参照标准QJ 2038.2—91和GB/T 1455—2005来进行界面剪切应力强度试验[1-2]，探究推进剂/衬层粘接界面的损伤演化规律。通过仿真数据与试验测试数据对比，固体发动机在海洋环境下承受的瞬时剪应力远小于临界破坏值，在损伤研究时，应充分考虑小交变应力的累积效应。文献[2]通过定应力变程疲劳试验，得到了推进剂/衬层粘接试件Δτ-N疲劳损伤方程：

(7)

式中 Δτ为粘接界面处的剪应力增量，与雨流矩阵中的幅值相对应，MPa；N为特定剪应力增量对应的疲劳破坏次数。

将雨流计数结果代入式(7)中，可得到每个闭循环剪应力幅值对应的疲劳极限寿命，再将每个极限寿命的倒数代入式(6)进行累加计算，得到285 s时间段内危险点处累积损伤值为1.808×10-6，以该时间段内的累积损伤值作为基元，可得到在该特定海情下连续值班一年造成的粘接界面振动损伤为14.84%。

4 结论

(1)固化降温过程中，推进剂药柱会发生收缩，头部和尾部端面与人工脱粘层脱开，与壳体之间产生间隙，最大间隙达到30.7 mm。推进剂/衬层粘接界面的剪应力在轴向呈阶梯形分布，剪应力集中于界面头部和尾部。固化过程中发动机界面剪应力的变化可以由幂函数方程τ=a·tb+c较精确地表述。

(2)以固化降温计算结果作为发动机振动的初始条件，考虑重力载荷的作用，振动初始15 s内剪应力变化不稳定，曲线产生较剧烈波动；振动15～300 s内振动较稳定，界面危险点处剪应力呈现出以y=63.5 kPa为基线的类周期性波动。稳定振动时，推进剂/衬层粘接界面头部承受的剪应力最大，界面尾部承受的剪应力相比初始值有所下降。

(3)某特定海情下，某立贮式固体发动机连续值班一年时，由重力和振动因素造成的粘接界面疲劳损伤为14.84%。

由文献[1]可知，不同海情下发动机累积损伤存在较大差异，未来有必要进行固体发动机典型振动载荷谱的编制，从而进一步对发动机在长时间海洋值班条件下的界面损伤进行更精确的评估。