基于粘弹性VCFEM的复合固体推进剂等效松弛模量预示方法研究

2019-07-31申柳雷李海阳申志彬

固体火箭技术 2019年3期

申柳雷，李海阳，申志彬

(国防科技大学，长沙 410073)

0 引言

复合固体推进剂等效松弛模量是进行固体发动机药柱结构完整性分析重要的输入参数之一，很多学者针对该问题进行了长期研究。彭威等基于Eshelby-Mori-Tanaka等效模型，分别推导了含球形[1]和非球形[2]颗粒的推进剂等效松弛模量，认为推进剂的等效模量可表示为增强系数与基体相松弛模量的乘积形式，并给出了增强系数与体积分数、颗粒形状及基体材料参数的关系；李高春等[3]结合Mori-Tanaka模型和有限元法，计算了含两种粒径颗粒的推进剂等效模量；赵玖玲等[4]研究了键合剂和AP级配对推进剂等效模量的影响规律；张建伟等[5]采用分子动力学和有限元法，分析了颗粒体积分数和基体相材料特性与推进剂的松弛模量的联系。

复合固体推进剂的力学性能主要由各组分的材料特性、夹杂相的含量与级配等细观特征参数所决定。采用传统的位移有限元法从细观层面预示推进剂力学性能时，需要划分稠密的有限元网格，其带来的巨大计算量难以满足高效率的设计需要。美国Ohio州立大学的Ghosh等[6]提出了Voronoi单元有限元法(Voronoi Cell Finite Element Method,VCFEM)，该方法基于杂交应力元的思想，利用Voronoi多边形进行有限单元离散，只需要用少量单元，就可模拟复合材料中夹杂相形状和空间分布，已经成为一种求解复合材料等效力学性能的重要数值手段。郭然等[7-8]推导了考虑界面脱层的Voronoi单元有限元列式，对颗粒增强复合材料的损伤过程进行了模拟。郑宁昆[9]将时域自适应精细算法与VCFEM相结合，建立了含有夹杂相粘弹性单元的有限元递推格式。申柳雷[10-12]分别采用弹性VCFEM和不含夹杂相粘弹性VCFEM研究了推进剂细观特征参数与等效力学性能之间的影响关系。

本文将粘弹性本构模型在时域内进行离散，推导了含夹杂相粘弹性VCFEM有限元列式的递推形式。结合二分法计算了位移荷载下各时刻推进剂的松弛模量变化，并与ABAQUS对比验证了算法的正确性。运用该预示模型分析了推进剂粘弹性力学性能随细观特征参数的变化规律。

1 推进剂力学性能粘弹性VCFEM预示模型

1.1 Prony级数粘弹性本构模型的离散

如图1所示，广义Maxwell模型由多个Maxwell模型和一个弹簧原件并联组成，假设广义Maxwell模型两端受到应力荷载σ的作用，并定义第i个Maxwell单元的应力和应变分别为σi和εi，其弹簧原件的弹性系数为Ei，其粘壶元件的粘性系数为ηi。由于各Maxwell单元之间相互并联，因此每个单元具有相同的应变响应，而总应力σ等于各单元的应力之和。

对于第i个单个Maxwell单元，其应力应变关系满足：

(1)

对该微分方程，求解得

σi(t)=Yi(t)εi(t)

(2)

其中，Yi(t)即为松弛模量，写作

σi(t)=Eie-t/τiεi(t) (i=1,2,…,n)

(3)

其中，τi=ηi/Ei。

由于应力值ε相等，所以模型的总应变响应为

(4)

即

σ(t)=Y(t)ε(t)

(5)

其中，Y(t)即为广义Maxwell模型的松弛模量。

(6)

采用时域自适应算法[9]，得到第i个Maxwell单元应力应变关系在时间步ΔTk内的m阶展开式：

(7)

式中s为时间步ΔTk内一个无量纲的变量。

对于各向同性材料，将上式拓展到二维情形，得

(8)

其中

将式(8)中的m+1记作m，再根据s的阶次进行对应，整理可得

(9)

广义Maxwell模型应力应变关系在时间步ΔTk内的m阶展开式可写作

(10)

整理可得

(11)

其中

(12)

(13)

1.2 粘弹性VCFEM有限元列式

对于含有弹性夹杂相颗粒的单个Voronoi单元(见图2)，将各物理量在时域内进行展开，并根据s的阶次进行对应，可得到时间步ΔTk内的m阶展开递推格式：

(14)

对于含夹杂相的粘弹性Voronoi单元，其修正余能泛函在时间步ΔTk内的m阶的递推格式为

(15)

应力和位移m阶的递推格式写作

(16)

(17)

图2 基本Voronoi单元

将以上两式代入式(15)，整理可得

(βm)TDm+QTqm

(18)

其中

(19)

(20)

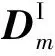
Hβm-Gqm+Dm=0

(21)

βm=H-1(Gqm-Dm)

(22)

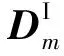
(23)

将βm向量代回到式(18)，有

(24)

其中

(25)

由余能最小原理和泛函的驻值条件，有

即

Kqm=-Rm+Q

(27)

将式(27)展开，写作

(28)

其中

(29)

同样，对每一个单元进行自由度凝聚和刚体位移抑制，得到

(30)

其中

累加每一阶的单元边界节点位移，即可得到每一个时刻的单元边界节点位移，进一步可得到每一个时刻的内部节点位移和各相的应力场结果。

2 粘弹性VCFEM算法

2.1 等效松弛模量计算方法

每一步时间步长的根据上一步的迭代步数m决定，当上一步迭代步数m小于步数阈值mlim时，则将时间步长扩大2倍。为了得到定位移下推进剂的等效松弛模量，引入二分法查找符合位移边界条件的节点荷载。为此，在每一个时间步的内循环基础上增加了一个查找的循环，该循环通过比较施加的力荷载得到的位移结果与给定的节点位移之间的比值，决定下一次节点力荷载的大小。如果某节点位移结果大于给定节点位移，则取节点力荷载与给定下限的1/2；反之，如果某节点位移结果小于给定节点位移，则取节点力荷载与给定上限的1/2。如此反复迭代，最终可得到节点位移符合要求的对应节点荷载，进而得到应力、应变场。采用文献[10]中的直接均匀化方法计算每一时刻的等效松弛模量。该计算方法的具体实施流程如图3所示。

图3 粘弹性VCFEM等效松弛模量计算流程图

2.2 粘弹性VCFEM预示模型正确性检验

为了验证粘弹性VCFEM算法的正确性，本节设计一个含30个颗粒的连续级配RVE模型作为验证模型。其中，颗粒直径为100～250 μm的等差数列，公差为10 μm，共有16级粒径分布，各级级配均有2个颗粒。RVE模型的尺寸为1200 μm×1200 μm，夹杂相的面积含量为56.1%，该模型的构造和网格划分均通过第二章所提方法实现，使用15 μm作为控制间距，颗粒空间分布见图4。

在模型顶部施加120 μm的位移荷载，模型下边界和左边界布置对称约束。基体相主曲线参考文献[5]中的Prony级数粘弹性模型，其松弛模量为

E(t)=0.244+0.275e-t/1000+0.21e-t/100+

0.23e-t/10+0.41e-tMPa

(31)

基体相泊松比νM=0.495。夹杂相：EI=32.4 GPa，νI=0.14。

如图5所示，VCFEM共划分为30个单元，ABAQUS共划分了30 879个四边形单元，包括14 989个基体单元和15 890个夹杂单元。

采用上文所述二分法计算材料的松弛模量，并与ABAQUS计算得到的结果进行对比(图6)，可发现两者得到的结果十分接近，相对误差在3%以内，达到了较高的精度要求。考虑到实际数值实现方法上的差异，本文并未对两者的CPU时间进行比较，但从每次迭代的刚度矩阵规模可看出，VCFEM具有明显的计算效率上的优势。

图4 多级配RVE模型

(a)VCFEM网格 (b)ABAQUS网格

图6 VCFEM和ABAQUS松弛模量结果对比

3 细观特征参数对推进剂力学性能影响分析

为了对推进剂粘弹性力学性能的影响进行深化分析，本节参考工程推进剂的常用配方，设计了三级配RVE模型作为分析模型(图7(a))，颗粒级配的粒径分别为80～120目(120～180 μm)、60～80目(180～250 μm)以及40～60目(250～425 μm)，颗粒之间的控制间距为5 μm。在模型顶部添加10 μm的位移均布荷载，约束模型左侧x方向的位移和模型底部y方向的位移。各级配的面积分数均为20%，故总面积分数为60%，换算为质量分数等于76.31%。

夹杂相为AP颗粒，其模量EI=32.4 GPa，泊松比νI=0.14。将HTPB作为基体相材料，泊松比取νM=0.495，为了确定HTPB的松弛模量，根据《GJB 770B—2005火药试验方法》等标准[13]，分别进行了-50、-30、23、50、70 ℃下的松弛试验，根据时温等效原理对试验结果进行处理，得到如图7(b)所示的23 ℃下基体的松弛模量主曲线，通过拟合得到Prony级数形式的松弛模量：

(32)

式中α=233.838 2，而各项系数如表1所示。

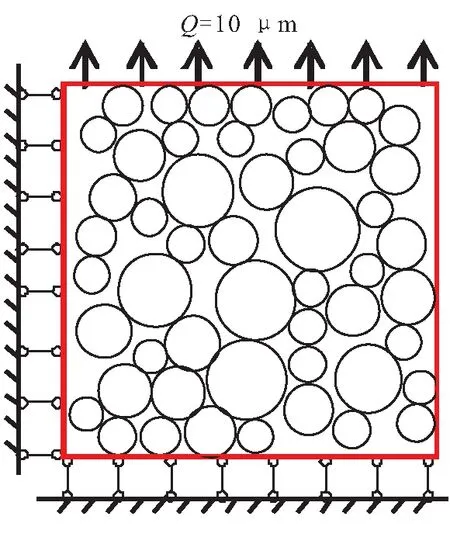
(a)连续三级配RVE模型

(b)基体相松弛模量23 ℃主曲线

表1 基体相松弛模量Prony级数系数

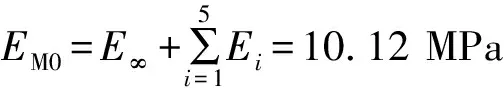
(33)

文献[1-2,5]均指出，在单轴应力作用下，颗粒的增强作用主要体现推进剂松弛模量的初始模量变化上，而反映模量随时域变化的α值变化较小。因此，本文采用等效初始模量和基体相初始模量的比值(即增强系数γeff)来表达颗粒的增强效应，相比于等效初始模量，γeff可更直观地体现出颗粒的增强效果。此时，推进剂的松弛模量可近似表示为

(34)

由于复合固体推进剂是由人工随机合成的，AP颗粒在推进剂中处于随机分布状态，而一个几何仿真模型只能反映一种分布状态，为了从统计学角度考虑几何仿真模型不确定性对结果的影响，运用顺序投放算法系统地构造了100个具有相同几何参数的RVE模型进行分析。

本节分析结果都将以含有误差条的曲线形式呈现，每一个点的纵坐标和误差条分别为所有样本结果的均值和标准偏差，这样的结果呈现方式可更好地表征结果的离散程度和不确定性。

3.1 基体相材料参数的影响分析

工程实践中，在不影响燃烧性能和能量特性的情况下，可通过添加不同剂量和不同种类的小组分添加剂，改变基体相的初始模量，这为推进剂的设计提供了调节参数；另外，作为粘弹性材料，由于温度效应，基体相材料在不同温度下面表现出不同的松弛模量。因此，有必要考察基体模量的改变对推进剂等效松弛模量的影响。本节固定其他细观参数，通过调整基体相初始模量EM0和泊松比νM，以分析基体相材料参数的影响，得到图8所示的曲线。

为了表达清晰，图8(a)选择3条松弛模量曲线进行分析。可看出，随着EM0的减小，推进剂的松弛模量随着时间依然保持S形的趋势，即由等效初始模量逐渐向等效平衡模量过渡，当EM0取值较小时(EM0=0.5 MPa)，初始模量和平衡模量非常接近，在不同EM0取值的曲线中，该曲线的变化趋势不是很明显。由图8(b)可知，随着EM0增大，推进剂的等效初始模量也呈线性增长，说明两者呈线性正相关关系。而不同基体相泊松比νM(分别取0.01、0.3和0.495)取值对推进剂等效模量的影响不大。

(a)不同基体相模量的松弛模量曲线

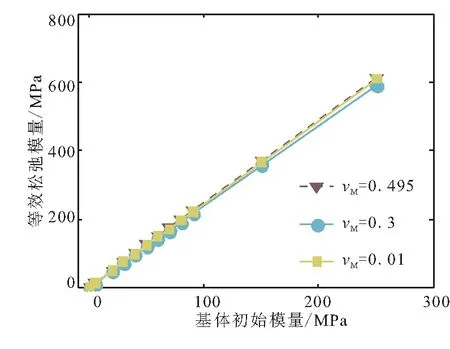
(b)等效初始模量

3.2 夹杂相材料参数的影响分析

本节计算不同夹杂相材料参数取值时的推进剂的松弛模量，得到图9所示的曲线。观察图9(a)可知，即使EI取值很小(10 MPa)，也可观察到推进剂的松弛过程，而随着EI增大，等效松弛模量基本相等；结合图9(b)可看出，当夹杂相模量大于2000 MPa时，等效初始模量的结果基本相等，验证了夹杂相模量变化可以忽略不计的结论。同时，由图9(b)还可发现，夹杂相泊松比νI的变化对推进剂的等效初始模量也没有明显的影响。在实际工程中，夹杂相模量EI远大于基体相初始模量EM0。所以，EI的变化不会对推进剂力学性能产生明显的影响。

3.3 细观结构参数的影响分析

夹杂相含量是推进剂主要细观特征参数，通过同步改变模型中各级配颗粒的数量，得到不同质量分数下的RVE模型。由图10(a)可知，随着质量分数的增加，推进剂的增强系数γeff呈现明显的增大趋势，且增长速度明显加快。由于随着质量分数的增加，推进剂等效模量加速增长，为了作图清晰，图10(a)的误差条的取值等于标准差与等效模量的比值。可看出，随着质量分数增大，增强系数的结果越离散。

(a)等效松弛模量随时间变化曲线

(b)等效初始模量

推进剂不仅是结构材料，更是一种燃烧剂，因而在设计中，颗粒含量常常根据能量特性的需要提前确定。因此，很多文献将研究重点转移到各级配的质量分布上。保持ψ1+ψ2=50.87%和ψ3=25.44%不变，增加第一级级配的质量分数ψ1，并相应减少第二级级配的质量分数ψ2，实现夹杂相级配质量分布的改变。如图10(b)所示，当ψ1取不同值时，增强系数γeff的变化幅度较小(<10%)。

保持颗粒质量分数76.31%不变时，改变第一级级配与第二级级配的粒径比例R1/R2，得到不同粒径比的RVE模型。通过计算，得到图10(c)所示的变化曲线。观察可知，粒径比变化对增强系数的影响并不是很明显。