数理结合的赛题典例
——第35届全国中学生物理竞赛预赛第6题的4种解法
2019-07-30钟云杰柏露枝
钟云杰 柏露枝
(江苏省常州市北郊高级中学,江苏 常州 213031)
填空题:田径场上某同学将一铅球以初速度v0抛出,该铅球抛出点的高度为H.铅球在田径场上的落点与铅球抛出点的最大水平距离为________,对应的抛射角θ为________.重力加速度为g.
1 命题意图研判
数学知识既是解决物理问题的工具,更是物理学发展的支撑和保障.应用数学知识解决物理问题的能力既是高考考查学生物理能力之一,也是全国中学生物理竞赛考查学生解决物理问题能力水平的重要内容之一.第35届全国中学生物理竞赛预赛第6题的解法中,蕴含着丰富的数学思想和方法,因此,该题的命题意图旨在通过求斜上抛运动的最大水平射程,凸显中学生应用数学知识解决物理问题的能力水平.现由该题的四种解法展示命题本意.
2 4种解题方法
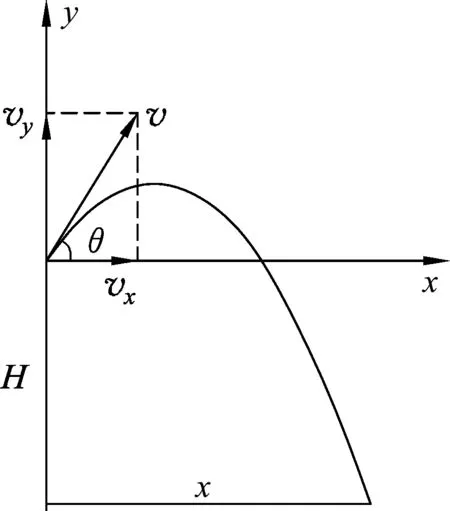
图1
方法1:分解速度法.
抛体运动常规的处理方法是,将运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动,如图1所示.由匀速直线运动和竖直上抛运动规律得
vx=v0cosθ.
(1)
vy=v0sinθ.
(2)
x=vxt.
(3)
(4)
由(1)-(4)式可得
(5)
(5)式可化为
(6)
显然(6)式是以tanθ为参数的一元二次方程,因为θ有解,
所以Δ≥0,即
由此解得

解法认知:解决抛体运动问题,通常是将抛体运动分解为水平方向和竖直方向两个分运动来处理.虽然方法1是一种常规的分解速度法解抛体运动问题,但对学生的数学方程知识、三角函数知识的应用能力有一定的要求.
方法2:分解加速度法.
将加速度分解为与速度方向共线(反向)以及与速度方向垂直两个方向,如图2所示.由图2可知,物体在初速度方向做匀减速直线运动,在垂直初速度方向做初速度为0的匀加速直线运动.
由图3可见,当物体沿初速度方向速度减为0时,物体沿初速度方向位移达到最大(Q1位置),此时物体到达地面的实际位置达到最远,即Q位置,BQ长度即为所要求的最大射程xm;图3中∠BAO等于所要求的对应抛射角θ.

图2
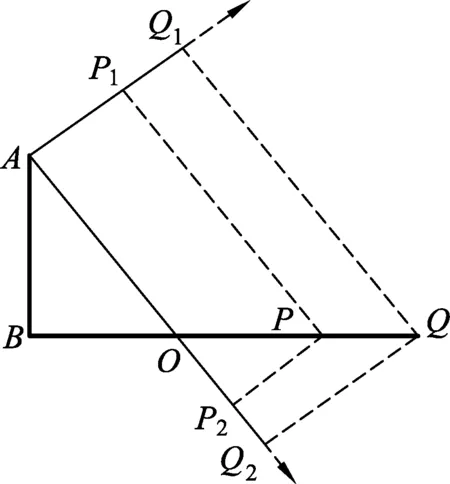
图3
由加速度分解可得
g0=gsinθ.
(1)
v0方向的最大位移为
(2)
由几何关系可知∠BAO=∠Q2QO,故有
(3)
有(1)-(3)式可得
(4)
(4)式由基本不等式规律可知
即
(5)
将式(5)代入式(4)得
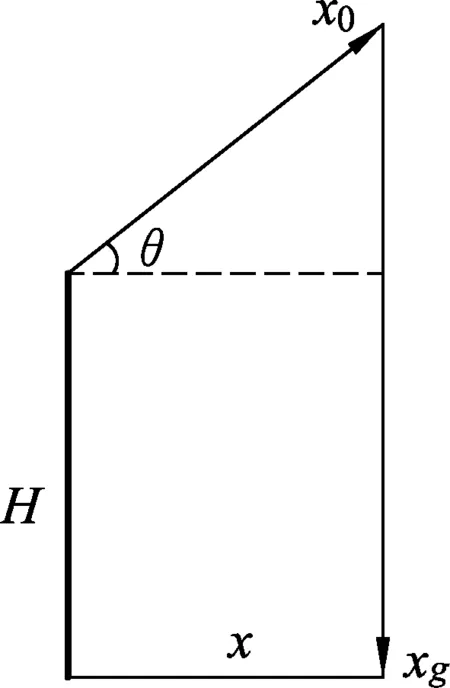
图4
解法认知:运动的分解具有多向性.分解加速度求解抛体运动问题比分解速度求解抛体运动问题在思想层面上突破常规.但分解加速度这种求解方法,对学生几何知识和不等式知识的应用能力有一定的要求.
方法3:自然分解法.
将物体的运动分解为沿初速度方向的匀速直线运动和竖直方向的自由落体运动,如图4所示.由此得:
在初速度方向有
x0=v0t.
(1)
在竖直方向有
(2)
由几何关系可得
(3)
由式(1)-(3)可得
(4)
(4)式中,将t2作为自变量,可知

(5)

(6)
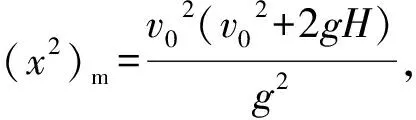
(7)
将式(6)代入式(1)可知
(8)
由于抛射角θ和x0、xm的关系满足:
(9)
所以由式(7)-(9)可知

解法认知:自然是一种状态,解题的自然性、本属性是思维的基本出发点.基于运动的自然性,抛体运动是初速度方向和竖直方向两种运动的合运动也就顺以为然.显然从初速度方向的匀速直线运动和竖直方向的自由落体运动求解此题不失为一种基本的、自然的求解方法,但这种解法中凸显出对一元二次方程和二次函数知识的灵活应用水平.
方法4:动能定理法.
由解法1的图1可知
vx=v0cosθ.
(1)
x=vxt.
(2)
由式(1)、(2)可得
x=v0tcosθ.
(3)
由于初速度v0确定,即初动能确定;高度也确定,由动能定理可知,末动能确定,即末速度v的大小为定值.那么,由动能定理有
(4)

图5
末速度矢量分解如图5,易发现速度矢量三角形面积为
(5)
由式(3)、(5)可得
(6)
而矢量三角形面积又满足
(7)
由式(6)、(7)可知
(8)
要使x有最大值,则θ+α=90°,结合(4)后应有
抛射角满足
(9)
由式(4)、(9)可知
解法认知:物理知识是解决物理问题之本.动能定理法求解此题,将功能思想融合在纯运动问题的解题之中,突破了解决纯运动问题的求解域界,实现了思维跃迁.但动能定理法求解此题对学生向量知识、几何知识和三角函数知识的灵活应用能力有较高的要求.
综上可见,该题的4种解法,以运动的合成与分解为主体,以数学知识的综合应用为主知,以学生的数理结合能力为主导.总之,在这4种解法中,既体现了解决物理问题的自然美和创新美,又体现了物理美和数学美在解决物理问题中的结合美.
