高中生物理模型思维的分层测试研究
——基于SOLO分类评价理论和哥特曼量表法
2019-07-30朱宁波
袁 媛 朱宁波
(辽宁师范大学教育学院,辽宁 大连 116029)
1 问题的提出
我国《普通高中物理课程标准(2017年版)》(以下简称“2017版高中物理课标”)将“模型建构”能力作为学科核心素养的重要内容,归入科学思维素养指标之中.本课题组在前期研究中,揭示了物理建模能力由“非认知能力”、“基础能力”和“专项能力”3个维度下的11个要素指标构成.[1]其中,“专项能力”维度下的“模型思维”是形成和发展学生物理建模能力的核心要件.教学设计原理明确指出教学设计始于对学生已有能力发展水平的认知和定位,因而,要通过物理教学培养学生的建模能力,同样要先准确地评定学生现有能力水平,定位学生的能力发展阶段,找到合适的发展路径,实现学生能力发展的进阶.然而,物理建模能力相对知识而言,处于“软”状态,难以直观、定量地测量和评价.本研究基于SOLO分类理论,建构了物理模型思维能力的层级,并在此基础上依托SOLO开放试卷设计理念编制了一套符合高中生认知发展水平的物理模型思维试题,并利用哥特曼量表分析法对试题质量进行检验.该研究将在一定程度上,帮助我国教育者准确测量和定位高中生物理建模能力水平,从而为有效地选择培养策略和设计培养方案提供参考和依据.
2 核心概念的内涵界定
“物理建模能力”是个体具备一定的物理建模意识,并能从实际问题中抽取核心要素及要素间的关系,进而构建物理模型来解释和预测现象的个性心理品质.物理建模能力是一个非智力因素和智力因素相统一的智能系统,它既包括在科学实践中发挥原动力和惯性作用的“非认知因素”,还包括个体参与各种科学实践所应具备的共同的“基础能力”,以及指向物理建模实践的“专项能力”.其中,专项能力维度下的“模型思维”要素是物理建模能力的核心要件.
“模型思维”是指个体从原始问题情境中抽取核心要素,将原始问题转化成物理问题,并建立要素间清晰的建模路径的能力.它是最能体现物理建模能力不同于其他学科建模能力独特性的关键品质.
“SOLO试题”是一种基于SOLO分类理论,对学生的开放式反应做出成绩评定的测量工具.[2]它运用SOLO分类法的基本思想,将一个原始开放性问题按照人的思维水平从低到高的难度,编制成对应SOLO单点结构、多点结构、关联结构和拓展抽象结构4个层次的开放性子问题,这4个子问题构成一道完整的SOLO试题,进而通过观察学生对4个子问题的反应样式来评定学生思维的发展水平.
3 物理模型思维能力的层级系统
模型思维的过程非常复杂,包括许多组织和连结,需经历从“无结构”到“有结构”的历程,因而难以通过传统试题进行观察和测量.SOLO分类理论认为通过学习结果在结构上的复杂程度的变化可以实现对学生认知结构或学习质量的层次评定.在大量研究数据支撑下,Chan与 Tsui等学者认为比格斯的SOLO分类理论对区分如模型思维这样复杂的认知能力最有效.[3]所以,本文借鉴SOLO对个体思维结构从低到高划分为前结构、单点结构、多点结构、关联结构和拓展抽象结构的理论,构建物理模型思维能力的层级模型.
科学哲学家亨普尔认为,人们必须依靠“科学理论”才能系统、精确、深入地理解自然现象和过程.[4]继而,亨普尔又通过“空中之网”的隐喻揭示了科学理论的理解过程——科学理论的空中之网漂浮在人们经验观察的平面之上,只有经验观察面上的某点以某种“合理的解释规则”与科学理论网络中的相应节点建立连接,人们才能实现对科学理论的理解.金得浦、林定夷等学者认为,在经验观察面和空中之网间存在的所谓“合理的解释规则”即是科学模型,人们只有取得了关于模型的知识,才能认识自然现象,理解科学理论,模型起着桥接的作用.[5-6]由此,本文认为模型思维能力的层次划分应主要考虑界于经验反应和科学理论之间的水平,即经验反应和科学理论两个阶段外在于模型思维能力水平.物理模型思维能力层次划分如表1所示.

表1 物理模型思维能力的层级
4 物理模型思维能力试题(PMTT)的编制和质量检验
4.1 PMTT的设计和编制
2017版高中物理课标在“考试命题建议”中,要求“试卷评分标准应清晰准确,要摒弃单纯的、知识性的描述方式,要研制基于核心素养的等级”.[7]物理模型思维能力试题(Physics Model Thinking Test,简称PMTT)的编制恰逢其时,它既满足了基础教育评价模式转变的这一要求,又实现了“客观、全面、有效地收集学生物理学科核心素养发展水平的信息,真实反映学生物理学科核心素养发展的水平”[7]的评价目标.
PMTT的设计核心是将原始开放性问题改编成符合SOLO的单点结构、多点结构、关联结构和拓展抽象结构的4个子问题.由此可知,保障PMTT质量的关键是编制出与模型思维各层级精准对应的子问题.通常编制子问题的路径有两条:一是试题编制者预估学生可能做出的各种反应,依此设计子问题.这样做可以避免预测试带来的工作量,但预估反应与学生真实反应间存在较大差异,必将影响试题的信效度.本研究则采取第二种路径,即通过小范围预测试,获得学生的典型答案,以此作为设计不同层级子问题的依据.该路径能较好地保证试题的质量,但它要求预测试的被试必须囊括各层级的目标对象,否则将导致收集不到单点结构水平或拓展抽象水平的相关信息,给问题设计带来困难.
在与物理任课教师充分沟通之后,笔者有针对性地选择了来自5所高中的物理建模能力水平存在差异的30名同级学生,向他们提供原始开放性问题.测试后,笔者按照模型思维层级(见表1)将学生答案分层,并提炼各层级的典型反应,以此作为子问题的设计依据,最终将原始开放性问题改编成PMTT试题.如我们将原始开放性问题“跳绳是一项非常好的健身运动,它不仅能让全身肌肉匀称有力,还能让人的呼吸系统、心脏、心血管系统得到充分的锻炼.设某运动员的质量是50 kg,他1 min跳绳180次.假定在每次跳跃中,脚与地面的接触时间占跳跃一次所需时间的2/5.请问运动员重力做功的平均功率是多少?”经过预测试,分析学生各层级的典型反应后,设计出的4个子问题分别为:(1) 请你运用物理学知识,说一说运动员的脚离开地面腾空过程中,所做的是什么运动?(2) 你能说出运动员跳绳过程中,克服重力做功应考虑什么因素吗?(3) 请你说明运动员从起跳到跳到最高点的过程中,机械能的转化与重力做功间的关系.(4) 请你将运动员跳绳过程中,运动员所受重力、脚离开地面的时间、腾空时间、从起跳到最高点的位移等因素综合起来,解释运动员跳绳时克服重力做功的平均功率.这4个子问题按照模型思维能力水平1到水平4的顺序排列,后一题是前一题的延伸和拓展,要回答后一题,就必须具备回答前一题的相关知识与能力.如果学生能够正确回答第一个子问题而无法回答后面3个子问题,则表明学生模型思维能力达到了水平1的水平,得1分;如果学生能够正确回答前两个子问题,得2分;以此类推.
4.2 PMTT质量检验
设计和编制PMTT,只是实现了测评学生模型思维的第一步,要使试题运用于大规模的评价,试题质量检验必不可少.目前,哥特曼量表分析法被认为是检测SOLO试题质量的有效方法.哥特曼量表是一种具有累计特征的态度量表,通常情况下,它包含某人对某个特定对象所持态度的一组陈述.哥特曼量表按照陈述肯定程度逐步加强的顺序排列,其逻辑起点是假设当某人赞同某个陈述,就一定会赞同低于该肯定程度的其他陈述.哥特曼量表结构与SOLO试题具有一致性,因此可以借鉴哥特曼量表分析法检验PMTT的质量.
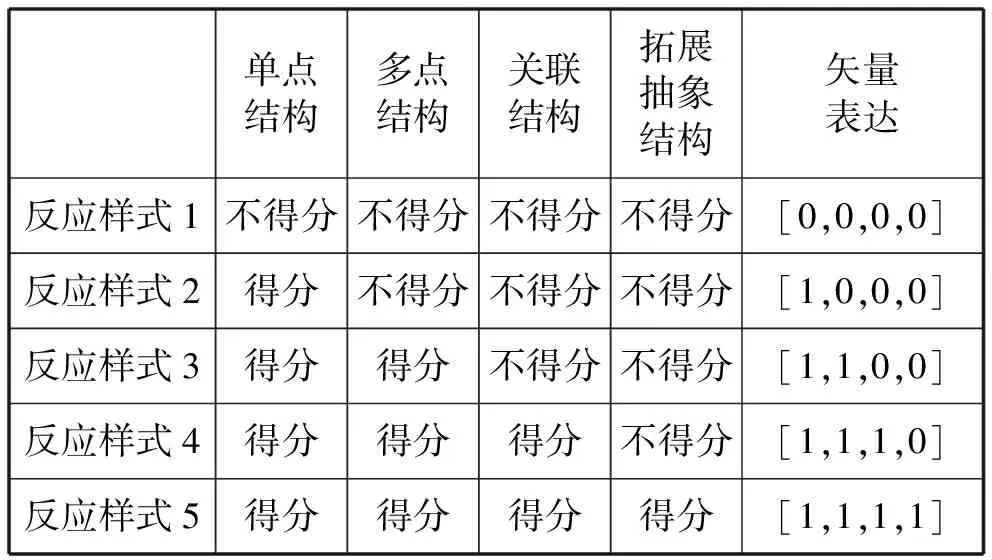
表2 SOLO试题的反应样式
表2中所列出的反应样式被称为“常态样式”,而与此样式不符的则被称为“反常态样式”,如[1,0,1,0].在哥特曼量表分析法中以“再现系数”(coefficient of reproducibility,简称rep)作为判定SOLO试题质量的指标,再现系数越大表明试题质量越高,rep可表示为
在上式中,总反应次数等于反应样式数目(SOLO类试题反应样式数目为5)乘以被试总人数,总误差次数等于“反常态样式”出现的总次数.当rep≥0.95时,该试题被认为是完美哥特曼量表.当rep≤0.90时,则需要分析原因.导致这一情况的原因有二:一是试题编制问题.如出现“反常态样式”[1,0,1,0],则可能是代表关联结构的子问题难度低于代表多点结构的子问题;二是学生心理、生理或环境等因素影响造成的反应误差.假设是第二种原因导致rep≤0.90,可以做一个近似处理,即将与其反应样式最为接近的“常态样式”[1,1,1,0]作为该被试的反应样式的测试结果.但如果“反常态样式”出现率很高,则要从试题本身的质量去找原因.
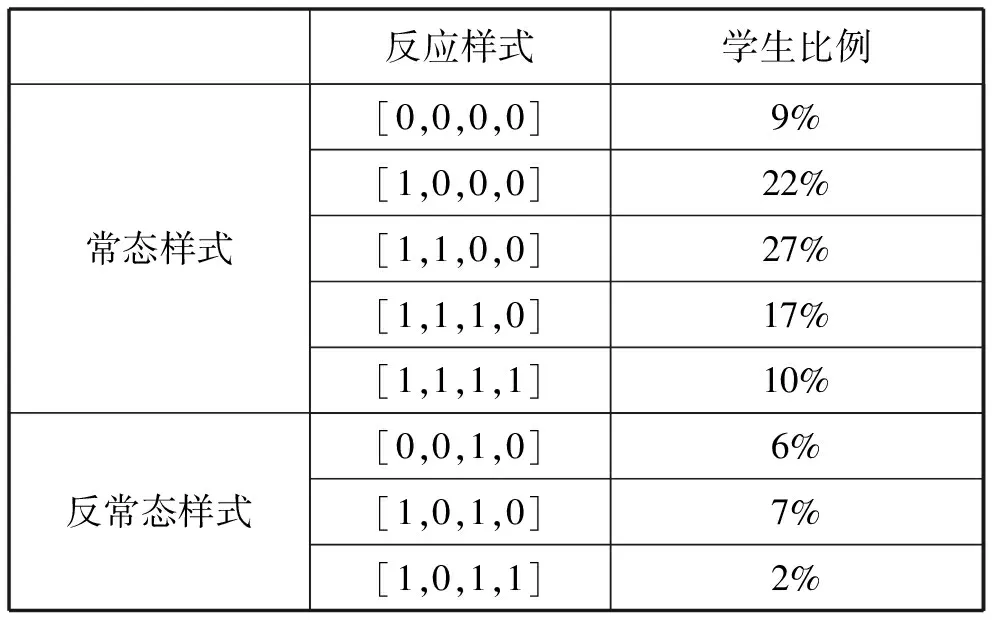
表3 学生对“跳绳问题”做出的反应样式

5 研究结论
PMTT与原始开放性试题相比,在评定学生模型思维能力的信度方面有很大提升.首先,它解决了评分标准难以统一的问题.原始开放性问题没有固定的结论,学生的答案五花八门,再加上评分者的主观性,最终导致不同评分者对同一个学生的回答会给出差异较大的分值,难以保障评分的信度.PMTT则是将一个大的原始问题分解成四个不同等级的子问题,从而在一定程度上约束了评分者对学生评定的“自由度”,缩小不同评分者对同一反应给出评分的差异,提高评分信度.其次,用PMTT测量和评价学生模型思维能力的科学性强.PMTT是基于标准参考方式划分等级的基础上设计试题和评价学生的,即根据一套外在客观的能力标准,独立地判断学生达到标准的程度,它比常模参照等级划分方式具有明显优势,例如,不同批次的测试具有可比性、等值性,测试成绩只与学生自己的能力水平有关,而与其他考生的水平无关.这在很大程度上保障了测量和评价的公平性.
总之,在近年来高考制度改革背景下,试卷评分标准强调摒弃单纯的知识性的描述方式,重视研制基于核心素养的等级评价,那么,PMTT这样的SOLO试题必将成为传统试题的有益补充和未来学业水平考试的发展趋势.
