样本加权的多视图聚类算法

洪 敏 贾彩燕 李亚芳 于 剑

1(交通数据分析与挖掘北京市重点实验室(北京交通大学) 北京 100044)

飞速发展的信息技术使现实世界中的数据不仅呈现出规模庞大的特性，而且多源信息采集技术和多样化的特征表示使得多视图数据在众多实际应用中越来越普遍.例如Web网页可以从3个不同的角度描述：词向量视图直观刻画了网页文本中单词的出现情况；网页中的图像提供了丰富的视觉特征视图；网页与网页之间的链接关系展示了网页内容彼此之间的相关性.多视图数据的互补性和一致性有利于从不同方位协同完成特定的机器学习任务.因此，多视图学习逐渐受到人们的关注.

多视图研究最早起源于Yarowsky[1]和Blum等人[2]提出的消除单词歧义算法和协同训练算法.Yarowsky[1]将文档中单词信息和单词所在文档信息定义为2个视图，并将不同视图加入各自的分类器进行交互学习.Blum等人[2]在对多视图定义分类器的同时，基于视图独立性的原则引入协同训练.Bickel等人[3]以协同EM(expectation maximiza-tion)算法为基础，提出了多视图EM和两视图球状K-means算法.Cleuziou等人[4]提出了CoFKM(centralized method for multiple-view clustering)算法，通过集中式策略使多个视图的信息尽可能的一致.Sa[5]构造了一个二视图谱聚类算法，创建一个描述2个视图共现信息的二部图，以最小化视图之间的不一致性.Kumar等人[6-7]相继提出了在多视图谱聚类加入协同训练和协同正则的方法，保持了不同视图上聚类结果的一致性.

但是，上述方法平等看待各个视图，难以体现不同视图信息对簇结构重要性的差异，因此出现了一些视图权重学习的经典算法.较早的工作是Tzortzis等人[8]给出的多视图带权凸混合模型(convex mixture models, CMM).该模型对不同视图训练相应的CMM模型，同时为各个视图分配自适应权重，并将自学习视图权重思想推广至核K-means，设计了多视图核函数K-means算法(multi-view kernelK-means, MVKKM)[9].该算法通过预先定义的核函数将原始数据映射到新的特征空间，并根据视图对簇划分结果的贡献度为每一个视图分配权重.为了适用大规模多视图数据，Cai等人[10]给出了RMKMC模型，不仅在目标函数中新增视图权值参数，同时2,1范式还增强了算法的鲁棒性.最近，Nie等人[11-12]从图的角度提出了2种适用聚类和半监督分类的多视图学习模型：AMGL和MLAN.AMGL[11]凭借视图近邻图学习，构建出了多视图谱聚类权重学习框架;MLAN[12]通过学习多图局部流形结构，不断修正簇结构矩阵以优化聚类性能.

多视图学习不仅是不同视图之间的有效性融合，而且视图特征的选择也是多视图学习的重要组成部分.Chen等人[13]提出了自适应双权多视图算法(TW-K-means).该算法能同时学习视图权重和特征权重对簇结构的贡献.Xu等人[14]提出了具有特征选择的加权多视图聚类算法(weighted multi-view clustering with feature selection, WMCFS).Zhang等人[15]在多视图权重学习模型中增加了视图间的一致性约束，设计了性能良好的TW-Co-K-means模型.

除了以上的学习不同视图和特征对簇结构贡献差异的“全局”模型外，Li等人以节点属性和节点的链接关系为2种数据源，学习了不同样本点上不同类型信息对社区结构(即簇结构)贡献的“局部”差异[16]，给出了Adapt-SA模型，取得了不错的效果.但该模型需要对2种信息下的数据进行同维变换，不但缺乏灵活性且同维变换易造成原有数据上信息的损失.因此，我们基于两视图同维变换样本局部权值学习模型Adapt-SA，提出了一种新的多视图样本加权聚类算法(sample-weighted multi-view clustering, SWMVC).该算法不仅可以学习不同样本点对多个视图间权重的差异，具有“局部”学习能力，而且还可以从“全局”角度反映不同视图对簇结构的贡献差异.另外，该方法不仅克服了Adapt-SA方法同维变换的约束，而且将Adapt-SA的思想从2个视图扩展到多个视图上.

1 相关算法介绍

1.1 MVKKM

MVKKM(multi-view clustering kernelK-means)[9]是一种基于核函数的多视图权值模型.相比传统的视图权值方法，该算法使用事先定义的核函数对数据进行映射，然后在多视图K-means中学习各个视图的重要性.其目标函数:

(1)

1.2 WMCFS

基于MVKKM思想，WMCFS(weighted multi-view clustering with feature selection)[14]模型在多视图K-means聚类过程中同时考虑不同视图和各个特征的差异，设计了目标函数:

(2)

其中，ωv和τv分别表示视图权重和视图中各个特征的权重，p和β是分别控制视图和特征稀疏性的参数.

1.3 TW-Co-K-means

TW-Co-K-means(two-level weighted collaborativeK-means)[15]采用协同策略约束不同视图之间的一致性，进而学习视图和特征对簇结构的重要性.其目标函数:

(3)

(4)

(5)

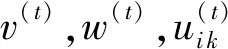
1.4 Adapt-SA

Adapt-SA(adaptive fusion of structural and attribute information)[16]是面向图聚类问题提出的一种学习样本上不同种类信息(链接信息和节点属性)对节点簇结构重要性差异的K-means型算法.该算法首先将2类信息映射到同维空间上，再进行加权融合.因此，融合后的表示具有统一的簇中心.其目标函数:

(6)

2 基于样本加权的多视图聚类算法

Adapt-SA虽然可以学习不同样本间2类信息重要性的差异，但该方法在进行信息融合时，需要对原空间数据进行同维变换，可能会造成一定的信息损失.并且，同维变化也会带来算法复杂性的增加.在实际应用中，可能某个视图的维度适当，最宜在原空间进行簇结构学习，使得Adapt-SA缺乏灵活性.因此，本部分我们给出了一种普适性更强且能够学习不同样本点权值的多视图K-means算法，以弥补Adapt-SA算法的不足.

2.1 基本定义

为方便介绍所提出的算法模型，本节所用符号的具体含义如表1所示：

Table 1 The Symbol Meaning表1 符号含义

2.2 SWMVC算法

受Adapt-SA思想的启发，并结合多视图K-means算法，为了描述多视图聚类过程中每个样本点的不同视图对簇结构的贡献，SWMVC算法优化模型:

(7)

因此，SWMVC模型具备3方面的特点：1)能使每一个视图拥有独立的簇中心；2)每个样本点对多个视图拥有自己对簇结构贡献的权重影响，具有局部学习能力，同时通过样本点在各视图上的不同重要程度，易于统计各视图对簇结构的全局重要性；3)不但可以在多个视图的原空间进行操作，也可以在变换后的视图空间(如使用Adapt-SA模型中的同维变换策略)进行学习，灵活性高.

2.3 SWMVC模型求解

在求解时，针对每一个类寻求所有视图到每个类中心的带权距离最小值.即按照式(8)进行计算，之后根据得到的最小值结果对每个数据点进行指派.

(8)

(9)

(10)

(11)

(12)

根据上述模型求解过程知，本节构建的基于样本加权的多视图聚类算法(SWMVC)的详细步骤如算法1所示：

算法1.SWMVC.

输入：多视图数据集X={X1,X2,…,XV}、类个数K、参数λ、最大迭代次数tmax;

输出：X的共有隶属度δ、样本权集αv.

② 根据式(8)更新δ；

⑤t=t+1；

⑥ 如果t>tmax，停止算法，返回δ和αv.

3 实验设计与结果分析

3.1 数据集描述

为了评估本文提出的基于样本加权的多视图聚类模型(SWMVC)算法的效果，对不同的多视图权值聚类模型进行实验和对比分析.我们选取了视图之间是异质特性的6个数据集，分别是WebKB中的Cornell,Texas,Washington,Wisconsin网络/文本数据集和图像/文本数据集Wiki和VOC以及视图具有同质特性的2个数据集：Handwritten numerals和Caltech101-7.

1) WebKB数据集

Cornell,Texas,Washington和Wisconsin是WebKB网页数据集的子集，分别包含195,187,230,265个样本.每个样本通过引用关系视图和文本内容属性视图进行描述，对应的成对视图维数分别是195维和1 703维、187维和1 703维、230维和1 703维、265维和1 626维.该数据集涉及到5个类别课程、学院、学生、工程和员工.

2) Wiki数据集

Wiki是从维基百科专题文章中提取的数据集，常用于跨模态检索中.该数据集由2 173个训练样本和693个测试样本组成的图片-文本对数据，共有10个类.其中，每一张图片使用128维SIFT特征向量视图表示，并含有相关图片的10维文本LDA主题描述向量视图.

3) Pascal Visual Object Classes 2007数据集

Pascal Visual Object Classes 2007(VOC)是一个自然图像数据集.选用其中的2 808张图片,每一张图像有512维的GIST特征和399维的TF-IDF(term frequency-inverse document frequency)文本特征.涉及到20个类aeroplane,bicycle,bird,boat,bottle,bus,car,cat,chair,cow,dining table,dog,horse,motorbike,person,potted plant,sheep,sofa,train,tv/monitor.

4) Handwritten numerals数据集

Handwritten numerals(HW)是一个含有10个类的2 000个手写体数字数据集.本实验选取其中的5个视图数据，分别是维数76维FOU特征、216维FAC特征、64维KAR特征、240维PIX特征和47维ZER特征.

5) Caltech101-7数据集

Caltech101-7是一个对象识别数据集.包括1 474张图片，被划分为7个类，分别是Face,Motorbike,DollaBill,Garfield,Snoopy,Stop-Sign,Windsor-Chair，含有图像的Gabor,Wavelet,CENTRIST,HOG,GIST和LBP 6个特征，并将其作为Caltech101-7的6个视图，对应视图的特征维数分别为48维、40维、254维、1984维、512维和928维.

3.2 实验方案

为了全面评估本文提出的基于样本加权的多视图聚类模型的性能，在实验部分中对比研究了多视图聚类领域中的多个代表性算法：

1) WMCFS[14]是一种具有特征选择功能的多视图聚类算法.该方法的2个参数p和β利用网格贪心搜索方法在3.1节介绍的8个数据集上依次设置为{5,0.5}，{30,0.0005}，{20,0.5}，{30,0.0002}，{10,0.5}，{20,0.0005}，{10,0.1}和{5,0.0005}.

2) MLAN[12]是一种面向图聚类的多视图聚类算法.与传统图聚类不同的是，它考虑局部流形结构在每一轮迭代不断修改相似性矩阵，直至获得最优矩阵.该方法可以自动学习各个视图的权重系数.其隐含参数近邻数k=9.

3) AMGL[11]该方法假设所有图共享潜在簇结构，是一种无参数的多图学习框架，即在学习时能够为各个图分配合适的权值，可以应用于多视图聚类和半监督分类任务.其隐含参数近邻数k=5.

4) TW-Co-K-means[15]是一种融合视图和特征的多视图算法.该方法全面考虑不同视图的互补性和一致性，以协同方式挖掘不同视图间的共享信息，同时考量了每个视图的多样性特点.参数η，α和β在各个数据集分别采用网格贪心搜索方法设置为{0.8,10,60}，{0.8,30,60}，{0.1,20,80}，{0.9,50,80}，{0.3,30,8}，{0.01,80,50}，{0.6,10,50}和{0.2,30,8}.

5) SWMVC是本文提出的基于样本加权的多视图聚类算法.模型中含有样本权稀疏系数，参数λ经过网格贪心搜索方法在各数据集的值分别设为100,75,35,60,0.5,1,10,45.

3.3 实验结果分析

本节首先展示不同方法在各种多视图数据集上的聚类效果，然后展示WebKB,Wiki和VOC所有样本在给定视图的权重分布，最后研究了参数λ的敏感性.

1) 多视图聚类效果对比

表2～4分别展示了各多视图聚类方法在8个数据集上的聚类评价指标ACC，NMI和F-measure.其中，各个算法精度选用20次运行结束的最大值，各多视图聚类算法在同一数据集上的最好结果用黑体表示.

由表2～4可以看出：

① 相比传统多视图聚类方法，本文提出的基于样本加权的多视图聚类算法(SWMVC)在Cornell，Texas，Washington，Wisconsin，Wiki和VOC数据集上有较好的性能提升.具体来说，SWMVC的ACC和F-meansure指标值比传统的多视图聚类算法TW-Co-K-means在前5个数据上分别提高了约0.03和0.02，在VOC上取得了次优结果.在NMI指标上，SWMVC在异质数据Texas,Washington,Wisconsin和VOC获得了最高结果，在Cornell和Wiki以0.208 2和0.538 8取得了第2高结果.究其原因，我们发现：WebKB的4个数据集由链接结构视图和文本内容视图2种异构视图描述，能够形成较强的互补关系；Wiki和VOC由图像特征视图和文本特征视图2种异构视图组成，同样具有较好的互补性，且文本特征视图解释力强于图像特征描述子.

② SWMVC在手写数据集HW和图像数据集Caltech101-7表现欠佳，原因在于尽管这2个数据集的多个视图从各个方面进行了描述，但是视图之间表现出同质特性，视图间的信息互补性相对较弱，且对簇结构的刻画能力在局部样本上的差异性不明显.

Note: The best results are highlighted in bold.

Table 3 NMI of Different Clustering Algorithms on Multi-View Datasets表3 不同聚类算法在多视图数据集上的NMI值

Note: The best results are highlighted in bold.

Table 4 F-measure of Different Clustering Algorithms on Multi-View Datasets表4 不同聚类算法在多视图数据集上的F值

Note: The best results are highlighted in bold.

Fig. 1 Weights of samples in a given view图1 各个样本在给定视图上的权重

③ 根据实验结果可以发现：MLAN模型在HW和Caltech101-7效果显著.究其原因，MLAN学习了数据的局部流形结构，多个同质视图上局部流形结构的整合较好地反映出了全局的簇结构信息，是目前较为突出的模型.

④ 综合WMCFS和TW-Co-K-means多视图特征算法在上述8个数据集的实验结果可见：良好的特征选择机制可以提高多视图聚类算法的性能.

2) 节点权重分析

为了进一步验证本文提出的SWMVC算法，我们在图1中展示了该方法在6个异构视图数据集Cornell,Texas,Washington,Wisconsin,Wiki和VOC上学习到的样本权重.其中，横坐标表示样本编号，纵坐标表示各样本在WebKB四个数据链接视图上的权重及Wiki,VOC数据集的各样本点在文本视图上的权重.

由图1可以看出：整体上WebKB四个数据集的样本在链接视图所占权重较大，即拓扑结构更能刻画数据特性；Wiki和VOC各样本点在文本视图权重大于图像特征视图.同时视图包含重要度样本越多，说明该视图该视图越重要，实现了对数据“全局”信息重要性的学习.

对于同质的多视图数据集HW和Caltech101-7，SWMVC算法学习到的各样本点的权重差异性小.由于这2个数据集视图多，考虑到空间限制，只简单描述如下：HW数据集所有样本在FAC,FOU,KAR和ZER视图权重基本分布在0.21左右，在PIX特征视图权值约为0.16；Caltech101-7所有样本点在前3个视图权重约为0.20，第4个视图权值约是0.06，最后2个权值为0.17左右.从而进一步可见，我们的方法更适于差异性较大的异构互补视图的簇结构学习问题.

3.3 参数敏感性分析

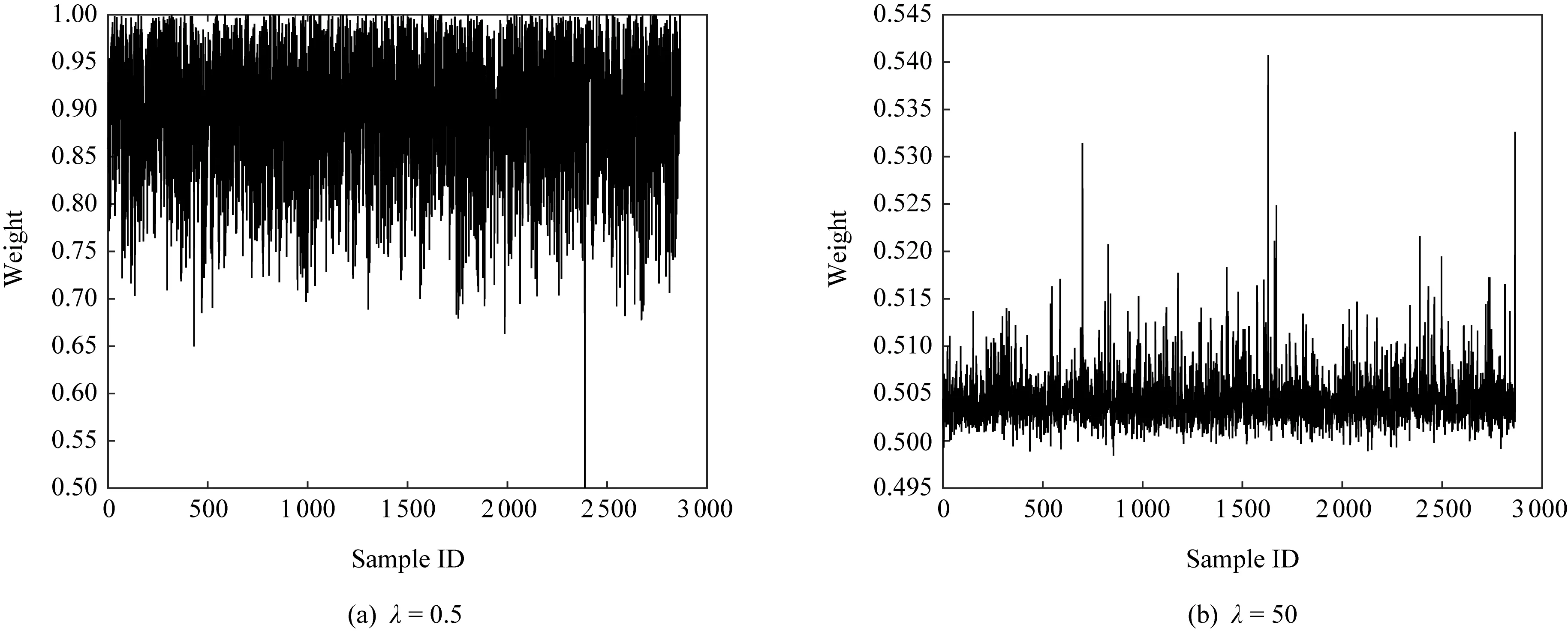
Fig. 2 The influence of λ on sample weights图2 参数λ对样本权重分布的影响

4 总 结

本文主要提出了一种基于样本加权的多视图聚类算法(SWMVC).为了更好地学习多视图蕴含的信息，本文受Adapt-SA算法启发，引进多视图学习思想，从不同视图角度学习样本对簇结构的贡献度.这种多视图样本加权学习机制不仅体现了样本差异性，而且还刻画了视图的重要度，实现了对数据“局部”和“全局”性质的学习.与此同时，SWMVC能够保留数据原始信息，有助于降低模型复杂度.在6个异质视图数据集和2个同质视图数据集上的大量实验对比表明：本文提出的模型在异质视图数据上具有不错的聚类效果.