电磁发射弹丸飞行弹道仿真*

李湘平，鲁军勇，冯军红，李 开，杜佩佩

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

电磁发射一体化弹丸弹道是指弹丸从出炮口开始，至到达目标产生攻击效果的全过程，它直接影响武器系统作战性能。因此，需要深入研究其在大空域、宽速域下的飞行弹道特性，为其作战使命任务分析提供依据。有关电磁发射高超声速一体化弹丸的飞行弹道研究，国内外研究的重点主要集中在弹道仿真、弹丸结构以及气动加热等方面，着重考虑在超高速条件下弹丸在空气中飞行高度和射程、摩擦烧蚀等一系列问题。

Satapathy和McNab等根据8 MJ电磁发射弹丸的实际外形尺寸建立了相应的计算流体力学(Computational Fluid Dynamics，CFD)模型，并利用此模型解算获取不同马赫数条件下的气动参数[1]。法德实验室(Institute of Saint-Louis，ISL)的Hundertmark等建立了电磁发射弹丸弹道模型，并结合气动以及气动加热模型，考虑5 kg弹丸在发射角度从2°到80°各情况下的飞行轨迹，并分析得到了不同发射角度下弹丸表面的温度情况，仿真结果表明5 kg弹丸最大射程可以达到500 km，最大飞行高度可以达到260 km[2]。洛克希德·马丁公司的Skurdal等构想了一种多用途的电磁发射装置，这种发射装置可支持战术武器的多次发射，并比较了不同发射武器条件下弹道轨迹的特点[3]。

尚晓兵[4]根据电磁发射弹丸在弹道飞行的特点，建立了弹丸刚体六自由度模型，考虑在具体弹道参数条件下，利用相应的仿真模型对电磁发射弹丸弹道进行仿真，但其未考虑环境因素以及弹体热烧蚀对弹丸飞行弹道的影响。谢杨柳等[5]在所建立的六自由度弹丸弹道数学模型基础上，分析各种因素和变量对弹着点位置偏移和概率误差的影响，并重点研究了烧蚀现象对弹道特性的影响。

上述文献均未考虑由于炮口扰动以及弹托分离过程对弹丸初始姿态和飞行稳定性的影响，及其所引起的弹丸飞行弹道的变化。文献[6]分析了电磁发射一体化弹丸的弹托分离过程，并与试验结果进行了对比，但未在此基础上针对其弹道特性进行分析。

1 仿真模型

1.1 刚体六自由度飞行弹道模型

任何自由刚体的运动，都可以看作是刚体的质心运动和围绕质心两种运动的合成，弹体飞行过程中受力示意图如图1所示。其中o-xdydzd，o-x2y2z2，o-ξηζ分别表示平动坐标系、弹道坐标系和第一弹轴坐标系，θ1，δ1，φ2分别表示高低倾角、高低攻角和侧向摆动角[5]。

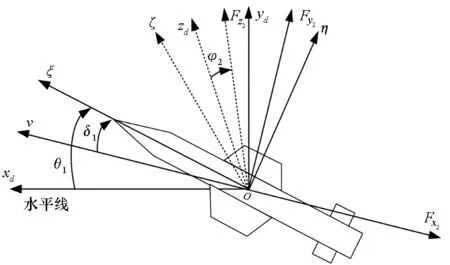
图1 弹体飞行受力示意图Fig.1 Schematic diagram of the force of a projectile

1.1.1 质心动力学和运动学方程

假定弹丸质量均匀分布、弹丸轴对称，由图1可得弹丸的质心动力学方程为：

(1)

其中：Fx2,Fy2,Fz2分别表示外力F(包括重力和气动力)在弹道坐标系三个轴上的分量。

弹丸在地面坐标系下的质点运动学方程为：

(2)

1.1.2 绕质心运动的动力学和运动学方程

弹丸绕质心运动的动力学方程如下：

(3)

其中：A表示赤道转动惯量；C表示极转动惯量，ωξ，ωη，ωζ分别表示弹丸转动角速度在弹轴坐标系下的三个分量；Mξ，Mη，Mζ分别表示弹丸所受外力矩在弹轴坐标系下的三个分量。

弹丸绕质心运动的运动学方程如下：

(4)

其中，φa表示弹轴高低角，γ是弹体自转角(也叫滚转角)。

式(1)～(4)给出了弹丸弹道计算方程组，输入量包括弹丸受到的气动力、重力和气动力矩，且这些输入量与弹丸姿态、速度以及所处的外部环境有关，采用实时反馈计算的方法将耗费大量的计算时间，因此工程上一般基于事先求得的弹丸在各个状态下的气动力、气动力矩数据，采用插值拟合的方法得到弹丸弹道飞行时的各输入量[5]。为便于计算和对比分析，对各气动力和气动力矩采用归一化表示，得到相对应的气动力、力矩系数，如表1所示。

1.2 弹丸出口扰动分析模型

电磁发射一体化弹丸在膛内运动环境复杂，发射过程中弹丸和导轨将发生变形，因此，弹丸以及导轨在发射过程中将产生振动，继而对弹丸出膛时的姿态、速度等产生扰动，从而影响弹丸飞行弹道特性。出膛时，由于炮口初速极高，炮口流场附近会产生强烈的激波与膨胀波结构，这些波系结构不仅影响着弹丸的气动特性，且弹体和弹托头部的激波相互作用，对弹体飞行造成初始扰动。

表1 气动力和气动力矩系数表达式

1.2.1 弹丸炮口扰动分析模型

一体化弹丸在膛内运行时，电枢与导轨之间存在滑动电接触，并带来速度趋肤效应，本文暂不考虑速度趋肤效应对膛内电磁力的影响，因而影响膛内电磁力的因素只有电流频率、电流幅值以及电枢距离炮尾的位置。因此，可通过计算电枢在不同位置处的时谐电磁场得到膛内的磁场分布，并得到在固定电流幅值I0、不同位置l以及不同电流频率ω下的膛内各物体所受电磁力FE。再采用插值拟合的方法得到FE与l和ω的函数关系式。

(5)

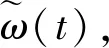
(6)

其中，I(t)表示输入电流。在电磁发射过程中，电枢在膛内受到洛伦兹力，弹丸受到电枢的推力，导轨之间受到相互的排斥力，枢轨接触面还存在电枢电磁力的法向分量。采用式(6)可获得上述力，并将其作为导轨和弹丸线弹性变形动力学控制方程[8]的载荷输入条件，即可求得在电磁力作用下，膛内各物体的运动学和动力学特性，同时考虑到发射过程中电磁力对结构的动力学冲击，在仿真模型中引入Johnson-Cook模型[9]获取材料在高应变率下的动态弹塑性力学响应。

1.2.2 弹托分离仿真模型

一体化弹丸在弹托分离过程中，金属弹托受炮口磁场产生的电磁力以及高马赫来流产生的气动力作用下与弹体分开。因此，一体化弹丸的膛外弹托分离过程涉及磁场与流场的耦合分析。弹丸运动会引起流场的变化，即弹丸运动带动弹丸边界网格的运动，弹丸速度的变化将导致来流边界条件的变化，弹托与弹体位置的变化将引起流场区域网格的变形。而采用动网格技术[10]可有效解决求解域存在运动和变形的问题。

通过建立基于动网格技术并考虑炮口拉弧过程的电磁发射一体化弹丸弹托分离模型，分析弹托分离过程中弹体气动系数的变化情况，图2所示为电磁发射一体化弹丸弹托分离仿真流程图，详见文献[6]。

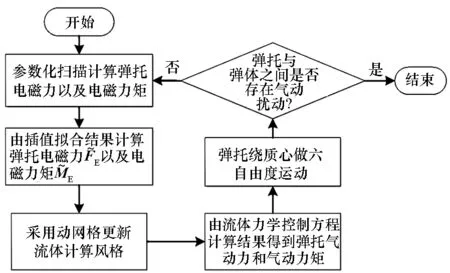
图2 弹托分离仿真流程图Fig.2 Flow chart of simulation of sabot discard process

弹托运动分两个过程[11]：①绕弹托后缘做六自由度运动；②绕弹托质心做六自由度运动。因此，可根据弹托的张开角度θ改变弹托六自由度运动质心，θ的取值根据试验时弹托的张开姿态决定，此处选择θ=π/6。

综上，将炮口扰动引起的弹体速度变化作为式(2)的输入，弹托分离引起的弹体气动系数变化作为式(1)和式(3)的输入，实现弹丸出口扰动模型与弹体六自由度运动方程的耦合，即可建立电磁发射弹丸飞行弹道模型。

2 仿真分析

以IAT设计的电磁发射一体化弹丸[12]为例(如图3所示)，仿真分析考虑弹丸炮口扰动以及弹托分离影响下的弹体飞行弹道特性。

图3(a)中弹托材料选用6061铝，导轨材料选用铜。由于IAT-HVP的电枢和弹托采用一体化设计，因此下文所说的弹托即代表了电枢。

2.1 电磁发射弹丸炮口扰动分析

采用上述电磁力与多体动力学耦合模型分析膛内电磁力的变化特性以及弹丸横法向速度(速度在除轴向方向以外的两个方向的分量)扰动。文献[12]指出，导轨外采用导体封装，但未注明封装尺寸及其固定方式，本文暂不考虑封装的影响，并假定在距离炮尾800 mm和1600 mm上下导轨外表面处设置宽为100 mm的支点约束。

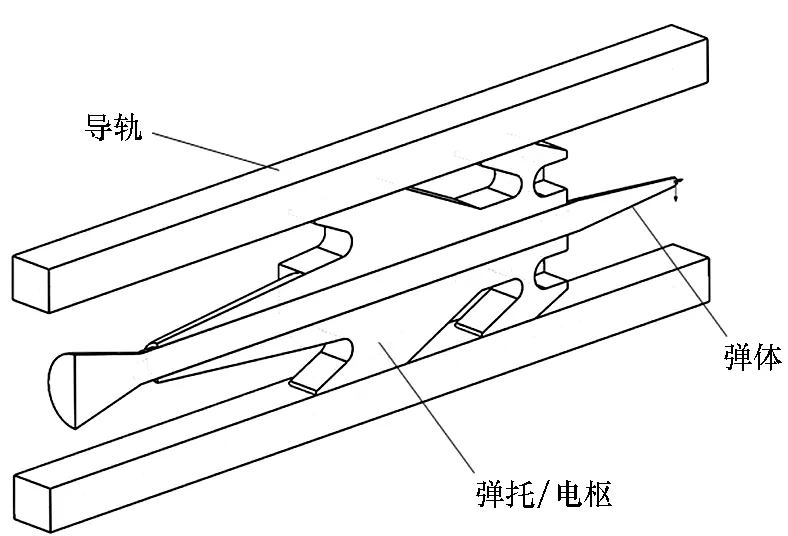
(a) IAT-HVP结构组成(a) Structural components of IAT-HVP

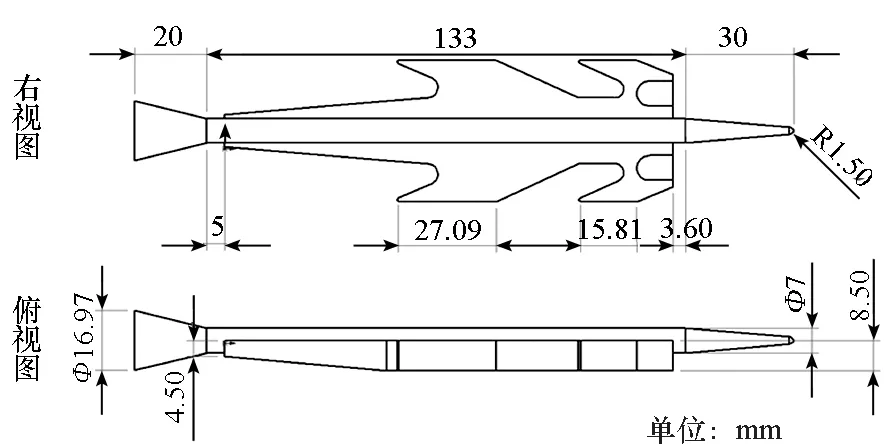
(b) IAT-HVP关键结构尺寸参数(b) Key structure parameters of IAT-HVP图3 电磁发射一体化弹丸IAT-HVP三维模型Fig.3 Three-dimensional model of IAT-HVP

2.1.1 膛内电磁力计算

采用文献[12]中的放电电流数据作为输入激励，对其做时频分析，得到其瞬时频率估计曲线如图4所示。由图可知，在初始段电流频率迅速上升到最大值，峰值为345 Hz，随后电流频率迅速下降，在1.5 ms时电流频率基本为零，这表明此时弹托上的电流分布较为均匀。

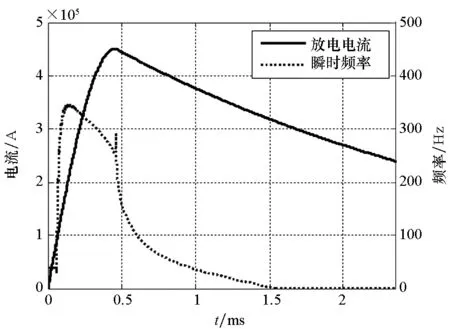
图4 放电电流及电流频率随时间变化曲线Fig.4 Time history of discharge current and current frequency

根据放电电流的瞬时频率估计曲线可知，电流的频率变化范围在0～350 Hz之间，同时由文献[12]可知导轨长度为2.125 m。因此，分析电流幅值为100 kA，电流频率ω∈(0 Hz,350 Hz)，电枢距离炮尾位置l∈(0 m,2.25 m)时弹托和导轨受到的电磁力。

由于电磁力与电流的平方成正比，因此根据图4得到的电流瞬时频率估计曲线，并由弹托位移数据可得弹托在膛内受到的电磁力、导轨单位长度所受排斥力以及弹轨之间的法向电磁力如图5 所示，弹托在膛内的运行曲线如图6所示。

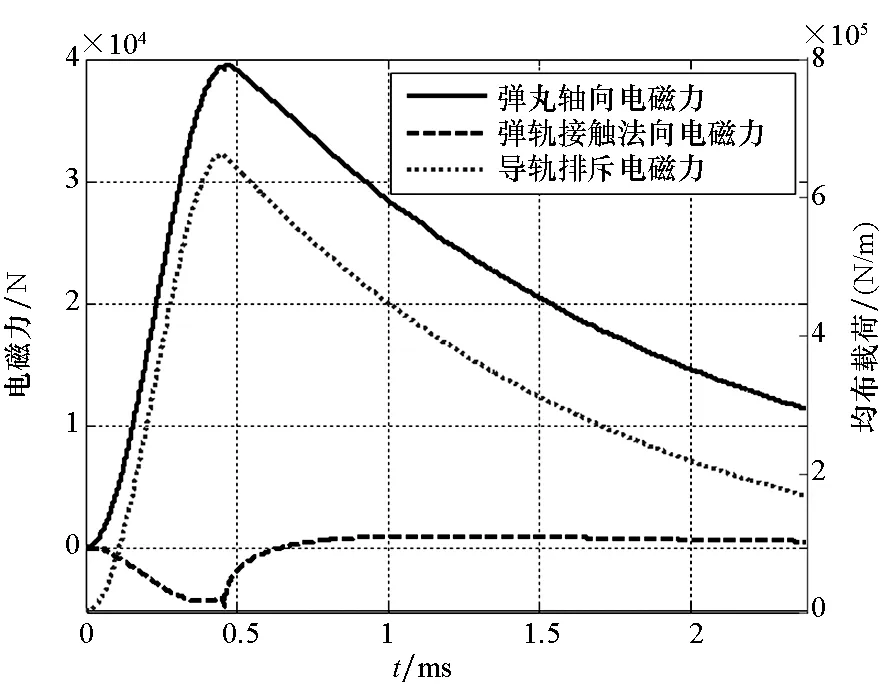
图5 膛内电磁力随弹丸运行时间变化曲线Fig.5 The electromagnetic force varies with the run time of projectile

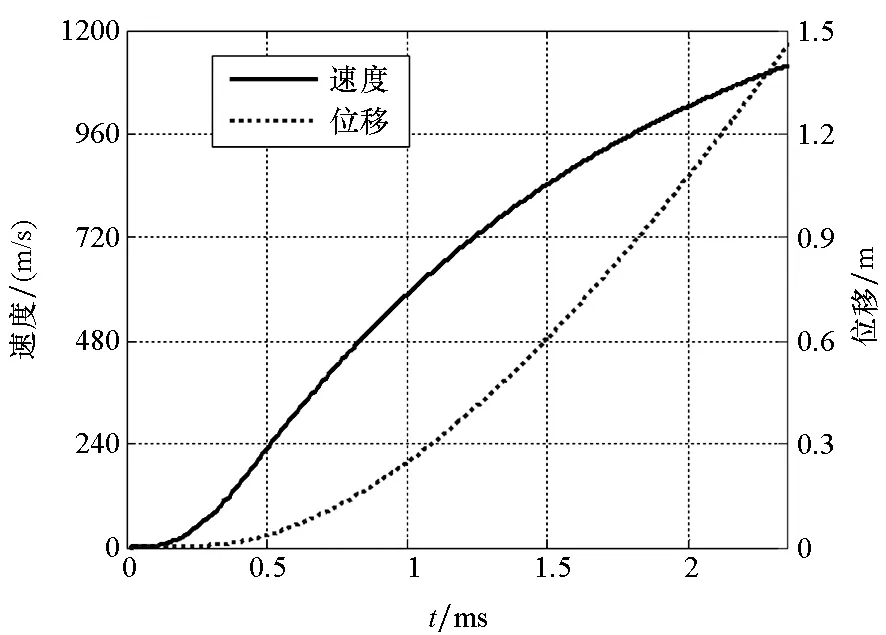
图6 弹丸膛内运动曲线Fig.6 Curves of the projectile travelling in the chamber

图5表明：弹托受到的法向电磁力刚开始为收缩力，随着电流频率的减小逐渐变成扩张力。导轨之间的均布载荷随着电流幅值的增加而加大，电流下降时随之减小。

图6表明：弹托运动位移为1.45 m，出炮口时速度为1117 m/s，与文献[12]中测量得到的炮口初速1117 m/s接近。

2.1.2 弹丸横法向速度扰动分析

弹丸在膛内运动时，受轴向变化电磁力的推动、导轨法向方向的挤压以及由于弹托与弹体的相互作用，导致弹体在膛内出现横法向的扰动，如图7所示。

图7 弹丸横法向速度变化曲线Fig.7 Velocity history of projectile moving in a transverse and normal direction

图7表明：弹丸在膛内运动时上下左右摆动。受导轨固定支点的影响，运动到中间时横法向速度分量较小，弹丸出膛时，横法向速度达到最大(0.25 m/s)，导致弹丸存在0.01°的初始速度倾角。

2.2 电磁发射弹丸出膛气动扰动分析

电磁发射一体化弹丸在弹托分离过程中，会对弹体周围的流场分布造成影响，进而引起弹体气动系数的变化。本节在上述电磁发射一体化弹丸弹托分离模型的基础上，仿真分析IAT-HVP以初速1117 m/s出膛，弹体受到弹托分离扰动后的弹体气动系数变化情况。

上述弹托分离仿真模型的实现，可借助ANSYS仿真平台实现，采用非结构网格划分，并为提高计算精度，对弹托表面设置边界层网格，其中IAT-HVP的表面网格划分如图8所示。经多次试算，取计算域为500 mm×200 mm×400 mm长方体，弹头尖点离长方体顶面的距离为50 mm，弹丸尾端点距离长方体底面167 mm。

图8 IAT-HVP表面网格分布Fig.8 Surface mesh of IAT-HVP

对于边界条件的设定，物面边界采用绝热壁面；计算域外边界为压力远场边界条件，压力为一个标准大气压，来流马赫数由弹丸运动速度确定，温度为300 K。采用用户自定义函数(User Defined Functions, UDF)编写弹托受力及运动方程，实现弹托的六自由度运动。利用弹簧光顺法移动部分网格节点的位置以适应计算域的微小变化，并采用局部网格重划方法对某些网格变形较大区域进行网格重划，以适应计算域的较大变化，仿真结果如图9～11所示。

(a)阻力系数(a) Drag coefficient

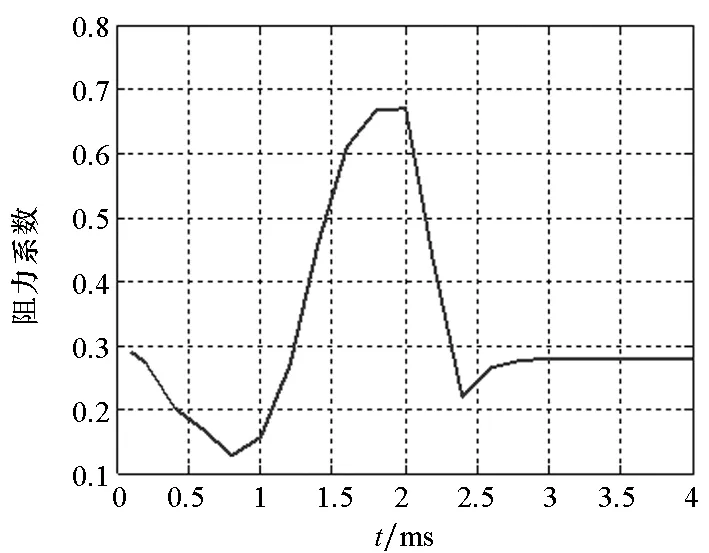
(b)压力分布(b) Pressure distribution图9 弹体阻力系数变化曲线(对称分离)Fig.9 Time history of drag coefficient of projectile (symmetrical separation)

在弹托对称分离情况下，弹体俯仰力矩无变化，但其阻力系数发生变化，如图9所示。在分离起始阶段，由于弹托逐渐远离弹体，弹托前缘激波在弹体表面的激波阻力轴向分量减小，导致弹体阻力系数减小(见0.8 ms时刻弹体和弹托表面的压力分布云图)；随着弹托分开角度的增加，弹托前缘激波打在弹体上的位置后移，并在弹翼附近形成高压，导致弹体阻力系数增加(见2 ms时刻弹体和弹托表面的压力分布云图)；随着弹托分离时间的继续增加，弹托与弹体之间的气动干扰逐渐消失，弹体阻力系数逐渐恢复到正常值(1117 m/s速度下，阻力系数为0.27)。

根据文献[6]的分析结论，弹托分离时间为3～4 ms，在不考虑弹托分离影响的情况下，弹体速度衰减量约3 m/s，因此，分析过程中可不考虑弹体运动速度对弹体气动系数的影响。图10和图11给出了一体化弹丸攻角为2°和4°情况下，弹托分离过程中，弹体阻力系数、升力系数以及压心系数随时间的变化情况。

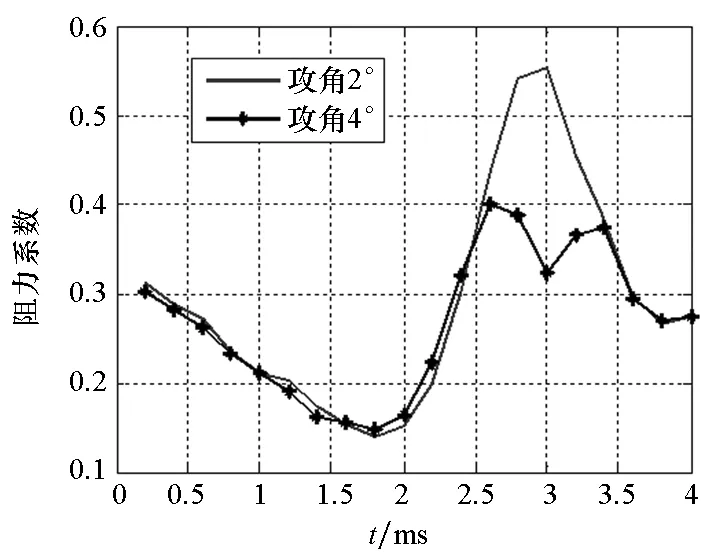
(a) 阻力系数(a) Drag coefficient

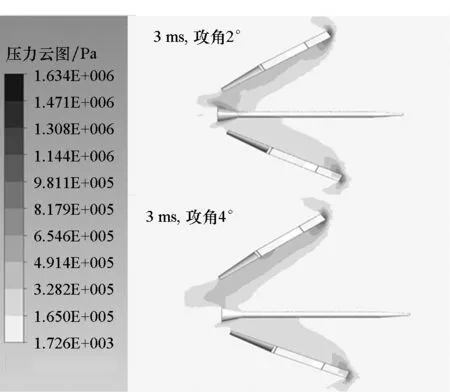
(b) 压心系数 (b) Pressure center coefficient图10 弹体阻力系数变化曲线(非对称分离)Fig.10 Time history of drag coefficient of projectile (asymmetrical separation)

图10和图11表明：非对称分离情况下，弹体阻力系数变化规律与对称情况下一致，但弹体阻力系数波动变小，而波动持续时间变长，即弹托分离带来的气动干扰时间长，且攻角越大，最大波动量反而变小，主要是由于攻角增加，其中一瓣弹托分离加速，导致在弹体尾翼上形成的激波减小(见3 ms时刻攻角为2°和4°时弹体和弹托表面的压力分布云图)。而弹体升力系数和压心系数随着两瓣弹托的张开正负跳动，这表明弹体受弹托分离的影响做上下俯仰运动。

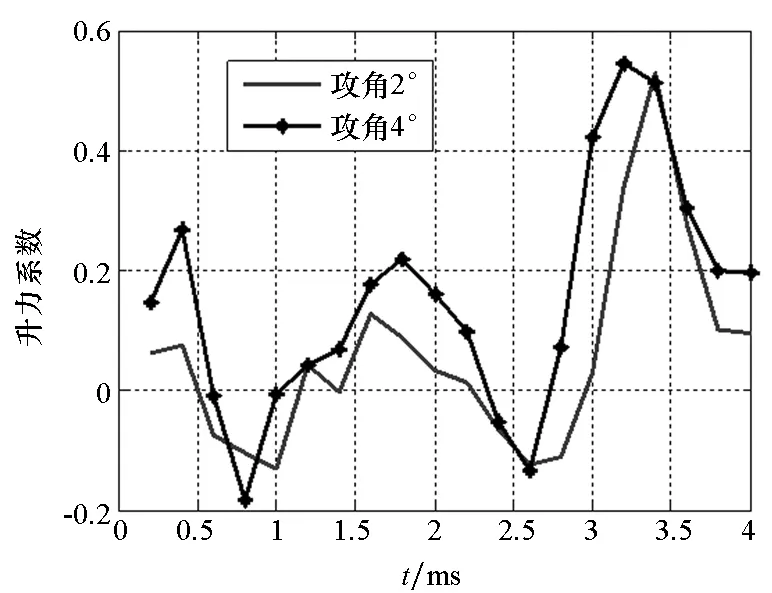
(a) 升力系数(a) Lift coefficient

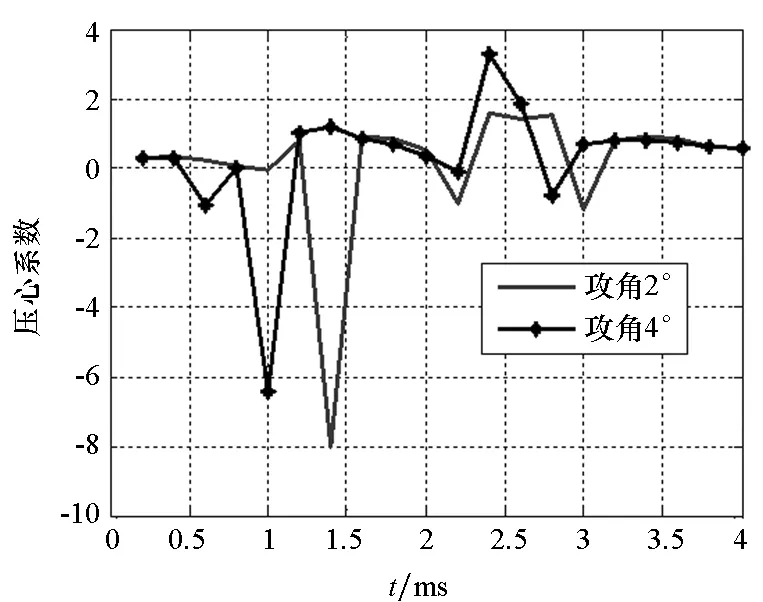
(b) 压心系数 (b) Pressure center coefficient图11 弹体升力系数和压心系数变化曲线(非对称分离)Fig.11 Time history of lift coefficient and pressure center coefficient of projectile (asymmetrical separation)

根据0°、2°和4°攻角情况下弹托分离对弹体阻力系数的影响结果，通过插值拟合，可得到弹体阻力系数随攻角和时间的变化关系式如下：

(7)

2.3 弹道仿真与分析

2.3.1 气动系数仿真

对IAT-HVP弹体进行气动特性分析，建立300 mm×200 mm×350 mm的空气域，网格划分如图12(a)所示，网格节点数量为825 762，仿真计算其在不同攻角、马赫数下的气动系数，如图12(b)～(e)所示。

图12表明：随着攻角的增加，弹体阻力系数、升力系数和升阻比逐渐增加，压心系数逐渐减小，弹体气动稳定性变差；随着马赫数的增加，弹体阻力系数减小，而升力系数增加，这是由于弹体尾部采用“尾裙”结构，且弹体长细比较大，导致升力系数随马赫数的增加而减小[13]，与文献[14]中的计算结果规律一致；升阻比随着马赫数的增加逐渐变大，这表明弹体机动性能增加。

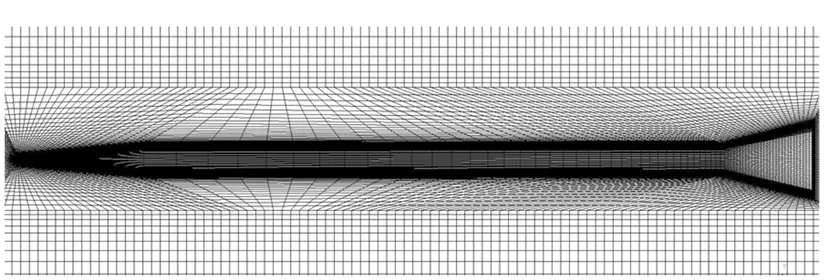
(a) 弹体网格划分(a) Mesh generation of projectile

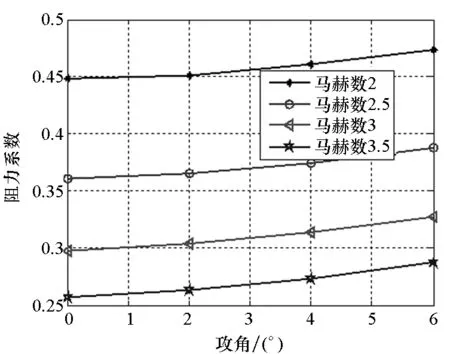
(b) 阻力系数变化情况(b) Variation of drag coefficient

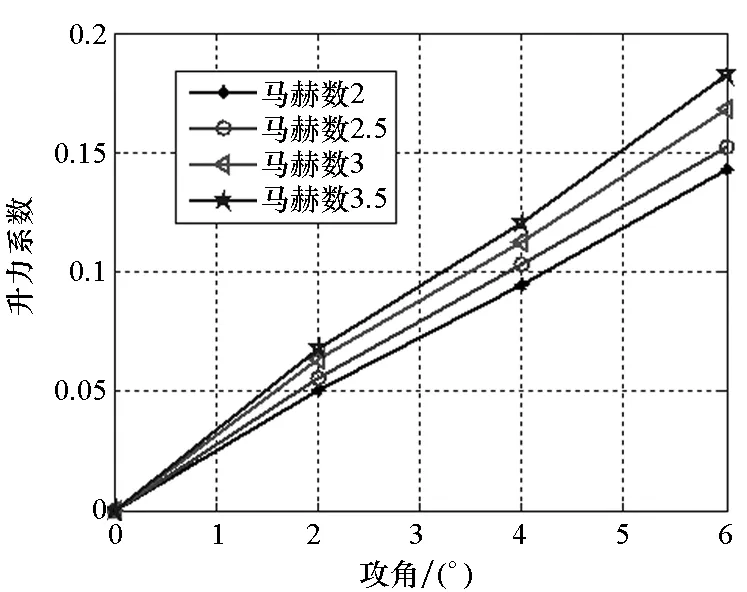
(c) 升力系数变化情况(c) Variation of lift coefficient

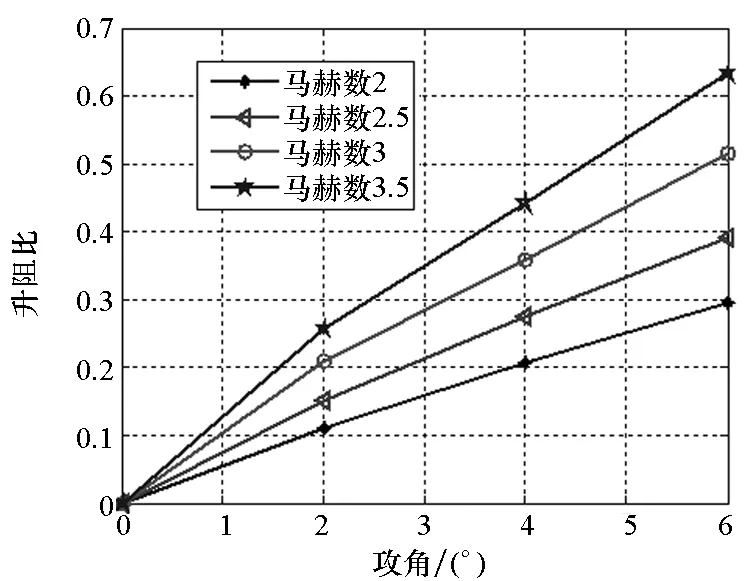
(d) 升阻比变化情况(d) Variation of lift-drag ratio

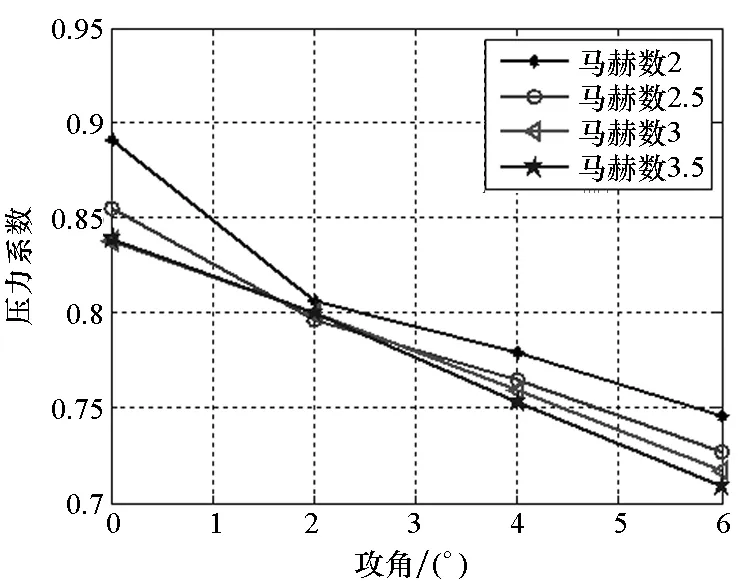
(e) 压心系数变化情况(e) Variation of pressure center coefficient图12 弹体气动系数仿真Fig.12 Simulation of AD coefficient of projectile

2.3.2 弹道仿真

基于上述分析，采用仿真得到的IAT-HVP出膛速度作为弹道仿真速度输入，仿真IAT-HVP以炮口初速1117 m/s，射角0°，射程200 m时的弹道。分别得到理想情况以及考虑弹丸出口扰动情况下的弹道曲线，如图13所示。

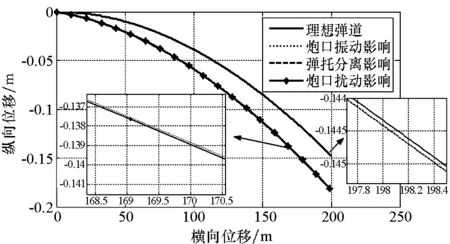
图13 弹丸运动轨迹Fig.13 Motion trajectory of projectile

图13表明：正常情况下弹体往下偏移147.2 mm，考虑弹丸出口扰动时弹体往下偏移182.7 mm，相比理想弹道产生了24%的偏差。单独考虑炮口扰动以及弹托分离情况下的弹体落靶偏移量为182.6 mm和147.3 mm。上述结果表明：影响电磁发射弹丸落点偏差最主要的因素是炮口扰动引起的弹丸速度偏差，其次是弹托分离的影响。

3 结论

电磁发射一体化弹丸的发射原理与常规炮弹存在本质的差异，导致其初始弹道特性和分析方法均不同于常规弹药。本文针对电磁发射弹丸的发射特点，建立了考虑弹丸炮口扰动以及弹托分离过程影响下的电磁发射弹丸刚体六自由度运动方程，仿真分析了IAT-HVP弹丸炮口扰动对弹体速度和气动特性的影响，并得到其飞行弹道曲线。仿真结果表明：炮口扰动引起了0.01°的速度倾角，而弹托分离过程将引起弹体气动系数的改变，进而引起落点的偏差，其中炮口扰动引起的偏差远大于弹托分离引起的落点偏差。本文的分析方法和结论可为一体化弹丸的作战使命任务分析提供依据。