计及摩擦的摆线轮齿与针齿的分形接触模型
2019-07-29韩炬李威董威
韩 炬 李 威 董 威
1.北京科技大学机械工程学院,北京,1000832.华北理工大学机械工程学院,唐山,063210
0 引言
摆线针轮传动机构是工业机器人关节减速器的关键部件,目前关于摆线针轮传动啮合接触特性的研究主要采用基于赫兹理论的方法[1-4]和有限元方法[5-8],这两类方法均未考虑接触表面微观形貌对接触特性的影响。此外,文献[9-10]提出了一种精确预估摆线针轮接触时的啮合齿数并确定接触点的实际位置,进而获取接触载荷的动力学分析方法,并考虑轴承的影响,对摆线针轮接触非线性力学系统进行建模与分析;文献[11]应用影响系数法,对二齿差摆线针轮的接触特性进行了分析。以上分析均是针对摆线针轮的宏观接触面进行的数值分析。文献[12]综合考虑了摆线针轮的宏观轮廓、接触应力以及齿面的粗糙度、传递效率等参数,建立了摆线针轮综合润滑性能分析模型,但在接触应力的分析中并未考虑接触面微观形貌的影响。
自文献[13]提出分形理论以来,其应用非常广泛。文献[14]指出机械加工面具备明显的分形特征。文献[15-16]提出的MB分形接触模型是近年来众多相关研究的基础模型,MB模型采用Weierstrass-Mandelbrot函数(简称“W-M函数”)模拟粗糙平面的表面形貌,但由其推论出的“接触面积小时发生塑性变形而接触面积大时发生弹性变形”的结论,与经典接触理论相左。MB模型以及针对MB模型的缺陷提出的ME模型[17-18]是现有分形接触模型的典型代表,两种模型的对象是两粗糙平面之间的接触,但实际的机械零件之间的接触多是粗糙曲面之间的接触。文献[19-21]提出的HC模型对两粗糙圆柱面之间的接触特性进行了分析,该模型中引入了接触系数,但该系数的构建只考虑了宏观特征,且该接触系数不能准确反映两接触曲面接触面积的大小。
机械结合面的微观形貌及表面接触特性对零部件的表面摩擦磨损性能有显著的影响。综合宏观和微观因素,对机器人关节减速器中静态及动态结合面的接触机理进行深入研究,对提升我国工业机器人关节减速器的研发水平意义重大。本文以单对摆线轮齿与针齿接触为研究对象,综合考虑接触曲面的宏观和微观特征,计及摩擦因素的影响,建立了其分形接触模型,为进一步确定多齿啮合的摆线针轮传动机构的时变接触特性提供了理论参考。
1 摆线轮齿与针齿的形貌模型
1.1 基于W-M函数与矢量函数的表面形貌模型
要准确分析摆线轮齿与针齿的接触特性,需要构建合理的表面形貌模型。粗糙曲面可以看作是在光滑曲面上随机分布高度、大小不等的微凸体,综合应用W-M函数和矢量函数表征粗糙曲面的表面形貌。粗糙曲面的表面形貌见图1,由图1可知:
r*=r±z(s)m
(1)
式中,z(s)为向量r的方向上对应的微凸体的高度[22];s为曲面截面曲线的弧长;m为曲线上K点的单位法向量;G为特征尺度[23];Ra为接触表面粗糙度,μm;D为分形维数,D=1.528Ra-0.042[24];γn为粗糙曲面的空间频率,γ>1,一般取γ=1.5;n为频率指数;nmin为最低频率指数;rθ、rθθ分别为r对θ的一阶导数与二阶导数;“±”与曲线的凹凸有关,当曲线内凹时取“+”,当曲线外凸时取“-”。

图1 粗糙曲面表面形貌图Fig.1 Plot of rough surface
由式(1)可知,针齿的表面形貌模型为
(2)
G=105.26Ra-0.042
式中,rp为针齿半径。
图2为在MATLAB中绘制的针齿表面形貌图,其中,D=1.542 4,G=4.903 1 nm,nmin=1。

(a)原始比例

(b)100倍显示

(c)1 000倍显示图2 针齿分形形貌图Fig.2 Fractal topography of pin tooth
经过等距修形与移距修形的摆线轮齿的表面形貌模型为
(3)
rc(θ)=(x(θ),y(θ))
式中,rc(θ)为光滑摆线轮齿上一点的矢径;Rb为基圆半径;Rg为滚圆半径;ΔRb为移距修形量;ΔRp为等距修形量;e为针齿中心与滚圆圆心的中心距;i0为摆线轮与针轮的相对传动比;K1为摆线轮短幅系数,K1=eZp/Rg;Zp为针轮齿数;mc为光滑摆线轮齿上一点的单位法向量;s*为起点到啮合点的弧长。
图3为在MATLAB中绘制的单个摆线轮齿的表面形貌图。
(a)原始比例 (b)100倍显示

(c)1 000倍显示图3 摆线轮齿分形形貌图Fig.3 Fractal topography of cycloid tooth
应用FEI QUANTA 650扫描电子显微镜,对摆线轮齿齿廓进行测试。图4为线切割得到的单个完整摆线轮齿的电镜测试图,对比图4与图3,可以看出,式(3)对摆线齿轮轮齿表面形貌的模拟具有高度合理性。

(a)线切割摆线齿轮轮齿测试样品

(b)电镜测试放大100倍图

(c)电镜测试放大1 000倍图图4 摆线轮齿电镜测试图Fig.4 Electron microscope test images of cycloid tooth
1.2 摆线轮齿与针齿的接触比例系数
现有基于分形理论的粗糙面接触模型的研究对象大多为粗糙平面,但摆线轮齿与针齿均为粗糙曲面,其接触面积远小于平面之间的接触面积,文献[19-21,25]均提出了粗糙曲面接触时的接触系数概念,但已有文献中对构建的曲面接触系数只具备初步的合理性,且接触系数体现了宏观特征的影响。现有研究结论包括:接触系数不大于1;内接触时接触系数大于外接触时的接触系数;当两圆柱面半径一致时,内接触时接触比例系数等于1。由文献[19-21,25]的数据及曲线可知,当两等半径的圆柱面外接触时,接触比例系数的值接近0.85,该值显然不合理。
结合曲面表面形貌模型,综合考虑曲面的宏观特征和微观特征,采用笔者前期研究过程中构建的接触比例系数λcp[26]:
(4)

式中,n*为微凸体等级;lt为微凸体的截断长度;l为微凸体基底长度;ρp为针齿上接触点的曲率半径,此处为针齿半径;ρci为摆线轮齿上第i个接触点的曲率半径;ρi为第i个接触点的综合曲率半径[3];φi为啮合相位角,φi∈[0,2π];Rz为针轮中心圆半径;θp为针齿曲面与光滑平面的临界接触角度;θcp为摆线轮齿曲面与光滑平面的临界接触角度。
图5所示为各参数对摆线轮齿与针齿的接触比例系数的影响。从图5中可知,摆线轮齿与针齿的接触比例系数始终小于1,且针齿与摆线轮齿的内凹部分接触时的接触比例系数远大于与摆线轮齿的外凸部分接触时的接触比例系数;接触比例系数随分形维数的增大而减小;随特征尺度的增大而增大;随摆线轮与针轮中心距的增大先增大后减小;随针齿半径的增大而增大;随针轮齿数的增加而增大。由以上分析可知,本文构建的接触比例系数很好地体现了针齿与摆线轮齿接触过程中的时变特性。

(a)分形维数(e=0.9 mm,rp=2 mm,Zp=40,G=4.903 1 nm) (b)特征尺度(e=0.9 mm,rp=2 mm,Zp=40,D=1.542 4) (c)中心距(rp=2 mm,Zp=40,D=1.542 4,G=4.903 1 nm)

(d)针齿半径(e=0.9 mm,Zp=40,D=1.542 4,G=4.903 1 nm) (e)针轮齿数(e=0.9 mm,rp=2 mm,D=1.542 4,G=4.903 1 nm)图5 各参数对接触比例系数的影响Fig.5 Influence of parameters to contact coefficient
2 考虑摩擦因素的分形接触模型
在分析中引入摩擦因素是近年来分形接触模型的重点研究方向[20,27-29],本文构建的摆线轮齿与针齿的分形接触模型中也体现了摩擦因素的影响。
2.1 摆线轮齿与针齿接触面积分布
摆线轮齿与针齿的啮合接触属于典型的高副接触,且接触过程中,摆线轮齿的曲面曲率是时变量,结合所提出的接触比例系数与文献[15]中对分形接触面积分布的推导可知,摆线轮齿与针齿啮合时的接触面积分布为
(5)
式中,A为粗糙表面微凸体的接触面积;Amax为微凸体的最大接触面积。
2.2 摩擦影响下的摆线轮齿与针齿接触模型
2.2.1微凸体接触变形模型
李小彭等[27]以MB模型为基础,进行了考虑摩擦的结合面分形模型分析,得出了微凸体弹塑性变形的临界面积,然而MB模型假设微凸体变形量为微凸体的整个高度,该假设并不合理。从图6所示的微凸体接触变形简图中可知,微凸体的变形量ω与微凸体的高度δ不一致,且0≤ω≤δ,ω的表达式为
(6)
δ=GD-1l2-D

图6 微凸体与刚性平面接触变形简图[11]Fig.6 Schematic of deformation of an asperity with a rigid flat plan in contacting[11]
由赫兹接触理论可知,微凸体的临界弹性变形阶段的接触面积
(7)
式中,R为微凸体顶端曲率半径。
发生塑性变形的临界变形量
(8)
式中,H为材料的硬度;K′为硬度系数,一般取K′=0.454+0.41ν;E为弹性模量;ν为泊松比。
此时的接触载荷[17]
(9)
综合式(7)、式(9)可得
(10)
当接触曲面之间存在滑动摩擦时,接触压力P[24]满足:
P=1.1kμσy
(11)
式中,σy为材料的屈服强度;kμ为摩擦因子μ的分段函数,当0≤μ≤0.3时,kμ=1-0.228μ,当0.3<μ≤0.9时,kμ=0.932e-1.58(μ-0.3)。
将式(11)代入式(10)可知,计及摩擦影响时,弹性变形面积
(12)
从式(12)可知,弹性变形面积为尺度相关量。
微凸体发生弹塑性变形的临界变形面积[27]
(13)
2.2.2摆线轮齿与针齿的接触面积及接触载荷
粗糙曲面接触时,参与接触的微凸体可能存在3种变形状态,依次为完全弹性变形、弹塑性变形和完全塑性变形,弹塑性变形阶段又可以分为第一塑性变形区域与第二塑性变形区域。KOGUT等[30]对微凸体的3种变形状态进行了细致的研究,成雨等[31]根据KOGUT等的研究对粗糙面的接触面积与接触载荷进行了推导。
摆线轮齿与针齿的真实接触面积
Ar=Are+Arep1+Arep2+Arp
(14)
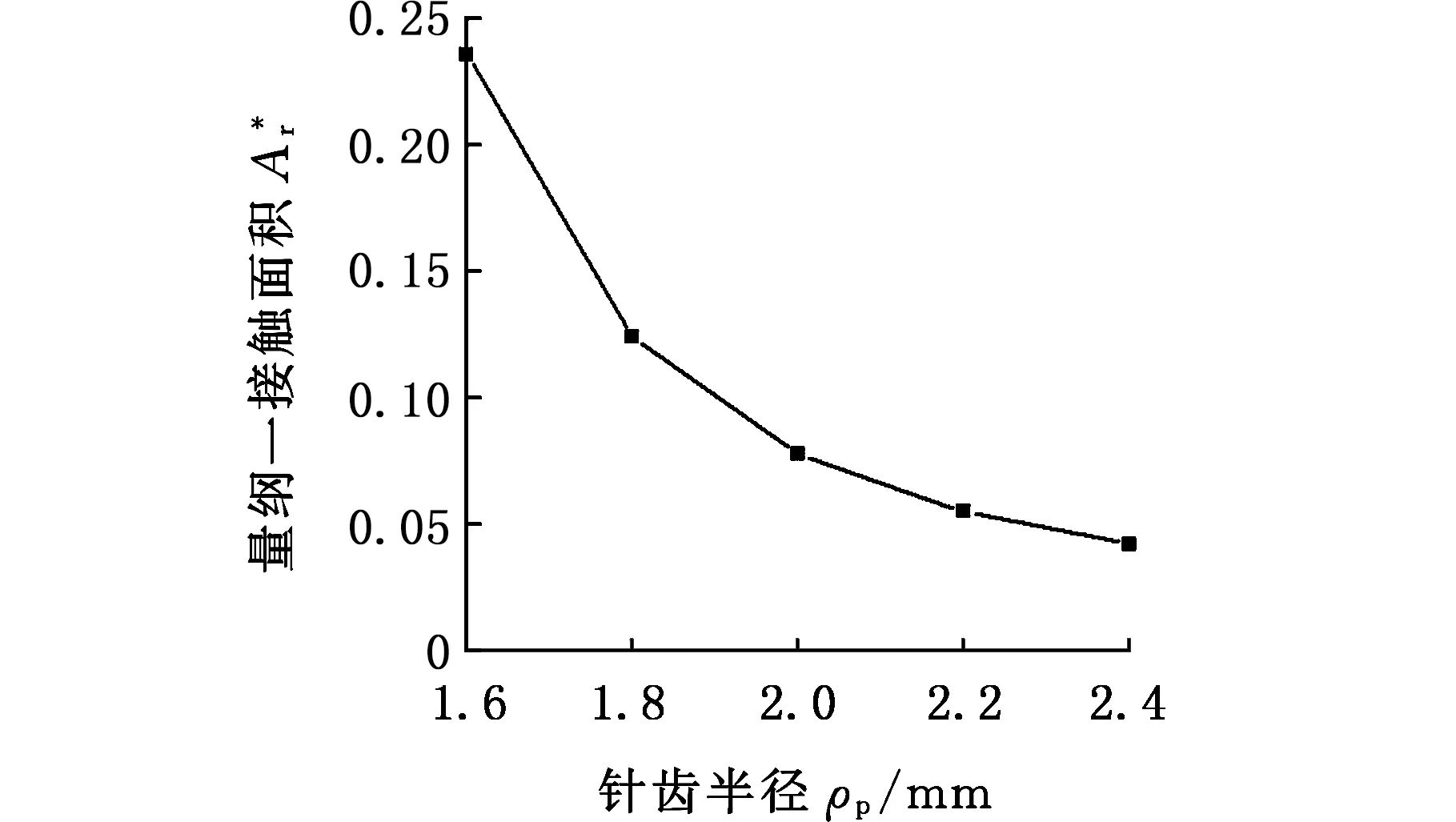
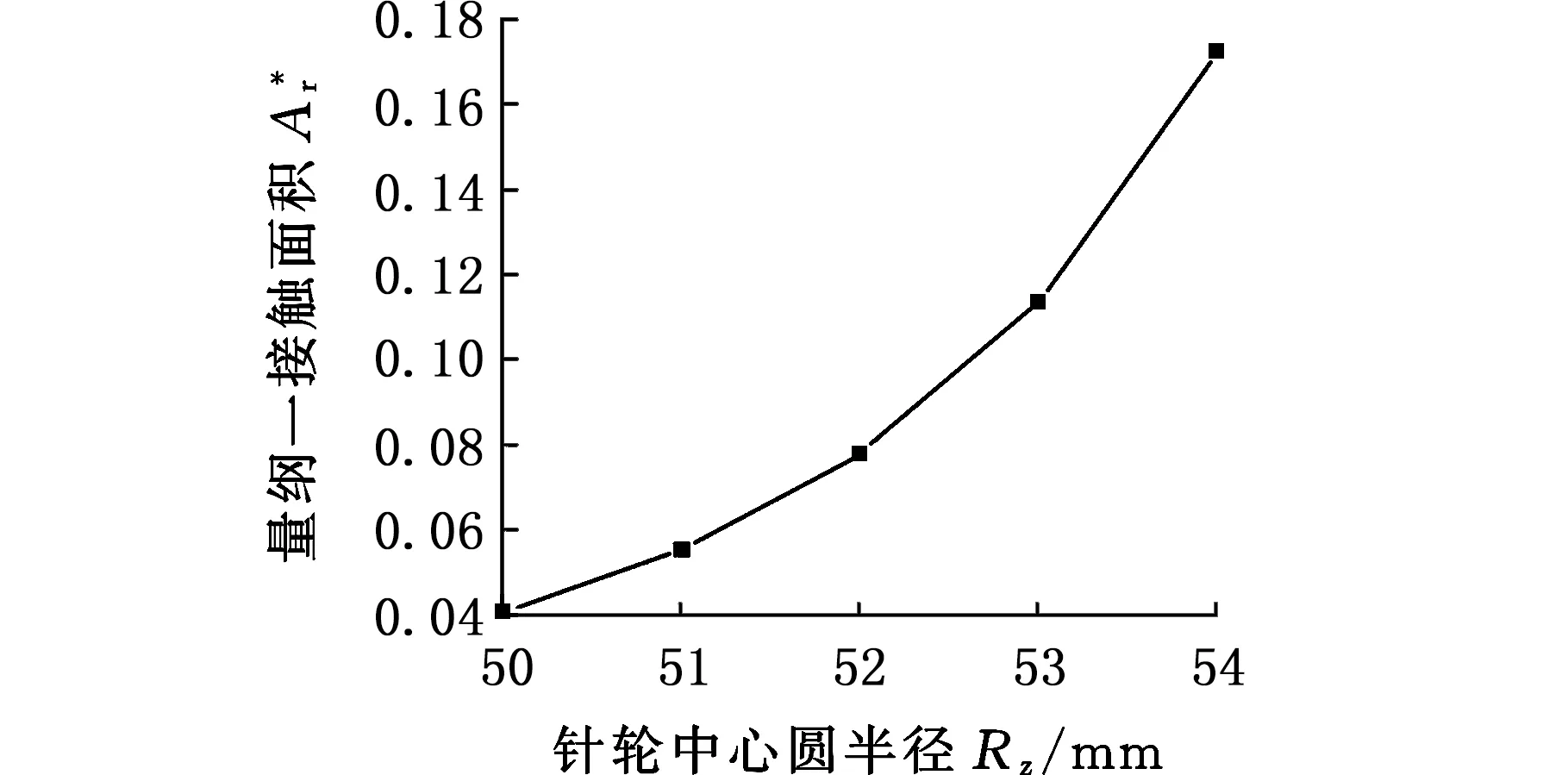
ψ=5.453e-D/0.628+1.499 1 式中,Are为发生弹性变形的微凸体的总接触面积;ψ为分形区域扩展系数[32];Arep1为发生第一塑性变形的微凸体的总体接触面积;Arep2为发生第二塑性变形的所有微凸体的接触面积;Arp为发生完全塑性变形的微凸体的接触面积;Aepc为微凸体第一塑性变形的临界面积;Aμpc为微凸体完全塑性变形的临界面积。 摆线轮齿与针齿的接触载荷 Fr=Fre+Frep1+Frep2+Frp (15) [(205.382 7Aμec)1.102 1-0.5D- 式中,Fre为弹性变形部分的接触载荷;Frep1为第一弹塑性变形部分的接触载荷;Frep2为第二弹塑性变形部分的接触载荷;Frp为完全塑性变形部分的接触载荷。 摆线轮齿与针齿的接触载荷与真实接触面积之间的量纲一关系为 (16) 2.2.3微凸体的等级 微凸体等级系数n*(n*≤nec)直接决定了微凸体所处的状态,根据成雨等[31]的研究,可知微凸体弹性临界等级: (17) 第一弹塑性临界等级 (18) 第二弹塑性临界等级 (19) 当n*≤nec时,微凸体处于完全弹性变形状态;当nec 以RV-20E型减速器为例,其基本参数如表1所示。 取G=4.903 1 nm,D=1.542 4,l=0.01 mm,可知本例中微凸体的等级n*=12,而nec=10,nepc=14,即nec 表1 RV-20E型减速器摆线轮基本参数Tab.1 Parameters of cycloid in RV-20E reducer 根据式(16)的分形接触模型,不同摩擦条件下摆线轮齿与针齿接触时,量纲一接触载荷与接触面积之间的关系见图7,图7中的数据为最大的接触面积与相应的接触载荷,由于摆线轮齿与针齿接触时其接触载荷和接触面积为时变量,通过对其他接触点的相应接触载荷和接触面积的分析,发现该变化规律与图7相同,因此图7具备代表性。 图7 摩擦因素对接触特性的影响Fig.7 Influence of friction factor to contact characteristic 从图7可看出相同载荷下,接触面积随摩擦因素增大而增大,当μ≤0.3时,相同载荷下,真实接触面积的增幅很小,μ>0.3时,真实接触面积的增幅较大。本文的结论与文献[33]所得结论相反,文献[33]的接触模型是基于MB模型的,其结论是当接触面积较大时发生弹性变形,接触面积较小时发生塑性变形,该结论有悖于常识及经典接触理论。 相同载荷条件下,结合面越粗糙,其接触面积越大是显而易见的,本文的结论与文献[32,34]的结论一致。 分形维数D与特征尺度G两个微观特征均与表面粗糙度Ra有关,图8所示为固定量纲一接触载荷下,结合面粗糙度对接触面积的影响。 图8 结合面微观特征对接触面积的影响Fig.8 Influence of contact area by microscopic feature 当粗糙度为0.4 μm时,微凸体处于完全弹性变形状态;当粗糙度为0.8 μm时,微凸体处于弹性变形与第一弹塑性变形状态;当粗糙度为1.6 μm、3.2 μm、6.3 μm时,微凸体处于弹性变形、第一弹塑性变形与第二弹塑性变形状态。 从图8可知,量纲一接触面积随结合面粗糙度先增大后减小。当粗糙度为1.6 μm时,量纲一接触面积最大;当粗糙度为0.4 μm时,由于结合面较光滑,微凸体的高度差相对较小,微凸体均处于弹性变形;当粗糙度增大到1.6 μm时,接触面粗糙程度加大,发生塑性变形的微凸体增多,使得量纲一接触面积增大;当粗糙度继续增大时,微凸体起伏加剧,虽然部分微凸体已经处于第二弹塑性变形状态,但由于接触面粗糙程度进一步增大,微凸体高度增加,实际发生接触的微凸体反而减少,致使量纲一接触面积减小。由此也可推知摆线轮与针轮的粗糙度并不是越大越好。 摆线轮的齿廓相对比较复杂,图9所示为结合面在相同量纲一接触载荷下,各宏观特征对量纲一接触面积的影响。从图9中可看出,量纲一接触面积随针齿半径的增大而减小,随中心距的增大而减小,随针轮中心圆半径的增大而增大,随针轮齿数的增加而减小。 (1)构建的摆线轮齿与针齿的接触比例系数与摆线轮齿的轮廓曲率相对应,具有时变性。结合面的宏观特征与微观特征对接触比例系数均有影响,当摆线轮齿的外凸部分与针齿接触时,接触比例系数远小于摆线轮齿的内凹部分与针齿接触时的接触比例系数,接触比例系数的值始终小于1。 (a)针齿半径对量纲一接触面积的影响 (b)中心距对量纲一接触面积的影响 (c)针轮中心圆半径对量纲一接触面积的影响 (d)针轮齿数对量纲一接触面积的影响图9 结合面宏观特征对接触面积的影响Fig.9 Influence of contact area by gross feature (2)考虑摩擦因素,构建的摆线轮齿与针齿的分形接触模型中,结合面的接触载荷与接触面积不仅与摩擦因素有关,还与结合面微观特征以及宏观特征有关,相同载荷下,接触面积随摩擦因素的增大而增大,当μ≤0.3时,真实接触面积的增幅较小,μ>0.3时,真实接触面积的增幅较大。 (3)结合面粗糙度变化时,由于表面形貌的变化,微凸体的变形状态也存在动态变化,相同载荷下,接触面积随结合面粗糙度的增大先增大后减小,因此摆线轮齿与针齿的粗糙度并不是越大越好。 (4)相同载荷下,接触面积随针齿半径、中心距、针轮齿数的增大而减小,随针轮中心圆半径的增大而增大。 (5)本文构建的分形接触模型重点研究了单对摆线轮齿与针齿的接触特性,关注了微观形貌与宏观特征对接触特性的影响。摆线针轮传动机构属于多齿啮合机构,后续将考虑润滑介质的影响,并结合本文构建的模型,通过针对性试验对摆线针轮机构的总体接触特性及热特性进行深入分析。
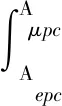


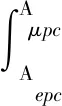


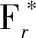
3 摆线轮齿与针齿分形接触模型特性分析

3.1 摩擦因素对接触特性的影响

3.2 微观特征对接触特性的影响

3.3 宏观特征对接触特性的影响
4 结论