基于MIV-BP模型和AIC准则的盾构掘进参数优化研究
2019-07-27张社荣和孙文
张社荣,方 鑫,和孙文
(1.天津大学水利工程仿真与安全国家重点实验室,天津 300072;2.天津大学建筑工程学院,天津 300072;3.中国水利水电第十四工程局有限公司,昆明 650051)
引言
近年来,轨道交通事业的发展和盾构施工技术的进步为水下隧道和隧洞建设提供了基础,越来越多的过海穿江隧道和隧洞项目,诸如武汉长江隧道、南京长江隧道、温州市域铁路S2线、大连地铁5号线跨海盾构工程等,已采用盾构法在我国的内陆及沿海地区建设完成或正在施工[1,2]。然而由于水下隧道和隧洞工程所处的特殊的施工环境,依然存在一些亟待解决的关键技术问题:因地层条件复杂多变,多种地层复合交互,且软弱地层均存在,导致盾构施工过程中掘进参数差异性很大[3],复合地层条件下掘进参数的选择与控制一直是难点问题[4]。
目前,对于复合地层下掘进参数的选择与控制的研究工作主要集中在经验公式推算、数理统计、模拟仿真和智能反演计算方面,取得了有效的成果。在不同的复合地层盾构施工过程中,依托实际工程现场采集的变形监测数据,结合经典理论公式推算,是获得掘进参数取值范围的重要手段[5-8]。另外,大多数学者针对典型区间地段不同的复合地层,利用数理统计方法对施工过程中关键掘进参数与主要地层的相关性进行详尽的分析,并近似将关键掘进参数视为服从正态分布[3,9-11]。数值模拟方面,徐新等[12]采用ABAQUS模拟盾构施工过程,进而分析优化掘进参数;陈秋鑫等[13]采用数值模拟方法分析盾构穿越复合地层时产生的地表沉降,并结合实际监测数据,引入施工风险思想提出更安全的掘进参数。智能反演计算方面,李超、朱北斗、孙谋等[14-16]采用BP人工神经网络方法建立复合地层条件下关键掘进参数预测模型,对关键掘进参数的取值进行分析、预测、验证;而邵成猛[17]则是通过对关键掘进参数在不同地层条件下变化规律的分析,总结出依托于关键掘进参数的学习向量量化LVQ神经网络的地层识别方法。
上述4种方法推动了复合地层下掘进参数的选择与控制的研究工作,但仍存在部分缺陷。
(1)采用盾构法进行水下隧道和隧洞施工中,由于地质条件复杂,存在的复合地层造成掘进参数存在非线性、时变性等不确定因素,现阶段总结的公式往往存在较大的误差,如何将掘进参数与相应的复合地层关系采用准确的显示函数加以表示,还有大量的工作要做。
(2)采用模拟仿真研究掘进参数与复合地层关系的方法,建模时无法考虑到施工中新揭露的地质及开挖、支护等时变的因素,且计算需花费大量的时间,无法及时对掘进参数进行预测和控制,进而无法实时有效的指导现场施工。
(3)对于关键掘进参数的选取,常凭经验,具有很强的不确定性和动态性,导致基于智能反演方法建立的关键掘进参数预测模型常不准确;同时,将关键掘进参数近似视为服从正态分布,也是造成无法获得与复合地层相适应、准确的掘进参数值的因素之一。
以陆丰核电站1、2号机组海底排水隧洞工程为依托,采用BP(Back Propagation)人工神经网络方法建立掘进参数预测模型,在此基础上,引入MIV方法筛选出对盾构施工效果影响显著的关键掘进参数,并根据AIC准则,确定对应复合地层条件下掘进参数服从的最优分布,提出以50%和90%置信水平下的置信区间,分别作为掘进参数的控制区间和预警区间的掘进参数优化设计方案,以指导后续施工。最后,为简化掘进参数的分析过程,提高分析效率,基于Python开发了掘进参数优化分析程序。
1 研究方法
1.1 基于MIV-BP模型的关键掘进参数选择
BP神经网络是一种信号前向传递,误差反向传播的多层前馈神经网络,网络结构是由输入层、一层或多层隐层和输出层组成,它的相邻两个层之间的各个神经元相互全连接,同层内的神经元间无连接。理论已证明,三层BP网络可以在保证精度的情况下实现对任何复杂的非线性函数的逼近[18]。因此,为简化分析过程,保证预测精度,本文选择单隐层的三层BP神经网络结构建立掘进参数的预测模型。平均影响值(MIV, Mean Impact Value)是由Dombi[19]等人提出的用来反映神经网络中权重矩阵的变化情况,可以用来测定出神经网络的输入参数对于输出参数的影响权重,其符号代表相关方向,绝对值大小反映影响的相对重要性。
本文提出的基于MIV-BP模型的关键掘进参数选择,其具体的实现过程如图1所示:(1)在BP神经网络训练终止后,每次把训练样本P里的某一个输入参数(掘进参数)在其原来值的基础上分别加、减一定的比例(如10%),构成两个新的训练样本P1、P2;(2)将P1、P2分别作为仿真样本利用已建成的BP神经网络模型进行仿真,得到两个仿真结果(隧洞拱顶沉降量)A1、A2;(3)计算A1、A2的差值即为变动该输入参数对输出参数产生的影响变化值(IV,Impact Value);(4)根据观察次数对影响变化值求平均,可获得对应输入参数的MIV值。重复上述过程,可以计算出每个输入参数的MIV值,根据MIV绝对值的大小,可以判断出每个输入参数对神经网络输出结果的影响权重,即每个掘进参数对拱顶沉降量影响的相对重要性。
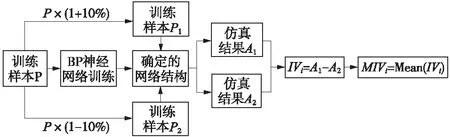
图1 基于MIV-BP模型的关键掘进参数选择流程
1.2 基于AIC准则的关键掘进参数最优分布的确定
赤池信息准则(Akaike information criterion,AIC)是用来权衡统计模型拟合优劣的标准,能够衡量所估计模型的复杂程度和模型拟合数据的能力。AIC准则是识别最优的概率分布函数的重要方法,且AIC值最小的概率分布函数,拟合原始观测数据的效果最好。通常情况下,AIC定义为
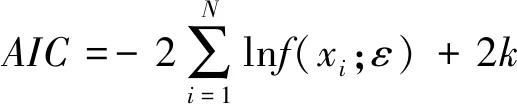
(1)
式中,f(·)为拟合原始观测数据的概率分布密度函数;{xi,i=1,2,3,…,N}为原始观测数据,其中N为样本个数;k为概率分布函数中分布参数的个数。根据上式,即可由盾构施工过程中采集到的掘进参数实测值计算出多种概率分布函数的AIC值,通过对比AIC值的大小,即可找出拟合关键掘进参数概率分布特性最优的概率分布函数。
本文提出的基于AIC准则的关键掘进参数最优分布的确定方法,主要通过所开发程序引入的开源的SciPy模块库实现。程序共包含82种概率分布函数,用来拟合关键掘进参数的概率分布特性,保证了拟合结果的准确性与可靠性,进而能计算出合理且有效的关键掘进参数的控制区间和预警区间。
2 掘进参数对隧洞拱顶沉降显著性分析
2.1 工程背景
陆丰核电站1、2号机组排水隧洞工程位于我国广东汕尾市陆丰市碣石湾,隧洞全长3512.336 m,其中里程SSK0+230.000~SSK3+004.000段采用盾构法掘进开挖,其余部分里程SSK0+000.000~SSK0+230.000(1号排水隧洞)、里程SSK3+004.000~SSK3+512.366(2号排水隧洞)采用矿山法施工。隧洞采用的是6块通用楔形管片方案,管片内径6 700 mm,外径7 400 mm,环宽1 200 mm。隧洞最大、最小埋深分别约为18,12 m。由于埋深与洞径之比变化不大,本研究中不考虑埋深影响,仅分析不同地质条件下掘进参数的取值。核电站1、2号机组排水隧洞平面布置示意如图2所示。
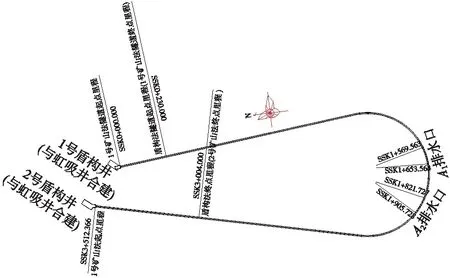
图2 陆丰核电站1、2号机组排水隧洞平面布置示意
核电站1、2号机组排水隧洞盾构施工工程穿越大量不良地层,包括淤泥质土、透水砂层等,各分段区间工程地质情况列于表1,典型区间地质情况如图3所示。由于目前现场盾构施工仅掘进至330环,还未穿越已划分的第一处复合地层,因此本研究仅针对盾构始发段地层(中风化花岗岩、微风化花岗岩交汇的复合地层)进行详细的分析。

表1 分段区间工程地质
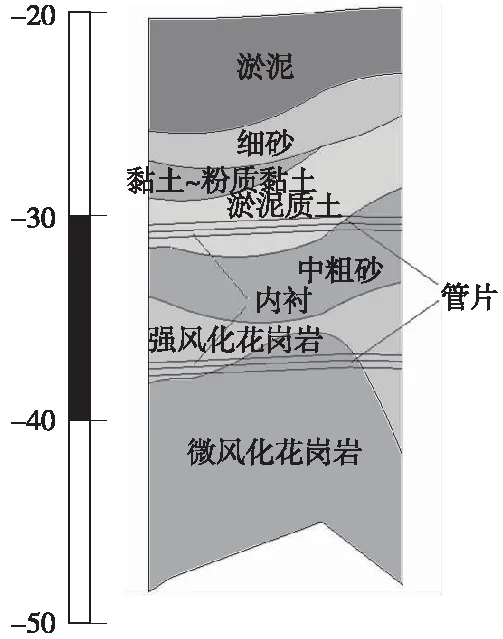
图3 SSK1+451.000~SSK1+513.000区间地质剖面
2.2 基于MIV-BP模型的关键掘进参数评价计算
2.2.1 BP神经网络模型建立与检验
盾构施工过程中的盾构施工效果直接受掘进参数的影响。本工程采用泥水平衡盾构,盾构施工有关掘进参数较多,且每个参数都会受到诸多外界因素的影响。结合本工程中不同复合地层的特点和泥水盾构掘进特性,考虑到本文主要研究掘进参数对不同复合地层的适用性及其控制,故拟选取盾构机总推力、油缸行程差、推进速度、刀盘扭矩、刀盘转速、贯入度、泥水仓泥水压力等13个掘进参数作为BP神经网络的输入参数。另一方面,对于输出参数的选择,许多研究人员[16,20-25]进行了大量的研究,得出盾构施工引起的沉降主要受掘进参数等因素影响的结论,并将沉降值作为神经网络等智能算法的输出参数,构建了盾构施工中反映出掘进参数与沉降值之间映射关系的数学模型。本研究中,由于海底排水隧洞盾构施工工程特殊的环境条件,沉降监测手段有限,因而仅取现场拱顶沉降的实际监测值(该值的选取以盾构机盾尾通过测点位置的累计沉降值为准,此时盾构施工对此位置地层扰动大为降低,引起的拱顶短期沉降基本稳定)作为BP神经网络的输出参数。另外根据经验公式
S=2n+1
(2)
计算出隐含层神经元个数s,n代表输入层节点个数,这里n取13,则s为27,即隐含层神经元个数为27。另外,所建立的BP神经网络模型输入层到隐含层的传递函数选择logsig函数,隐含层到输出层的传递函数选择purelin函数,学习速率设为0.05,迭代次数取10 000,完成BP神经网络模型的建立。
整理现场提供的中风化花岗岩、微风化花岗岩交汇的复合地层(盾构始发段地层)中已经掘进完成的第40~285环资料,获得了154组适用数据。选取144组盾构施工掘进参数的实测数据作为BP神经网络的训练数据,最后剩余的10组数据用于验证所建立的BP神经网络模型的预测精度,BP神经网络预测值与实际监测值的比较详见表2。表2中计算得到的相对误差已控制在较小的范围内,可以看出训练出的掘进参数预测模型较为准确。
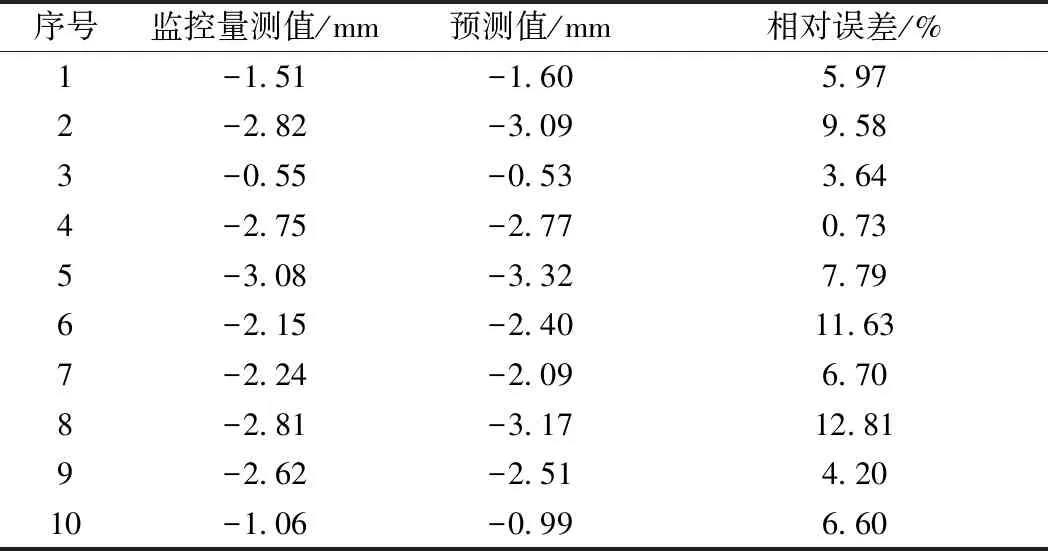
表2 BP神经网络拱顶沉降预测值与实际监控量测值对比分析
2.2.2 MIV评价计算
掘进参数的BP神经网络模型训练完成之后,先将盾构施工掘进参数、隧洞拱顶沉降量的原始观测数据统一进行归一化处理,消除了各变量的单位量纲,再将总推力、刀盘扭矩、刀盘转速、泥水仓泥水压力、油缸行程差等13个掘进参数作为输入参数,利用训练好的BP神经网络模型,分别以10%、15%、20%的MIV调节率,对隧洞拱顶沉降分别进行了154次MIV测试实验,计算结果如表3所示。

表3 不同调节率下掘进参数MIV变化情况
将总推力、刀盘扭矩、刀盘转速、泥水仓泥水压力、油缸行程差、贯入度等13个掘进参数依次编为1~13号影响因子,根据表3中的MIV值分别绘制不同调节率下MIV值变化曲线,如图4所示。
由图4可以看出,在不同MIV调节率下,总推力、刀盘扭矩、泥水仓泥水压力等13个掘进参数对拱顶沉降的影响趋势基本保持不变,同时,根据MIV计算结果显示,刀盘扭矩、总推力、泥水仓泥水压力以及千斤顶铰接压力对应的影响权重值较大,是对隧洞拱顶沉降影响最为显著的关键掘进参数,且总推力、刀盘扭矩与隧洞拱顶沉降量呈正相关,泥水仓泥水压力、千斤顶铰接压力与拱顶沉降量呈负相关。通常情况下总推力、刀盘扭矩规律一致,二者较大会导致盾构机姿态难以控制甚至偏离隧洞设计轴线,造成较大的拱顶沉降量;盾构始发段地层条件较好,土层有自稳能力,较大的泥水仓压力、千斤顶铰接压力能在确保盾构掘进安全的条件下,控制盾构机姿态,从而减小拱顶沉降。因而,适当减少掘进过程中总推力及刀盘扭矩,并提高泥水仓泥水压力、千斤顶铰接压力,可有效控制拱顶沉降,保证施工质量。
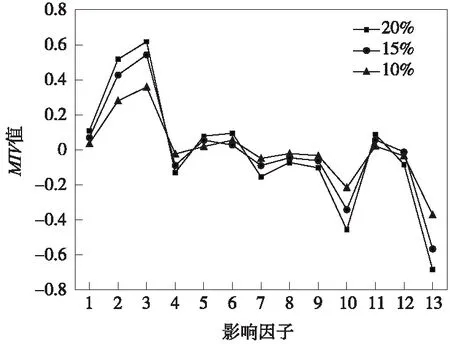
图4 不同调节率下各影响因子对输出参数影响权重变化曲线
3 掘进参数最优分布及其分析
为获得与复合地层相适应的掘进参数取值范围,从而更好地指导海底排水隧洞工程施工,结合目前现场提供的实测数据,对2.2节分析得到的4个关键掘进参数进行统计分析,包括刀盘扭矩、总推力、泥水仓泥水压力以及千斤顶铰接压力。
以刀盘扭矩为例,选取盾构始发段中风化花岗岩、微风化花岗岩交汇的复合地层为基础,利用所开发掘进参数优化分析程序,对目前已经施工完成的、现场提供的第40~285环每环的刀盘扭矩平均值进行统计分析及最优分布拟合,拟合结果如图5、图6所示。可以看出,在中风化花岗岩与微风化花岗岩交汇的复合地层中,刀盘扭矩的最优分布为极值Ⅱ型分布(对应的最小AIC值为0.006 58),同时由样本估计总体,以50%置信水平的置信区间[1.605,1.632] MN·m作为刀盘扭矩取值的控制区间,即在盾构施工过程中,刀盘扭矩值控制在此区间能较好地适应复合地层,减小拱顶沉降量,提高施工质量。以90%置信水平的置信区间[1.586,1.651] MN·m作为刀盘扭矩取值的预警区间,即刀盘扭矩超过此区间,可能会发生较大的拱顶沉降,盾构施工效果较差。
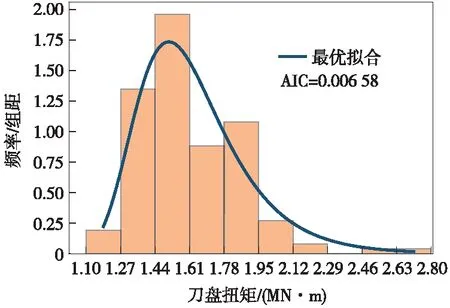
图6 刀盘扭矩数据的最优分布
同理可对其他关键掘进参数做分布拟合和统计分析,总推力、泥水仓泥水压力及千斤顶铰接压力的最优拟合结果如图7所示,所有关键参数的统计分析结果列于表4。

表4 关键掘进参数统计分析结果
注:1 bar=100 kPa。
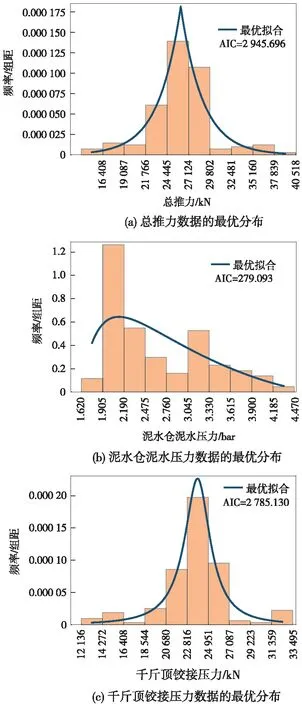
图7 其他关键掘进参数的最优分布
现场盾构始发段地层后续施工(第286~330环管片)的关键掘进参数已采用上述计算得到的50%置信水平下的控制区间进行施工。整理已经掘进完成的第286环之后的资料,共获得15组适用数据,统计出后续施工过程中的隧洞拱顶沉降,管片环缝、纵缝错台量的平均值,管片收敛变形值,并绘制成如图8所示的变化曲线。从图8可以看出,隧洞拱顶沉降,管片收敛变形及管片错台量已控制在较小的范围且基本保持稳定,反映出后续施工盾构效果较好,施工质量较高,所提出的关键掘进参数控制区间及预警区间能有效地指导盾构施工。
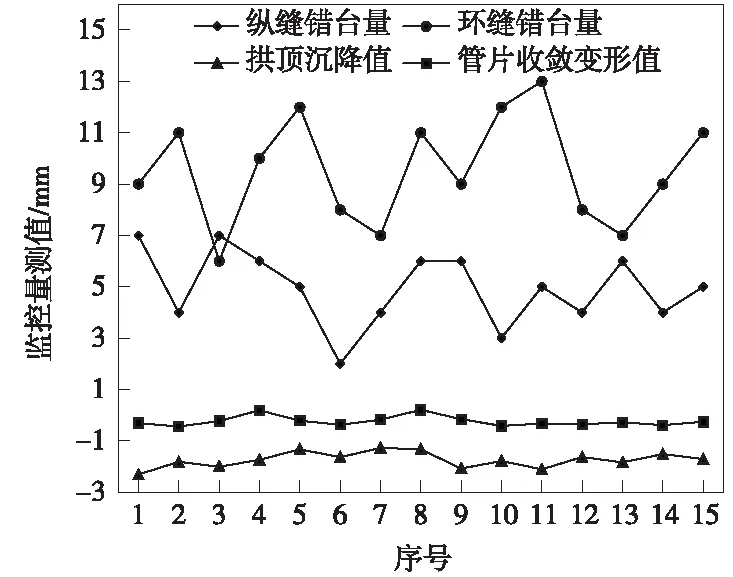
图8 隧洞拱顶沉降、管片收敛变形及管片错台量变化曲线
4 结论
考虑海底排水隧洞盾构施工地层变化频繁、复合交互的工程实际,基于MIV-BP模型、AIC准则的掘进参数选取及最优分布确定方法,提出了以50%和90%置信水平下的置信区间,分别作为掘进参数的控制区间和预警区间的掘进参数优化设计方案,并完成了相应程序的开发工作。通过以上研究,得到以下主要结论。
(1)提出的基于MIV-BP模型的关键掘进参数选择方法,有效的建立了盾构施工过程中掘进参数预测模型,同时依托于掘进参数对隧洞拱顶沉降的影响显著性分析,成功提炼出盾构施工过程中的关键掘进参数:刀盘扭矩、总推力、泥水仓泥水压力、千斤顶铰接压力。
(2)基于AIC准则的关键掘进参数最优分布的确定方法,能准确获得关键掘进参数服从的最优分布,并在此基础上提出的掘进参数控制区间(50%的置信水平)和预警区间(90%的置信水平),规定了相应复合地层下掘进参数的合理取值范围,及时有效指导施工,控制隧洞拱顶沉降。
(3)工程实例的分析表明,本文所开发的掘进参数优化分析程序具有良好的统计分析、快速指导施工的功能,重点考虑了施工现场地层复杂、复合交互的问题,对隧洞拱顶沉降进行了有效的控制,保证施工质量,可以为同类型盾构在相似复合地层下关键掘进参数的选取、优化和隧洞拱顶沉降控制提供施工实时指导。
