局部偏最小二乘法结合可见-近红外光谱预测猪肉挥发性盐基氮

王文秀，彭彦昆*，王 凡，马 营

（1.中国农业大学工学院，国家农产品加工技术装备研发分中心，北京 100083；2.河北农业大学食品科技学院，河北 保定 071000）

我国是猪肉生产和消费大国，2017年猪肉产量达5 340万 t。挥发性盐基氮（total volatile basic nitrogen，TVB-N）是猪肉在贮藏期间蛋白质的分解产物，是反映猪肉是否具有可食用性的重要指标[1]。GB 5009.228—2016《食品中挥发性盐基氮的测定》规定了TVB-N的标准测定方法，但是该方法存在前处理繁琐、耗时长、破坏样品等缺点，无法满足快速、实时、无损伤的检测需要[2]。

近年来，可见-近红外光谱技术与化学计量学结合，已经应用到肉品品质[3-6]、安全[7]、掺假[8-9]、种类识别[10]等研究上，并取得了令人满意的结果。Prevolnik[11]、Prieto[12]、Weeranantanaphan[13]等综述了光谱技术在肉品检测中的应用，表明该技术能够无损检测肉品主要参数。在预测TVB-N方面，Cai Jianrong等[14]基于1 000～2 500 nm之间的近红外光谱，建立了猪肉中TVB-N的偏最小二乘模型，预测相关系数为0.808 4。马世榜等[15]通过特征波长筛选建立了牛肉TVB-N的预测模型，相关系数为0.925 0。上述研究基于校正集样品建立的模型直接预测验证集样品，证实了光谱技术预测TVB-N的可行性。

由于近红外模型建立过程也包括了样品状态、环境变化、仪器条件等因素，因此会出现建立的TVB-N模型在预测不同批次样品时效果不佳的问题，限制了近红外光谱技术在肉品行业的实际应用。为了提高模型的预测能力，Naes等[16]提出了局部回归方法，根据“相似样品产生相似输出”的原理，依据待预测样品的光谱特征，通过某种相似度依据，在数据集样品中寻找部分与之相似的样品，重新建立局部校正模型。该方法可以充分利用原始数据集样品的信息，在土壤全氮含量反演[17]、苹果糖度预测[18]、甜味剂浓度测定[19]等研究中已有应用，但是在猪肉TVB-N检测方面鲜见报道。此外，在建立局部模型时，相似样品选择的依据和数量是至关重要的因素，一些学者对此展开了研究。Dambergs等[20]以待测样品与数据库样品光谱的相关系数作为依据选择局部建模样品，鄢悦等[21]通过光谱信息散度选择样品建立局部校正模型，张红光等[22]利用净信号分析结合欧式距离构建局部模型。这些研究证实了局部建模策略的优势，但是多从单个角度评价不同样品的相似程度，判断能力有待提高。相似度准则的选择仍然是目前需要进一步研究和解决的问题。

为了解决猪肉TVB-N预测模型在应用中面临的上述具体问题，本实验针对两个批次的猪肉实验样品，基于350～2 500 nm波段的可见-近红外反射光谱矩阵，提出了基于距离、信息测度和投影的相似性度量方法，通过构建相似度函数和相似度因子，建立TVB-N的局部偏最小二乘模型，提高模型的预测能力。

1 材料与方法

1.1 材料与试剂

猪肉背最长肌部位购买于北京顺鑫农业股份有限公司鹏程食品分公司、双汇冷鲜肉专卖店以及北京二商大红门肉类食品有限公司。

0.01 mol/L标准盐酸滴定溶液 厦门海标科技有限公司；氧化镁、硼酸、95%乙醇（均为分析纯） 西陇化工股份有限公司；指示剂甲基红和溴甲酚绿 广东光华科技股份有限公司。

1.2 仪器与设备

KDY-9820半自动凯氏定氮仪 北京瑞邦兴业科技有限公司；MYP11-2A磁力搅拌器 上海梅颖浦仪器仪表制造有限公司；5 mL移液枪 德国Eppendorf公司；可见-近红外反射光谱采集系统如图1所示，包括可见-短波近红外光谱仪AvaSpec-2048x14（荷兰Avantes公司）、长波近红外光谱仪AvaSpec-NIR256-2.5（荷兰Avantes公司）、Y型光纤、环形光导、卤钨灯光源等。两台光谱仪的波长范围分别为350～1 100 nm和1 000～2 500 nm，以下分别简称为前波段光谱和后波段光谱。

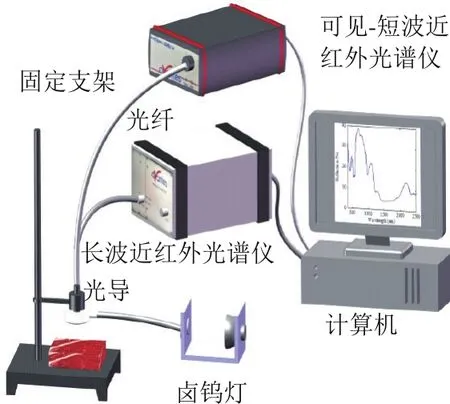
图1 可见-近红外光谱采集系统示意图Fig. 1 Schematic diagram of the visible and near-infrared spectral acquisition system

1.3 方法

1.3.1 样品处理及实验设置

本研究包括两个批次的实验。在第1批实验中，选取屠宰后经过排酸后熟的猪肉背最长肌部位作为样品，去除外层筋膜后，将样品分割为大小约8 cm×5 cm×2.5 cm（长×宽×高）的肉块，放置在自封袋中包好并编号，然后用蓄冷箱运送至中国农业大学工学院无损检测实验室，无积压放置在4 ℃冰箱中保存。共获得有效实验样品108 个，包括鹏程肉40 个，双汇肉38 个，大红门肉30 个。为了增大TVB-N标准参考值的范围，每天从冰箱中随机取出9 个样品用于光谱的采集和TVB-N含量的测定，实验持续12 d。

在第2批实验中，同样以排酸后的猪肉背最长肌部位为样品，包括鹏程肉15 个，双汇肉15 个，大红门肉10 个。样品的前处理方法与第1批实验保持一致，分割包装后置于4 ℃冰箱中保存待用。为了获得不同新鲜程度的样品，每天随机取出4 个样品用于实验，共持续10 d。

上述两个批次的实验在不同的时间进行，第1批次样品用来建立包含多个品种猪肉的校正模型并形成建模基础数据集，第2批次样品用来验证所建模型对不同批次样品的适用性，同时验证提出的局部偏最小二乘建模方法的可靠性。

1.3.2 光谱采集

实验开始前，将样品从冰箱取出并在室温下静置，同时打开仪器进行预热。实验时，首先调节环形光导与标准硫酸钡白板的距离至形成光强均匀无暗影的光斑，确定距离为4 cm。然后，依次采集参比光谱和暗背景光谱进行校准，并在样品表面选取5 个不同位置采集反射光谱信息，平均后作为该样品的最终光谱。

1.3.3 TVB-N理化值测定

参照GB 5009.228—2016方法对TVB-N的标准理化值进行测定。将猪肉绞碎后准确称取（10±0.1）g置于锥形瓶中，加入100 mL蒸馏水搅拌30 min并过滤。然后，准确量取10 mL滤液和10 mL质量浓度为10 g/L的氧化镁溶液，加入到消化管中蒸馏5 min，硼酸吸收液用0.01 mol/L的盐酸标准液进行滴定，根据消耗的盐酸体积计算TVB-N含量。每个样品做3 个平行实验，取平均值作为该样品最终TVB-N值。

1.4 数据分析

1.4.1 双波段数据融合方法

为了更加充分的利用两个光谱仪采集的信息，需要对双波段光谱数据进行融合，以得到连续覆盖整个可见光及近红外区域的光谱曲线。融合方法如下：首先，截掉后波段光谱在1 000～1 074 nm和2 279～2 500 nm范围内噪音较大的光谱数据；然后，保持前波段光谱在350～1 074 nm范围及后波段光谱在1 369～2 279 nm范围的数据不变，利用式（1）对后波段光谱在1 074～1 369 nm范围的数据进行抛物线拟合校正，得到校正后的光谱数据；最后，将350～1 074 nm范围的原始光谱数据、1 074～1 369 nm范围的校正光谱数据以及1 369～2 279 nm范围的原始光谱数据组合形成融合后的光谱矩阵。

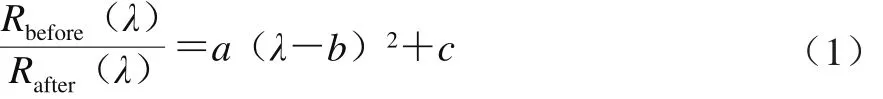
式中：Rbefore（λ）和Rafter（λ）分别为校正前后波长λ位置处的反射率/%；a、b、c分别为抛物线拟合方程的3 个参数。由于1 369 nm为抛物线方程的顶点，因此b和c分别是1 369和1，且为固定值。参数a通过将待融合的前后两个波段光谱在1 074 nm波长处反射率比值代入到式（1）求得。

1.4.2 光谱预处理及建模方法

基于第1批次的实验样品建立TVB-N的预测模型，并利用该模型直接预测第2批次样品，验证模型在不同批次样品之间的适用性。建模前，采用标准正态变量变换（standard normal variate transformation，SNV）对光谱进行预处理，消除散射对光谱的影响[23]。由于两台光谱仪获取的数据间隔不同（分别为0.59 nm和6.80 nm），导致前后两个波段范围的光谱数据个数不同，前波段数据明显多于后波段数据。为了在光谱预处理和建模过程中，两个波段的光谱信息能具有相同的权重，采用“cublic”插值法对融合后光谱以2 nm为间隔进行数据重排。建模采用偏最小二乘（partial least square，PLS）法分析，利用校正集相关系数（correlation coefficient in the calibration set，Rc）、预测集相关系数（correlation coefficient in the prediction set，Rp）、校正集标准分析误差（standard error of calibration，SEC）和验证集标准分析误差（standard error of prediction，SEP）对模型进行评价。

1.4.3 局部偏最小二乘回归模型建立

以第1批次样品为建模基础数据集，建立第2批次样品的局部偏最小二乘回归（locally partial least square，LPLS）模型。建模的步骤包括：首先，确定相似度函数来评价不同样品之间的相似程度；然后，根据相似度函数，在建模基础数据集样品中寻找与待测样品相似的样品，确定局部回归建模邻域窗口；最后，利用局部空间内样品建立待测样品的LPLS模型。各个步骤具体实施过程如下。

1.4.3.1 相似度函数选择

为更加准确全面地衡量光谱之间的相似度，提出基于距离、信息测度和投影的相似性度量方法，分别采用欧式距离、光谱信息散度（spectra information divergence，SID）和光谱角（spectra angle metric，SAM）计算不同样品的相似程度。目前，SID和SAM在高光谱分析中有所应用，但是在近红外分析中应用较少[24-27]。将SID和SAM结合使用，可以从光谱形状和光谱信息熵角度判断相似程度，其计算公式如式（2）所示。同时定义了相似度函数S，对欧氏距离和光谱信息散度-光谱角（spectral information divergence-spectral angle，SID-SAM）进行加权求和，计算公式如（3）所示：

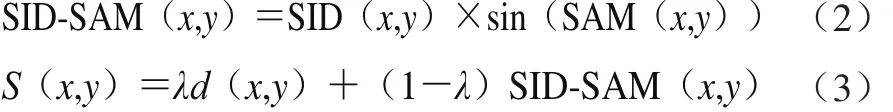
式中：x和y为待分析的两条光谱；d（x, y）为光谱之间的欧式距离；λ为权重因子，取值范围为0～1，当λ为0或1时，表示只计算光谱形状信息或距离。不同样品之间的相似程度越高，d（x, y）和SID-SAM值越小。在计算欧式距离时，将原始光谱矩阵均值中心化后利用主成分分析进行降维，利用得分矩阵代替原始矩阵计算欧式距离。

1.4.3.2 邻域确定

利用式（2）、（3）计算出待测样品与建模基础集中各样品的相似度后，将样品按相似性从大到小排序，依次选择样品组成邻域窗口h。为了提高确定窗口h的效率，定义相似度因子SM，其计算公式如式（4）所示，其中Mmax为建立LPLS模型的最大样品数，为经验值，M为实际建模的样品数，介于1和Mmax之间。相似度因子SM可理解为窗口h内样品的相似度总和在最大LPLS建模样品相似度总和中的比重，可通过代价函数（式（5））计算确定，代价函数最小时的SM为LPLS建模时的SM。

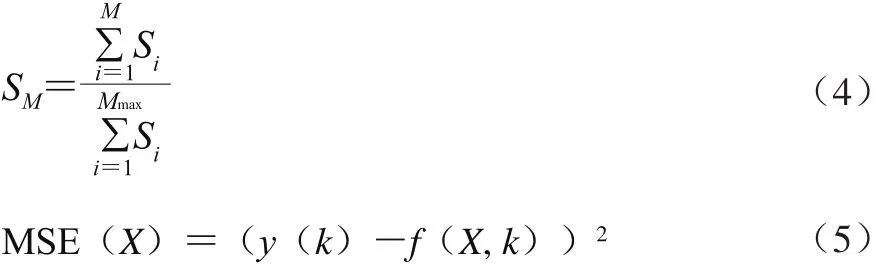
式中：Si为待测样品与排序后建模集第i个样品的相似度；X为建立LPLS模型的样品组成的子集；MSE为对外部验证样品的预测误差；y（k）为第k个样品的标准参考值；f（X, k）为LPLS模型对该样品的预测值。

1.4.3.3 LPLS模型建立

结合实验数据对参数λ和SM寻优，确定最佳取值后，可确定每个待测样品LPLS模型的建模样品。然后，利用竞争性自适应重加权采样（competitive adaptive reweighted sampling，CARS）算法实时优选特征波长，并基于特征波长下的光谱建立LPLS模型。最佳潜变量数通过留一法交叉验证确定，分析流程如图2所示，分析过程在Matlab2012a中进行。

图2 LPLS模型分析流程图Fig. 2 Flow chart of local partial least squares analysis

2 结果与分析

2.1 原始光谱和TVB-N参考值分析

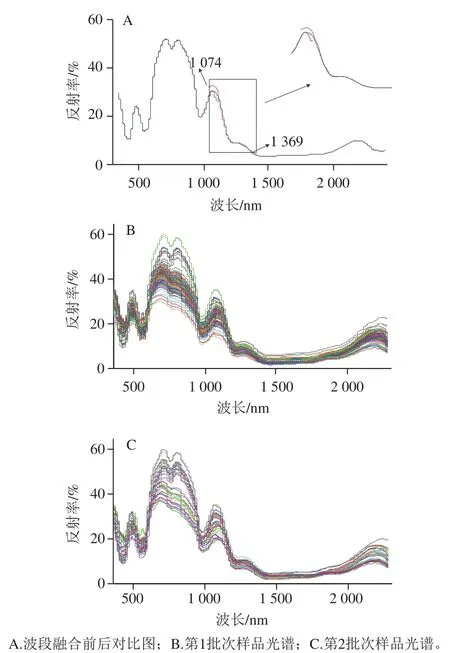
图3 实验样品的原始光谱Fig. 3 Original spectra of experimental samples

获得两个波段的光谱数据后，首先利用抛物线拟合法对双波段数据进行融合，对某个样品连接前后的光谱对比图如图3A所示。从融合前的双波段光谱（前波段为350～1 100 nm，后波段为1 074～2 279 nm）可以看出，在1 074～1 100 nm波段范围内，由于仪器响应不同，两台光谱仪获取的光谱数据并不一致。而利用抛物线拟合法进行校正后，两段光谱可以有效的融合为一条连续无陡变的光谱。融合后的两个批次样品的原始光谱图如图3B和3C所示，其中545 nm为肌红蛋白的吸收峰，980 nm为O—H键的吸收峰，1 280 nm与N—H键振动有关，2 200 nm与C—H键振动有关[28-30]。对比图3B和C，可以看到不同批次实验样品的光谱趋势基本一致，仅在光谱强度上有所差异。针对一个批次样品的光谱来看，在630～925 nm波段范围之间，不同样品的光谱存在差异，这可能与样品品种和来源不同有关。

2 个批次实验样品的标准参考值统计信息如表1所示，TVB-N含量范围分别为7.49～44.17 mg/100 g和8.17～39.54 mg/100 g。根据GB 2707—2016《鲜（冻）畜、禽产品》的规定，TVB-N含量小于15 mg/100 g时样品为新鲜肉，可见2 次实验均涵盖了新鲜和腐败的样品，且第1次实验的理化值范围大于第2次实验。

表1 2 个批次实验样品的TVB-N含量统计信息Table 1 Descriptive statistics of TVB-N contents in the two sets of samples mg/100 g

2.2 第1批次样品建模结果分析

对第1批实验样品的双波段光谱进行数据融合且重排后，利用SNV对光谱进行预处理。然后以3∶1的比例对108 个样品进行分组，则有80 个样品组成校正集建立模型，28 个样品组成验证集对模型进行验证。建立的PLS模型预测性能较好，Rc和Rp分别为0.952 0和0.940 8，SEC和SEP分别为2.286 5 mg/100 g和2.442 4 mg/100 g。

2.3 直接预测第2批次样品结果分析

利用2.2节中建立的PLS模型直接预测第2批实验样品，验证所建立的模型对不同批次样品的适用性。在进行模型验证时，同样需要对第2批样品的光谱进行双波段数据融合，并以2 nm为间隔进行数据重排。进行SNV预处理后，将光谱矩阵与2.2节建立的模型系数矩阵相乘可以得到预测值，第2批40 个样品的真实值与预测值散点图如图4所示。

从图4可以直观地看出，一些样品的预测效果不理想，真实值和预测值的偏差较大，总体相关系数R为0.845 6，SEP为4.581 0 mg/100 g。这表明不同批次实验样品之间存在差异，利用建立的模型直接预测不同样品时容易产生较大的误差，模型的适用性需要进一步增强。

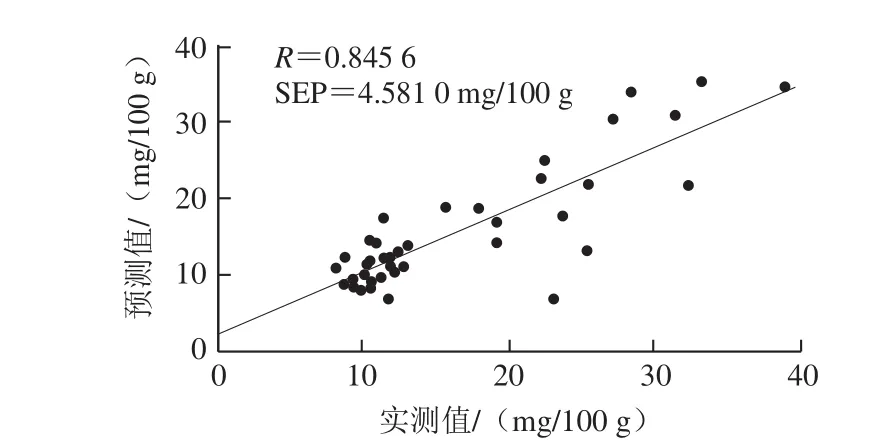
图4 直接预测第2批次样品时真实值和预测值散点图Fig. 4 Comparison between actual values and predicted values of the second batch of samples using the established model

2.4 LPLS模型预测第2批次样品结果分析

由于直接利用第1批样品建立的模型预测第2批样品时，预测结果有待提高，因此进一步考察LPLS模型的预测效果。以第1批样品为建模基础数据集，计算第2批样品与其中每个样品的欧式距离和SID-SAM值。从图3可以看出，不同来源的样品光谱存在差异，为了消除这种差异对求取欧式距离和SID-SAM值的影响，在计算之前对两批样品进行极差归一化预处理，使光谱处在一个相同的数据范围内。具体方法为：将样品的光谱数据看作是p元行向量（p为变量数），将该行的每一个数据与最小值求差，然后除以该行数据中最大值和最小值的差。经过处理后的两批实验样品光谱曲线如图5所示，红色和蓝色分别为第1批和第2批实验样品的光谱。可见数据都映射到0～1之间，各个变量和平均值分布更加均衡，光谱间无明显差异，有利于后续的计算和分析。

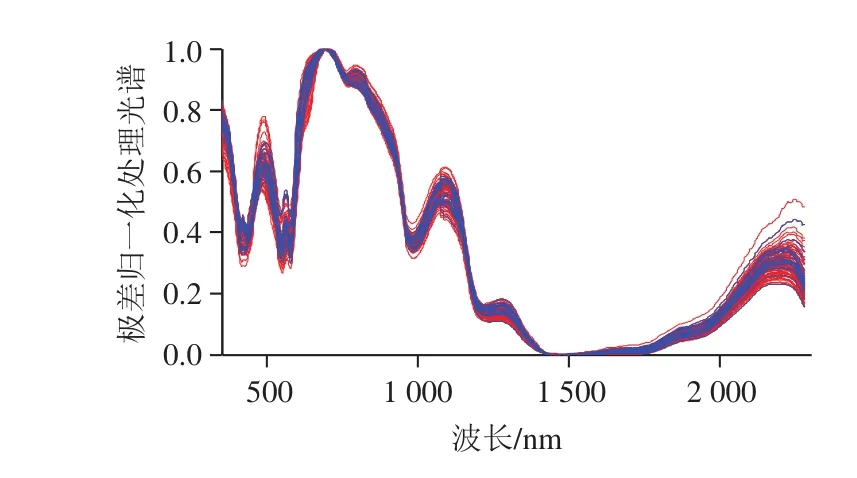
图5 极差归一化处理后两个批次样品的光谱Fig. 5 Normalization pretreated spectra of the two batches of samples

在建立LPLS预测模型，不同的λ和SM取值会获得不同的邻域，进而得到不同的预测结果，因此需要对这两个参数进行寻优以确定最佳取值。在计算相似度时，由于距离对光谱差异的影响大于形状和角度，因此赋予距离更大的权重，设定λ的取值分别为0.5、0.6、0.7、0.8、0.9和1.0。SM的取值直接影响建立局部模型的窗口大小，取值太大，会导致建立LPLS模型的样品数太多，影响模型的准确性及实时建模的速度和效率；若取值太小，会导致选择的样品数过少，不能准确反映光谱特征与标准参考值之间的关系。在计算出待测样品与建模基础数据集中每个样品的相似度后，将样品按相似性从大到小排序。根据经验值设定Mmax为40，即建立LPLS模型的最大样品数量为40，计算出前40 个样品的相似度总和。然后设定SM分别为0.50、0.55、0.60、0.65、0.70、0.75、0.80、0.85、0.90、0.95和1.00，共11 个取值。结合λ的6 个取值，可以得到66 种λ和SM组合，因此对于第2批实验中的每一个样品，可以建立66 个LPLS预测模型，进而得到66 个预测误差。对每种组合下第2批40 个样品的预测误差求平均，比较66 种组合下的平均误差值，通过最小化该误差值，确定λ和SM的最佳组合。经过比较分析，在欧式距离和SID-SAM的权重分别为0.8和0.2，相似度因子SM为0.8时，第2批40 个样品的平均预测误差最小，因此确定0.8为λ和SM两个参数的最优值。

根据图2的数据分析流程，在λ和SM值确定后，分别得到第2批40 个样品的建模邻域窗口，利用CARS算法实时优选特征变量，并建立LPLS预测模型，真实值与预测值的散点图如图6所示。与图5中直接预测的结果相比，模型效果有了明显的改善，预测相关系数R上升至0.948 1，SEP下降至2.650 8 mg/100 g。利用显著性检验方法对真实值和预测值进行统计学分析可知，P＞0.05，表明两组数据无显著性差异。这也说明利用LPLS方法建模，能有效提高对外部验证样品的预测能力。

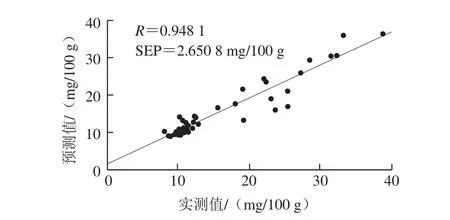
图6 采用局部建模方法对第2批次样品预测结果Fig. 6 Prediction results for the second batch of samples using LPLS

本研究结合欧式距离和SID-SAM，可以更加综合全面地评价不同光谱之间的相似性，更有利于找寻与待测样品光谱特征相似的建模样品。通过优化SM值，对每一个待测样品，均能从建模基础数据集样品中动态选择最佳建模邻域窗口。相比在建立LPLS模型时，根据待测样品的光谱特征，在基础数据中以待测样品为中心搜索固定距离空间内的样品，或搜寻与之相似性较高的固定个数的样品，该方法具有更高的灵活性，可根据样品特性实时优选出最佳建模用样品子集。在整个分析过程中，确立邻域空间和建立模型都是根据样品“需要”判断后自动进行，具有较强的自适应学习能力。与利用模型直接预测不同批次样品的结果相比，LPLS方法具有更高的灵活性和适应性，尤其对于样品差异较大引起非线性问题时，LPLS方法比全局PLS方法对样品的预测能力更佳。

3 结 论

针对光谱法检测猪肉TVB-N时，建立的校正模型对不同批次实验样品预测效果不佳的问题，提出了局部偏最小二乘法预测TVB-N含量的方法。计算外部验证样品与建模基础数据集中所有样品的欧式距离和SID-SAM，以权重分别为0.8和0.2对二者进行加权求和，计算出相似度函数。以相似度因子为0.8选择建模邻域，对外部验证的每一个样品构建LPLS预测模型。与利用校正模型直接预测外部验证样品时的结果相比，LPLS模型具有更大的预测能力，相关系数R从0.845 6上升至0.948 1，SEP从4.581 0 mg/100 g下降至2.650 8 mg/100 g。在今后的研究中，收集更多品种和来源的样品组成建模基础数据集，结合本研究的方法，可以实现对更多样品的无损预测。此外，也可将该方法应用于利用可见-近红外光谱法预测猪肉其他参数的研究中。