磁轴承滑模控制研究综述

鞠金涛，朱熀秋，许泽刚，谷超，张寰

(1.常州工学院 电气信息工程学院，江苏 常州 213032；2.江苏大学 电气信息工程学院，江苏 镇江 212013)

磁悬浮轴承(简称磁轴承)是一种新型无接触轴承，能够解决传统机械轴承摩擦导致磨损大，寿命短，润滑油污染，不易密封等问题，特别适用于高速、高精度、真空、超洁净等场合。随着工业要求的不断提高以及磁悬浮技术的不断发展，磁轴承已经充分突显其在传动支承部件中的优势。

磁轴承关键技术包括：定转子材料研究，结构形式研究，参数设计与优化，控制方法研究,数字控制系统研究,无传感器技术研究等。其中，决定磁轴承性能的核心技术是针对其系统参数不确定、各种内部和外部扰动、耦合等非线性特性的控制方法[1]。目前，磁轴承的控制主要包括：PID控制[2]、模糊控制[3]、H_∞控制[4]、滑模控制[5]、自抗扰控制[6]、模型参考自适应控制[7]、预测控制[8]、神经网络控制[9]，以及对这些控制方法的改进、结合而构成的新型控制方法。

上述控制方法大部分根据磁轴承近似线性化后的数学模型设计控制器，而磁轴承的固有非线性比较强，此类控制器不能在磁轴承的全工作范围内取得较好的效果。虽然滑模控制也是基于磁轴承在平衡点线性化后的数学模型所设计，但可以将磁轴承模型的非线性看作系统参数的摄动，将转子不平衡、各自由度间的耦合等不确定的扰动当成系统外部扰动，从而将磁轴承的控制性能归结于处理控制系统的鲁棒性问题。由于滑模控制在非线性控制系统中鲁棒性强，易于物理实现，响应快，在磁轴承控制领域得到了广泛关注。现综述滑模控制在磁轴承研究中的国内外现状，总结滑模控制在磁轴承中的应用方式，分析滑模控制在磁轴承中应用研究的发展趋势。

通过对先秦时期音乐思想的浅析与对比，在现如今音乐思想文化迅速发展的时期，音乐艺术的价值取向、审美的境界，应该重新审视与整理。音乐文化需要发展，需要有时代特征与独特魅力。希望我们的音乐创造者能够以一定的等级和标准创造出更多的能经受时代考验的音乐艺术作品！

1 磁轴承滑模控制研究现状

1.1 国外研究现状

1996年，文献[10]将滑模控制应用于垂直轴的磁轴承系统，首先将非线性模型进行线性化处理，建立关于转子质量中心的旋转动力学方程。由于将非线性模型进行了线性化处理，因此模型参数具有不确定性，并且由于转子不平衡引起的正弦扰动，要求设计的控制器必须具备较强的鲁棒性。滑模控制器的强鲁棒控制特性使系统受到参数摄动和外部扰动的影响较小，因此设计了滑模控制器实现磁轴承的稳定运行和转子位置跟踪能力；并且设计了滑模观测器，在系统出现未匹配的扰动时，通过对测量信号导数的不连续近似滤波来估计系统状态和干扰，为今后实现转子自平衡奠定了基础。

1998年，文献[11]在平衡位置线性化的磁轴承数学模型基础上，考虑转子陀螺效应和不平衡扰动，将陀螺效应惯量矩阵和不平衡扰动矩阵中的参数用转速的函数表示，从而将主动磁轴承看作一个线性参数变化系统。结合鲁棒控制针对线性时变系统所采用的增益调整思想，设计了滑模控制器的时变滑模面，该滑模面为一个线性矩阵不等式，由于基于线性参数变化系统进行设计，可根据转速连续变化，从而保证了不同转速下系统的稳定性和跟踪性能，有效抑制了与转速相关的陀螺效应和转子不平衡对系统所产生的影响。其控制框图如图1所示，其中K为控制器；P为磁轴承系统模型。

图1 磁轴承系统时变超平面滑模控制框图

2001年，文献[12]针对磁悬浮平衡梁系统参数变化和外部扰动的问题设计了积分滑模控制器，其控制框图如图2所示。首先,对磁悬浮平衡梁系统的数学模型进行线性化处理;然后,设计了一个积分控制器，以积分控制器的输出、转轴偏转角度、角速度及控制电流作为状态变量设计滑模切换面。设计的滑模控制器输出包含线性分量和非线性分量2个部分，线性控制分量由滑模面的一阶导数为零计算得到，非线性控制分量采用一个带边界层的连续趋近律来减小系统颤振。该控制方法利用积分补偿消除了稳态误差，并通过仿真和试验证明该方法在外部干扰和输入信道参数变化影响下仍然具有较好的效果。2003年，文献[13]将该控制方法应用于一个永磁偏置磁轴承支承的人工心脏泵系统。

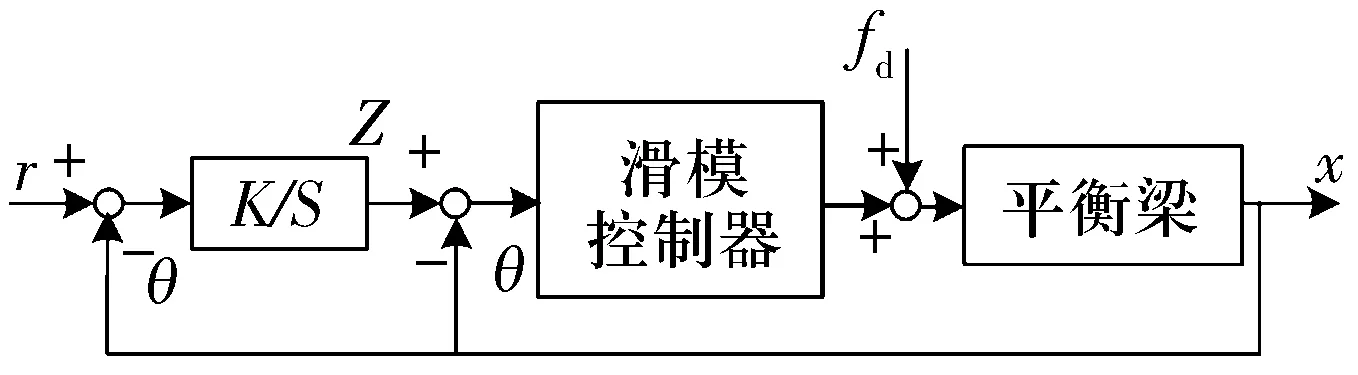
图2 磁悬浮平衡梁系统积分滑模控制框图

2016年，为了使控制器对参数不确定和外部扰动具有较强的鲁棒性，文献[19]根据磁悬浮球系统的非线性动态特性，针对电流环采用基于扰动观测器的滑模控制器控制，针对位移环设计了基于系统状态和扰动观测器的滑模控制器，系统状态扰动观测器用来估测整个系统的状态量与不确定性，该方法克服了传统滑模控制不确定边界和扰动必须预知，不连续控制导致过度偏移，状态向量能完全被测的缺点。首先，建立电气环的数学模型，即控制电压和控制电流方程；然后，建立机电模型，模型中悬浮力与控制电流的平方成正比，与小球位移的平方成反比；最后，基于悬浮力表达式以转子位移、位移一阶导数及控制电流作为状态变量，控制电压作为输入变量，建立系统非线性状态方程。在设定控制目标时，将系统目标误差中的非线性和不确定部分写成线性误差的不确定性项。由于控制器中需要转子位移的一阶导数，采用数字求导会导致系统延时也可能放大测量噪声，因此设计了状态扰动观测器估测系统状态和扰动。以转子位移及其导数误差作为状态变量，控制电流作为输入变量建立状态扰动观测器的系统状态方程，通过选取合适的位移误差增益和扰动增益能够保证观测器的估算方程位于左半相平面。分别针对位移误差和电流误差设计滑模控制律。采用Lyapunov函数证明了该控制系统的稳定性，并与LQR+PI控制器进行仿真和试验对比，证明了其具有较好的鲁棒性，控制系统框图如图5所示。

2010年，文献[15]针对电压控制型三极主动磁轴承设计了二阶积分滑模控制器。首先，将状态变量分为动力学状态变量部分和磁通状态变量部分，并将磁通状态变量部分看作动力学状态变量部分的输入，则数学模型降维成非仿射的非线性系统；然后，利用反馈线性化方法将系统数学模型变为线性系统，并针对线性系统设计了滑模控制器，作为外环的第2阶滑模控制器；最后，针对磁通状态变量设计内环滑模控制器，从而构成了二阶积分滑模控制器。仿真和试验结果表明，所设计的控制器在系统参数变化40%时仍能很好地跟踪给定位置信号，调节时间0.5 s，稳态精度15 μm。三极主动磁轴承试验平台如图3所示。

图3 三极主动磁轴承控制系统试验平台

2011年，文献[16]采用智能双积分滑模控制系统实现五自由度主动磁轴承的悬浮，控制系统框图如图4所示。五自由度主动磁轴承系统是一个高度非线性时变系统，系统参数的变化、外部扰动、五自由度之间的耦合、陀螺效应等使系统的5个自由度的位移受到不止一个力的影响，为了实现分散控制，先将五自由度主动磁轴承系统解耦为5个独立的子系统，分别设计控制器。双积分滑模控制器是在设计滑模面时加入系统误差的二次积分项来进一步消除系统稳态误差，但引入积分项可能会导致控制器的饱和，因此双积分滑模控制器6个控制参数的全局设计较难。该方法通过改进的神经网络观测器实现控制器增益参数的自适应调节和系统不确定性观测，观测器的最优输出作为观测目标。与积分滑模控制相比，该控制方法采用双积分滑模面进一步消除稳态误差，改进的PID神经网络观测器通过自适应的PID控制增益和在线不确定性观测能力增强了控制律，并且不需要估算整个系统的不确定性边界，因此这种方法同时具备积分滑模控制、自适应控制和神经网络控制的优点。

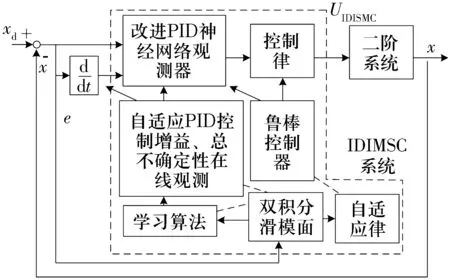
图4 智能双积分滑模控制系统框图

文献[17]研究了用非奇异终端滑模控制实现非线性推力主动磁轴承轴向位置的有限时间跟踪控制。首先将轴向磁轴承的悬浮力数学模型在平衡工作点进行线性化，然后将动力学方程分离成名义系统和系统总不确定性2个部分，后者的边界需要进行估算，作为趋近率的增益。根据系统误差方程设计终端滑模面，终端滑模控制器的输出要满足使终端滑模存在的充要条件，系统误差到达滑模面的时间也要控制在有限范围内。考虑到终端滑模控制器可能存在奇异问题：当系统误差为0，系统误差导数不为0时，不能保证控制变量为有界值，因此把终端滑模面改为非奇异的终端滑模面。但由于系统的高非线性及时变性，系统不确定性的边界很难确定，因此设计了2输入1输出的递归赫米特神经网络在线估测系统不确定性边界。该网络不同隐含层神经元具有不同激励函数，具有出色的时域动态仿射，并对未建模动态、参数变化和外部扰动具有良好的控制性能。由于利用神经网络估计系统不确定性，不再需要切换函数或者饱和函数，因此系统不存在颤振且能保持渐近稳定性。试验结果表明该控制器能很好地跟踪各种给定轨迹。

2018年，文献[21]将转子不平衡振动当成谐波扰动处理，针对转速大范围变化下转子不平衡的时变性，提出了二阶滑模控制方法，该方法包括稳定系统的线性PID控制器以及消除模型不确定性和外部谐波扰动的二阶滑模控制2个部分。首先，采用Taylor展开线性化的悬浮力数学模型建立系统状态方程，外部扰动主要考虑转子不平衡力；然后，设计二阶滑模控制器，不仅要保证传统滑模面为0，并且要保证滑模面的一阶导数为0，即系统到达滑模面后的速度为0，这样就避免了颤振问题。分别设计了螺旋算法、基于数字求导的次优算法和基于高增益观测器的次优算法3种二阶滑模控制器。通过对3种控制器进行仿真和试验分析可知，在全转速范围内，螺旋算法二阶滑模控制器效果最优，与PID控制器单独控制相比，振幅减小50.76%。该研究的创新之处在于：1)提出了二阶滑模控制法作为PID控制增强扰动抑制能力的附加控制；2)针对变转速主动磁轴承实现了螺旋和次优二阶滑模控制算法的应用；3)在实际的平台上实现了该控制方法；4)对参数调好的PID控制器和带二阶滑模控制的PID控制器进行了公平的比较分析；5)推导出二阶滑模控制方法在有效处理谐波干扰时带宽受限的条件。

化工工业园区的发展离不开严格的安全环保管理制度。据工业区发展有限公司董事长孙莉军介绍，几年前，工业区曾为化工企业产生的废气废水扰民、污染环境而深感头痛。通过3年环境综合整治，工业区关停了44家小化工企业，使经济发展和环境质量改善呈现两升三降的良好态势，即工业产值年均增长21%，税收年均增长17%；环境信访量年均下降36%，万元产值能耗年均下降13%，区域VOCs排放量比2016年下降17.6%。经过艰辛努力，通过执行一整套行之有效的管理制度，一定程度上解决了长期困扰工业区发展的环境问题。“对于化工园区来说，安全环保永远在路上。”孙莉军如是说。

文献[33]针对磁悬浮轴承对风力发电机的转子不平衡扰动问题，设计了滑模扰动观测器来观测磁轴承转子不平衡引起的扰动。首先，以转子重心转角速度、倾角角速度和转子位移作为状态变量，建立考虑转子不平衡扰动的系统状态方程；然后，根据降维观测理论将系统分为角速度部分和输出部分，根据降维后的方程设计滑模扰动观测器，利用系统的输入和输出观测系统状态变量；最后，利用观测器观测到的误差对不平衡力矩和绕动力进行补偿，其控制系统框图如图14所示。仿真结果表明，该滑模观测器能够很好地跟踪扰动，使系统扰动降低了90%，有效抑制系统的不平衡扰动。

2014年，文献[18]针对强非线性三极主动磁轴承的稳定悬浮，比较了分散PID控制器和积分滑模控制器的控制性能。首先基于Taylor展开建立了悬浮力的线性化模型，以转子位移及其一阶导数，控制电流及其一阶导数作为状态变量建立系统状态方程，设计了转子位移和电流的PID控制器，该控制器包括位移状态变量的比例、微分积分项和电流状态变量的比例、微分项，利用线性二次最优控制率确定系统的反馈增益。由于控制器中有电流状态变量的PD项，采用霍尔传感器检测到的电流信号易受较大的噪声干扰，如果采用滤波器会因系统延迟而不稳定，因此采用Kalman滤波器估算转子位移的导数、电流信号及其导数。然后分析了系统的非线性模型，为了设计滑模控制器，采用输入/输出线性化法将系统变为标准典范形式，即对系统输出求导直到显含输入变量。当求到位移的四阶导数时才出现输入量，因此设计的积分滑模面包括输出变量及其一至三阶导数。采用极点配置法确定滑模面各项系数，并用Lyapunov函数分析保证系统稳定下滑模面切换项系数的限制条件。通过对2种控制方法的试验分析可知，带Kalman观测器的PID控制反馈控制律简单，计算时间短，对系统的不确定性不敏感，因此具有较强的鲁棒性。

如果有，临床微生物实验室应向医生提供当地医院和工作地区使用的抗菌药体外药敏试验结果的累积报告，作为描述医院和社区获得性病原体敏感性的定期报告。这些报告应有助于医生选择治疗用的抗菌药物。

2005年，文献[14]针对非线性极强的三极主动磁轴承设计了3种控制器：线性状态反馈控制器、反馈线性化的线性状态反馈控制器和反馈线性化的积分滑模控制器。由于三极磁轴承的各个磁极之间存在耦合，加上悬浮力和磁场的非线性，在设计积分滑模控制器前利用反馈线性化方法对三极磁轴承的输入变量进行变换，得到新的输入变量，三极磁轴承的数学模型在该变量下被解耦和线性化，成为线性模型。对设计滑模控制器参数时所需的不确定边界进行了理论分析，针对反馈线性化的数学模型设计了积分滑模控制器。试验结果表明，积分滑模控制器在转子转动下的瞬态和静态控制效果最好，但随着转速的上升，系统振幅也随之增大。

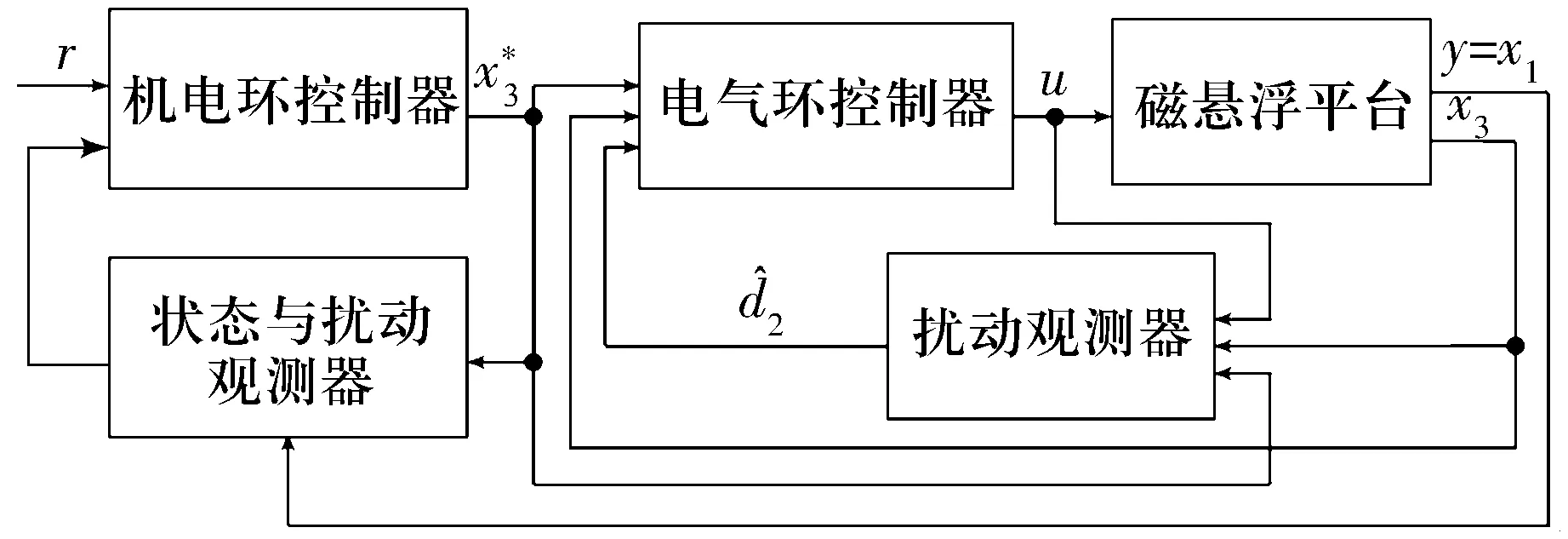
图5 基于扰动观测器的滑模控制系统框图

2017年，文献[20]为了解决轴向主动磁轴承系统外部扰动问题，提出了一种PID模糊滑模控制，如图6所示。基于Taylor展开的线性化数学模型建立系统状态方程，将参数不确定性和扰动统一为总不确定性，从而得到标准滑模形式的状态方程。首先设计一个传统PID控制器，然后设计了PID面滑模控制器，采用类似于PID方程的滑模面，即滑模面包括输出变量的比例、积分、微分项，用饱和函数作为切换函数。为了减小颤振，用模糊算法对饱和函数进一步滤波，选取饱和函数值作为模糊规则的输入，电流补偿量作为模糊规则的输出设计模糊规则，输出函数采用线性函数。最终控制电流由PID控制器、PID面滑模控制器和模糊补偿电流三部分控制信号叠加得到。在没有扰动和有扰动情况下与鲁棒非奇异终端滑模控制方法进行对比分析，仿真和试验结果表明该控制方法具有很好的跟踪性能和稳态精度。

首先，人民检察院在审查起诉过程中听取值班律师的意见并不等于值班律师真正参与了“控辩协商”过程，人民检察院仅仅是“听取”值班律师的意见，至于意见究竟是否一定被采纳、在多大程度上采纳从《试点办法》中无从得知。在这一过程中值班律师更多的是充当“检察官助理”的角色，帮助检察官完善对犯罪嫌疑人的审查起诉。同时，《试点办法》对检察官具体如何听取值班律师和犯罪嫌疑人的意见也没有明确的规定，这就意味着检察官听取犯罪嫌疑人和值班律师的意见可以采取“背靠背”的方式分别听取他们的意见。这样，犯罪嫌疑人在缺少值班律师现场帮助的情况下，其如何能够提出有效的自我辩护意见呢?

图6 PID模糊滑模控制系统框图

1.学生对学习认识上的偏差。对发现知识、了解知识、掌握和运用知识的难度估计不足或认识不深，以为轻而易举，结果一旦遇到困难便知难而退。缺乏对学习难度充分认识的心理准备，由此滋生厌学情绪。

浓重不可分解的悲酸，使树叶垂头。赵三在红蜡烛前用力敲了桌子两下，人们一起哭向苍天了！人们一起向苍天哭泣。大群的人起着号啕！

文献[22]研究了由轴向主动磁轴承和2个径向被动磁轴承构成的五自由度磁悬浮系统，由于径向被动磁轴承会对轴向磁轴承产生外扰力，增强轴向主动磁轴承的系统非线性和时变性，因此设计了基于径向基网络的自适应滑模控制器。利用Taylor展开公式建立了轴向主动磁轴承的近似线性数学模型，根据线性数学模型设计了滑模控制器。为了应对系统的不断变化，采用径向基网络精确估算滑模控制器中的系统不确定性和扰动参数，该网络以转子位移误差及其一阶导数作为网络输入，以系统不确定性和扰动作为网络输出。选取Lyapunov函数对系统稳定性进行分析，包括滑模面函数的平方和径向基网络权值矩阵误差的平方2个部分。设计了自适应律在线调节网络权值学习速率参数，学习速率低能保证系统渐进稳定性，但影响效率；学习速率高会引起振荡甚至不稳定。通过对建立的Lyapunov函数进行分析得出保证系统稳定下的参数选择范围。控制系统整体框图如图7所示。由于设计的测试平台转轴的1阶和2阶临界频率较低，因此仅在1 890 r/min转速下进行试验分析，结果表明，所提出的自适应滑模控制器具有较好的跟踪性能和抗扰动鲁棒性能。

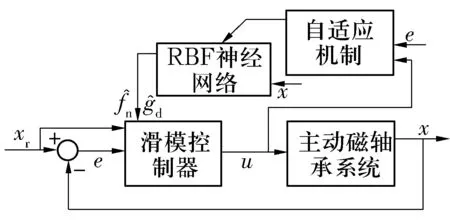
图7 自适应滑模控制系统框图

1.2 国内研究现状

2008年，文献[23]采用多输入多输出积分滑模变结构控制解决四自由度磁轴承系统在模型摄动或外部干扰时出现的转子位置静态误差大、鲁棒性差等问题。首先，基于线性化数学模型建立四自由度磁悬浮轴承系统状态方程，在设计积分滑模控制器时将转轴沿轴向旋转引起的偏心力视为系统模型摄动；然后，选取4输入4输出系统的积分滑模面，求得积分滑模等效控制率以及切换控制律；最后，设计控制器具体参数，使系统满足稳定性判据条件，并对闭环极点进行合理配置。控制系统仿真分析的结构框图如图8所示，结果表明，与自由梯阶滑模控制相比，积分滑模控制的静态误差较小，转速变化引起的系统参数摄动不敏感，对周期性的高频干扰和脉冲干扰具有良好的鲁棒性，响应时间短，并且没有抖振现象。

图8 多输入多输出滑模控制仿真框图

2009年，文献[24]针对飞轮转子系统非线性和不确定性设计了滑模控制器。在建立系统状态方程时考虑了转轴的陀螺效应，并对状态方程进行了量纲一化处理，由于系统方程是简约型，因此可将系统方程分成一阶运动方程和二阶运动方程，将一阶方程作为滑模运动动力学方程，利用Lyapunov方法建立滑模面，然后设计了采用比例趋近律的滑模控制器，分析了各个控制器参数对系统性能的影响。仿真表明，系统的动态响应较快，稳定精度较高，抖振在允许范围内。但仿真过程中，控制器参数不能同时满足系统的鲁棒性和较小的高频抖振，要达到控制性能最优，还需将滑模控制与其他控制方法相结合。

2010年，文献[25]针对磁悬浮反作用飞轮提出了一种离散滑模控制方法解决系统的不平衡量和非线性干扰，为抑制抖振，采用模糊控制器输出的绝对值来对控制系统的增益进行自适应调节，并设计了离散非线性跟踪微分器用于合理提取位移微分信号，代替实际速度信号实现全状态反馈。仿真结果表明，该控制方法在加入不平衡和非线性干扰后仍能够快速回到平衡位置，基本没有超调，控制电流出现少许起伏，但抖振得到了有效抑制，该控制系统框图如图9所示。

图9 离散模糊自适应滑模控制系统框图

2012年，文献[26]针对磁悬浮控制力矩陀螺转子不平衡振动产生的同频扰动，提出了基于滑模变结构扰动观测器的振动抑制控制方法。建立了不平衡扰动和力矩作用下的系统模型，该方法利用滑模控制方法构造系统扰动观测器，对系统扰动和力矩进行在线观测，并利用跟踪微分器估计转子运动的速度信号，以此降低观测器阶数，利用观测到的扰动量对惯性主轴位置进行校正，控制系统框图如图10所示。仿真和试验结果表明，该控制方法能够减小72%的同频振动，有效抑制系统不平衡振动。

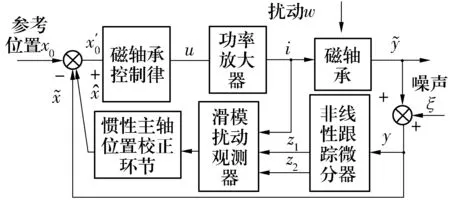
图10 基于滑模扰动观测器振动抑制控制系统框图

文献[27]针对磁轴承系统结构参数的时变性和非线性，结合了滑模控制与自适应控制的优点，设计了一种自适应滑模控制器。设计时引入了自适应估测的系统状态变量矩阵和输入变量矩阵参数，通过自适应律实时估测系统参数变化，改变滑模控制器的控制律，选用饱和函数作为切换控制律，通过定义Lyapunov函数设计自适应控制律，保证控制器设计的稳定性。仿真和试验结果表明，该控制方法能够实现磁轴承的稳定悬浮，并且对外部扰动具有较好的鲁棒性。

2014年，文献[28]将α阶逆系统与滑模控制器相结合，实现磁悬浮控制力矩陀螺的非线性和强陀螺效应的解耦控制。建立了磁悬浮控制力矩陀螺的非线性动力学方程，分析了各个自由度之间的耦合特性，当系统转速较高时，陀螺效应成为主要耦合因素。为了解决陀螺效应带来的耦合问题，建立了磁悬浮控制力矩陀螺的α阶逆系统，与原系统串联构成伪线性系统。系统建模误差会使部分残余耦合不能完全消除，因此,根据解耦后的伪线性系统设计滑模控制器来消除参与耦合对系统的影响，控制系统框图如图11所示。仿真结果表明，当系统存在5%的模型非对称性时，该控制方法比PID交叉控制法的超调量小，响应快，解耦控制效果良好。

图11 基于α逆系统的滑模控制系统框图

文献[29]针对磁悬浮控制力矩陀螺微重力、动框架等多元扰动引起的磁悬浮轴承转子系统的强非线性、参数摄动及未建模动态等问题，研究了一种磁悬浮控制力矩陀螺转子系统的指数趋近律积分滑模控制方法。在建立工作点线性化的简化模型基础上，设计了包含转子位移和控制电流作为被控对象的双变量非线性积分滑模面，该滑模面由转子位移误差项、位移误差一阶导数项、位移误差积分项和控制电流误差项构成，通过采用指数趋近律和边界层法饱和函数抑制抖振。试验时设置平衡位置的变化来模拟系统参数摄动情况下系统的响应，结果表明，系统刚度变化时，该滑模控制方法能够使转子小超调快速平衡于新平衡位置。

文献[30]针对磁轴承转子在运行过程中存在的不平衡扰动和陀螺耦合问题，研究了四自由度主动磁轴承系统的交叉反馈解耦滑模控制。考虑系统转子不平衡扰动力和陀螺耦合建立系统模型，设计比例系数项乘以微分系数项，将系统状态方程建立成各状态变量之间无耦合的独立系统，从而实现系统的交叉反馈解耦，并为解耦后的系统设计了滑模控制器，仿真结果表明，该方法的跟踪特性和抗干扰特性较好，能够有效解决不平衡扰动和陀螺耦合问题。

2017年，文献[38]针对五自由度主动磁轴承系统因传感器位置产生的耦合问题，对系统状态变量进行解耦变换，建立输出量解耦的状态方程，并设计了多输入多输出的积分滑模变结构控制器。仿真结果表明，基于传感器位置解耦的多输入多输出积分滑模控制比PID控制器静态误差小，响应时间短，鲁棒性好，无振荡现象。

图12 主、被动磁悬浮转子不平衡振动自适应控制

双万向节磁悬浮控制力矩陀螺扭转运动与转速之间具有耦合，并且同一轴上的扭转运动和平动之间由于位移刚度的不对称性也存在耦合，为此，文献[32]针对不对称位移刚度设计了补偿方法，从而实现平动和扭转运动的分离，并采用积分滑模控制使平动和扭动稳定。为了减少平衡环动作引起的耦合转矩，设计了一种考虑耦合转矩的切换函数，采用极点配置法实现扭转运动的解耦控制，并基于Lyapunov和状态空间法分析了闭环系统的稳定性，该控制系统框图如图13所示。试验结果表明，该控制方法能够减小转子振动，增强系统对误差的鲁棒性，有效提高控制精度。

图13 基于运动分离的磁悬浮转子控制系统框图

从产业结构角度出发，我们可以看到，中国是以制造业为主，劳动力市场上多是体力劳动者，这部分人依靠他们的体力劳动取得收入，但是人体在晚年时期身体机能会大大下降，如果推迟退休年龄会给这些人带来身体上的伤害。

图14 滑模扰动观测器控制系统框图

2018年，文献[39]研究由洛伦兹力式磁轴承驱动转子的磁悬浮灵敏陀螺的精密控制。该系统的控制精度很大程度上由磁轴承磁密分布的均匀性决定，因此将永磁体环的截面改为梯形结构来削弱尖端磁场，并在永磁体内环面贴置了磁性薄片，使气隙中的磁密能够均匀分布，该磁轴承将控制线圈放置在内、外2个环形永磁体中间，利用线圈在磁场中通入电流后产生的洛伦兹力来控制转子的径向扭转。为了使转子能够很好地跟踪给定信号，从而实现高精度和带宽倾斜力矩，采用滑模控制解决系统模型误差带来的问题，并采用交叉反馈控制克服陀螺效应产生的径向2个自由度之间的耦合问题。仿真结果表明，交叉反馈环控制在阶跃扰动和周期阻尼扰动情况下均能很好地跟踪给定信号，并且具有较高的控制精度。

2016年，文献[35]为了消除磁悬浮力矩陀螺的振动，基于滑模观测器提出了一种自动平衡控制方法。首先，建立计及惯性轴偏转的系统动力学方程，并在对悬浮力表达式进行Taylor展开时保留电流刚度和位移刚度随电流、位移变化的特性，考虑气隙磁场变化引起感应电动势变化的电压功率放大器模型，在此基础上建立系统状态方程；然后,根据状态方程设计了滑模观测器来获得较为精确的转子不平衡信息，将转子不平衡与位移传感器检测量相结合求出理论惯性轴，并设计了一种自适应补偿算法得到目标线圈电流补偿位移刚度，从而输出零振动的电磁力，使惯性轴稳定。控制系统结构框图如图15所示，图中:Cr(s)为位移反馈控制器；ACM为自适应补偿模块；SMO为滑模观测器模块。仿真和试验结果表明，该滑模观测器能够对数学模型线性化引起的参数不确定性和扰动表现出良好的鲁棒性，自适应补偿功率放大器的误差和变换，大大减小了振动力和偏转力，从而使转子围绕理论惯性轴旋转。

图15 零振动力转换控制系统框图

文献[36]为了减小磁轴承功率消耗，研究了基于自适应反推滑模控制方法，实现磁悬浮主轴系统的零偏置电流控制。首先，考虑参数不确定性导致的磁轴承悬浮力系数的不确定性和外部干扰力，建立八极径向主动磁轴承的系统非线性数学模型，建模时限定每个时刻同一方向上的2个磁极中只有一个通入电流，实现零偏置电流控制；然后，设计滑模控制器。实际应用中，由于系统总的不确定性上限很难确定，传统的滑模控制器很难选择一个保证系统全局稳定且具有较好控制性能的参数，因此将滑模控制和反推控制相结合，并用一个自适应律实时估算总不确定性的上限，该控制系统框图如图16所示。试验和仿真结果表明，自适应反推滑模控制比普通滑模控制和PID控制具有更好的抗扰动特性，并且零偏置电流控制方法大大降低了系统的功耗。

目前世界各地国家公园的管理模式和体制各有不同，但设立国家公园的目的从早期的保存、保护到现在的集生态保育、科研、游憩、教育、社区发展为一体的综合管理，并逐步开始尊重国家公园内及周边的原住民、当地社区的文化和社会价值，尊重原住民、当地社区的权利，积极引导社区参与国家公园的建设、管理与保护。在我国的《总体方案》中，也提出要“建立社区共管机制”。

图16 零偏置电流磁轴承自适应反推滑模控制系统

文献[37]针对磁轴承多变量非线性导致控制不精确的问题，将反演控制与滑模控制方法相结合，既消除了滑模控制的抖振，又使系统具有较好的鲁棒性。对磁轴承悬浮力方程在平衡点进行Taylor展开得到近似线性化模型，针对线性化的数学模型设计滑模控制器和反演控制器，利用反演控制器将磁轴承系统分解为基于虚拟状态变量的2个子系统，采用滑模控制器来补偿数学模型参数摄动和外部扰动。仿真和试验结果表明，该控制方法具有较快的响应速度，并且动静态性能良好。

2015年，文献[31]针对主、被动磁轴承支承的控制力矩陀螺转子高速旋转时产生的不平衡振动问题，提出了基于滑模观测器和陷波器的不平衡振动自适应控制方法。考虑不平衡振动在径向2个平动自由度上产生的径向力，建立主、被动磁悬浮控制力矩陀螺的动力学模型，分析了主动磁轴承电流刚度、位移刚度随位移和电流变换的关系，将被动磁轴承的径向位移刚度随转子扭转角变化，以及转子的不平衡振动抑制都考虑在内。利用滑模控制方法构造了滑模观测器，其在主动磁轴承径向位移、电流刚度变化以及被动磁轴承位移刚度变化的情况下仍能够对不平衡力进行准确观测。根据补平衡力的观测值进行位移解算，得到转子惯性轴相对于几何轴的位移，再乘以一定的放大系数，与几何轴位移乘以放大系数之和作为陷波器的输入。陷波器的输出与控制器的输出叠加作为系统的总控制信号，由于功放环节在振动控制算法的闭环内，在振动抑制算法迭代过程中能够自适应消除功放环节的影响，其控制系统结构框图如图12所示。试验结果表明，该方法能够减少77%的同频振动，系统的不平衡振动得到了有效抑制。

全新奥迪A8L的强大绝非这千余字的文章所能深入描述，但它的豪华，它的质感，它的科技和它所代表的豪华旗舰面对未来所展现出的领先理念都是令人印象深刻的。奥迪用全新A8L强大的产品力和前瞻的视野给予“突破科技，启迪未来”这句口号奉上了一个完美的印证。

文献[34]研究了一种离散模糊自适应滑模控制系统，用于解决4自由度径向主动磁轴承-转子系统运行中存在的不平衡扰动和非线性干扰问题。首先，建立系统的解耦状态方程并进行离散化;然后，基于离散控制律设计模糊控制器，设计二阶离散非线性跟踪微分器，以系统输出获得位移及其一阶导数的跟踪信号，以滑模面函数及其变化率作为模糊控制律的输入，其输出作为滑模控制律的增益，自适应调节滑模控制律。仿真结果表明，该方法能有效抑制系统中的不平衡扰动和非线性干扰。

文献[40]针对磁悬浮动量飞轮的磁悬浮力矩之间存在耦合的问题，首先，通过分析磁悬浮转矩的动态特性，将动态跟踪误差当作系统未建模扰动和参数摄动；然后，采用自适应反推滑模控制法实现磁悬浮姿态轮的倾斜角精确控制，其中积分滑模面考虑完整的角度误差和跟踪误差。由于切换增益越大，系统越稳定，但会带来系统抖振，使控制精度降低，因此采用模糊算法，以滑动值和倾斜角作为模糊算法输入，以切换增益作为模糊算法输出，自适应调节切换增益，该控制系统结构框图如图17所示。试验结果表明，该控制方法与无自适应的反推滑模控制法和交叉反馈控制相比具有较好的精度和跟踪特性。

图17 模糊自适应反推滑模控制系统框图

2 磁轴承滑模控制应用方式总结

根据上述文献，滑模控制在磁轴承中的应用主要具有以下作用：

1)提高系统的鲁棒性。由于滑模控制方法对系统参数变化的不敏感性，因此磁轴承的模型参数摄动，载荷变化，外部扰动对滑模控制器的控制性能影响较小。

2)观测系统。由于滑模控制方法的鲁棒性强，可通过测量实际系统的输入输出观测系统的内部状态变量，或者构造滑模扰动观测器得到系统扰动，从而对系统扰动进行补偿控制。

十、神矮LS—1苹果其他品种及砧木种子 太平洋嘎拉、五代红星、昌红、烟富（1～6号）、南阳富士、高桩短富；Jm7号、八棱海棠、杜梨、山毛桃、山杏等种子。

3)抑制转子不平衡振动。由于磁轴承转子系统的不平衡振动具有同频特性，因此可将其当作同频的信号扰动，采用滑模控制进行抑制。

4)抑制磁悬浮转子的陀螺效应。由于磁轴承转子常工作于高速场合，陀螺效应对磁轴承控制系统的影响较大，且随转子转速的变化而变化，而滑模控制法对参数变化具有不敏感性，因此能够抑制不同转速下陀螺效应的影响。

3 磁轴承滑模控制的发展趋势

从国内、外磁轴承滑模控制的研究现状来看，目前滑模控制在磁轴承中的研究趋向以下方面：

一般检修举措往往会耗费大量的人力、物力、财力,且故障排查不及时,不能消除潜在的安全隐患,往往会造成重大安全事故。而安全有效的带电检测不仅可以大大降低设备损坏的可能性,延长开关柜的使用寿命,而且还能使整个供电系统拥有长期稳定的保障。

1)滑模控制的抖振。抖振是滑模控制的缺点之一，是所有滑模控制的共性问题，虽然目前减小抖振的方法较多，但缺乏能够完全消除系统抖振的方法。

对于像戴表元这一类由宋入元的文化人出仕现象，申万里认为：“元初江南儒士社会角色的转变,在当时仍然具有重要的历史意义,它不仅为元代儒学的恢复和发展创造了条件,保证了汉文化在元代的发展和传承,也有利于江南社会的稳定和经济文化的发展”[17]，信哉斯言！戴表元任信州路儒学教授期间，进行了一系列文化活动：教授生徒、刻印书籍、交往学人等等，为传播文化尽心尽力。任期内的《北史》刊刻，更是一件大事，当另撰文论述。

2)滑模控制的自适应性。磁轴承是一个非线性和系统参数变化性都很强的系统，虽然滑模控制具有很好的鲁棒性，但在系统不确定性变化上界发生变化时仍会影响控制系统性能。另外，若作为观测器使用，其增益还需自适应系统参数的变化。

3)滑模控制的精确性。磁轴承是一个需要精确控制的系统，尤其是在电主轴、姿态飞轮等领域，因此需要尽可能提升其控制精度。

4)滑模控制与其他控制方法的结合。滑模控制有其独特的鲁棒性强的特点，若与其他控制方法结合，取长补短，则能进一步提升控制系统的性能。

5)高转速、超高转速下滑模控制方法的应用。磁轴承的主要特点是能够在高转速下无摩擦运行，但由于高转速会引起转子不平衡振动，穿越临界转速，柔性转子等问题，需要更深入的研究才能取得更好的控制效果。

6)不同磁轴承结构和磁轴承整体系统的控制。目前磁轴承滑模控制研究大多是针对单个主动磁轴承，不同磁轴承结构具有不同的悬浮力特性，尤其是混合磁轴承功耗极低，但其控制比主动磁轴承复杂、困难，因此混合磁轴承及其构成的磁悬浮系统的滑模控制还有待进一步研究。