混凝土箱梁相似模型结构噪声对比分析∗

雷晓燕 欧开宽 罗 锟 汪振国 曾少辉

(1华东交通大学 铁路环境振动与噪声教育部工程研究中心 南昌 330013)

(2南昌华路建设咨询监理有限公司 南昌 330013)

0 引言

列车在桥上运行会导致桥梁各个结构的振动，进而形成桥梁的结构噪声[1]。桥梁结构各板件产生的结构噪声频率低、衰减慢，对桥梁周围的居住环境造成一定的影响[2−3]。许多学者对铁路桥梁频域内结构噪声进行了大量的研究[4−9]。张迅等[10]根据瞬态声辐射理论，对铁路32 m简支箱梁结构噪声的时变特性进行了分析。尹镪等[11]利用有限元及边界元法，对铁路32 m简支箱梁时域内结构噪声进行研究，研究结果为实际应用提供了一定的参考。程海根等[12]对变截面箱梁箱内时域内噪声分布特性进行研究，研究结果为降低箱内噪声提供了依据。

目前，国内外学者对于铁路桥梁结构振动与噪声的研究中，采用混凝土箱梁相似模型研究箱梁结构振动与噪声问题相对较少，对于研究混凝土箱梁相似模型结构噪声之间的关系，亦相对较少，本文通过研究箱梁相似模型结构噪声的关系，可为箱梁缩尺模型结构噪声研究反演至箱梁原型结构噪声研究提供一定的依据，文中所采用的方法和得到的结果对桥梁结构振动与声辐射实验研究具有参考作用。

1 瞬态声辐射理论及边界元算法

瞬态声场中，三维波动方程可以表示为[10]

式(1)中：p为声压；∇2为三维拉普拉斯算子；x为空间中任意观测点的坐标；c为声速；t为时间。

式(1)可通过单位声源函数式(2)、式(3)求得：

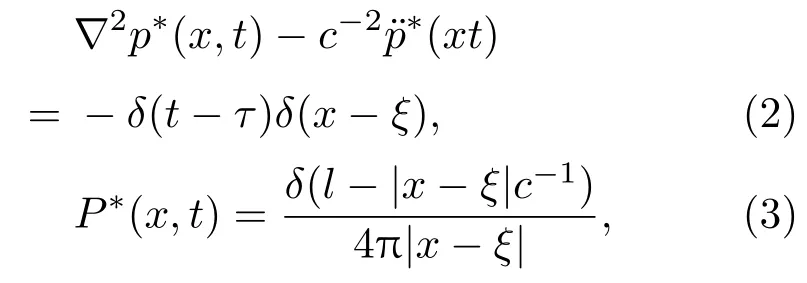
其中：P∗(x,t)为基本解；ξ为声源坐标；δ为克罗内克函数；τ为δ(t−τ)中脉冲激励的时刻。

箱梁板件的振动为式(1)的边界条件，即

式(4)中：ρ0为空气密度；an为箱梁表面的法向振动加速度；n表示箱梁表面的外法线方向。

式(1)的初始条件可以表示为

即无车通过时，箱梁不发生振动，也不辐射噪声。

联立式(1)、式(4)和式(5)，可得到声波传播方程：

式(6)中：S为振动体箱梁表面；C(ξ)=α(ξ)/4π为振动边界的空间角系数，对于平滑边界α(ξ)=2π。

对于比较复杂的振动体的声辐射，式(6)需要在时间域和空间域进行离散，可以采用边界元法进行数值求解。本文基于瞬态边界元法，利用Virtual.Lab对箱梁结构的瞬态噪声进行仿真计算。

2 箱梁结构分析模型

2.1 箱梁缩尺模型

京沪高速铁路简支箱梁几何尺寸为长×宽×高 =32 m×12 m×3.05 m。考虑施工便利和模型试验精度的要求，箱梁模型与原型的几何相似比设定为1:10，混凝土箱梁的几何尺寸如图1所示。根据模型相似理论分析可知，在弹性阶段的动力相似关系仅与材料的弹性模量、密度、缩尺比例有关且相互独立，可以自由选择[8]。因此，模型浇筑材料选用自密实混凝土，钢筋利用直径为5 mm的钢丝代替。为了保证箱梁成型质量，施工分四步完成：(1)支外模，绑腹板和底板钢筋；(2)支内膜，浇筑腹板和底板混凝土；(3)绑顶板混凝土，浇筑；(4)成型。施工过程如图2所示。在同等条件下养护28天后，对混凝土试块进行弹性模量和密度等参数的现场测试，结果为E=30e9Pa，ρ=2203.7 kg/m3。模型箱梁和桥墩之间通过弹性支座连接，支座刚度为2.8e8N/m。

图1 箱梁几何尺寸(单位：mm)Fig.1 Geometry of box girder

图2 箱梁模型的制作Fig.2 Production of box girder scale model

根据实测的箱梁模型系统参数与京沪高铁原型箱梁参数，利用相似第一定理(相似正定理)、相似第二定理(Π定理)、相似第三定理，以及弹性力学方法推导的模型试验的实际相似常数，见表1。

表1 箱梁模型与原型间的参数相似比Table 1 Similarity ratio between box girder model and prototype

2.2 箱梁模态试验

利用约束模态试验的方法验证箱梁缩尺模型与箱梁原型具有系统相似关系。测试时，使用激振器在箱梁角点进行激励，激励信号选用触发随机信号，如图3所示。图4为测点布置图，测点沿箱梁缩尺模型纵向每隔0.4 m选择一个测试截面，共9个截面，每个截面分别在顶板和底板分别选择5个和3个测点，合计72个测点。模态测试过程中，72个测点分8批次进行，每次选纵向9个测点，测试时仅传感器移动，激振器位置保持不变。

模态测试结果与箱梁缩尺模型和原型的计算结果对比如表2所示。前3阶次的模态振型对比如图5所示，其中左侧为缩尺模型有限元仿真模态振型，右侧为实测模态振型。对比表2及图4可知：(1)实测与理论的模态频率误差在1%左右，仅第2阶为5.75%；(2)箱梁模型与箱梁原型之间符合相似关系，箱梁模型的振动噪声测试结果能真实反映原型振动噪声水平；(3)本文建立的缩尺箱梁有限元模型是正确的。

图3 箱梁约束模态试验Fig.3 Constrained modal test of box girder

图4 箱梁72测点几何模型Fig.4 72 point geometries of box girder

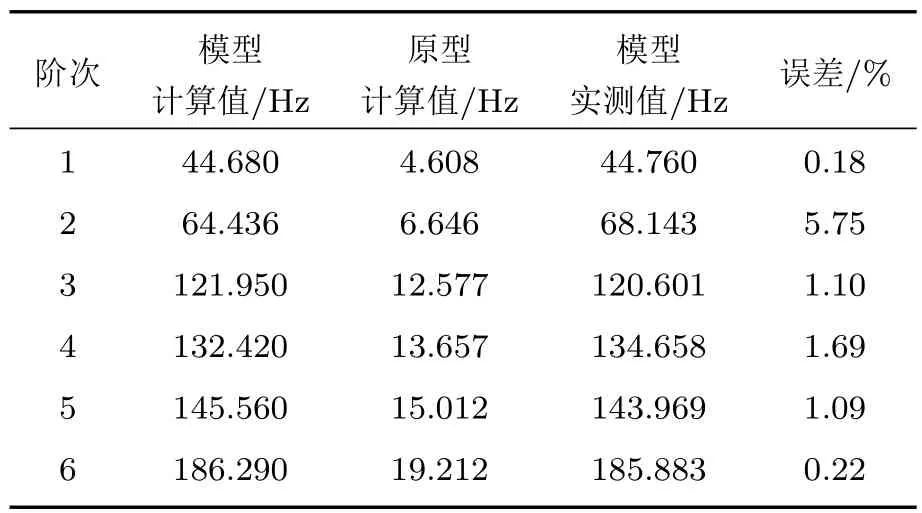
表2 箱梁约束模态实测值与计算值对比Table 2 Comparison of measured and calculated values of box beam constrained modes

图5 箱梁实测模态与有限元计算模态对比Fig.5 Comparison of measured modal and finite element computational modes of box girder

2.3 箱梁声学试验

将缩尺箱梁置于半消声室内，在箱梁跨中断面布置声学传感器进行声压级实测，用以验证箱梁结构噪声的计算模型。采用的仪器有激振器、德国HEAD振动噪声采集分析系统和GRAS声学传感器。在跨中断面布置6个GRAS声学传感器，包括顶板上方0.03 m和0.6 m位置共2个，底板下方0.03 m和0.6 m共2个，翼板下方0.03 m和0.5 m位置共2个，布置如图6所示。激励方式为采用谐荷载在箱梁角点进行激励，荷载幅值为20 N，频率为1∼200 Hz，方向向上。测试前，对激振器做一定的隔声处理，尽最大可能避免影响测试结果。测试共分3组进行，每组测试时间60 s。实测如图7所示。

图6 场点及激励点位置(单位：m)Fig.6 Field point and excitation point position

同时，利用有限元和边界元相结合的方法计算箱梁跨中断面不同位置的声压值。计算频率同测试频率，为1∼200 Hz。同时考虑到地面反射作用，用障板模拟地面。为便于验证，在数值计算时，提取同测试场点相同位置的计算结果进行对比，结果如表3所示。

图7 声压级实测图Fig.7 Sound pressure level measurement

表3 实测声压级与仿真值对比Table 3 Comparison of measured sound pressure level and simulation value(单位：dB)

通过对6个场点的实测结果和数值计算结果对比分析，可知实测结果和预测结果较为相近，多数场点仅相差1 dB，只有场点6一点相差3 dB。因此可以认为本文所建立的箱梁声学仿真计算模型与方法是正确的，用该模型来计算箱梁的结构噪声结果是可靠的。

3 箱梁瞬态声辐射计算模型

由上述箱梁约束模态试验与声学试验可知，建立的缩尺箱梁有限元模型和声学计算模型是正确的。同样，利用ANSYS建立箱梁原型的有限元模型，箱梁原型与缩尺模型网格划分时单元几何尺寸比为1:10，单元与节点数目保持相同。分别对箱梁原型与缩尺模型进行瞬态分析，经验证瞬态分析计算的箱梁原型的振动响应与理论推导的数值结果基本吻合。

为方便研究箱梁原型与缩尺模型结构噪声之间的关系，对模型作了一定的简化，有限元模型中只考虑梁体结构部分，不考虑轨道板、混凝土底座等结构，同时对两种模型有限元瞬态分析中采用简单激励来模拟加载，进行结构声辐射的计算。首先，在缩尺箱梁有限元模型上施加轮对力，进行瞬态分析；同时按照上述相似比尺在原型中施加相应的一对轮对力进行瞬态分析。其中原型轮对力横向间距为作用在标准轨距上的距离，而缩尺模型上轮对力横向间距为原型距离的1/10。经验证原型桥与模型桥瞬态分析的振动响应满足上文中的相似比尺。然后将两种模型的有限元振动响应导入Virtual.Lab中作为边界条件，计算出两种模型的瞬态结构噪声及进行对比。箱梁轮对力加载方式如图8所示。箱梁原型与缩尺模型主要的计算参数如表4所示。

为对比两种桥瞬态声场特性，在箱梁原型的跨中横断面处建立一个15 m×15 m的平面场点，然后取箱梁一半平面场点进行研究，在缩尺模型的跨中横断面建立一个同样的平面场点，该平面场点尺寸为原型平面场点的1/10，即1.5 m×1.5 m。同时在箱梁跨中横断面建立一系列的场点，其中Y1∼Y4、S1∼S4分别为箱梁原型与缩尺模型跨中横断面场点。Y1∼Y2位置在梁底板中心线下，距底板的距离依次为2 m、6 m；Y3∼Y4位置距底板的距离为6 m，距梁底板中心线的距离分别为7 m、14 m；S1∼S2位置在梁底板中心线下，距底板的距离依次为0.2 m、0.6 m；S3∼S4位置距底板的距离为0.6 m，距梁底板中心线的距离分别为0.7 m、1.4 m。箱梁场点网格如图9所示。

图8 箱梁有限元模型及轮对力加载方式Fig.8 Finite element model of box beam and wheel load on the way

图9 箱梁场点网格Fig.9 Field point grid of box beam

表4 两种模型的主要计算参数Table 4 Main calculation parameters of the two models

4 箱梁相似模型瞬态声辐射特性对比

采用瞬态边界元法进行箱梁结构瞬态声辐射特性分析，能够很好地体现桥梁结构声场随时间的变化规律，同时可以较为快速地提取各时间节点桥梁振动云图和声场云图。为了较为清楚地对比原型桥与模型桥结构声辐射特性，分别选取激励力刚开始作用箱梁、激励到达四分之一跨、激励到达跨中及激励离开桥梁时的四个时间段作为时刻A、时刻B、时刻C及时刻D，然后对不同时刻下两种模型对应声场的声压级云图及场点声压特性两个指标展开对比分析。

4.1 声压级对比

分别对时刻A、时刻B、时刻C及时刻D四个时刻的箱梁结构的二维声压级云图进行对比，如图10所示，左侧为箱梁原型的二维声压级云图，右侧为箱梁缩尺模型的二维声压级云图。

由图10可知：(1)箱梁的声学响应符合声学规律，板附近声压级最大并逐渐向四周衰减；(2)不同时刻的箱梁原型与缩尺模型声压级云图相似，尤其是在箱梁顶板、翼缘板、腹板和底板附近区域，二者云图几乎相同，声压级相差不大。(3)时刻A、时刻B、时刻C及时刻D四个时刻，由于边界效应等原因，导致荷载刚踏入或驶离箱梁时声压级相差偏大。在时刻A，箱梁原型顶板、翼缘板、腹板和底板周围的声压级约为−8.59 dB，而箱梁缩尺模型为−11.6 dB，二者相差约为3 dB；时刻D，箱梁原型的顶板、翼缘板、腹板和底板周围声压级约为76.9 dB，缩尺为80.7 dB，二者相差约为3.8 dB；而在1/4断面时刻B，箱梁原型顶板、翼缘板、腹板和底板周围的声压级约为78.2 dB，而缩尺模型为76.3 dB，二者相差减少约为1.9 dB；当荷载在跨中时刻C时，箱梁原型顶板、翼缘板、腹板和底板周围的声压级约为82.6 dB，而缩尺模型为82.7 dB，二者几乎相等，相差仅为0.1 dB。因此，从声压级云图对比可知，箱梁原型与缩尺模型在声压级方面存在一定的相似关系。

图10 二维声压级云图对比(单位：dB)Fig.10 Comparison of 2-dimensional sound pressure level cloud

4.2 场点声压对比

分别提取箱梁原型与缩尺模型上述四个场点的声压响应函数进行对比。由表2可知，二者在时间历程上并不是一一对应的，而是有一个相似比尺。为便于在时域内进行比较，现将箱梁缩尺模型场点的时间历程乘上时间比尺，这样二者场点声压值在时域内相对应。经这种特殊处理后的“缩尺模型场点声压”与箱梁原型场点声压对比结果如图11所示。

由图11可知，箱梁原型与缩尺模型在对应场点声压幅值及变化趋势很接近。随着距离的增加，各场点的最大声压开始衰减。而且随着距离的增加，各场点最开始出现声压的时刻有所延迟，这是因为各场点有一定距离，声压传播需要一定的时间。因此，箱梁原型与缩尺模型不同场点时域内声压存在一定的相似关系。

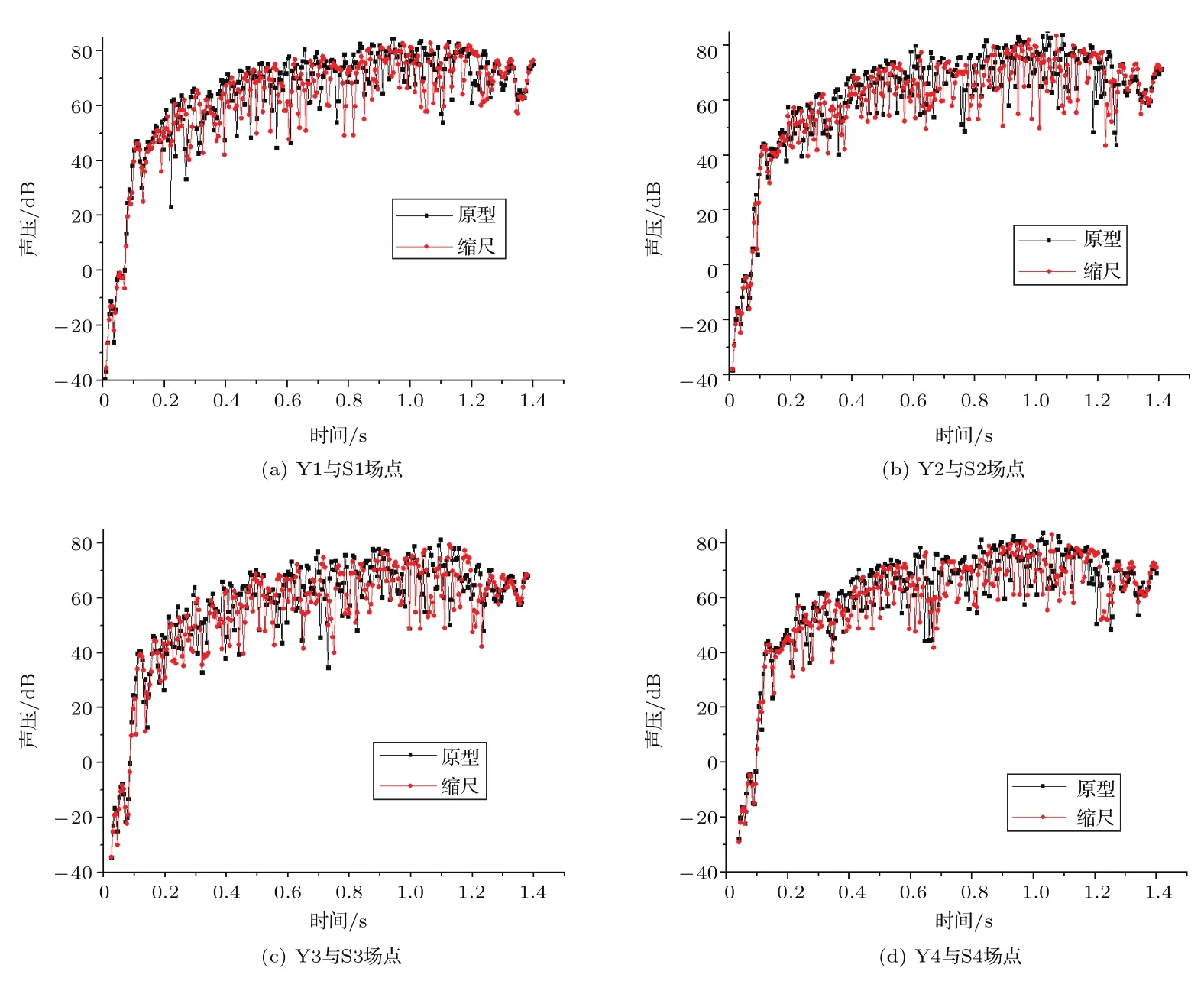
图11 场点声压对比Fig.11 Field pressure characteristics of contrast

5 结论

本文基于瞬态边界元法，研究了32 m混凝土简支箱梁和与其对应的1:10缩尺模型结构噪声在时域内的相似关系。通过对比二者声场声压级云图及场点声压等指标，主要结论如下：

(1)基于几何相似制作的箱梁缩尺模型与箱梁原型的材料参数满足一定关系，模型试验的方法能够验证箱梁模型与箱梁原型之间符合相似关系，箱梁模型的振动噪声测试结果能真实反映原型振动噪声水平。

(2)箱梁缩尺模型与箱梁原型结构噪声在时域内的声压级云图相似，二者时域内声压级之间存在一定相似关系；二者结构噪声在时域内对应场点的声压存在一定相似关系。

(3)本文可为箱梁缩尺模型结构噪声反演至箱梁原型结构噪声的研究提供依据，文中采用的方法和得到的结果对桥梁结构振动与声辐射实验研究具有参考作用。