一种改进的DNN-HMM的语音识别方法∗

李云红 梁思程 贾凯莉 张秋铭 宋 鹏 何 琛王刚毅 李禹萱

(1 西安工程大学电子信息学院 西安 710048)

(2 国网西安供电公司 西安 710032)

0 引言

声学模型作为语音识别系统的主要模型之一，利用一系列声学特征完成建模训练，能够明确各声学基元相关发音模式。目前广泛应用的声学建模研究主要围绕高斯混合模型隐马尔可夫模型(Gaussian mixture model-hidden Markov model,GMMHMM)[1]展开。胡政权等[2]提出了梅尔频率倒谱系数(Mel-frequency cepstral coefficients,MFCC)参数提取的改进方法。赵涛涛等[3]提出了经验模态分解和加权Mel倒谱的语音共振峰提取算法。但是，随着深度学习在词识别率方面取得跨越性突破后，应用它建立声学模型成为了研究人员关注的焦点[4−8]。

2000年，深度学习领域的专家Hinton等[9]提出了限制玻尔兹曼机(Restricted Boltzmann machine,RBM)，这种模型结构是可见层节点与隐藏层节点全部连接，相同层节点之间互相独立。2006年，Hinton等提出了基于层叠的RBM算法，即深度置信网络(Deep belief networks,DBN)，表明了深层神经网络模型在特征提取以及模型表达方面具有优异的表现。Mohamed等[10]首次使用DBN来取代传统的GMM来为HMM状态输出特征分布建模，并成功搭建DBN-HMM声学模型应用于一个单音素识别系统，通过实验表明在词错误率方面下降到了20.3%。最近几年，国内外专家学者在声学特征方面进行深入研究，使得深度学习理论在语音识别领域再次有了进一步的发展。张劲松等[11]比较了几种不同特征对识别率的影响，使用Mel滤波器组系数(Mel-scale filter bank,Fbank)作为声学特征，具有更好的识别率。Kovacs等[12]更是在Fbank特征基础上利用自回归的方法来调整模型的鲁棒性，取得了较好的识别结果。

理论方面，经过多年研究发展，深度学习理论与语音识别技术的结合[13−14]已然达到较为成熟的阶段；应用方面，从最初的人工神经网络(Artif icial neural network,ANN)到现在的深层神经网络(Deep neural network,DNN)，可以说神经网络已经达到实际应用阶段[15]。Salakhutdinov等[16]提出的深度玻尔兹曼机(Deep Boltzmann machine,DBM)以RBM为基础，模型中单元各层均为无向连接，使模型处理不确定样本的健壮性更强。基于此，论文结合DBM，在Kaldi平台上建立改进的DNN-HMM语音识别模型[17]，经语音识别库TIMIT的测试实验，取得了较好的语音识别结果。

1 改进的DNN-HMM声学模型

图1 模型结构Fig.1 Model structure

DNN-HMM声学模型是由DBN模型组成的深度神经网络，DBN模型隐藏层采用RBM组成的有向图模型。而改进的DNN-HMM声学模型由DBM模型和DBN模型混合而成。模型结构对比如图1所示。DBM模型是由两层RBM组成的无向图模型，每层节点的采样值均由两层连接的节点共同计算。但是DBM模型训练时间长度与它的层数和每层的节点数有关。DBN模型是由四层RBM组成的有向图模型，在预训练过程中，上层是输出，下层是输入。所有层训练完毕后，由最上层开始向下进行有监督微调。

如图1所示，DNN-HMM模型和改进的DNNHMM模型都有1个输入层，4个隐藏层，1个输出层。h1、h2、h3、h4分别对应4个隐藏层，W1、W2、W3、W4、W5分别对应层间的连接权重。模型相同层节点不连接，不同层节点之间全部连接。DNN-HMM模型输入层、h1、h2、h3、h4之间是有向图全连接的DBN模型。改进的DNN-HMM模型的输入层、h1、h2之间是无向图全连接的DBM模型，h2、h3、h4之间是有向图全连接的DBN模型。固定长度的向量作为模型输入，改进的DNN-HMM模型先由h1、h2训练，h2作为DBM模型的输出层，同时也是h3、h4的输入，输出是当前输入信息的特征表示。

RBM是基于能量的模型，可以捕获变量的相关性。其定义为

公式(1)表示每一个可视节点与隐藏节点之间构成的能量函数。其中，m是可视节点的个数，n是隐藏节点的个数，b、c是可视层和隐藏层的偏置。由于RBM目标函数要累加所有可视层和隐藏层节点取值的能量，其计算也面临指数级的复杂度。因此，将计算能量累加转换为求解概率的问题，即得到的v,h的联合概率为

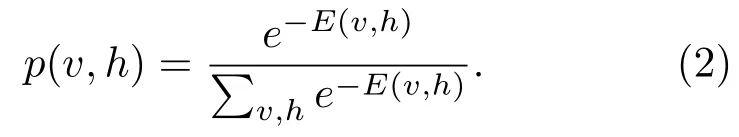
通过公式(2)简化能量函数的求解，使得求解的能量值最小。由统计学的一个理论，能量低发生的概率大，因此引入自由能量函数最大化联合概率，公式如下：

其中，Z是归一化因子，故联合概率可以表示为

公式(5)中等号左边是似然函数p(v)，右边第一项是整个网络自由能量总和的负值。

整个深度神经网络模型应用误差反向传播算法，让目标函数获得最优值，从而达到训练目的。针对深度神经网络进行训练时，目标函数通常替换为交叉熵，在实际优化阶段，使用随机梯度下降法来处理。换言之，对于多状态分类问题中目标函数往往使用取负值的对数概率，如公式(6)所示：

其中，sut是t时刻的状态，FCE为状态标签与预测状态分布y(s)之间的交叉熵。目标函数与输入aut(s)间的梯度可以记为

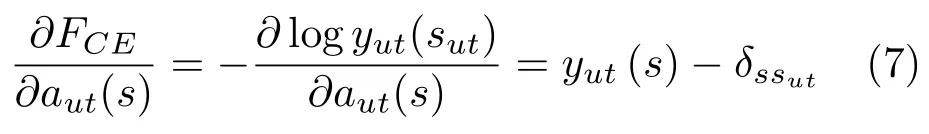
公式(7)中δssut是克罗内克函数，满足：

由公式(8)，网络参数的调整方法使用反向传播算法。

改进的DNN-HMM模型与DNN-HMM模型不同的是底层使用了DBM模型对输入的语音信号进行了处理。DBM模型中每一个隐藏节点的状态都由它直接连接的上下层节点共同计算决定，因此相比DNN-HMM模型可以对输入的语音信号进行更好的降维，捕捉不同语音的特征。同时，高层采用DBN模型结构避免了DBN模型开始训练时容易过拟合的现象，保持了良好的性能。

2 Fbank特征

在语音识别领域当中，使用对角协方差矩阵的GMM，将MFCC作为声学特征一直是研究的常用手法。MFCC声学特征的计算过程如图2所示。

图2 MFCC计算流程图Fig.2 MFCC flow chart

如图2所示，经预处理和快速傅里叶变换(Fast Fourier transformation,FFT)得到语音信号各帧数据的频谱参数，通过一组N个三角带滤波器构成的Mel频率滤波器作卷积运算，然后对输出的结果作对数运算，依次得到对数能量S(m)m=1,2,3,···,N，最后经离散余弦变换(Discrete cosine transform,DCT)，得到MFCC参数，如公式(9)所示：

其中，n代表MFCC声学特征的个数，Ci(n)是第i帧的第n个MFCC系数，作为log对数能量模块的输出，M是Mel滤波器的个数。

Fbank声学特征省略了MFCC声学特征提取过程的DCT模块，将log对数能量模块的输出直接作为输入语音的声学特征。在三角滤波器组模块，使用N个三角带滤波器就可以得到N维相关性较高的Fbank特征。而经过DCT计算提取的MFCC特征，将能量集中在低频部分，具有更好的判别度。

因此，使用GMM进行语音识别时，由于GMM忽略不同特征维度的相关性，MFCC特征更加适合。而基于深度神经网络的语音识别中，深度神经网络可以更好地利用Fbank特征相关性较高的特点，降低语音识别的词错误率。另外，Fbank声学特征相比MFCC声学特征，减小了声学特征提取时的计算量，容易进行带宽调节，得到最佳带宽的识别结果，从而进一步提高语音识别的正确率。

3 实验过程与结果分析

3.1 实验过程

3.1.1 GMM-HMM声学模型的建立

(1)特征提取

实现帧长25 ms、帧移10 ms、特征维度39维(12维输出、1维对数能量及两者一阶、二阶差分)的MFCC特征的提取，然后进行倒谱均值方差归一化的处理。

(2)训练GMM-HMM模型

在模型训练过程中考虑将上下文相关的三音素融入声学模型，并以此作为声学基元进行模型训练，最后将训练后的模型输出特征进行解码。

在Kaldi开发平台中，三音素模型采用A_B_C结构形式，其中B为当前状态，A和C为上下文。训练过程如表1所示。首先进行单音素模型训练，并按照设置的次数对数据对齐，然后以单音素模型为输入训练上下文相关的三音素模型并实现数据对齐，接下来对特征使用线性区分分析(Linear discriminant analysis,LDA)和最大似然线性回归(Maximum likelihood linear transform,MLLT)进行变换并训练加入LDA和MLLT的三音素模型，最后进行说话人自适应训练(Speaker adaptive training,SAT)得到LDA+MLLT+SAT的三音素模型，整个过程逐步实现了特征参数的优化。

表1 基础模型训练过程Table 1 Basic model training process

最后对识别结果进行强制性对齐，获得聚类后每个三音素的状态号来作为深度神经网络训练调谐时候的标签信息，并以此作为训练DNN模型和改进的DNN模型的基础模型。

3.1.2 深度神经网络声学模型的建立

(1)监督信息的生成

因为RBM模型训练不适用不同长度的语音音素，论文通过强制对齐GMM-HMM基线系统识别结果，得到各聚类三音素状态，即模型DNN和改进模型DNN网络调参过程中所需标签信息。

(2)特征提取过程

在进行深度神经网络模型训练时，使用基于MFCC与Fbank两种不同的声学特征完成训练与解码，同时变更Fbank特征下滤波器组数量，观察不同滤波器组数量的Fbank特征对DNN和改进模型DNN网络识别结果的影响。

(3)网络参数设定

整个深度神经网络模型包含1个输入层、4个隐藏层和1个输出层，网络输入选择超长帧(连续11帧组成)，隐藏层共有1024个节点，输出层共有1366个节点，各节点关联各种音素标签，输出层用Softmax网络作分类。

另外，由于深度神经网络模型参数调谐过程中需要根据开发集和测试集识别率的对比控制迭代次数。故在训练集中选取3000条语句作为开发集，选择1000条语句构成测试集。

(4)网络训练

首先初始化参数，设置RBM模型迭代20次。设置最小交叉熵为目标函数，借此调整参数。通过开发集与测试集测试得到识别准确率与迭代次数关系如图3所示。

图3 预测准确率与迭代次数变化Fig.3 Prediction accuracy and number of iterations

(5)深度神经网络声学模型

结合深度神经网络输出层节点的输出值计算状态输出的后验证概率，调用Kaldi中的nnetforward工具进行解码识别。

3.2 实验结果

根据上述步骤在Kaldi语音识别系统开发平台上训练单音素模型，并在此模型上优化训练三音素模型作为深度神经网络训练的基础模型。以训练好的三音素基础模型对分别使用MFCC特征和Fbank特征的模型进行训练解码。

整个实验中分别使用了滤波器组数目为8、19、30、41、52、70、81的Fbank特征对DNN-HMM模型和改进的DNN-HMM进行建模，Fbank特征滤波器组数初始值设为8，实验中首先对8组滤波器的Fbank特征进行训练解码，然后修改滤波器组数目进一步实验分析，比较滤波器组数目对实验结果的影响。

一个音素的发音时间一般在9帧左右，拼接特征的选择在9帧以上。实验中，拼接特征选择11帧，左右各5帧。根据Fbank特征滤波器组数目的不同，输入层节点个数分别设置为88、209、330、451、572、770、891。经训练误差的比较后，4个隐藏层节点个数选择1024。输出层1366个节点，关联各种音素标签。

MFCC特征下GMM-HMM、DNN-HMM和改进的DNN-HMM声学模型的句错误率与词错误率如表2所示。改进的DNN-HMM声学模型在不同Fbank特征下的句错误率和词错误率如表3所示，与DNN-HMM的识别率比较如图4所示。

表2 MFCC特征下声学模型的识别率Table 2 Recognition rate of acoustic model under MFCC characteristics

表3 改进的DNN-HMM在不同Fbank特征下的识别率Table 3 Recognition rate of improved DNN-HMM under different Fbank features

图4 改进的DNN-HMM与DNN-HMM模型错误率比较Fig.4 Comparison of error rates between improved DNN-HMM and DNN-HMM models

3.3 实验分析

(1)根据表2的结果可以确定，在MFCC声学特征下，与传统GMM-HMM方法、DNN-HMM方法相比较，改进的DNN-HMM声学建模方法在句错误率与词错误率方面均有下降，分别为22.37%和4.15%。这表明后者在声学建模方面相比DNN模型、GMM模型对于复杂的语音数据有着更强的建模能力。

(2)从表3可以看出，滤波器组数量不断增多时，改进的DNN-HMM模型得到的句错误率与词错误率呈现先降后增的趋势。说明适当的增加滤波器组数量可以使识别结果更好，但是当增加到一定数量时结果反而会下降。论文实验中，滤波器组数量为30时，句错误率与词错误率达到最小值，分别为21.06%和3.12%。

(3)从图4可以看出，改进的DNN-HMM声学模型比DNN-HMM声学模型在不同滤波器组数量时句错误率与词错误率均有所下降，其中在滤波器组数量为默认值时，句错误率下降了0.48%，词错误率下降了0.82%。说明了在相同条件下，改进的DNN-HMM模型相比DNN-HMM模型有更强的建模能力。

4 结论

论文建立了改进的DNN-HMM声学模型，使用TIMIT语音数据集，通过语音识别评价指标句错误率和词错误率分析了不同Fbank特征滤波组对改进的DNN-HMM声学模型的影响，并与DNNHMM在相同实验条件下进行了比较，证明了改进的DNN-HMM声学模型和Fbank参数拥有更强建模能力。论文在改进DNN-HMM模型实验过程中，发现模型前两层的DBM无向图模型可以有效去除噪音，而这也为论文后续的研究指明了一个方向。