高寒区草地-家畜优化配置研究——以青海省玛沁县1牧户为例

孙金金， 焦 婷， 李亚娟， 王 芳， 汪鹏斌， 鱼小军

(甘肃农业大学草业学院， 草业生态系统教育部重点实验室， 中-美草地畜牧业可持续发展研究中心，甘肃省草业工程实验室， 甘肃 兰州 730070)

草地畜牧业在我国占有重要地位，是草原地区的支柱型产业。近年来，很多地区的草原实际载畜量已经远远高于理论载畜能力，这在很大程度上造成草原的破坏或退化。目前，我国草原地区存在夏秋季节饲草丰裕、冬春季节严重匮乏或夏秋季节饲草匮乏而冬春季节丰裕的现象。由于草畜季节不平衡造成的草地不合理利用是草地退化的主要原因[1]。如不考虑季节变化,单纯以饲草总产量为基础来确定载畜量,则不能有效解决我国草原地区普遍存在的季节性草地超载过渡放牧问题[2]。

牧草返青期是草地系统生态最脆弱的时期。在牧草返青期间，刚刚萌发返青的幼苗被采食后光合面积迅速减少，严重影响其后期的生长和发育，且刚刚返青的牧草不能满足放牧家畜的需求，造成放牧家畜的“春乏”现象[3]。有研究表明，通过建设人工草地补饲可增加优质饲草料供给，使天然草地通过禁牧或休牧降低放牧强度；或通过草畜的合理配置，减少牲畜对天然草地的过度采食和践踏，依靠大自然的自我修复能力，可实现草地增产和生态保护[4-5]。

近年来，国内外专家和学者在研究“草畜平衡”问题上有大量报道，Masae[6]研究表明条带式分配的放牧方式是一种节约高产的适用于周期较短的家畜育肥的方式。Hofstede[7]研究得出结论放牧驯养家畜会使草地初级生产力降低。斯日古楞[8]通过研究认为应以改变家庭牧场的生产管理模式，通过对各种生产要素的优化配置，最终实现草畜平衡，提高畜牧业经济效益。闫志坚[9]通过对绵羊舍饲育肥的研究发现舍饲可以提高家畜的出栏率，减轻草地放牧承载压力，减少对草场的破坏，实现草畜平衡。韩国栋[10]提出以有效保护草地生态基本功能和高效利用草地生产资源为核心的草地优化研究理论。闫宏[11]研究表明人工饲养条件下母畜及羔羊的营养状况得到了改善。王启基[12]研究得出在生产结构被优化后，家庭牧场可以通过建设暖棚、人工草场等方式，改善农牧民的家畜饲养情况和生活，并提高生态效益。大量研究表明优化草地-家畜结构可有效改善草地利用状况，提高经济、生态效益。而现有研究中结合气候约束条件，将“草地-家畜-生态效益-经济效益”统一考虑的研究甚少。草地载畜量常使用数量载畜量与营养载畜量中的可消化粗蛋白(digestible crude protein，DCP)和总可消化养分(total digestible nutrients，TDN)载畜量相结合的方法进行评价[13-15]。但是TDN载畜量反映草地能量载畜量尚不精确，而体外产气估测牧草代谢能(metabolic energy，ME)技术的成熟[16-17]，使ME载畜量的计算成为可能。因此，为了协调家庭牧场草地生产的生态和经济功能，以青海省玛沁县一牧户为例，根据家庭牧场的不同草地类型，对其草地进行返青期休牧，对家畜-草地系统进行优化、合理配置，进一步增加对草畜生态系统物质的有效输入，减轻天然草原的承载量，充分利用人工草地高生产力的优势，让天然牧草不仅能全面发挥草原生态的积极作用，还能为推动畜牧业的发展提供必要的支持；进而有效缓解或彻底解决当地放牧家畜缺草的局面，促进草地生态系统的可持续利用和良性循环，使畜牧业生产经营由传统经验性决策，进入科学决策，做到生态、经济、社会效益俱佳。

1 材料与方法

1.1 研究区自然概况

研究点位于青海省玛沁县，地理位置为98°48′～100°55′ E，33°43′～35°16′ N。该地区属高原寒冷气候，主要植被类型有高山草甸、高山灌丛和沼泽化草甸。土壤为高山草甸土、高山灌丛草甸土和沼泽土。地势平坦，海拔3 760 m。年均温-3.9℃，≥5℃积温850.3℃，最冷月1月的平均气温为-12.6℃，最热月7月的平均气温为9.7℃。牧草生长季为156 d，无绝对无霜期。年均降水513.2 mm，年蒸发量2 471.6 mm[18]。该地区普遍存在家畜超载过牧，牧户草地-家畜系统主要存在夏秋季节饲草丰裕、而冬春季节严重匮乏，或夏秋季节饲草匮乏而冬春季节丰裕两种现象。本研究以夏季牧场饲草严重匮乏、秋季牧场可满足家畜数量和营养采食，冬春牧场饲草丰裕但营养不足，存在夏季牧场家畜超载、冬春季牧场营养超载的牧户(表1)为例，进行草地家畜优化配置。牧户草地基本情况见表2。

表1 牧户草地-家畜现状Table 1 The status of herdsmen grassland and livestock

表2 牧户草地-家畜基本情况Table 2 Herdsmen basic conditions of grassland - livestock

注：S(f):草地面积、B(f):单位面积可食牧草产量、P(f):单位面积草地可消化蛋白输出量、M(f):单位面积草地代谢能输出量、L(f):草地可利用率、D(f)：放牧天数、Ed:单个羊单位日需干物质量、Pd:单个羊单位日需可消化蛋白量、Md:单个羊单位日需代谢能量。Q(f):数量载畜量、DCP(f):可消化蛋白载畜量、ME(f) :代谢能载畜量。数据来源：网络资料和入户调查以及草地实测

Note:S(f):grassland area,B(f):edible grass yield per unit area,P(f):output of grassland digestible crude protein per unit area,M(f):output of grassland metabolic energy per unit area,L(f):grassland availability,D(f):number of grazing days,Ed:dry matter of a sheep units daily,Pd: digestible crude protein content of a sheep unit daily,Md:metabolic energy of a sheep unit daily.Q(f):Amount carrying capacity,DCP(f) :DCP carrying capacity,ME(f):ME carrying capacity. Sources of data:network data and household surveys,and measurement of grassland

1.2 方法

1.2.1 技术思路 草地-家畜配置的总体目标，是合理利用天然草地的前提下使经济与生态效益达到最优。依据草地资源的承载能力，结合区域特性、气候等约束条件，按照牧业生产方式和牧民生存需求合理调整种植结构，以天然草地与人工草地的可食饲草料产量、可消化蛋白输出量和代谢能输出量合理控制牲畜饲养规模，达到草地-家畜动态平衡，使大面积的天然草地得以休养生息，恢复和保护草原生态，实现草地可持续利用、生态环境良性发展和社会经济可持续发展[4]。

1.2.2 决策变量的确定 决策变量包括草地资源配置量和经济指标的发展量，具体分为草地面积S(f)、单位面积可食牧草产量B(f)、单位面积草地可消化蛋白输出量P(f)、单位面积草地代谢能输出量M(f)、草地可利用率L(f)和放牧天数D(f)、单个羊单位日需干物质量Ed、单个羊单位日需可消化蛋白量Pd、单个羊单位日需代谢能量Md；参数的选择为5年或5年以上测定的平均值。以及生态效益、经济效益。每个羊单位日需干物质量Ed是1.8 kg，单个羊单位日需可消化蛋白量Pd是0.0539 kg，单个羊单位日需代谢能量Md是8.38 MJ，粗蛋白消化率为62.25%。依据为中华人民共和国农业行业标准-天然草地合理载畜量的计算[19](NY/T635-2015)。

1.2.3 目标函数 确定目标函数，包括数量载畜量Q(f)=S(f)×B(f)×L(f)/(D(f)×Ed)，可消化蛋白载畜量DCP(f)=S(f)×P(f)×L(f)/(D(f)×Pd)，以及代谢能载畜量ME(f)=S(f)×M(f)×L(f)/(D(f)×Md)。

1.2.4 约束条件 牧草返青期是草地系统生态最脆弱的时期，是草地放牧的忌牧期，同时也是放牧牲畜的“跑青”期[1]。为避开牧草禁牧期，在牧草返青期应该舍饲。受气候影响，牧草生长期较短。因此，在草地-家畜优化配置方案中，应将返青期休牧和气候因素作为约束条件，返青期休牧(舍饲)时间为草地返青的40～60 d，放牧和转场时间应该考虑当地气候确定。

1.2.5 方案集 优化配置方案集是根据李比希(Liebig)最小因子定律[20-22]和载畜量最小的季节放牧场-关键场[17,23]，在不同季节选择关键场的草地最大理论载畜量为理论载畜量，以不同季节草地最小理论载畜量作为限制因子，优化配置不同放牧季节所缺少的部分。根据实际放牧的家畜数量和不同季节草地利用情况增减牧户家畜，由纯放牧到放牧与舍饲(返青期休牧)相结合的草畜平衡设置多组参数值，每组参数值结合目标函数和约束条件构成一个方案，多个方案组成方案集。

根据决策变量和目标函数，计算不同季节的数量载畜量，可消化蛋白载畜量以及代谢能载畜量，即Q(f)、DCP(f)和ME(f)，综合3种载畜量，确定关键场，以关键场的最大载畜量为合理载畜量。不同季节最小理论载畜量为限制因子，出现3种载畜量为限制因子的情况，根据不同情况，按照差值优化配置草地。

(1)当Q(f)为f季节牧场最小理论载畜量时，出现2种情况，分别为DCP(f)为关键场最大理论载畜量，差值X(f)=DCP(f)-Q(f)=Sf×Bf×L(f)/(Df×Ed),为了满足X(f)=DCP(f)-Q(f)，则对Sf、Bf、Df作相应的调整，分别是优化后的f季节放牧草地面积、单位面积可食牧草产量和放牧天数；或当ME(f)为关键场最大载畜量，差值X(f)=ME(f)-Q(f)=Sf×Bf×L(f)/(Df×Ed),为了满足X(f)=ME(f)-Q(f)，则对Sf、Bf、Df作相应的调整，即为调整后的f季节放牧草地面积、单位面积可食牧草产量和放牧天数。

调整方案为增加f季节草地放牧面积，或增加可食牧草产量，或调整放牧时间。增加f季节草地放牧面积可通过将其他季节放牧草地面积划分为f季节放牧，划分方式为冬春牧场部分划分到夏季牧场或秋季牧场，冬春牧场缺少部分用人工草地代替；增加可食牧草产量的途径有秃斑地补播，改良原来牧场；调整放牧时间的途径有增加或缩短f季节放牧时间或调整舍饲时间。

(2)当ME(f)为f季节牧场最小载畜量时,出现2种情况，分别为DCP(f)为关键场最大载畜量，差值X(f)=DCP(f)-ME(f)=Sf×Mf×L(f)/(Df×Ed),为了满足X(f)=DCP(f)-ME(f)，则对Sf、Mf、Df作相应的调整，分别是为调整后的f季节放牧草地面积、单位面积草地代谢能输出量和放牧天数；或当Q(f)为关键场最大载畜量，差值X(f)=Q(f)-ME(f)=Sf×Mf×L(f)/(Df×Md),为了满足X(f)=Q(f)-ME(f)，则对Sf、Mf、Df作相应的调整，即为调整后的f季节放牧草地面积、单位面积草地代谢能输出量和放牧天数。

调整方案为增加f季节草地放牧面积；或增加草地代谢能输出量；或调整放牧时间；增加f季节草地放牧面积可通过将其他季节放牧草地面积划分为f季节放牧，划分方式为冬春牧场部分划分为夏季牧场或秋季牧场，冬春牧场缺少部分用人工草地代替；增加草地代谢能输出量的途径有补播优良草种改良天然草地，购买饲草料；调整放牧时间的途径有适当增加或缩短f季节放牧时间或调整舍饲时间。

(3)当DCP(f)为f季节牧场最小载畜量时,出现2种情况，分别为Q(f)为关键场最大载畜量，差值X(f)=Q(f)-DCP(f)=Sf×Pf×L(f)/(Df×Pd),为了满足X(f)=Q(f)-DCP(f)，则对Sf、Pf、Df作相应的调整，分别是调整后的f季节放牧草地面积、单位面积草地粗蛋白输出量和放牧天数；或当ME(f)为关键场最大载畜量，差值X(f)=ME(f)-DCP(f)=Sf×Pf×L(f)/(Df×Pd),为了满足X(f)=ME(f)-DCP(f)，则对Sf、Pf、Df作相应的调整，即为调整后的f季节放牧草地面积、单位面积草地粗蛋白输出量和放牧天数。

调整方案为增加f季节草地放牧面积；或增加草地粗蛋白输出量；或延长放牧时间；增加f季节草地放牧面积可通过将其他季节放牧草地面积划分为f季节放牧，划分方式为冬春牧场部分划分为夏季牧场或秋季牧场，冬春牧场缺少部分用人工草地代替；增加草地粗蛋白输出量的途径有草地补播优良草种，购买饲草料，补充高蛋白精料；调整放牧时间的途径有增加或缩短f季节放牧时间。

1.2.6 各方案效益的计算 方案的效益根据以下公式确定：

Fc(f)=Max(Em(f)+Eg(f))

式中Fc(f)、Em(f)、Eg(f)分别为f季节的综合效益、经济效益和生态效益的增量；

经济效益增量Em(f)通过以下公式确定：

式中R(i),Y(i)分别为方案调整前i类产品的产量和单价，C(j)为方案调整前j类产品发生的费用；Ra(i),Ya(i)分别为方案调整后i类产品的产量和单价，Ca(j)为方案调整后j类产品发生的费用；

i表示家畜、肉、奶、皮毛、酥油；所述j可表示为购买饲草的费用、种子费、运输费、防疫费、人工草地收割费；

生态效益增量Eg(f)通过以下公式确定：

Eg(f)=∑(A1+A2+A3+A4)

式中A1,A2,A3,A4分别为f季节草地利用变化率，可食牧草利用变化率，草地载畜量变化率和害情发生变化率；

A1,A2,A3,A4通过以下公式确定：

式中Gb，Ga分别为调整后草地可利用面积和调整前草地可利用面积；

式中Fb，Fa分别为调整后单位面积可食牧草的产量和调整前单位面积可食牧草的产量；

式中Sb，Sa分别为调整后草地载畜量和调整前草地载畜量；

式中Rb，Ra分别为调整后草地害情发生面积和调整前草地害情发生面积。

根据不同优化配置方案计算各方案的经济效益和生态效益，综合两者，选择综合效益最大的方案作为不同季节配置的最佳方案。

2 结果与分析

2.1 牧户草地-家畜优化配置方案集

根据调查与实测数据，输入决策变量，季节草场的草地面积S(f)、单位面积可食牧草产量B(f)、单位面积草地蛋白输出量P(f)、单位面积草地代谢能输出量M(f)、草地可利用率L(f)和放牧天数D(f)、单个羊单位日需干物质量Ed、单个羊单位日需可消化蛋白量Pd、单个羊单位日需代谢能量Md；根据输入的变量计算不同季节的3种载畜量。确定约束条件，为返青期休牧，根据地域、气候、水热条件等确定该牧户家畜补饲时间为5月20日至6月底(40 d)。

根据载畜量最小的季节放牧场确定关键场，该牧户的关键场是夏季牧场，关键场的草地最大理论载畜量是可消化蛋白载畜量DCP(f)，根据李比希(Liebig)最小因子定律，确定夏季牧场草地最小理论载畜量是数量载畜量Q(f)，秋季牧场草地最小理论载畜量是代谢能载畜量M(f)，冬春季牧场草地最小理论载畜量是可消化蛋白载畜量DCP(f)。按照差值优化配置草地，形成8个可选方案(表3)。根据不同方案集，结合收益与成本计算各个方案的经济效益和生态效益并求得综合效益(表3)。

2.2 配置结果

根据关键场最大载畜量确定该牧户理论载畜量为418个羊单位，按照方案1，2，3对夏季牧场草地进行配置，方案1为草地单位面积增产1 136 kg·hm-2。根据气候因素确定约束条件为返青期休牧40 d，则需要8.1 hm2的人工草地，该牧户原来有6.7 hm2的人工草地，由于该牧户的冬春草地为沼泽草甸，夏季牧场为高寒草甸，因此，方案2为划分原有夏季牧场草地1.4 hm2用来种植人工草地，再划分5.4 hm2的冬春牧场为夏季放牧所用，方案3为延长夏季放牧时间为97 d。根据不同方案对综合效益进行计算，得到方案1，2，3的经济效益分别提高了-84.4%，6.7%和-24.7%，生态效益分别提高了31.7%，5.1%和-16.5%，结合两者得到综合效益分别提高了-52.7%，11.8%和-41.2%。

按照方案4、5、6对秋季牧场草地进行配置，分别为减畜到418个羊单位，草地部分不做调整；在方案3的基础上调整放牧时间为10月6日-11月26日；根据载畜量计算延长放牧时间为55 d。根据不同方案对综合效益进行计算，得到方案4、5、6的经济效益分别提高了18.3%，-4.1%和16.7%，生态效益分别提高了9.5%，-11.4%和8.6%，结合两者得到综合效益分别提高了27.8%，-15.5%和25.3%。

按照方案7、8对冬春季牧场草地进行配置，方案7，8是基于方案4和6做了调整，方案7为放牧时间缩短到212 d，需购精料补充蛋白；方案8调整是放牧时间缩短到209 d，需购精料补充蛋白。根据不同方案对综合效益进行计算，得到方案7，8的经济效益分别提高了5.0%和5.1%，生态效益分别提高了22.3%和22.7%，结合两者得到综合效益分别提高了27.3%和27.8%。

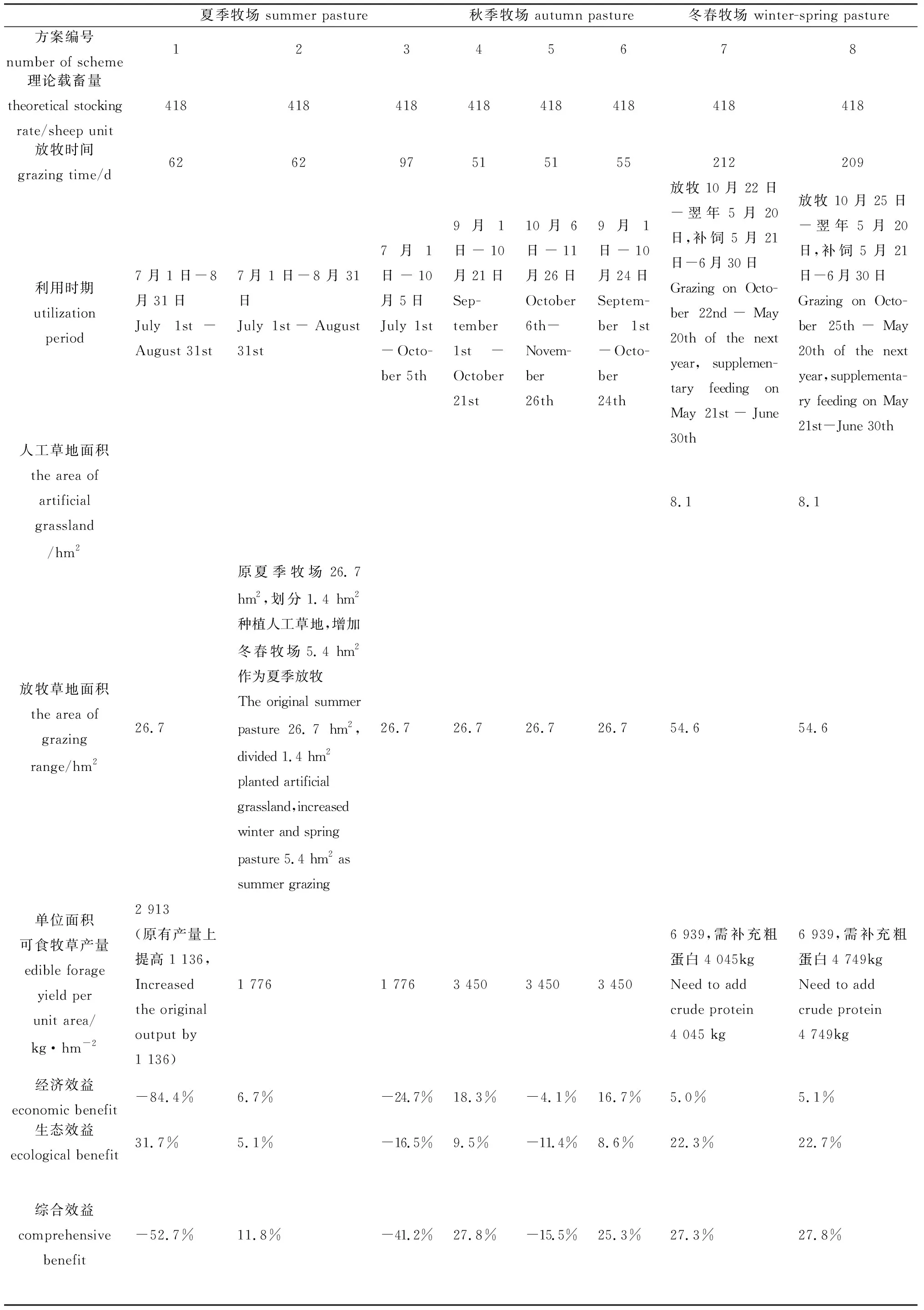
表3 牧户草地-家畜调控方案及效益Table 3 Herdsmen grassland-livestock control program and benefit

3 讨论

实现草畜平衡制度受到很多因素的制约，虽然合理的草地载畜量严格地受到国家政策的规定，但是牧民为了提高经济收入，会根据自己的劳动力状况和经济条件不断扩大放牧家畜的规模和数量，而忽略了草地的生态状况。或是牧民为了避免超载的惩罚而利用增加科技、资金投入等方式提高天然草原的产草量，更多地将天然草地生态系统转变为栽培草地生态系统，威胁到草地生态经济系统的弹性[24]，造成不超载情况下的过牧，影响草地生态系统的可持续发展[24-25]。一味地“减畜”和开垦对草地生态系统和牧民的经济利益都会造成很大的威胁，李艳波等[26]也提出，仅靠控制牲畜数量不能实现草畜平衡。

针对草地-家畜资源开发利用特点，本研究构建了适宜的草畜平衡优化配置模型。根据李比希(Liebig)最小因子定律和关键场[17-22]，结合返青期休牧、人工草地舍饲喂养，以一牧户为例，对其草地-家畜配置进行了合理优化。根据输入参数和目标函数以及约束条件对不同季节牧场进行优化配置，计算可得该牧户的关键场为夏季牧场，最大载畜量为可消化蛋白载畜量，为418个羊单位。考虑到草地承载力，家畜单位应从现有的520个羊单位减到418个羊单位。本研究中，在夏季放牧地的营养载畜量(包括DCP和ME载畜量)均高于数量载畜量，并且DCP载畜量高于ME载畜量，这与郝力壮等[27]暖季(7-8月牧草)在玛多县的研究结果一致。

根据载畜量设置优化配置方案，夏季牧场配置方案分别为1，2，3方案，根据配置方案计算生态效益和经济效益，综合可得综合效益，三种方案中方案2的综合效益最大，是11.8%，虽然方案1的生态效益最大，但改良草地发生的费用较大，经济效益为负增长。延长放牧时间对草地的利用时间太长，由于草地本身产草量低及当地气候限制，牧草的生长季较短，不能满足家畜采食，对经济效益和生态效益均起下降作用，因此，方案3的综合效益仍为负增长。另外，该牧户秋季牧场最小载畜量为455，满足关键场载畜量要求，结合草地资源，秋季牧场可满足418个羊单位放牧55 d，所以方案6将放牧时间延长为55 d，方案4除了减畜外不做其他调整，方案5是根据夏季牧场方案3作调整，将放牧时期调整为10月6日-11月26日。根据配置方案得到综合效益增量分别为27.8%，-15.5%和25.3%，结合地域和气候，延后秋季放牧时间对草地生态和牧民经济效益没有增加反而下降，这与赛希雅拉对内蒙古天然草原草畜平衡管理政策实证研究结果一致，在气候变化剧烈的系统，采用固定的或保守的载畜量不仅不合适，而且对于牧民来说成本也很高[28]。

牧草返青期是草地系统生态最脆弱的时期，也因此被称为高寒牧区天然草地的“忌牧期”[3]。研究表明春季休牧可以有效改善草地植被群落，抑制毒草生长，有效控制鼠害[29]，被证明是畜牧业发展和草地生态保护兼顾的一项有效措施[30-32]。因此，在优化配置方案中我们考虑了返青期休牧，对冬春季牧场优化配置方案为7和8，为返青期休牧40 d(补饲5月21日-6月底)舍饲喂养，所需人工草地除了原来的6.7 hm2外，划分夏季牧场1.4 hm2用来种植人工草地，则原来的冬春季牧场草地面积调整为54.6 hm2，方案7和方案8的放牧时间分别为212 d和209 d。由于冬季牧草粗蛋白含量低，不能满足家畜营养需求，因此，需购买精料补充蛋白所需。根据配置方案7和8，计算综合效益增量分别27.3%和27.8%。

牧草的生长除了本身特性外还受地区气候因素的影响[33-36]。本研究中试验地位于高寒牧区，返青期从5月中下旬开始，返青期牧草产量增长速度较快，随着青草期雨季的到来，水热条件的影响逐渐增大，牧草产量增长速度减慢，青草期牧草产量达到最大，进入枯草期(9月份之后)，牧草枯黄，生物量积累呈现负值[37-38]。因此，在本次配置实例中，根据综合效益及区域气候因素，我们选择的优化配置方案为2，4和7。

本研究构建了适于牧户的草地-家畜优化配置模型，为草地健康发展及牧民增收提供了参考依据。但牧场草畜平衡调控研究仍处于起步阶段，其调控理论、方法应结合牧场实际情况及当地区域气候作进一步的修正，优化配置方案仍需要在实践检验中进行逐步探索和完善。另外，高寒草地害鼠种群密度很高，下一步的草地-家畜配置应考虑将害鼠控制到某一经济水平或生态阈值。

4 结论

本文通过对草地-家畜优化配置的研究，构建了适宜的草畜平衡优化配置模型。根据李比希(Liebig)最小因子定律和关键场计算，得出玛沁县1牧户的理论载畜量为418个羊单位，相比优化配置前，载畜量减少了102个羊单位。结合经济效益和生态效益最大化，得出该牧户3季牧场优化配置的3种最佳方案，分别为划分冬春季牧场5.4 hm2用于夏季放牧；秋季牧场在数量和营养上都满足家畜的需求进而不做调整；和冬春牧场放牧212 d，舍饲40 d(5月21日-6月底)，由于冬春季饲草丰裕但营养不足，则需购买精料补充家畜营养。3种方案下综合效益可分别提高11.8%，27.8%和27.8%。在草地承载力范围内，返青期休牧40 d，经济效益和生态效益分别增加了5.0%和22.5%。