岩体结构面模拟的统计方法改进研究
2019-07-25张斌,黄俊
张 斌,黄 俊
(1.中国华西工程设计建设有限公司,四川成都610031;2.地质灾害防治与地质环境保护国家重点实验室(成都理工大学),四川成都610059)
0 引 言
岩体是由岩块及结构面组成的非均质不连续体,而岩体中结构面的几何特征、组合特征较为复杂,使岩体结构表现出一定的复杂性[1-3]。目前,针对岩体结构面几何特性的研究,已经取得了许多成果,但是仍然存在些许不足。在结构面三维网络模拟过程中,需对采集的数据进行合理分组,然后对每组数据建立概率模型[4]。上述过程中,对结构面的分组没有定量标准,一般根据数据整体分布趋势进行分组,主要通过极点分布图或直方图[5- 8],而在直方图统计中,带宽的确定通常也是依经验而定,对同一组数据的特征,不同带宽的直方图的反映是不同的。因此,需要一种定量确定带宽的方法,提高直方图统计的可靠性。其次,对结构面要素的分布类型的判定过于依靠经验,卡方检验[9-10]是一种很好的方法,但其操作过于复杂,极大似然估计相对简便。此外,还是有一个无法回避的问题,即结构面不能完全服从目前已知分布,甚至相差很大。在非参数估计方法中,核密度估计方法[11]在样本不能较好服从已知分布的情况下,可以模拟得到与样本较一致的随机数。
鉴于此,本文针对目前结构面模拟中存在的问题,利用现场采集的结构面数据,使用定量方法确定结构面要素的分布类型及数据带宽,通过核密度估计方法提高结构面模拟精度,并针对传统蒙特卡洛方法,提出了新的工作思路,以简化工作流程。
1 研究区概况
本文采集数据源于我国西南某在建大型水电站坝基右岸岩体(见图1)。该水电站坝址位于金沙江下游,高原深谷地貌,呈不对称“V”字形峡谷。右岸为药山山脉西坡,山峰高程在3 000 m以上,主要为陡坡与缓坡相间的地形。金沙江由南向北流入坝区,枯水期水面宽50~115 m,水位约594 m,水深9~18 m不等。拱坝部位高程825 m处谷宽590~713 m。研究区域主要出露二叠系上统峨眉山组柱状节理玄武岩,采用测线法对坝基岩体进行结构面精测,得到结构面极点分布,见图2。

图1 右岸建基面岩体
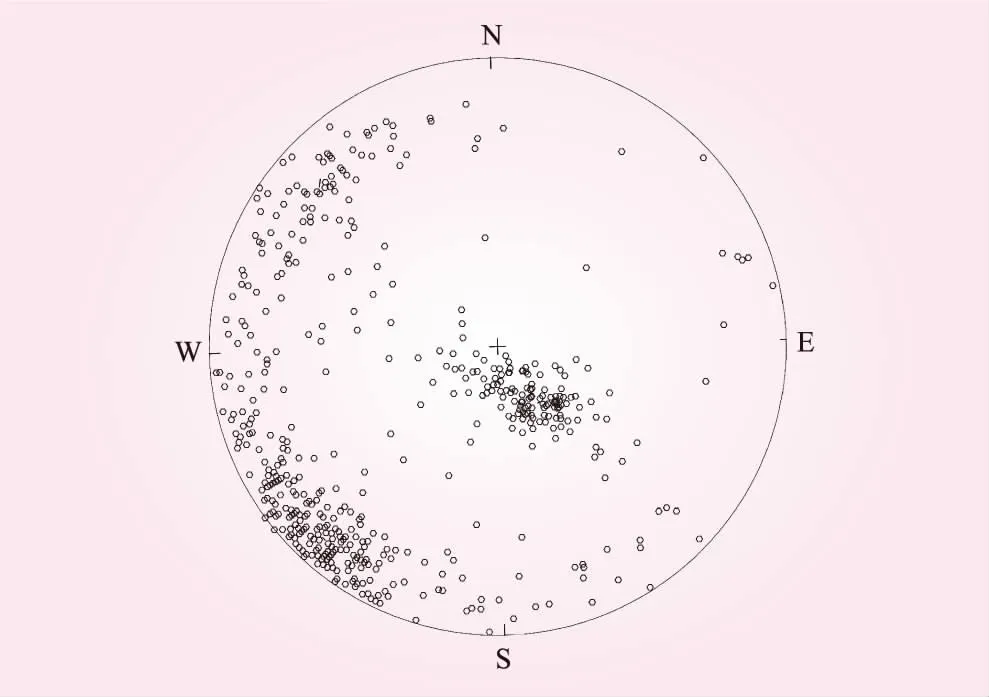
图2 结构面极点分布
2 结构面模拟的蒙特卡洛方法
2.1 方法介绍
蒙特卡洛方法(Monte Carlo method)可以用来解决具有概率解释的任何问题,因其求解的问题本身具有内在的随机性,因此必须借助计算机的运算能力才能模拟这种随机的过程。在研究具有概率解释的问题时,对随机数抽样,使抽样结果符合问题的分布形式,从而对研究的问题进行模拟。由于需要大量随机数,蒙特卡洛方法必须依赖于计算机。尽管岩体结构面是随机分布的,但经验表明,结构面的空间分布在一定条件下依然符合一定的概率分布。因此,对精测数据使用蒙特卡洛方法,便可得到一定深度范围内的结构面特征数据。
2.2 工作流程
使用蒙特卡洛方法对结构面进行三维模拟,首先要判定数据所服从的分布类型,然后生成服从该分布的随机数[12]。由于岩体受到不同时期不同类型构造的影响,整体不易服从某一确定的分布,所以根据直方图起伏和集中趋势对数据进行分组,每组数据单独使用蒙特卡洛方法模拟。需要注意的是,每组数据在使用蒙特卡洛方法前后,其在数据总量中所占的比值应保持一致。
2.3 直方图统计的带宽优化
带宽在直方图统计中是一个自由参数,一般根据经验确定。直方图统计是一种对未知量的非参数估计。直方图中,带宽过大或过小,得到的直方图都不能反映问题的真实情况。带宽过大,造成直方图过于平滑,易忽略细节;带宽过小,放大了细节在直方图中的作用,得到的直方图会产生较多的尖刺,增加了异常的比重,也不能较好地反映真实情况。因此,带宽是否取值得当直接决定了直方图统计的质量,影响后续论述。为量化带宽的选取是否得当,需要一个误差函数来衡量,本文使用平均积分平方误差(MISE)作为带宽选取的误差,平均积分平方误差MISE表达式为[12-13]
(1)
式中,f(x)为未知的真实的密度分布;fh(x)为基于样品的以带宽h为独立变量的假定分布;E是样本的期望。
由于密度函数f(x)未知,无法直接得到方程的解,可通过计算机的多次计算,寻找该式的最小值,从而代替直接求解方程[14]。本文使用上述方法编写的程序对带宽进行优化,倾角优化后的最佳带宽为1.72,倾向为7.06,迹长为0.060 232 7,相对应的最佳区间数分别为52、51和50。
2.4 结构面要素的分布拟合优度检验
使用带宽优化之后的数据进行直方图统计(见图3),结果与极点分布图保持一致,能够均衡地反映结构面的优势产状和发育较弱的产状。经过带宽优化的直方图,降低了主观因素对直方图趋势的影响。依据统计结果对数据进行分组,根据数据的峰值和起伏状况,将倾角分为[0°, 50°)和[50°, 90°]2个组,倾向分为[0°, 180°)、[180°, 280°)和[280°, 360°]3个组,迹长不分组。

图3 结构面要素统计直方图
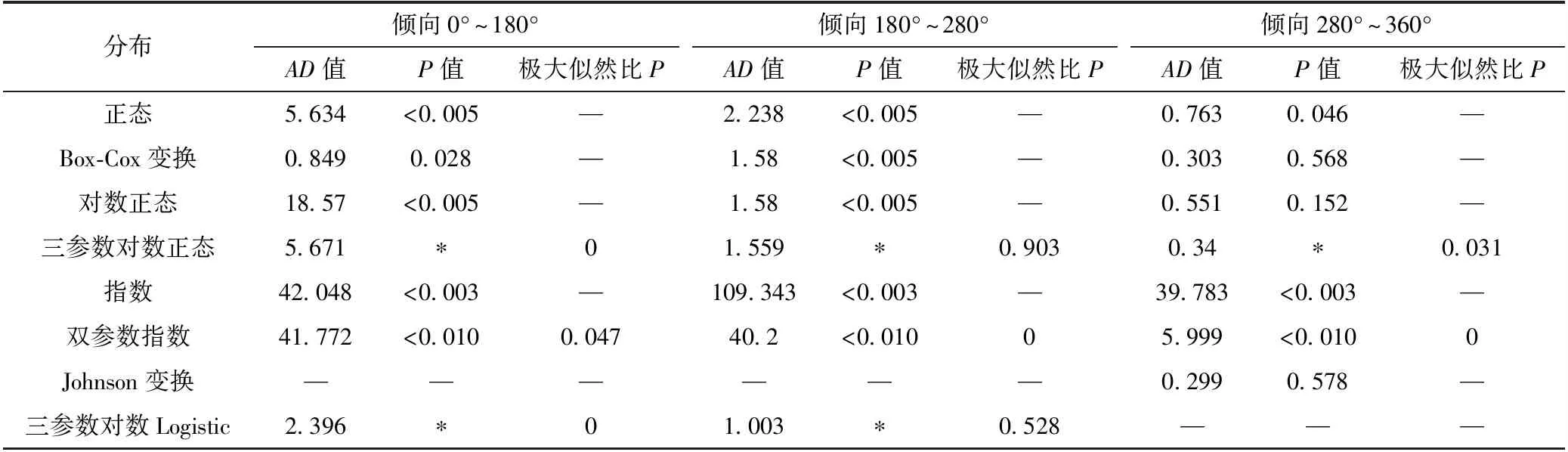
分布倾向0°~180°AD值P值极大似然比P倾向180°~280°AD值P值极大似然比P倾向280°~360°AD值P值极大似然比P正态5.634<0.005—2.238<0.005—0.7630.046—Box-Cox变换0.8490.028—1.58<0.005—0.3030.568—对数正态18.57<0.005—1.58<0.005—0.5510.152—三参数对数正态5.671∗01.559∗0.9030.34∗0.031指数42.048<0.003—109.343<0.003—39.783<0.003—双参数指数41.772<0.0100.04740.2<0.01005.999<0.0100Johnson变换——————0.2990.578—三参数对数Logistic2.396∗01.003∗0.528———
对结构面数据进行分组后,分别对每组数据进行参数估计,使用Minitab进行分布类型检验。本文使用Anderson-Darling检验(简称“AD检验”)进行极大似然估计(当能够进行似然比检验时显示极大似然比P,P值是一个概率,用来度量否定原假设的证据)。Anderson-Darling统计量(即AD值,表示假定分布与样本的差值的平方)用来衡量数据遵循特定分布的程度。对指定的样本和分布,分布越适合样本,AD值越小,其表达式为[15]
(2)
式中,n是样本数;f(x)是待检验的假定分布;fh(x)为样本的累积分布函数。本文使用相应的P值(当存在时)来检验数据是否服从假定分布。如果P值小于选定的阈值α(本文取0.05,但0.05只是一个常用的阈值,P值小于0.05并不是无效假设,只能说明其拒绝原假设的理由更充分),则拒绝数据来自该分布的假设。P值在数学上不存在时,Minitab软件就不显示AD检验的P值。对研究区结构面要素进行分布拟合优度检验,得到结构面要素的概率分布图(默认置信区间为95%)。对6组数据进行分布类型检验后的结果见表1~3。表中, *表示无法计算的缺失值。

表1 倾角分布类型检验结果
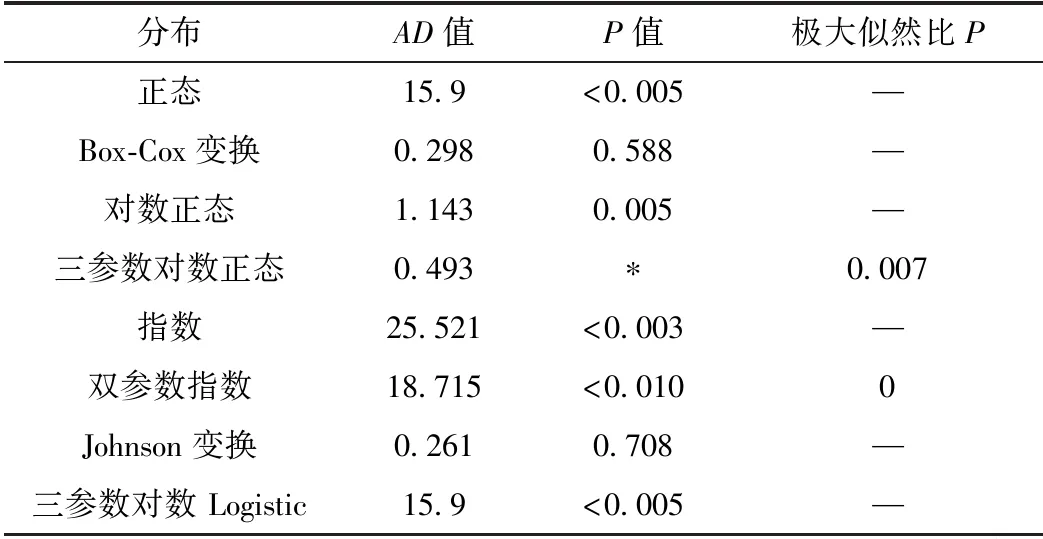
表3 迹长分布类型检验结果
综合AD值小、P值大的原则,确定原数据分布类型。其中,倾向0°~180°区间较符合Box-Cox变换后正态分布,倾向180°~280°区间较符合三参数对数正态分布,倾向280°~360°区间较符合Johnson 变换后正态分布;倾角0°~50°区间较符合Box-Cox变换后正态分布,倾角50°~90°区间较符合Box-Cox变换后正态分布;迹长服从Johnson变换后正态分布。各自对应的在95%置信区间的累积概率分布见图4~6。

图4 倾角累积概率分布
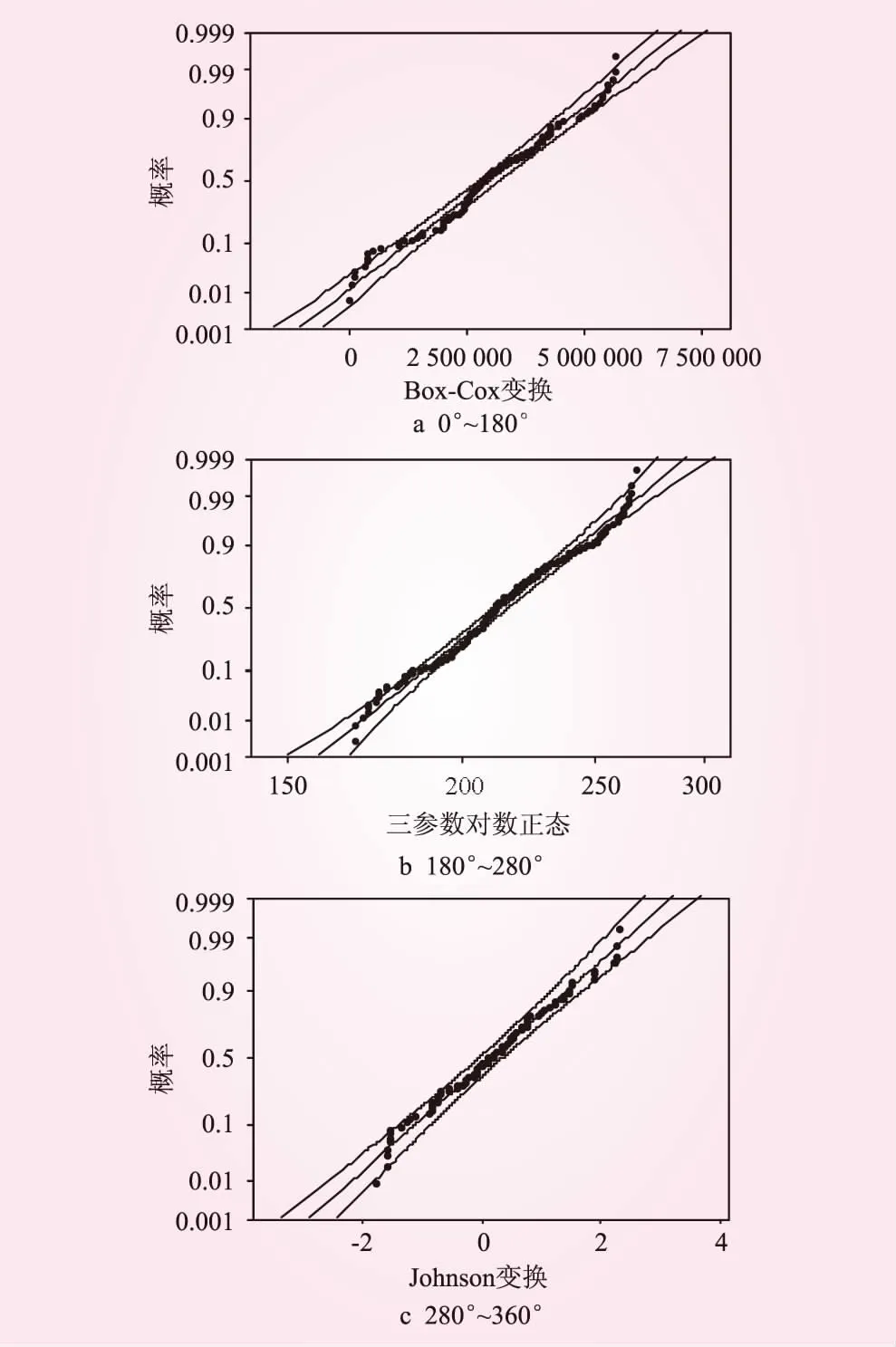
图5 倾向累积概率分布

图6 迹长累积概率分布
分布拟合优度检验结果表明,仅迹长在未经分组的情况下,对假定分布类型的接受程度较高。岩体作为非均质体存在,在各种地质营力的作用下,被结构面切割,在一定区域内形成几何相似的块体,因此在统计量没有大到足以代表整个岩体结构面时,精测数据应该是非连续数据。在特定地质营力作用下,形成的数量相对较多、且易于被观察和测量的部分结构面,即为优势结构面。优势结构面数量较大,易于被观测,因此优势结构面数据在精测数据占比较大。林德伯格-费勒中心极限定理亦表明,结构面迹长作为描述结构面出露程度的标量,其原始数据(未分组)应该服从正态分布。
2.5 模拟结果
本次模拟在Jupyter notebook中完成。Jupyterno-tebook是基于Python的交互式解释器。整个程序设计过程为:首先,程序初始化后导入数据,设置并初始化变量,对数据分组;然后,确定模拟的各组数据的总量,根据各组数据对应的变换方式分别对每组数据进行变换,使用NumPy工具库生成伪随机数,接着对生成的伪随机数反变换,得到模拟结果,见图7。
对比图3,使用蒙特卡洛方法模拟的结果,在集散趋势上与原数据保持一致。经过带宽优化后,为避免主观因素的影响,使用量化方法判断精测数据的分布类型。通过分布类型检验,获得了数据的一般分布类型,但由于细节的损失,模拟结果无法较好再现原数据的分布特征。

图7 模拟结果直方图

图8 原始数据与核密度估计结果对比
3 结构面模拟的核密度估计
使用蒙特卡洛方法进行结构面模拟时,需要对数据进行分布类型检验,而模拟结果的好坏取决于数据对假定分布类型的服从程度。对数据切割分组的不连续,可能降低模拟结果的准确性。为提高模拟结果与原始数据的相似度,使用核密度估计方法对结构面数据进行模拟。
3.1 核密度估计
核密度估计是估计随机变量的概率密度函数的非参数方法,这意味对随机变量的估计不再需要固定的参数,而且程序设计可以减少很多工作。在直方图统计中,对于区间(xk-1,xk]((xk-1,x]为其中某1个条带)中的所有样本都同等对待。如在[0,1]区间,有2个样本取值0+和1-,前者表达的信息是分布在0周围有密度,而后者应该在1周围有密度,两者存在不同的含义。因此,对于直方图统计,给定宽度h,样本Xi应该反应区间[Xi-h/2,Xi+h/2](该区间的分布函数为I(-h/2≤x≤h/2))的信息,定义[16]
Kh(x)=I(-h/2≤x≤h/2)/h
(3)
对应的估计fh(x)为
(4)
再进一步把宽度h看成参数,直接定义K(x)=I(|x|≤1)/2,若该区间的权重相等,则估计fh(x)为
(5)
(6)
Kh(· )=K(·/h)/h称为核函数,理论上任何非负单峰的概率密度函数都可以作为核函数。不同的核函数在对目标进行核密度估计时会产生不同估计模型,在每个估计区间体现核函数原本的性质。目前,常用的核函数是高斯(Gaussian)核函数,表示为K(x;h)∝exp[-x2/2h2]。
3.2 结构面模拟的核密度估计
使用核密度估计方法,依然要先对数据进行带宽优化。使用优化后的带宽,在Jupyter notebook中,利用Scikit-learn工具计算。为提高采样精度,Scikit-learn中的KDE模块引入了最近邻算法中的KDTree和BallTree,使采样模型更贴近原始数据。使用Gaussian内核的核密度估计方法对精测数据模拟。原始数据与核密度估计结果对比见图8。图8中,直方图为原始数据统计结果,曲线为核密度估计。核密度估计模拟结果见图9。
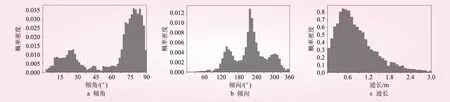
图9 核密度估计模拟结果
3.3 结果对比
从图8可知,高斯内核的核密度估计曲线较为平滑,其概率密度的变化均为渐变曲线。而直方图统计中,相邻区首尾相接处的数据是跃变的,而实际上在区间连接处数据应该是连续的。因此,使用核密度估计方法对数据进行统计,能够提高模拟的精度。核密度估计曲线与直方图统计数据增减趋势一致,但不完全贴近方块,为模拟结果预留了变化区间,表明核密度估计的结果受偶然因素的影响较小,可以减少过拟合的发生。在保证带宽为最佳的前提下,使用核密度估计既能够保留细部特征,又能够兼顾整体分布趋势。
从图9可知,对比原始数据和蒙特卡洛方法的结果,核密度估计结果更符合原始数据的集散趋势,并且对细部的反映更真实。观察蒙特卡洛模拟结果,其数据整体较为规律,数据的整体分布趋势符合公式生成数据的特点。而核密度估计方法模拟的结果更加贴近原数据方块。在整体趋势上,两者的结果较为相似,但在局部数据的呈现上,核密度估计更加符合原数据的特点,对细节的把握更充分。
在工作流程上,蒙特卡洛方法的工作量更大,实施步骤更多。核密度估计只需要进行带宽优化、直方图统计、核密度估计、随机数生成,最后成果检验,相对而言,工作量大大减少。从量化的角度看,蒙特卡洛方法在分组时存在主观判断,可能对模拟的成果有一定影响。因此,在结构面三维模拟中,使用核密度估计方法,有利于模拟精度的提高,同时减少工作量。
4 结 语
本文以西南某大型在建水电站建基面结构面精测数据为基础,对结构面要素进行统计分析,使用平均积分平方误差优化直方图统计带宽。引入核密度估计方法,对结构面模拟的统计方法进行改进,对比蒙特卡洛方法的流程和结果,得出以下结论:
(1)使用平均积分平方误差对直方图带宽进行优化后,直方图统计结果与极点分布图保持一致,能够照顾到结构面的优势产状和发育较弱的产状。经过带宽优化的直方图,能避免主观因素对直方图的影响,为结构面分布类型的确定和核密度估计做好铺垫。
(2)在蒙特卡洛模拟中,采用了极大似然估计,根据各组数据对应的AD值和P值,判定各组数据对假定分布类型的服从程度,从而确定分布类型。蒙特卡洛方法的结果表明,其把握数据的整体分布趋势较好,但细节丢失严重。
(3)在探索提升结构面模拟精度的过程中,引入核密度估计方法,结果表明,其结果能够较好地还原数据的整体分布特征。此方法省略了分布类型检验等步骤,忽略了主观因素对结果的影响,提高了模拟精度,减少了工作量。
