基于Elman网络和实时递归学习的洪水预报研究
2019-07-25万新宇华丽娟孙淼焱钟平安
万新宇,华丽娟,孙淼焱,钟平安
(河海大学水文水资源学院,江苏南京210098)
我国洪涝灾害发生频繁,经济损失巨大[1]。准确预报洪水过程是减轻洪水灾害的一项重要的非工程措施[2]。目前,洪水预报方法较多,大体可分为模型驱动与数据驱动两类。模型驱动利用各类基于物理机制的水文模型进行洪水预报,如新安江模型[3]、TOPKAPI模型[4]和TOPMODEL[5]等。此类模型能详细描述流域洪水形成过程,预报精度高,应用广泛;但对资料要求高,除了基本的降雨径流资料外,还需要流域蒸发、地形地貌和土地利用等资料的支撑[6]。当资料要求得不到满足时,人们常常依据统计理论构建降雨径流数据驱动模型,如ARMA[7]、NARX[8]和神经网络模型[9]等。其中,以神经网络模型应用最为流行。
神经网络模型一般分为静态网络和动态网络[10]。静态网络主要有反向传播网络[11]、径向基网络[12]和广义回归网络[13]等。其中,以应用反向传播网络进行洪水预报最为普遍[14-15]。然而,流域洪水过程是一个复杂的非线性的动态过程,当前时刻洪水流量受到前期若干时段的降雨、径流以及流域状态的影响,静态网络一般难以反映这种动态特征[16]。相反,动态网络因具有反馈连接和延迟结构而能够反映系统的动态变化过程,如Elman网络[17,18]和NARX网络[19]。为此,本文以淮河流域响洪甸水库为例,基于Elman网络构建洪水预报模型,采用实时递归学习算法进行模型训练,并对模型预测性能进行评价。
1 研究方法
1.1 Elman动态网络
本研究基于三层感知机,构建动态神经网络,其中包含1个输入-输出联结层、1个隐含层和1个输出层,具体结构如图1所示。网络有M个外部输入和K个输出。x(t)为网络在t时刻的M×1维外部输入向量,z(t+1)为网络在t+1时刻的K×1维输出向量,y(t+1)为网络在t+1时刻隐含层的N×1维输出向量。联结外部输入向量x(t)和隐含层延迟输出向量y(t),得(M+N)×1维向量u(t),其中ui(t)代表其第i个元素,即
(1)
式中,A为外部输入xi(t)的下标集;B为隐含层单元输出yi(t)的下标集。
网络的输入-输出联结层与隐含层之间完全互连,其中有M×N个前向连接和N×N个反馈连接。W表示网络的N×(M+N)维递归权重矩阵。为了使每个单元都有一个偏置值,本研究在M个输入中总包含一个值为1的输入。隐含层与输出层也是完全互连,V表示K×N维权重矩阵。
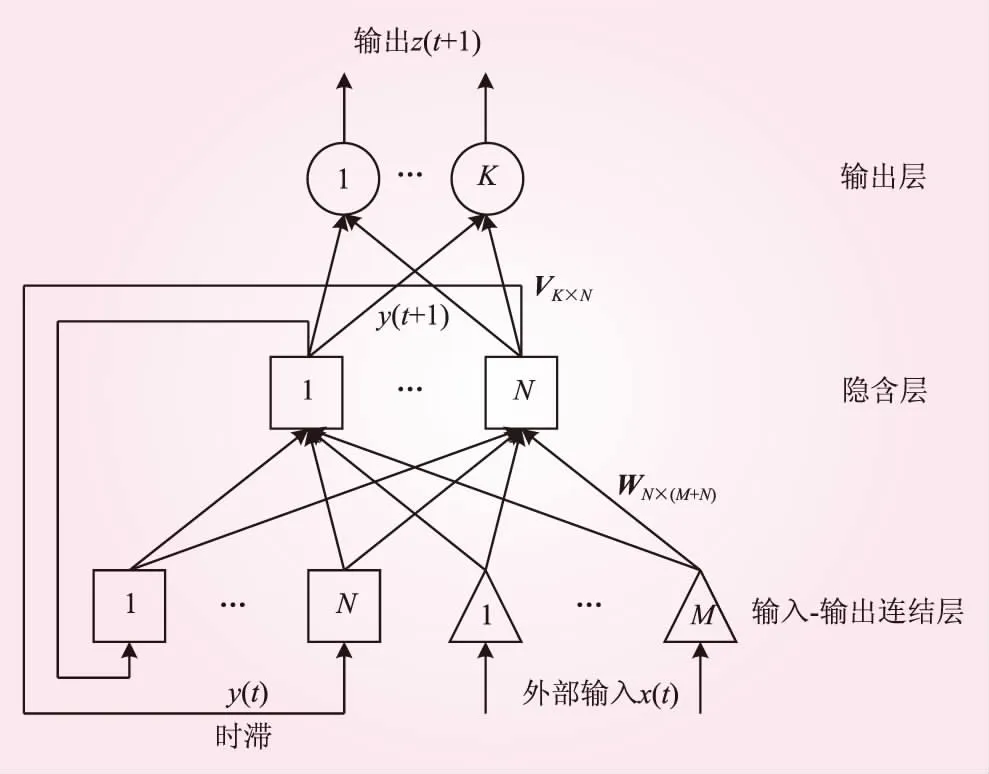
图1 Elman动态网络结构
计算t时刻网络隐含层中神经元j的净输入,j∈B。即
(2)
再由传输函数f1(·)得到隐含层神经元j在t+1时刻的输出,即
yj(t+1)=f1(netj(t))
(3)
计算网络输出层神经元k在t+1时刻的净输入netk(t+1)和输出zk(t+1)。即
(4)
zk(t+1)=f2(netk(t+1))
(5)
式中,f2(·)为隐含层到输出层的传输函数。值得注意的是,t时刻的外部输入直到t+1时刻才会影响神经元的输出。上述系统构成完整的动态网络,本研究中传输函数f1(·)和f2(·)分别取tanh函数和线性函数。
1.2 性能函数
定义t时刻的网络输出K×1维时变误差向量e(t),其第k个元素为
ek(t)=dk(t)-zk(t)
(6)
式中,dk(t)为t时刻输出层神经元k的目标值。定义网络t时刻的瞬时误差平方和为
(7)
则网络所有时刻的总误差为
(8)
1.3 实时递归学习算法
(9)
(10)
式中,η2为学习参数。又有
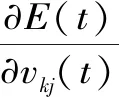
(11)
同理,可以求得各时刻权重wmn的变化
(12)
式中,η1是学习参数。
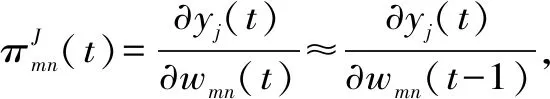
(13)
(14)
式中,j∈B,m∈B,n∈A∪B;δmj为克罗内克函数,当且仅当j=m时,δmj=1;否则,等于0。
假设时刻时t=0网络的初始状态与其权重无关,即
(15)
利用实时递归学习算法训练如图1所示Elman动态网络,步骤如下:
(1)从开始,对每一时刻,用网络的动态方程式(2)和(3)计算隐含层N个神经元的输出,从而求出联合输入ui(t)(i∈A∪B);再用动态方程式(4)和(5)计算输出层K个神经元的输出。对权重的初值可赋以均匀分布的随机数。
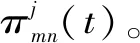
(16)
(4)按式(17)修正权重wmn和vkj
(17)
重复上述计算,直到误差满足一定的精度。
上述方法中,从初始时刻开始,每一时刻修正一次权重,使用的是瞬时误差的梯度,与总误差的梯度不同。当学习参数较小时,两者效果差别不大[20]。
2 研究实例
2.1 流域与水库概况
本研究以响洪甸水库为例,进行入库洪水预报研究。响洪甸水库位于大别山区淮河流域淠河西源的安徽省金寨县境内,流域面积1 431 km2。上游主要支流有燕子河、宋家河、姜家河,其中燕子河经张冲流入水库,宋家河和姜家河在青山汇合后流入库内。流域设有5座雨量站和2座水文站,具体分布如图2所示。流域内地势南高北低,均是山区坡地汇流,汇流时间短。地质构造简单,以水成变质岩分布最广,其次为火成变质岩和火山岩。流域内植被较好,多为野生灌木丛。地表面与岩面覆盖层一般为0.5 m左右,渗透性较好。响洪甸水库地处江淮之间,位置偏南,气候接近长江流域。降雨主要受季风控制,多年平均降水量1 519.8 mm,7、8月降雨频繁且雨量大,易造成洪水。
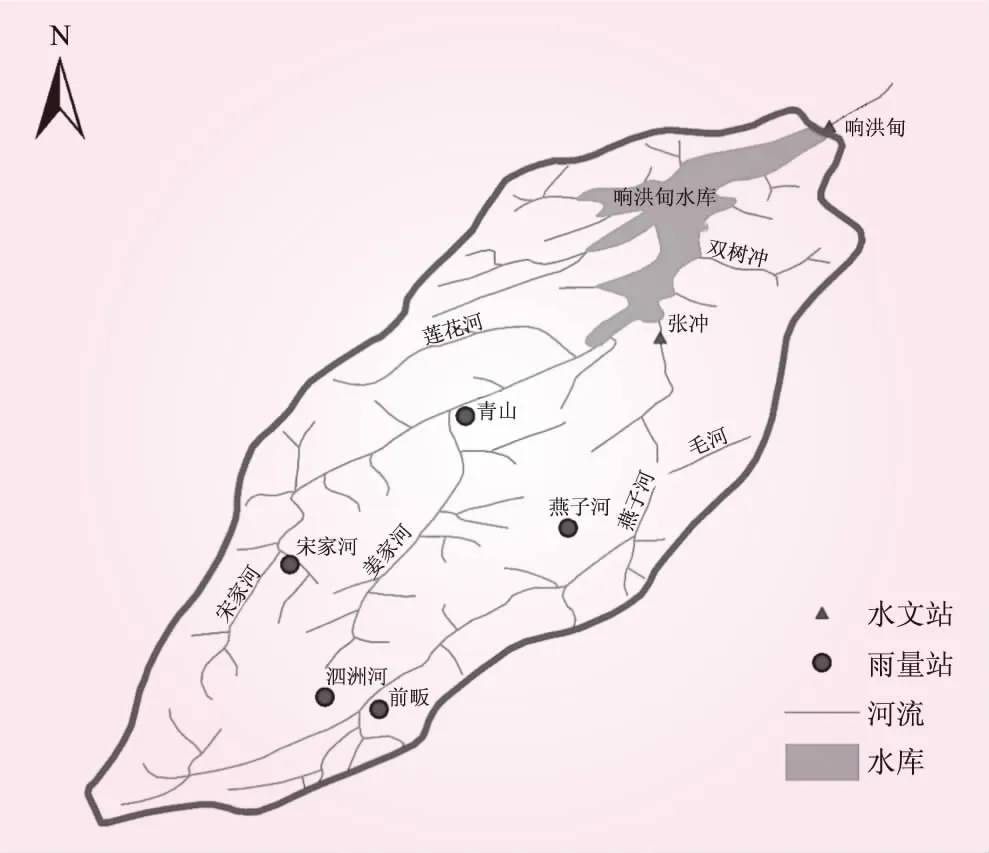
图2 响洪甸水库流域示意
本研究收集到响洪甸水库流域1998年至2006年间31场洪水资料,主要包括宋家河和响洪甸两站的雨量资料、响洪甸水库水位、出库流量以及水位库容曲线等资料。根据水量平衡原理,反推响洪甸水库入库洪水过程。考虑大中小不同量级的洪水过程,选择其中16场洪水进行模型训练,剩余15场洪水进行模型测试。计算时段长取1 h,以上时段雨量和入库流量为模型输入,预报下时段水库入库流量。模型结构为3个外部输入单元,4个隐含层单元和1个输出单元,隐含层向输入层的反馈延迟1个时段。
2.2 结果与讨论
利用训练集中16场洪水,对上述模型进行训练,模拟洪水过程。采用洪水总量误差、洪峰流量误差、峰现时刻差和确定性系数等指标评价各场洪水的模拟误差,训练结果见表1。
由表1可见,模型训练后对各场洪水的模拟精度总体较高,洪水总量和洪峰流量的相对误差绝对值平均为0.79%和4.17%,峰现时刻差平均为1.06小时,确定性系数平均值达到0.979。但各评价指标离散程度有所差别,洪峰流量相对误差离散程度要大于洪水总量相对误差离散程度,其变化范围为[-1.13%,10.6%],而洪水总量相对误差变化范围为[-0.38%,2.75%]。峰现时刻差变化范围为[-8,1],确定性系数的变化范围为[0.868,0.999]。
通过训练,确定了模型参数W和V,并利用该模型对预测集中15场洪水进行预测,预测结果见表2。
图4为部分洪水的预测过程。由图表可见,模型对预测集中15场洪水的预测精度也较高,洪水总量和洪峰流量的相对误差绝对值平均为1.22%和4.24%,两者均略高大于训练误差。但确定性系数平均值与模型训练时相同,且峰现时刻差小于模型训练时的峰现时刻差。相对于训练结果,除峰现时刻差之外其他3个指标的离散程度均大于模型训练时的离散程度。洪水总量相对误差变化范围为[-5.23%, 2.49%],洪峰流量相对误差变化范围为[-5.02%, 12.6%],确定性系数变化范围为[0.857, 1.000]。
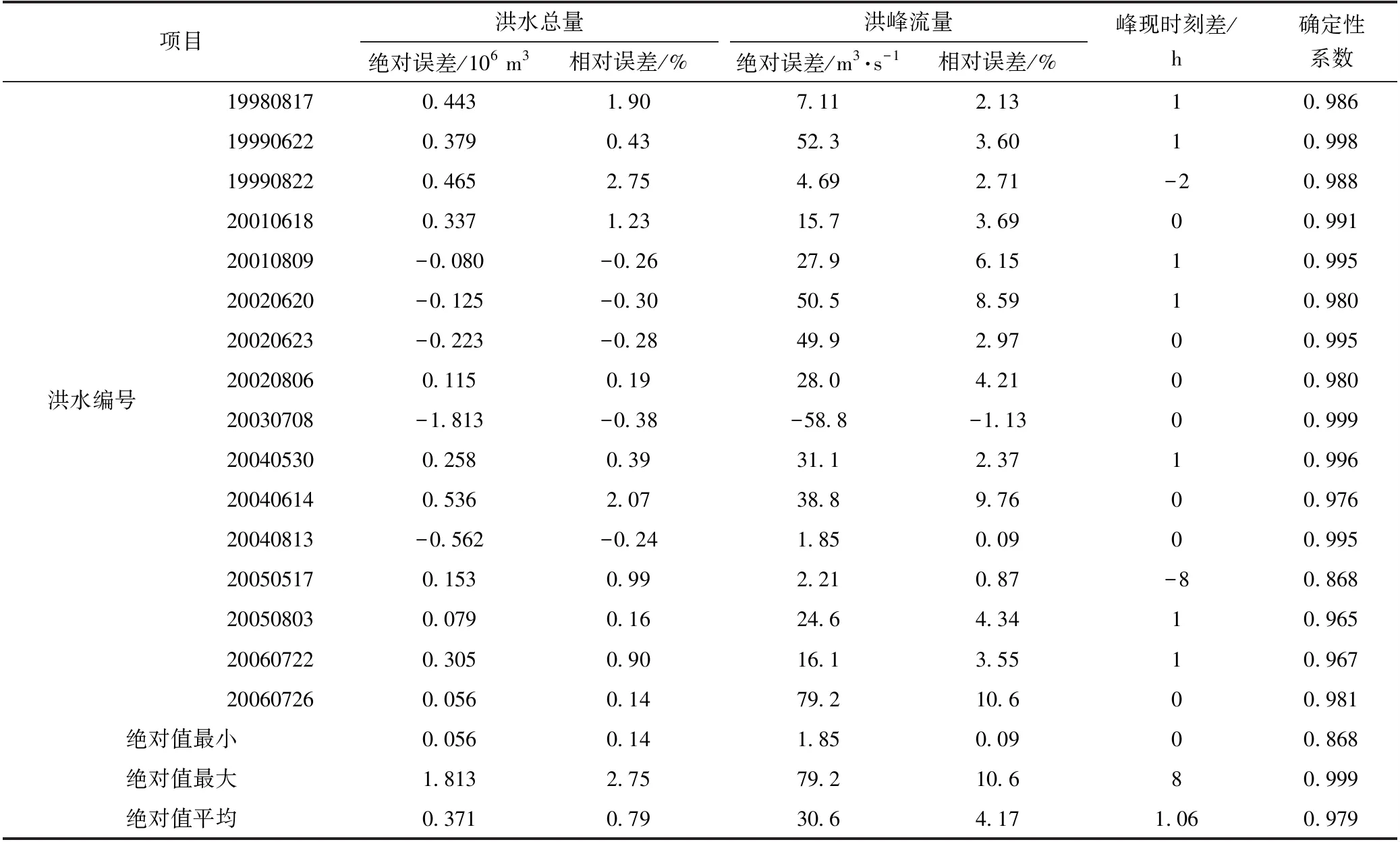
表1 训练集中16场洪水的模拟结果
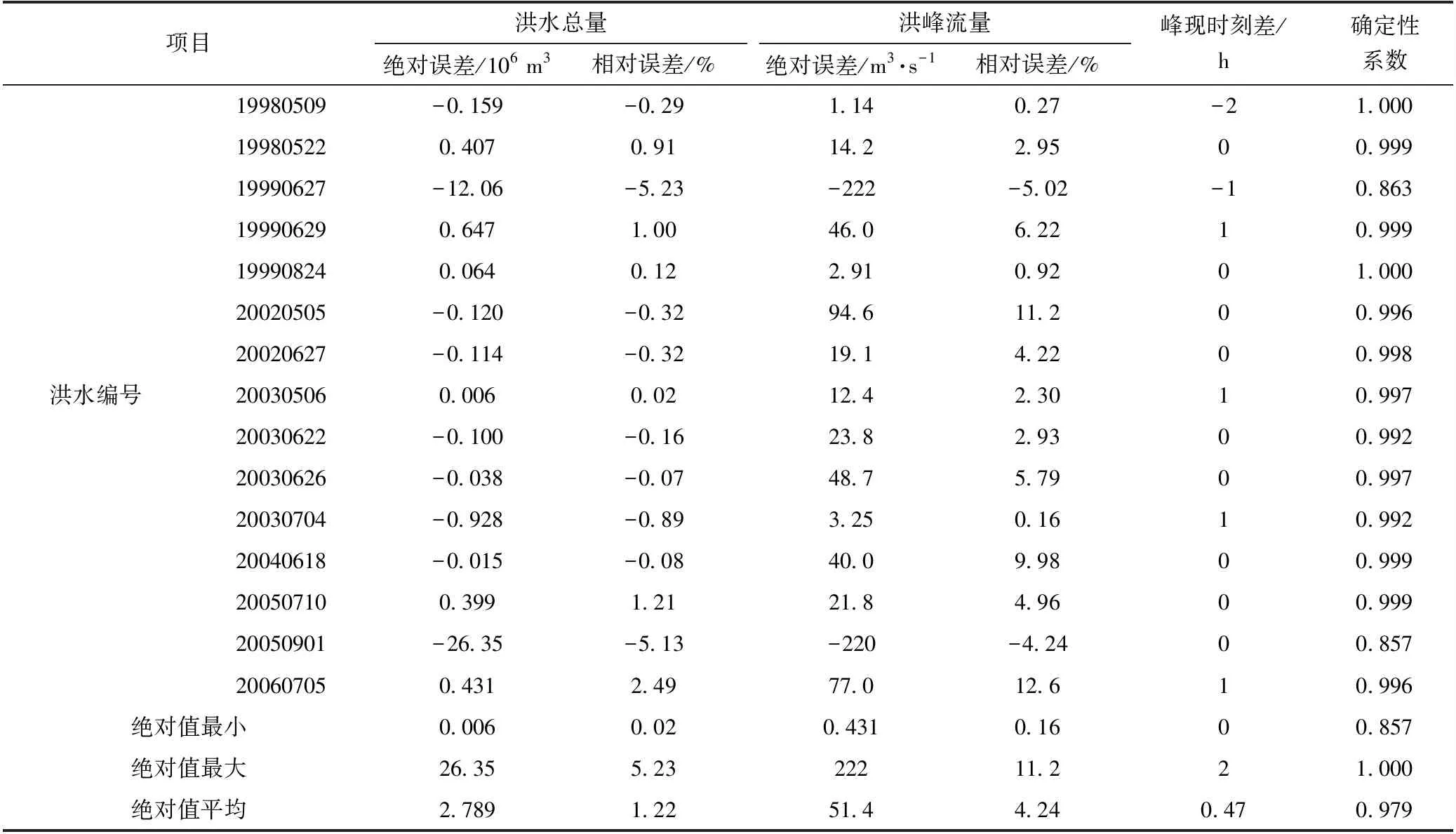
表2 测试集中15场洪水的预测结果
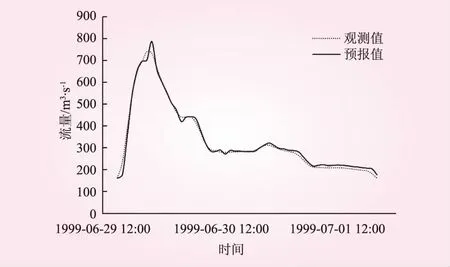
图3 19990629号洪水预报过程
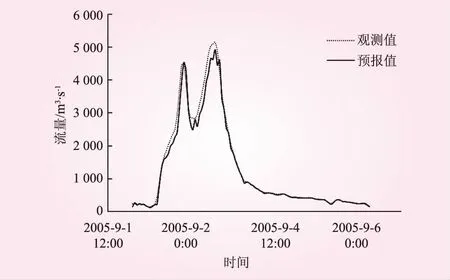
图4 20050901号洪水预报过程
3 结 论
通过上述实例研究,得到以下结论:
(1)利用动态神经网络构建洪水预报模型,模型输出不仅依赖于当前模型当前输入,而且还依赖于前期模型输入和模型状态,很好地反映了流域洪水动态变化特征。
(2)利用实时递归学习算法进行模型训练,随时间进程实时修正网络权重,使得该算法和动态网络模型能够很好地适应实时洪水预报的要求。
(3)基于Elman网络的响洪甸水库洪水预报模型能够得到较高的预报精度,洪水总量和洪峰流量的相对误差绝对值平均为1.22%和4.24%,确定性系数平均达到0.979。
然而,本研究中采用的预见期较短,需要在后续研究中进一步研究较长预见期的动态网络实时洪水预报模型,以更好地满足防洪决策要求。
