基于DEM的河宽模型在山区中小流域内的构建与应用
2019-07-25李致家童冰星
何 蒙,李致家,童冰星,谭 君
(河海大学水文水资源学院,江苏 南京 210098)
0 引 言
在构建中小河流分布式水文模型时通常依据遥感遥测数据或地形地貌资料将流域划分为若干个正交栅格,并将这些栅格分为河道栅格和坡地栅格。采用Muskingum-Cunge[1]方法进行河道汇流时,通过有限差分求解运动波方程来近似扩散波方程。这需要给出各河道栅格单元内的河道断面宽度;然而,由于有限的资金和人力资源,往往不可能测量流域内所有河道断面的宽度。因此,如何较为合理可靠地估算河道栅格单元内的河道断面宽度成为分布式水文模型汇流计算时的重点和难点问题[2-7]。
国内外的许多学者对此开展过广泛的研究[8-10],利用统计拟合法,在常规的河道水文数据的基础上,将河道宽度与断面常年的流量、输沙量等水文要素之间建立起经验性质的统计关系[11-15]。
统计拟合法原理简单,易于操作,但是经验性较强,难以取得一个普遍的通用公式,局限性较大。一般认为上游集水面积与河道宽度成正相关系,集水面积越大,河道越宽,即河道从上游至下游会因为集水面积的不断增大而逐渐加宽,然而这与实际并不相符,实际上中小河流下游局部河段的河道宽度也可能小于上游河宽[16-17]。因此在中小河流上需要一种符合客观实际,能够结合有限的资料简便可靠地估算河道断面宽度的新方法。
1 方法原理
1.1 影响河道宽度的因素选取
山区性中小流域河道流量普遍较小,地形地貌对河道形状的控制作用较大。因此,河道的宽度整体上具有从上游到下游逐渐增大的趋势;同时,在局部河道上受到地形地貌的影响,河道的宽度又会产生局部波动,有可能出现下游河宽比上游河宽小的情况[16-17]。因此,本文从整体性增大趋势和局部的上下波动两个方面考虑中小河流的河道宽度,综合分析各种因子的实际物理意义和提取的难易程度后,主要对河道两岸的坡度、集水面积与河道宽度之间的关系进行研究。
本文以陕西省大河坝流域作为研究示例,使用美国太空总署(NASA)和国防部国家测绘局(NIMA)提供的90 m分辨率DEM数据建立河宽模型。基于ArcGIS软件对DEM数据进行填洼,计算坡度、流向,进行汇流累积等一系列的地理分析处理[18-19],提取出大河坝流域的水系(见图1)。在Google Earth中取若干个样本断面,以米为单位测量出样本断面的宽度[20-21]。测量时并不限于水体部分的宽度,而是以两侧的稳定河岸为边界对经常性过水的河床进行测量(见图2),其测量的结果如图3所示。

图1 大河坝流域水系

图2 样本断面测量
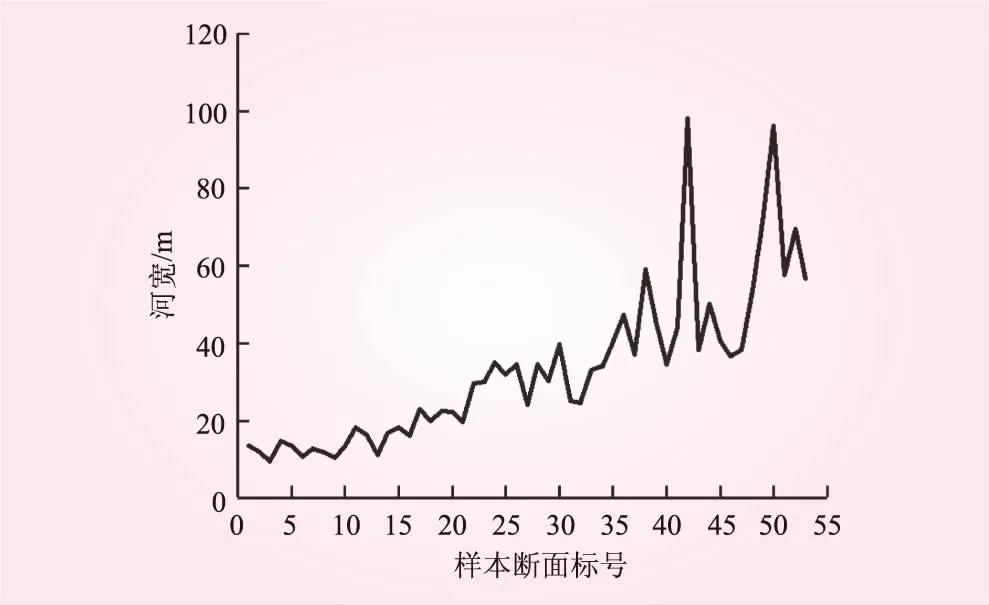
图3 样本断面处的河道宽度
1.2 影响河道宽度的趋势性因素
按照样本断面的上下游位置在横坐标上由左向右依次排列,将各个样本断面处的河道宽度与其对应的集水面积进行分析比较(见图4)。结合式(1),计算河道宽度与集水面积之间的斯皮尔曼等级相关系数(Charles Spearman,ρs)。该系数用来衡量两个数据序列的变化趋势的一致性,其值在-1和1之间变化。计算得到的河道宽度与集水面积两者之间的ρs为0.937,此时的n为52。这两个变量之间的相关性具有99%的置信度。因此,可以认为这两个变量的变化趋势较为一致。同时,蒋成伟、谢慧民、钟向宁等学者经过研究都认为河道宽度与上游集水面积之间有很强的相关性[2,17,22]。因此,本文将集水面积作为影响河道宽度变化的趋势性控制因素。即
(1)

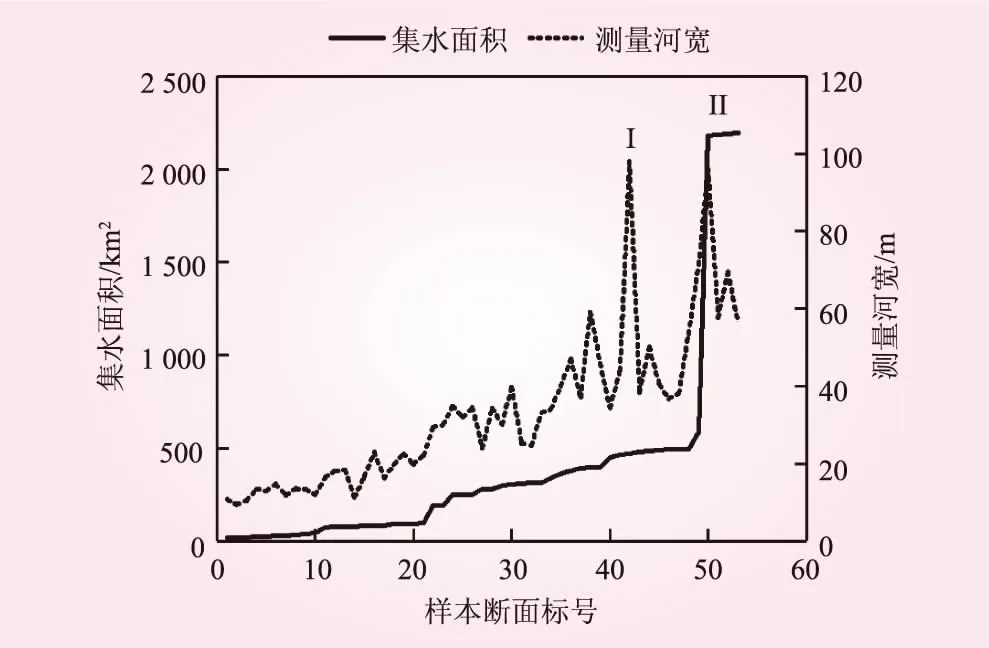
图4 样本段面处河道宽度与集水面积的关系(I、II处河宽大幅增大主要是受到建坝蓄水的影响)
1.3 影响河道宽度的局地性因素
河道两岸地形地貌特性的变化对山区中小河流局部河段的河道宽度影响较大。若河段附近植被茂盛,降雨充沛,土质疏松,沟谷开始发育的地质年代较早,则河谷受到的侵蚀作用较大,常常导致河道两岸的坡度较为平缓。平缓的河岸对于河道水流的约束作用较小,在水流作用下主河道易于摆动,使得河床较宽,在洪水时容易形成浅宽的过水断面;反之,若河道附近为坚硬的岩石,沟谷发育的时间较短,则两岸山坡一般较为陡峻,对于水流的约束作用较大,使得河道宽度较小,常会形成窄深的过水断面。因此,本文将反映地形地貌特征的坡度因子作为影响河道宽度变化的局地性控制因素。
基于DEM数据直接计算的坡度通常只能反映相邻河道栅格单元之间水面的起伏变化程度。一般而言,其值较小,接近于0度,不能够充分反映河道周围的地形地貌特征对于河道的影响。为将局部地形地貌对河道的影响进行量化,本文以河道栅格单元为中心,根据式(2)设置一定的搜索半径,提取出搜索半径内所有栅格单元的坡度值。通过计算这些坡度值的一阶原点矩来度量河段附近的地形地貌对于河道的约束作用的大小,并且按照这种计算方法得到每一个河道单元附近的坡度一阶原点矩(以下简称“坡度原点矩”)。即
(2)
式中,R为搜索半径;Bmax为最宽的断面宽度,可以根据流域资料或通过Google Earth来大致确定;D为所用的DEM分辨率。坡度原点矩
(3)
式中,n为搜索半径内所有栅格单元的个数;i为搜索半径内栅格单元的编号;Si为搜索半径内编号为i的栅格单元的坡度值。
1.4 河宽模型的构建
趋势性因素反映的是整体性变化趋势,一般与数据样本序列的上下界以及样本点在序列中所处的位置有关。用函数表达为
(4)
式中,fa为趋势性因素;MaxAi为最大集水面积,即流域面积;Ai为每一个河道栅格单元上的集水面积;T为该流域中形成河道的集水面积阈值,若栅格单元以上的集水面积大于该阈值则认为该栅格单元为河道,否则判定为坡地,不估算河道断面宽度。
局地性因素一般只与河道附近的地形地貌有关,本文提出的局地性因素具体的函数表达式
(5)
式中,fs为局地性因素;MaxMeri为最大的坡度原点距;Meri为每一个河道栅格单元的坡度原点距。
为反映趋势性因素和局地性因素对河道宽度的综合影响,将趋势性因素fa和局地性因素fs作乘积,并将该乘积称为河宽因子fte。河宽因子与河道断面宽度关系如图5所示。
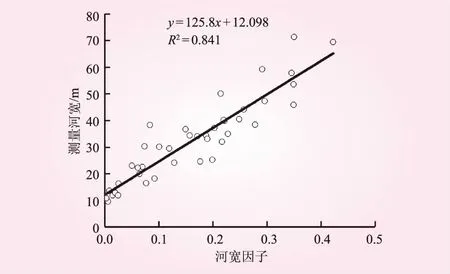
图5 河宽模型的参数拟合
采用一阶方程来拟合河宽因子与河道宽度之间的函数关系,得
B=δ×fte+β
(6)
式中,B为中每一个河道栅格单元的河宽;δ为河宽模型的比例系数;β为河宽模型的基础河宽,即河源附近的河道宽度,其值可以大致等于河源点处河道宽度的算术平均值。
2 算 例
选取陕西省秦岭北麓的陈河流域,以及属于湿润地区的浙江省昌化流域和於潜流域对该方法进行验证,基于90 m分辨率的DEM构建河宽模型,将不同流域的应用结果进行对比分析。同时,为研究DEM分辨率对于该方法的影响,在大河坝流域上基于美国太空总署(NASA)提供的30、1 000 m分辨率的DEM重新构建河宽模型,将不同分辨率下的应用结果进行对比分析。
2.1 流域简介
昌化流域和於潜流域位于浙江省西北部,昌化流域面积905 km2,於潜流域面积363 km2。这两个流域均属浙西山丘区,水系发达,急滩弯道处多有岩石和大块石,滩多流急,水位暴涨暴落。流域气候属于亚热带季风气候,多年平均年降雨量为1 638.2 mm。
陈河流域位于陕西省,流域面积2 249.7 km2。上游大部分为高中山区,峰谷相间,地形破碎,山坡多为凹凸坡,峪口,附近和沿河两岸有低山丘陵。属北温带大陆性季风气候,多年平均降水量700~900 mm。流域水系见图6。

图6 流域水系
2.2 计算结果
在Google Earth中测量图6中每一个流域河源点处的河宽,并分别计算其均值作为各个流域的基础河宽(β)(见表1)。同时结合各流域实地调查资料及影像资料,在每一个流域未明显受到水利工程影响的河段上均选取若干样本断面,量取出这些样本断面处的河道断面宽度作为实测资料。将70%的测量点用于率定的值,进而构建各个流域的河宽模型,同时将30%的样本断面用于验证河宽模型的效果(见表2)。

表1 各流域的 δ和 β的值

表2 各流域误差统计结果
各流域样本断面处估算得到的河道宽度与实测得到的河道宽度对比如图7~9所示。

图7 陈河测量河宽与估算河宽的比较

图8 昌化测量河宽与估算河宽的比较
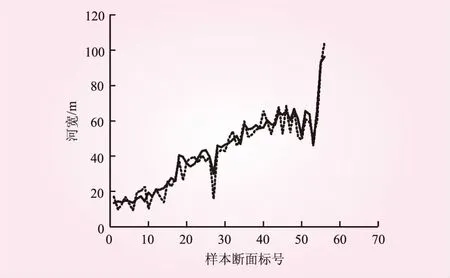
图9 於潜测量河宽与估算河宽的比较
通过表2可知,在湿润的昌化、於潜流域中,本方法估算得到的河道宽度误差约为15%~16%,而处于半湿润地区的陈河、大河坝流域,本方法估算得到的河道宽度误差约为17%~18%,略大于湿润地区的流域。通过实地勘察分析和卫星影像分析,可能是由于半湿润流域的年降雨量较少,且蒸发量较大,使得地区缺水量大。即使在夏季,河道中的水面只占整个河道很小的一部分,河道中常常出现大片的无水滩地。这种大片的河滩并不常年过水,只是在出现洪水时才会用于行洪,且每一次洪水中,河滩被淹没的面积不一。这使得在Google Earth中测量河道宽度时不易确定两岸边界,测量得到的河道宽度数据存在较大的误差(见表3、4)。
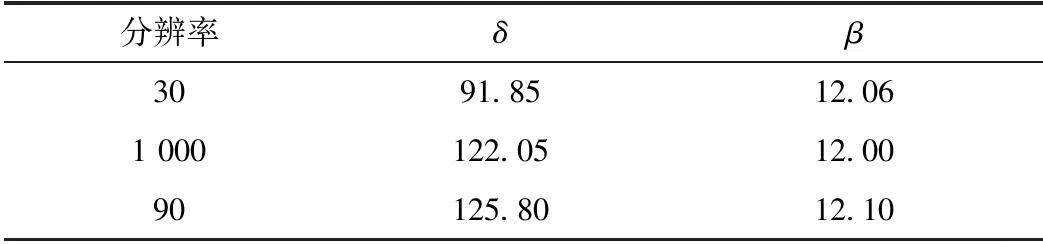
表3 大河坝不同DEM分辨率的 δ和 β的值 m

表4 大河坝流域不同DEM分辨率下误差统计结果
分析表4可得:在大河坝流域上,基于三种分辨率的DEM数据建立的河宽模型都能取得较好结果,且精度相差不大。这可能是本方法在确定模型的参数时,根据适线法的思想将样本断面的实测河宽与该断面对应的河宽因子进行拟合,率定出δ的值。通过调整δ的大小,使得样本断面处估算得到的河道断面宽度尽量接近测量得到的河道断面宽度,以确定合适的 ,进而构建各个流域的河宽模型。基于不同分辨率DEM数据的模型具有不同的 ,使模型能够适应不同的DEM分辨率;因此,DEM分辨率对本方法影响较小。
综合上述分析并结合流域的实际自然地理情况,在未明显受到水利工程影响的河段上,文中所提出的方法可以对中小河流的河道宽度做出较为准确、可靠的估算。使用此方法基于90 m分辨率的DEM对各流域中每一个河道栅格单元的河道宽度进行估算,其结果见图10~13。

图10 陈河河道栅格单元河宽估算结果
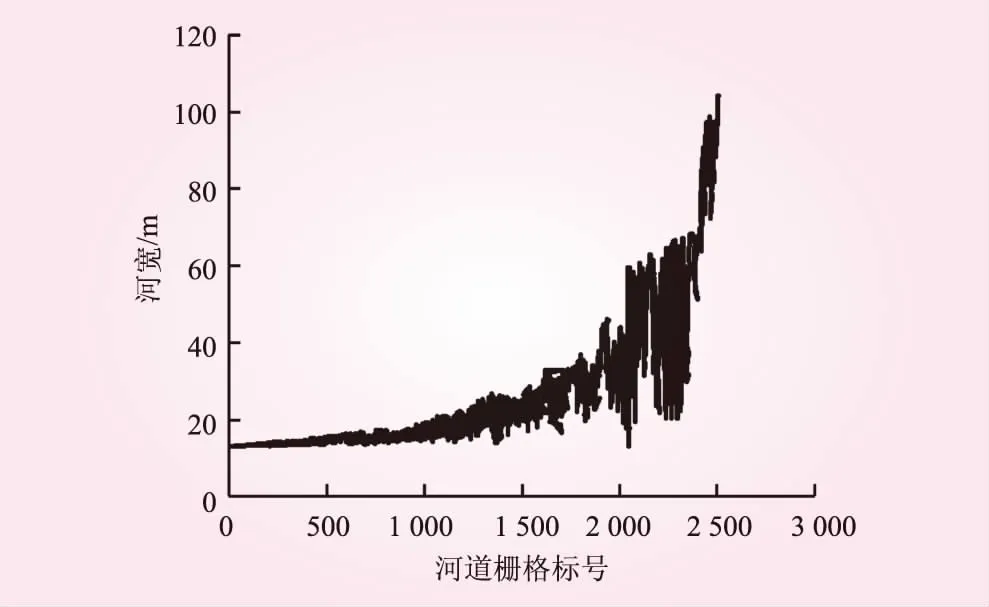
图11 昌化河道栅格单元河宽估算结果
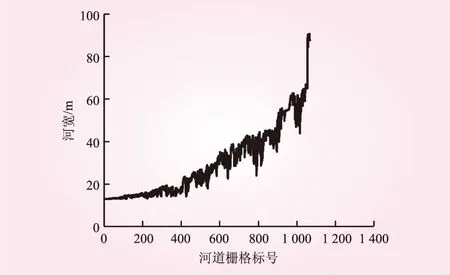
图12 於潜河道栅格单元河宽估算结果

图13 大河坝河道栅格单元河宽估算结果
3 结论与展望
本文提出的河宽模型在使用集水面积的基础上,引入河道栅格单元的坡度原点矩,量化了地形地貌对于局部河道宽度的影响,突出了局地性因素对于河道的控制作用,有效提高了山区中小流域河宽估算的精度。研究结果表明,在未明显受到水利工程影响的河段上,本文所提出方法能够较为准确得刻画出自然条件下河道宽度从上游到下游的变化特点。此外,本方法通过对趋势性因素和局地性因素的归一化处理,及河宽因子与测量河宽的拟合过程,有效的减小了DEM分辨率对本模型的影响,提高了模型的适用性。因此DEM分辨率对本方法计算结果影响较小。
但需要指出的是:由于水库大坝等大型水利工程以及一些特殊自然条件的影响,在局部河段上,本方法估算的河道断面宽度仍然存在较大的误差。此外,本方法适用于受地形影响较大的山区中小河流;对于大江大河,水面一般较宽,会形成连续带状的坡度接近于0的栅格,计算坡度原点矩时非河道栅格所占的比例很小,计算出的坡度原点矩并不能充分反映河道两岸对于河流的约束作用。因此,如何估算特殊局部河段的河道宽度以及如何改进大江大河的河道宽度估算方法将是下一步的研究方向与主要内容。
