《分数的意义》教学思考与实践
2019-07-25倪斌强
倪斌强
一、课前思考
《分数的意义》这一内容,经常作为公开课来展示,大部分教学是从把一个整体(如蛋糕、大饼等)平均分成若干份后,表示出其中的一份和几份,但笔者觉得仅从“等分除”这个方面来学习分数会使学生认识不全面,因为分数还有一个方面是“包含除”。我们应该从这两个方面来理解分数,不可偏废。
分数是怎样产生的?人教版教材给了我们一个很好的回答。分数有两种产生方式:一是在具体分实物的时候(如分蛋糕、苹果、饼干等),平均分成若干份后,表示出其中的一份或者几份。也就是用分数表示“整体中的部分有多大”,这就是平均分中的一种情况——等分除。二是先知道了结果,然后通过计算或者测量后才知道一共平均分成几份,再写出分数。如教材中几个古代的人用等距离打了结的绳子测量长方体石头的长时多出的那“一丢丢尾巴的长度”怎么记?其实可以用那多出来的“一丢丢尾巴的长度”去测量或计算,“一个单位长度”包含着几个“一丢丢尾巴的长度”,然后用分数表示,这就是平均分中的另一种情况——包含除。但遗憾的是教材到后面没有回应这个“一丢丢尾巴”如何处理,如何用分数表示。教学中教师也是对“等分除”宠爱有加,而对于“包含除”却视而不见。在分数的意义这节课中,对于意义的概括也只是“等分除”,没有“包含除”的一点影子。只倾向于部分和整体的关系,而两个量之间的比较是没有涉及的;只认识到真分数,也没涉及到假分数。笔者认为这样在学生脑中构建出来的分数是残缺不全的,不利于学生对分数意义的真正理解。所以,对于这节课笔者有了新的思考,进行了实践,并取得了较好的效果。
二、教学过程
【片断一】
1.对于分数你已经知道什么?
(学生交流各种表示方式)

生:因为都是把一个物体平均分成4份,取其中的1份。
【片断二】
师:从10个圆中任选几个看作一个整体,用阴影表示出你选择的这些圆的。(提供6组圆,有不同想法的可以在后面几组圆中表示出来)
(学生独自表示,反馈交流)
1.展示把4个圆看作一个整体的图并提问学生的想法。

2.展示把8个圆看作一个整体的图并让学生说说想法。
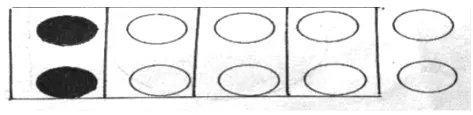
3.展示把10个圆看作一个整体的图并让学生说说想法。
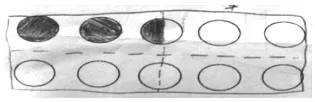
生:把一个整体平均分成4份,空白部分占其中的3份,也就是这个整体的。
师:数学上把一个整体叫做单位“1”,那什么是分数?
生:分数指把单位“1”平均分成若干份,取其中的1份或几份。
【设计意图:选取用10个圆作为研究分数的素材,主要有以下几方面好处:一是体现学习的差异性,学习稍弱的学生可以圈出4的倍数,而程度好的学生可以圈出不是4的倍数,当部分学生能够把完整的圆破开,把2个、6个、10个,甚至5个等看作一个整体表示出后,是真正理解了分数的本质属性。二是集中火力构建,学习更开放、更有挑战性,学生的思维不局限于教材中呈现的都是倍数关系的,拓展了学生的思维。三是在学生多元化表征的过程中给课堂教学提供了更丰富的观察比较素材,在“同中求异”(都是,怎么一会儿表示一个圆,一会儿两个圆,一会儿又是两个半呢?)和“异中求同”(总个数不一样,为什么都可以用表示?)的比较过程中,进一步认识了分数的本质属性与总个数无关,只与平均分的份数及取的份数有关。】
【片断三】
下图中,你能找到哪些分数?先分一分,再写一写。

师:说一说你找到了哪些分数,分别表示什么意思?

师:单位“1”一样,涂色部分的个数相同,为何表示的分数不相同?
师:把单位“1”平均分成若干份,其中1份就是分数单位。分别说一说图中各个分数的分数单位以及有几个分数单位组成。
师:分数单位是由什么决定的?
生:是由平均分的总份数决定的,也就是分母决定的。
师:说得好,当平均分的总份数决定了以后(板书:分),也就是知道了分数单位,再数一数有几个这样的分数单位(板书:数),这就是分数。所以分数分数,就是先“分”后“数”的数。
【设计意图:12个三角形中有6个涂上阴影,用分数表示出阴影部分,学生表示出的分数很丰富,进一步巩固对分数的理解。更为重要的是加大分数单位的教学力度,学生在直观图中分别说一说“各个分数的分数单位以及有几个分数单位组成”,使学生很容易理解分数就是分数单位的累加,是先“平均分”成若干份得到分数单位以后,再从中数一数有几个这样的分数单位的数。】
【片断四:比眼力】
1.出示一条长方形的纸,假设这是单位“1”,接着出示另一张纸条是单位“1”的一半,让学生估一估。
生:比划一下。
师:正确的只有一个,那到底是谁呢?怎么办?
5.出示与单位“1”一样长的纸条,用分数怎么表示?
师:为什么这些分数都可以?
生:因为我们可以把单位“1”平均分成2份、3份、4份等任意份数。
师:如果平均分成a份呢?
生:1倍多。
师:用分数怎么表示?
师:你是怎么想的?
师:大家同意吗?怎么验证?
生:量一量。
师:怎么量?
师:真是太厉害了,这也是分数中的一种,叫做假分数,这个分数与前面学的分数有什么不同?
生:分子比分母大。
师:那前面学的分子比分母小的分数叫什么分数呢?
生:真分数。
【设计意图:通过“比眼力”的活动,一方面进一步使学生理解分数是分数单位的累加;另一方面让学生估计长方形纸条的长度,学生在估测的过程中,发现要验证估计的是否准确,需要借助分数单位来测量,有几个这样的分数单位就是几分之几。对于假分数,通过测量有5个,学生也能够很自然的建构,就是。这样对于分数的认识是完整的。因为不仅有前面的“等分除”的认识,而且还有“包含除”的情况,这其实是对教材一开始呈现的几个古代的人用等距离打了结的绳子测量长方体石头的长时“多出的那一丢丢尾巴的长度怎么记?”的一种回应。需要用多出的绳子长度去比划、测量(或计算)打结处(单位1)长度,设法构造出一个分数单位,发现有几个这样的分数单位,最终把它的大小用几分之几表示出来,也就产生了分数。还有让学生认识到分数除了部分和整体的关系外,还有两个量之间比较的结果(如两根纸条的比较)。】
