改进的KCF算法在车辆跟踪中的应用

(西安理工大学 自动化与信息工程学院，西安 710000)

0 引言

随着我国汽车行业的不断发展，国民生活水平的不断的提高，汽车已成为人们日常的代步工具。随之而来的是交通事故的频发，以及带来的巨大的人身伤害和经济损失，导致交通事故已经成为全球性安全问题之一。因此，智能交通系统(intelligent transportation system，ITS) 作为解决方案被提出并且得到了快速发展。基于视频的车辆跟踪技术已经逐渐成为智能交通系统 ITS[1]以及智能交通管理技术的关键技术之一。近年来，研究人员针对车辆跟踪问题提出了很多优秀的跟踪方法。Wang[2]等人通过引入多特征融合方法，同时利用混合高斯模型体现运动目标的颜色分布，然后 加入空间信息，将运动目标的多种外表所能观察到的特征进行了相应的组合，最终获得更为精确的目标分析模型。张彤[3]等人提出了一种改进的Mean-Shift自适应跟踪算法，通过运动目标的历史信息预测下一帧目标的位置来优化 Mean-Shift跟踪算法，该算法具有良好的实时性和鲁棒性。Chang[4]等人提出了一种基于车辆部分侧面的实时车辆跟踪方法。该方法采用AdaBoost算法训练不同的弱分类器组成强分类器，通过Kalman滤波预测车辆的每一部分在图像中的位置，重新定位跟踪窗口。该方法在车辆存在部分遮挡，光照强弱变化的条件下，能够有效提高跟踪的效率和准确性。Uchimura[5]等人针对遮挡情况下的车辆跟踪，提出一种基于分块的车辆跟踪算法。该算法将目标车辆以可重叠的方式划分为若干大小一致的子块，在分块的基础上实现车辆跟踪。建立了马尔可夫随机场描述子块之间的关系，利用欧氏距离定义块的邻域，并基于块的直方图构建能量函数，最后利用模拟退火法对能量函数进行优化，以对遮挡区域进行分割。单玉刚[6]等人针对多目标粘连的问题,提出了区域运动相似性分割方法和相似度关联矩阵的解决方案。首先采用背景差法进行运动检测，经过形态学滤波和合并处理提取当前帧中运动目标区域，然后对检测出含有粘连运动目标区域分别采用基于区域运动一致性分割算法进行车辆粘连分割，取得较好分割效果，具有很好的鲁棒性和适用性。Gao[7]等人还提出了一种基于YcbCr颜色空间的阴影分割算法并采用自动粒子滤波算法对车辆进行跟踪，跟踪效果具有很强的鲁棒性。

目前常用的车辆跟踪算法包括基于车辆的轮廓、特征、模型、区域的跟踪算法[8-12]。 但是在复杂道路场景下，相似车辆之间的干扰、严重遮挡、旋转及尺度变换一直是车辆跟踪的难点。因此，基于视频的车辆跟踪算法仍需要改进。

1 KCF跟踪器

KCF[13]跟踪器是以岭回归为核心，在线训练的一个判别式分类器。该跟踪器的跟踪效果与跟踪速度表现都十分亮眼，之所以有这么好的效果，得益于作者使用循环样本矩阵作为分类器的训练样本。然后根据循环矩阵可以离散傅里叶对角化的特性提高了跟踪器的性能。

1.1 样本生成

KCF跟踪器的训练样本都是在线产生的，初始化跟踪目标区域为正样本，然后根据循环矩阵理论分别左乘，右乘置换矩阵进行图像的循环移位得到负样本集合。记目标样本为向量x=[x1,x2,…,xn-1,xn],x循环移位可得循环矩阵X，即:

(1)

根据循环矩阵的性质可将其离散傅里叶变换(DFT)矩阵对角化为：

(2)

其中:F是用来计算DFT的常量矩阵；H表示矩阵共轭转置； “^”表示一个向量的傅里叶变换，下文将不在说明。

1.2 分类器的训练

分类器的训练就是在损失函数最小的情况下获的岭回归的最优解，并且循环矩阵的性质可以简化岭回归的解。线性岭回归目标函数为：

(3)

其中:λ是控制过度拟合的正则化参数，f为基样本的线性组合，即：

f(xi)=wTxi

(4)

岭回归的闭式解为：

w=(XHX+λI)-1XHy

(5)

其中:I为单位矩阵，也是循环矩阵，由式(2)的性质可得：

(6)

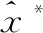
在非线性回归的情况下引入了核函数，把低维空间的计算映射到高维核空间。假设样本的非线性映射函数为φ(x)，则：

f(z)=wTφ(z)

(7)

根据Representer定理得岭回归的最优解：

w=∑iαiφ(xi)

(8)

将(7)和(8)代入(3)式可得核空间的岭回归的解为：

α=(K+λI)-1y

(9)

其中:K=C(Kxx)=φ(X)φ(X)T为所有样本之间的核相关矩阵；α为系数αi的向量。由K是循环矩阵,可得(8)式频域下的解为：

(10)

其中:kxx是核相关矩阵K的第一行。

1.3 快速检测

待检测样本集，是由上一帧的预测区域和由其循环移位得到的样本集合zj=Pjz，P为置换矩阵。

对输入图像块z,KCF算法中的分类器响应为：

f(zj)=αTφ(X)φ(zj)

(11)

由分类器输出最大值的样本区域作为新目标区域,由zj判断目标移动的位置。

定义Kz是候选图像块和训练样本之间的的核矩阵，即：

Kz=φ(X)φ(z)T

(12)

由于Kz是循环矩阵，由(2)式的性质得到各个候选图像块在频域的响应为:

(13)

对式(13)做离散傅里叶逆运算，即可获得待检测样本的响应矩阵。采用线性内插法更新模型参数,即:

(14)

(15)

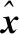
2 多尺度改进

KCF算法理论上属于一种密度集抽样检测，利用循环矩阵的性质在傅氏空间中使用离散傅里叶矩阵进行对角化,将复杂的卷积运算转化为简单的频域相乘,优化了算法在整个跟踪过程的性能。但是KCF算法依赖循环矩阵，当车辆发生尺度变化时，初始化的矩阵不能根据实际情况自适应地改变大小。这会导致分类模型的偏移、特征丢失，最终导致跟踪车辆漂移。所以，本文提出引入一个在线学习且独立于位置滤波器的快速分类尺度空间跟踪器，实现快速地尺度估算。

2.1 特征金字塔

在KCF算法已经估算出车辆位置的情况下，在该位置提取训练样本的S层主成分分析(PCA)-HOG特征金字塔。假设当前目标帧大小为P×R，尺度大小为S，提取目标大小为αnP×αnR的窗口标记为Jn。其中α表示一个尺度因子，n的取值范围如下：

(16)

2.2 尺度降维

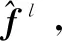
(17)

其中:λs为正则化参数。

有这么一个单词，看上去跟我意思相反，但是如果把我们放在一起，却是个绝佳搭配。你能帮我找到这个词吗？把它填到横线上吧。我们放在一起又是什么意思呢？选一选，把对应的中文写在方框里。

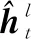
(18)

(19)

其中:l∈{1,…,d}表示特征维度。

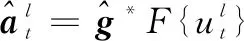
(20)

(21)

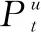
3 遮挡处理机制

核相关滤波算法在目标跟踪中,速度和准确度方面具有明显的优势。但在跟踪过程中并不涉及运动目标的状态信息，当运动车辆发生严重遮挡时，就会破坏分类模型，最终导致跟踪失败。因此，本文提出融合Kalman滤波器的跟踪机制，当目标车俩发生严重遮挡时，由kalman滤波器预测本帧图像中的目标车辆位置，再由核相关滤波器检测预测坐标周围的窗口，利用检测结果校准kalman滤波器。最终得到本帧图像中目标车辆的位置。

3.1 kalman滤波算法

kalman滤波算法的核心思想：以最小均方误差为最佳估计准则，根据系统的状态空间向量模型，利用前一时刻的估计值和当前时刻的观测值，从而预测出当前时刻目标可能出现的位置。

kalman滤波分为两部分：一个是状态方程、另一个是观测方程分别为：

xk=Akxk-1

(22)

(23)

其中:vk、Hk、zk表示k时刻测量噪声、测量矩阵、测量矢量；xk-1表示k-1时刻的状态矢量。则状态转移矩阵A、初始误差估计P0、观测矩阵H分别为:

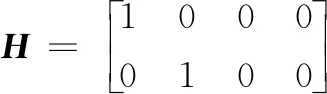
(24)

式中,Δt=tk-tk-1。

系统预测过程：

(25)

(26)

(27)

式中,Pk表示预测误差估计；Kk表示增益系数矩阵。

系统状态校准过程：

(28)

Pk=(1-KkHk)Pk

(29)

式中,zk表示k时刻由核相关滤波器检测的车辆位置中心点坐标。

3.2 遮挡处理

采用文献[16]的遮挡判别算法：

1)获取核相关滤波器最大响应值max和该最大响应值目标车辆的位置坐标pos；

2)获取pos周围满足大于λ1·max的所有的位置posi；

3)获取所有posi点到pos的欧式距离responsei；

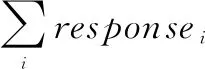
其中:λ1为遮挡阈值，λ2为面积因子；height、width分别为检测样本的高度和宽度。

如果目标车辆未受到遮挡，则继续使用核相关跟踪算法进行目标车辆的跟踪。如果目标车辆被局部遮挡，则核相关滤波算法输出结果将不在可信。则使用上一帧图像中目标车辆的状态信息来初始化卡尔曼滤波器的状态向量，xk= [xk,yk,xk′,yk′]T，其中(xk,yk)为目标车辆位置的中心坐标，(xk′,yk′)为目标车辆位置中心坐标的变化速度。采用卡尔曼滤波器的预测方程预测目标车辆在本帧图像中的位置。当目标车辆被严重遮挡时，则不能利用核相关滤波器输出结果校准卡尔曼滤波器预测结果。所以，设Δd表示核相关滤波器的检测坐标与卡尔曼波器的预测坐标的欧式距离。正常情况下，Δd比较小，设参数δ，当Δd<δ时，正常校准。当Δd>δ时，停止卡尔曼滤波器预测结果校准，直接根据卡尔曼滤波器预测坐标进行跟踪。

4 自适应模板更新

为了提高跟踪算法在复杂情况下的鲁棒性,相关滤波器每帧都会更新目标模板，以及时适应目标表观特征的变化。但是，目标模板的更新过程只基于当前帧，且学习率参数不能自适应地变化。当目标车辆发生遮挡时，模板将丢失目标车辆的特征，导致跟踪失败。所以，当目标车辆被遮挡时，希望适当降低学习率可以一定程度上减少更新误差。因此，当目标车辆被遮挡时，提出一种自适应更新学习率参数的方法。

(30)

其中:μ为调节系数。新的学习率参数为：

(31)

当目标车辆被遮挡时，使用新的学习率参数进行模板更新。新的学习率η′与遮挡程度成反比，当目标车辆被完全遮挡时，学习率η′趋于0，则不更新模板。相比于传统模板更新方式，当目标车辆被遮挡时，可以自适应地调节学习率参数，提高了模板的自适应更新能力。

5 实验参数及结果分析

实验的硬件平台是A8-4500 M，主频1.9 GHz，4 G内存计算机，软件采用VS 2013与OpenCV 3.1.0编程环境。实验中传统KCF算法的参数保持不变。学习因子η为0.02，高斯核标准差σ为0.5，正则化参数λ为0.000 1。本文参数设置如下：一维尺度相关滤波器正则化参数λs为0.01，学习因子η为0.025。遮挡阈值λ1为0.8，面积因子λ2为0.3，调节系数μ为0.85。本文选取两种不同情况下的道路车辆监控视频进行实验。视频1为目标车辆有尺度变化，视频2为目标车辆有遮挡和旋转。

5.1 尺度自适应对比试验

利用视频1进行尺度自适应对比试验，试验结果部分截图如图1所示。图中上，下两行分别表示改进前跟踪算法和改进后跟踪算法的试验结果。从图中可以清楚地看到视频中的汽车由远及近时，汽车的尺寸逐渐变大，改进后算法的跟踪窗口可以精确地随着目标车辆的尺寸变化而变化。

图1 尺度自适应试验结果对比

5.2 遮挡对比试验

利用视频2进行遮挡对比试验，试验结果如图2所示。图中上，下两行分别表示改进前跟踪算法和改进后跟踪算法的实验结果。从图中可以清楚地看到目标车辆在图2(b)中被其他车辆严重遮挡之后，改进前跟踪算法失去了目标车辆，不能继续进行跟踪；改进后跟踪算法借助遮挡处理机制及模板自适应更新在受到严重遮挡，部分遮挡之后仍然可以跟踪目标车辆，跟踪效果良好。此外改进后算法的跟踪速度可以达到60.5帧/s，虽然遮挡情况下会影响跟踪的速度但依然大于制式24帧/s，可以满足实时性的要求。

图2 遮挡试验结果对比

5.3 跟踪性能对比

图3 数据集Car1试验结果对比

图4(a)为改进前算法的跟踪误差曲线，图4(b)为改进后算法的跟踪误差曲线。车辆在第190帧(图3(a))驶入阴影区域之前两种算法的跟踪效果都很好，但是在车辆驶入阴影区域之后改进前算法的跟踪误差明显增大，并且没有进行修正；改进后算法能够一直保持良好的跟踪效果。

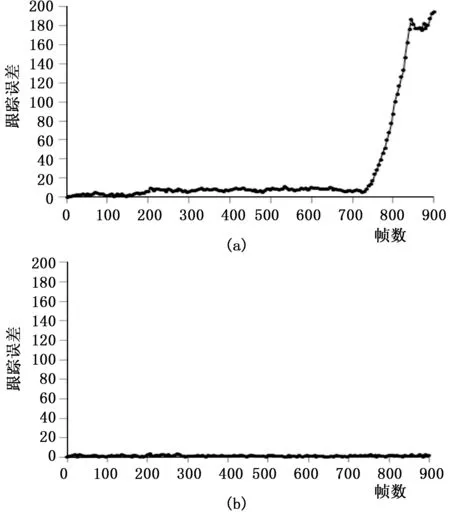
图4 跟踪误差对比

6 结束语

鉴于核相关滤波算法的时效性,本文对KCF算法进行改进,使之应用到复杂道路场景下的车辆跟踪。(1) 采用快速分类尺度空间跟踪器(fDSST)的尺度估计方法，进行尺度降维，相比于文献[14]的尺度估计方法速度提高了一倍。(2) 增加遮挡处理机制，通过遮挡判断，融合kalman滤波器进行预测跟踪。(3) 在目标被遮挡情况下，自适应调节学习率参数。实验表明本文方法具有较好的跟踪效果,并且可以保证跟踪的稳定性与及时性。但跟踪速度相比于传统KCF有所降低，下一步的计划是在不影响跟踪效果的同时，提高跟踪速度。