一种改进的决策树ID3 算法的应用

迟殿委

（山东外事翻译职业学院，威海264504）

1 决策树ID3算法简介

决策树[1]分类算法是数据挖掘领域很重要的一种算法，1986 年由Quinlan 提出的ID3[2]算法是一个很有影响力的决策树分类算法，Quinlan 和其他专家描述了决策树ID3 算法思想和理论，而且针对决策树展开了深入研究[3-10]。该算法采用分治方法，对一个训练集进行不断学习最终生成一棵决策树。其核心思想如下：

ID3 算法是计算每个属性的信息增益值，比较找出信息增益值最大的那个特征属性作为决策树的分类节点，根据该属性的不同取值进行分枝，然后对每个分枝的训练子集用同样的方法递归找到分枝节点和建立分枝，直到子集的所有实例属于同一类别[11]。

2 决策树ID3算法的改进

2.1 ID3算法存在的缺点

（1）特征取值较多的属性算出的信息增益一般会比较大，但这不一定合理。

（2）求信息增益的公式计算量较大，会限制构建决策树的速度。

（3）如果训练样本集合过大，由于ID3 算法不采取剪枝策略，可能导致过拟合，影响决策树的创建速度。

2.2 三个方面的改进

（1）为了让选取的特征属性更为合理，在建树之前可以根据业务领域专家给出每个属性对于分类的权重，引入属性重要度[12]。这样就会对属性的信息增益产生影响，从而让选取的分类属性更加合理。

参照领域专家的经验或知识为第i 个属性设置重要度Si，则新的信息增益公式为：

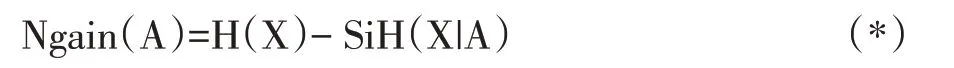
（2）ID3 算法中包括信息论[13]中的信息熵和信息增益，计算属性的增益值公式gain（A）计算量太大，可以进行简化[14]，从而提高算法效率。

为了简化分类场景，我们假设训练样本集合D 中包括2 种类别，分别是类别M 和类别N，假设类别M中样本个数为p，类别N 中样本个数为n，属性A 可以取到的值有a1,a2,a3,…,at,当A=ai 时，该取值对应分枝下样本共有ni+pi 个，其中有ni 个是类别N，pi 个是类别M。能够得出训练样本D 的熵对应如下算式：

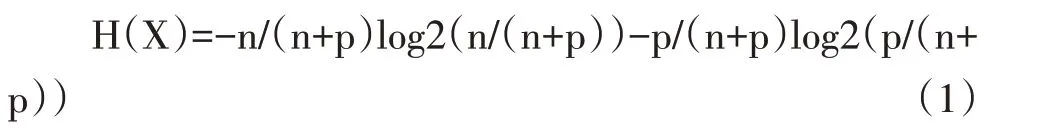
如果选择属性A，计算A=aj 结点Xj 的信息熵：

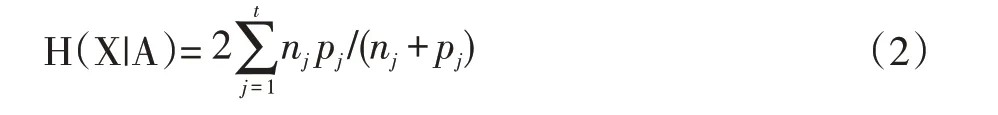
假设Yj 为A=aj 时的样本实例集合，决策树对以特征属性A 进行划分的不确定程度就等于训练样本对A 的条件熵：

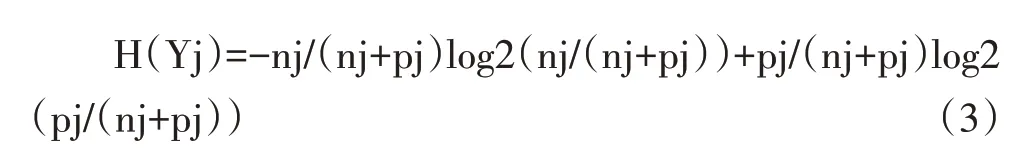
把（1-3）代入式子（*）求得增益值公式：gain（A）=H（X）-SiH（X|A）

因为无论选取什么特征属性，H（X）的值是不变的，所以只需要考虑SiH（X|A）的取值即可。

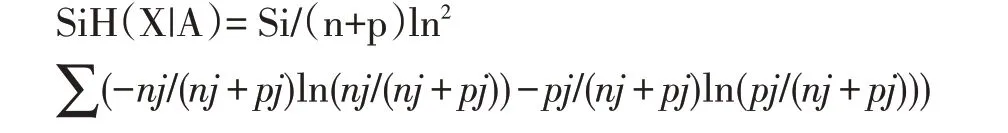
而1/（n+p）ln2 的值是确定的，所以公式进一步简化：

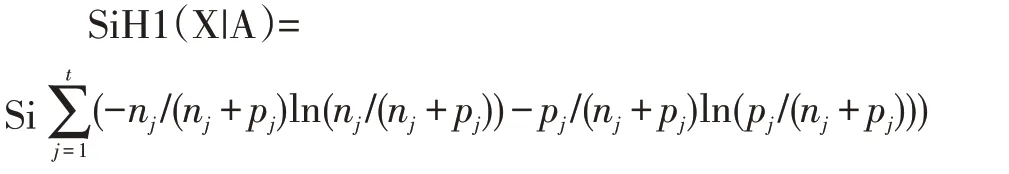
我们知道，ln（1+x）在x 趋近于0 的时候约等于x，而nj/（nj+pj），pj/（nj+pj）远小于1，所以公式最终化简为：

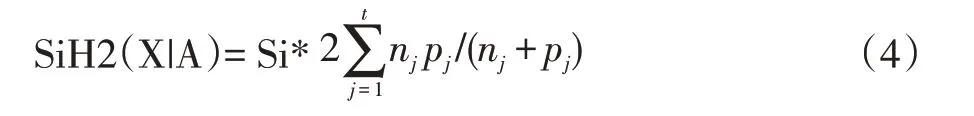
根据公式（*）可知，公式（4）取得最小值的特征属性作为最终选取的特征属性。

公式（4）的运算量只涉及到简单的加减乘除运算，相比于原来信息增益公式简化了很多，建树速度也会相应提高。

（3）为了防止决策树的完全生长，我们设置一个剪枝阈值，在建树过程中，如果某个特征属性的属性值对应的子集中，不同分类的比例超过设定的阈值，就停止决策树的生长，有效地防止过拟合。

2.3 改进后算法步骤

步骤1 加载读入训练样本实例集合；

步骤2 定义一个剪枝阈值value；

步骤3 开始递归构建决策树；

步骤4 根据公式（4）求出每个属性的增益值，选择取得最小值的属性；

步骤5 检验是否所有属性都已经选取完毕，如果选完就结束算法，否则需要继续计算每个属性值对应的子集中，每个类别的比值与剪枝阈值进行比较，如果大于该阈值就结束，否则跳转到步骤3 继续进行。

2.4 实例说明

表1 是大学生从事足球运动的训练样本集合，是否适合从事足球运动跟四个特征属性有关，分别是耐力、平衡性、力量、冲刺跑。这里根据体育专家的经验设置这四个特征属性对分类影响的权重值分别是：0.25,0.27,0.3,0.32。类别Y 表示适合从事足球运动，这里设定剪枝阈值value=0.8。

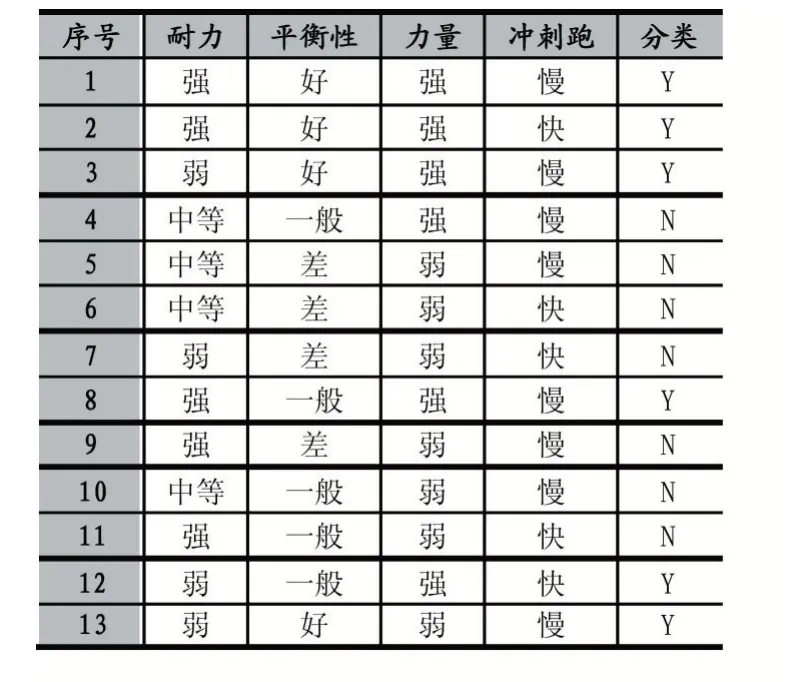
表1 一个足球训练实例集合

根据公式（4）计算每一个属性的增益值，得到表2。

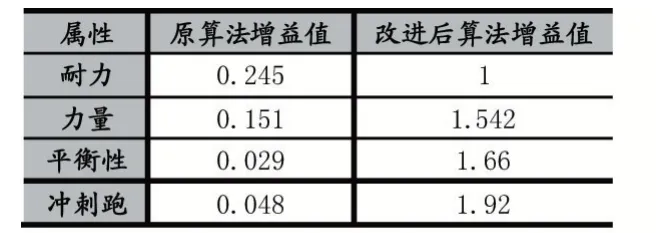
表2 算法改进前后增益值比较

分别使用原ID3 算法和改进后的ID3 算法步骤进行决策树的构造，结果得出的是同一棵，如图1。

图1 ID3算法决策树和改进后算法决策树

2.5 分析说明

（1）该实例引入了体育训练领域专家给出的特征属性的重要度，从最后产生的决策树可以看出，决策树分类结构合理，没有异常情况，有效防止了特征属性取值较多的属性一定首先被选中的问题。

（2）在表2 中看出，原公式gain（A）得到的身高属性的增益值为0.245，是所有属性中最高的，所以在决策树中为根结点。改进后的公式（4）得到该属性增益值为1，是所有属性中最小的，也应该被选为根结点，这说明简化前后选择的分类属性是一致的。其余分支结点的选择也有类似的结论。

（3）通常来说，设置的剪枝阈值越小，决策树的创建速度越快，但是分类的准确率可能降低。这里设置阈值为0.8，大量实践证明，这是一个合理的数值，可以保证一定的准确率，也能提高建树效率，这个剪枝阈值的设置尤其适合很大的训练样本集合。

3 结语

本文对决策树经典的ID3 算法从三个方面进行了改进：引入了特征属性的权重，设置了建树的剪枝阈值，简化了信息增益的计算公式。最终生成的决策树结构合理，建树速度明显提高，尤其适合训练样本数据集很大的情况。