人口预测问题的时间序列模型探究
2019-07-24王颖俐
王颖俐
(长治学院 数学系,山西 长治 046011)
数学家耶尔最早提出时间序列分析方法与自回归模型,此后不断发展完善。时间序列分析方法主要应用于预测,例如房价预测、碳排放预测、人口预测等等。
人口数量与地区及国家经济发展关系密切。因此人口的研究、预测与控制关乎国计民生。最早提出人口预测模型的人是英国人口学家马尔萨斯。随后,人们又提出logistic模型和随机性模型。文章选取1980-2017年的全国人口数据,采用时间序列分析方法建立模型进行分析及预测。具体数据见表1。
1 ARIMA模型介绍
ARIMA模型(自回归移动平均模型)是时间序列分析中使用范围较广的模型,其结构如下:

ARIMA模型建模的基本思想就是将差分运算与ARMA模型进行组合。首先将非平稳时间序列进行一定阶数的差分后转化为平稳时间序列,进而对差分后的序列拟合ARMA模型。它遵循如下操作流程(见图1)。

表1 我国1980-2017年年末人口数

图1 建模流程图
2 模型构建及分析
2.1 序列平稳性的判别
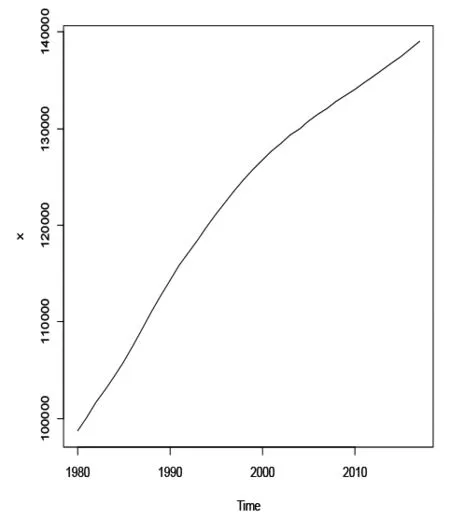
图2 时序图
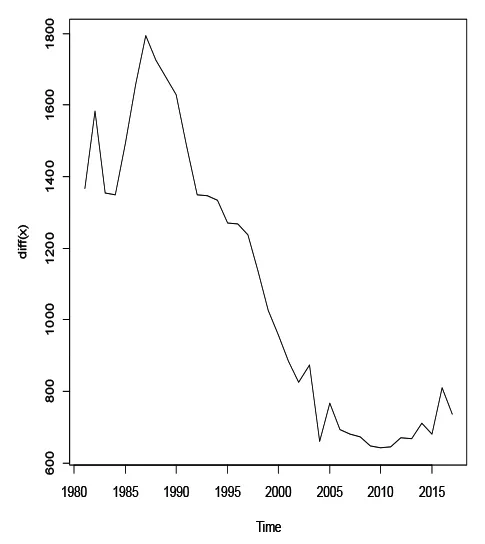
图3 一阶差分序列时序图

图4 二阶差分序列时序图
由图2知,序列呈上升趋势,即序列为非平稳。接下来通过ADF单位根检验,知其P值均比0.05大,故是非平稳序列。
2.2 对原序列进行差分,得到平稳序列
由图3、图4知,序列二阶差分后方为平稳序列,且经过ADF检验知其P值均比0.05小,故是平稳序列,与时序图直观显示出来的结果一致。
2.3 模型拟合及检验
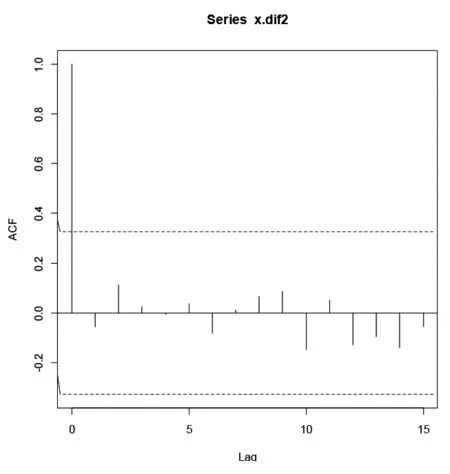
图5 自相关图
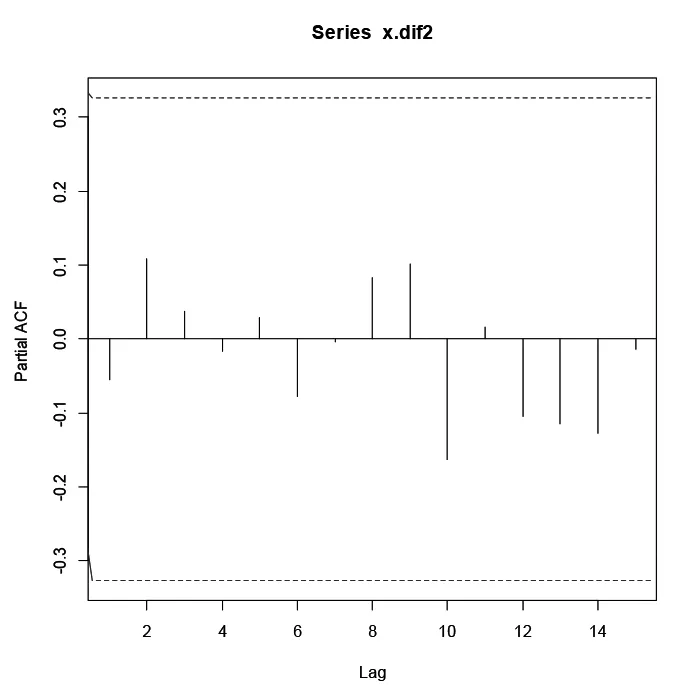
图6 偏自相关图
由图5及图6知二阶差分序列自相关图及偏自相关图均截尾,这与ARMA模型的定阶原则不相符。因此应尝试以下各种模型,并估计各模型的参数的参数,最后通过对比从中得到最佳模型。

表2 各拟合模型对比表
运用R软件可得表2所示数据,得AR(1)模型和MA(1)模型相对最优,且都能通过显著性检验,因此可以选用这两个模型来拟合该序列。
(四)预测
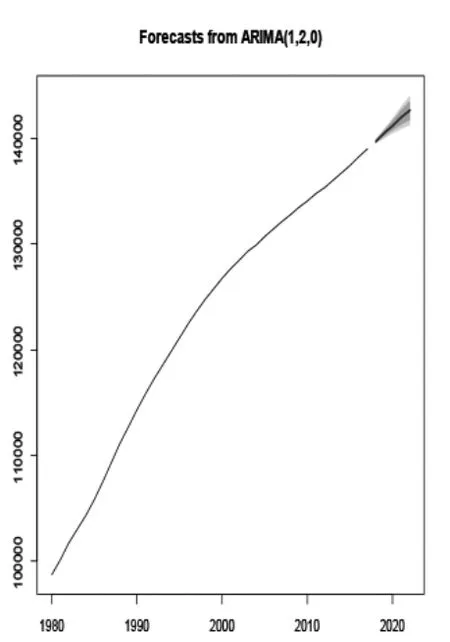
图7 AR(1)预测图
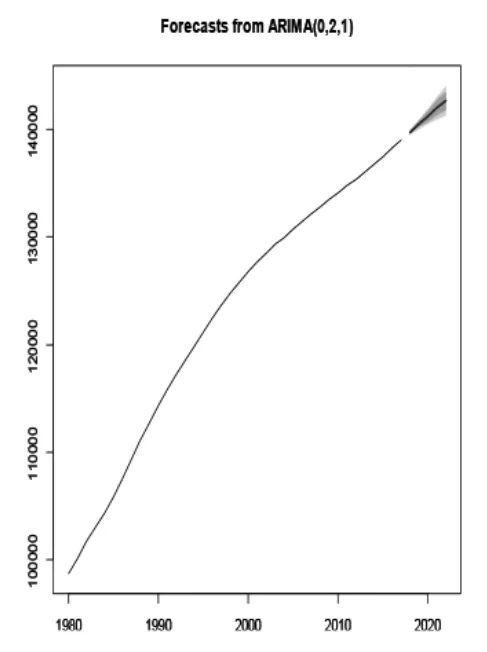
图8 MA(1)预测

表3 未来5年的预测值
图7给出由AR(1)模型预测得到我国未来五年的人口趋势图,图8为由MA(1)模型预测得到我国未来五年的人口趋势图,这两个图十分相似。表3为两个模型预测可得的具体人数,由表中数据可知,应用这两个模型预测差别不大。
3 结论及分析
对1980~2017年我国人口数据,应用时间序列分析中ARIMA模型,对我国人口问题进行预测。首先对原序列进行二阶差分后得到平稳序列;进而通过多个模型的对比,选用AR(1)模型和MA(1)模型来拟合该序列;最后运用模型进行了预测,发现这两个模型预测出的结果相差不大。确立的我国人口预测模型为
由预测结果可知我国未来5年内人口可能还会持续增长,这将使我们面临许多社会问题,比如住房困难问题、就业严峻问题、教育问题等。
