范德蒙矩阵形式下的病态线性方程组求解

王慧蓉，贾武艳

（长治学院 数学系，山西 长治 046011）

在许多科学和工程领域中，常常会遇到求解线性方程组的问题，而方程组解的准确性则由其性态所决定。病态线性方程组是在计算过程中经常要遇到的问题，因其系数矩阵的条件数很大，故会使得解严重失真。近年来，求解病态线性方程组的新算法不断推出，文献[1]采用了正则化方法求解病态方程组，文献[2]提出了病态问题的增广方程组法，文献[3]给出了精细积分解法等，并给出了一些数值例子来说明有较好的效果。但这些算法中选取的数值例子比较单一，大多数都以Hilbert矩阵为例来研究病态线性方程组，而针对系数矩阵为范德蒙德矩阵的研究相对较少。

文章选取以系数矩阵为范德蒙德矩阵的病态线性方程组，借鉴文献[4]提供的单参数迭代法和文献[5]中的新主元加权迭代法，对病态线性方程组进行分析求解。结果表明选取的迭代方法切实可行，对分析此病态线性方程组有很大帮助。

1 范德蒙德矩阵的病态性分析

选取n阶的范德蒙德矩阵如下：

估计其阶数与2-条件数的关系，分析其病态性。

表1 阶数n与条件数

由表1的数据可知，随着范德蒙德矩阵阶数的增加，其2-条件数也越来越大，病态性也越来越严重参见文献[6-7]。为更直观地了解阶数与条件数之间的关系，对条件数增长率进一步分析，如图1所示。

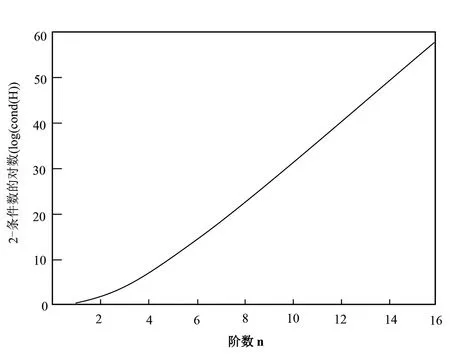
图1 2-条件数的对数（log（cond（H）））与阶数n的关系图

从图1中可以看出，当范德蒙德矩阵的阶数增加时，其对应的条件数在不断增加，病态程度也越严重。

2 单参数迭代法求解病态线性方程组

设病态线性方程组为：

其中系数矩阵A为范德蒙德矩阵，

即

对于上述线性方程组，取n=10，A的条件数为cond2（A）≈1.2×1014，可以看出此时矩阵A是严重病态的矩阵。用单参数迭代法对这个线性方程组进行求解，其中单参数迭代算法的参数ρ=1.000001（经过多次验证所得），得到表2的数值结果。

由表2可得：单参数迭代法对此病态线性方程组的求解效果比较好，迭代次数上有比较明显的优势，此方法对求解一般的病态方程组是非常有效的。

表2 解的近似值（n=10，ρ=1.000001）

3 新主元加权迭代法求解病态线性方程组

设病态线性方程组：

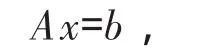
其中系数矩阵为范德蒙德矩阵，

下面用新主元加权迭代法对这个线性方程组进行求解，得到的结果如表3所示。

表3 解的近似值（n=10加权因子为ρ=1.000001）

由表3的数据可知，此方法相较于文献[4]和文献[8]中的方法，迭代次数明显减少，收敛速度也更快，解的精确度也非常高。在经过多次数值实验选取合适的加权因子后，对求解阶数不高时的病态线性方程组是有效的。

下面进一步分析加权因子取值的不同对此病态线性方程组解的影响。

表4 加权因子与绝对误差

从表4可以看出，对于加权因子ρ=0.0001，随着阶数的增加，绝对误差在增大。当阶数增加到12时，在重新选择ρ=0.0001的基础上，发现绝对误差继续增大，说明本方法还有待进一步改进。

4 结论

由上述研究结果可知，方法一（单参数迭代法）收敛速度快，是比较实用和有效的算法。方法二（新主元加权法）降低了矩阵的条件数，提高了收敛速度和精度。通过Mat l a b软件编程并运算以系数矩阵为范德蒙德矩阵的病态线性方程组可知，这两种方法都有较好的求解效果。但是对于矩阵元素过大的病态线性方程组，加权因子ρ应如何更合理地选取，还有待进一步研究，以提高算法的有效性。