球面惯性元件激光共焦曲率半径测量系统

邱丽荣，王超峰，赵维谦

（北京理工大学 光电学院，北京 100081）

球面惯性元件广泛应用于航空、航天、航海等领域的高精度惯性导航系统中。如半球型动压气体轴承是半球动压陀螺电机的核心部件，轴承的转动部分和静止部分被气膜隔离，没有接触磨擦是研制高精度、长寿命陀螺仪表的关键条件[1-2]。曲率半径作为其最基本的关键参数之一，精度将直接影响系统的综合性能。为满足精密装配的要求，需要准确测量元件曲率半径，然而这种具有散射特性的低反射率金属合金球型元件曲率半径的高精度测量一直是测量领域亟待解决的一个难点[3]。

目前元件曲率半径测量方法主要包括球径仪法、三坐标测量法、干涉仪法等[4-7]。对于常用的光学元件，干涉仪法具有很高的测量精度，该方法是通过对零干涉条纹的判读来确定猫眼和共焦位置，并测得两点之间的距离得到曲率半径[8]。但该方法对元件表面要求高，对于如金属合金材料的球面惯性元件，部分光被散射，而且一些惯性元件表面带有沟槽，返回光很难被聚焦于一点，干涉条纹质量差，无法实现高精度测量。因此，目前大多只能采用接触式方法来测量，如球径仪法、三坐标测量法。这两种方法在测量过程中测量头要与被测件发生接触[9]，因此易对被测件表面造成损伤，还会因球面元件的磨损或挤压产生测量误差。因此，上述测量方法不能起到指导加工装配的作用，球型元件的装配在很多情况下也仍只能靠工人手感，给轴承选配间隙带来了很大的误差。

本文基于激光共焦曲率半径测量方法[10]，通过针孔滤波以及共焦回馈增强技术抑制散射光的影响，结合气浮导轨平移台和激光干涉仪测长系统，研制了一套抗散射、非接触、高精度的球面惯性元件激光共焦曲率半径测量系统。推导出了相关光学理论模型，并以半球型动压气体轴承作为实验对象完成了实验。

理论分析和实验表明，系统能有效地抑制被测惯性元件表面散射光对曲率半径测量的影响，测量精度高，突破了传统非接触式方法对元件表面面型和材料反射率要求高的局限性，实现了对具有散射特性的低反射率金属合金球型元件的高精度无损伤检测，能够指导球型轴承元件的加工装配。

1 测量系统原理

测量系统结构如图1所示，主要包括三部分：共焦测量系统主机、被测元件装调和平移测量模块、主控系统。共焦测量系统主机，用来完成对测量数据的采集；被测元件装调和平移测量模块包括被测件五维调整机构、直线气浮导轨平移系统和激光测长系统以及环境补偿单元等，用来实现被测元件的装卡、平移、测距；主控系统用于实现对整个测量系统的控制以及对系统采集数据的处理。

图1 测量系统结构图Fig.1 The structure of measurement system

被测球面惯性元件装卡在五维调整架上并固定在气浮导轨的气浮滑块上，丝杠驱动气浮滑块带动被测元件沿光轴方向移动，然后根据返回光的共焦轴向光强响应曲线的峰值点，对被测元件猫眼和共焦位置精确定位，并用激光干涉仪对两位置之间的距离实现高精度测量，得到被测元件的曲率半径。

1.1 测量光路原理

如图2所示，点光源发出的球面波经过准直镜后成为平行光，随后被物镜会聚至焦点。当被测件位于猫眼位置时，被测件表面顶点与物镜焦点重合，测量光束会在被测件表面发生反射和散射而原路返回，被位于准直镜焦点处的探测器接收；当被测件位于共焦位置时，被测件球心位与物镜焦点重合，测量光束同样原路返回，被探测器接收。这样就可分别得到猫眼位置和共焦位置的共焦系统轴向强度响应曲线I(u)。

图2 测量光路原理Fig.2 Principle of optical path measurement

I1和I2两条共焦轴向光强响应曲线的峰值点分别对应被测元件的猫眼位置和共焦位置。使用激光测长测量干涉仪分别记录相应的坐标ZA和ZB，则被测元件的曲率半径为：

从图2可以看出，与其他曲率半径光学测量方法不同，本系统采用的是聚焦点的光强响应探测，可有效抑制散射光的影响，同时针孔滤波也进一步抑制了探测器对散射光的接收比例，进一步提升了系统的抗散射能力。共焦回馈光路增强了系统的返回光探测强度，使之可以适应因具有散射特性而反射率低的球面惯性元件的探测。

1.2 散射模型分析

如图3所示，当入射光光强为Ii，散射光在(θs,φs)方向上的光强分布为[11]：

其中，k=2π/λ为波矢量；θi为入射角；θs和φs为散射角；Q为物体表面的偏振因子；W(p,q)为物体表面轮廓的功率谱密度；p、q分别为x、y方向上的空间波数；dws=sinθsdθsdφs为立体角增量。

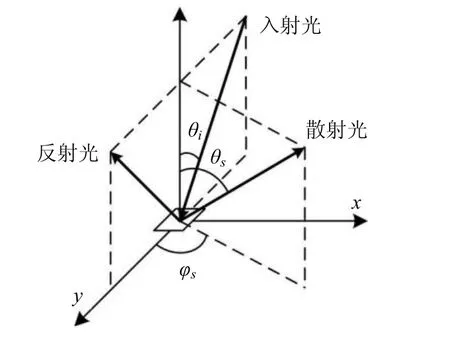
图3 散射模型Fig.3 scattering model

当被测件移动到猫眼位置附近时，假设测量光束都被散射或反射，聚焦点返回光的光场分布满足[12]：

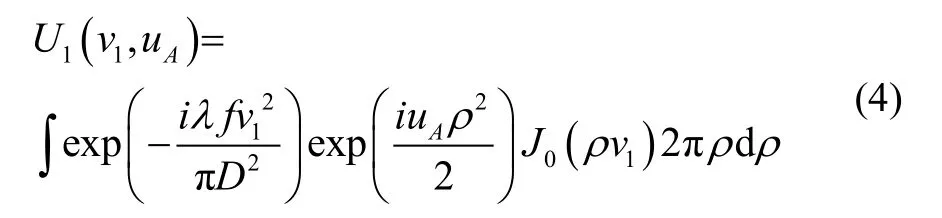
且

根据式(3)和式(6)可以仿真得到猫眼位置不同粗糙度下的的光强响应曲线I1(uA)，如图4所示。

当被测件移动的共焦位置附近时，球心位置的光场分布为：

则共焦位置球面上返回光的光场分布为：

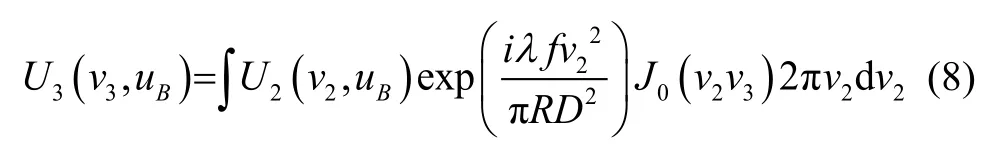
且

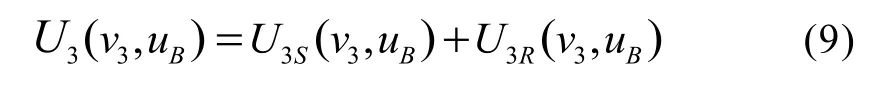
共焦位置球面上反射光以及散射光回到球心位置光场分布为：

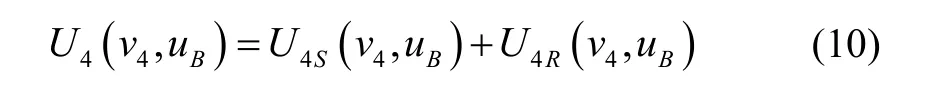
则可得被测件在共焦位置时，探测器的强度响应曲线I2：

图4 不同粗糙度值下猫眼位置的光强响应曲线Fig.4 Intensity response curves at cat's eye position for different roughness values

结合式(3)和式(11)可以仿真得到共焦位置不同粗糙度的光强响应曲线I2(uB)，如图5所示。

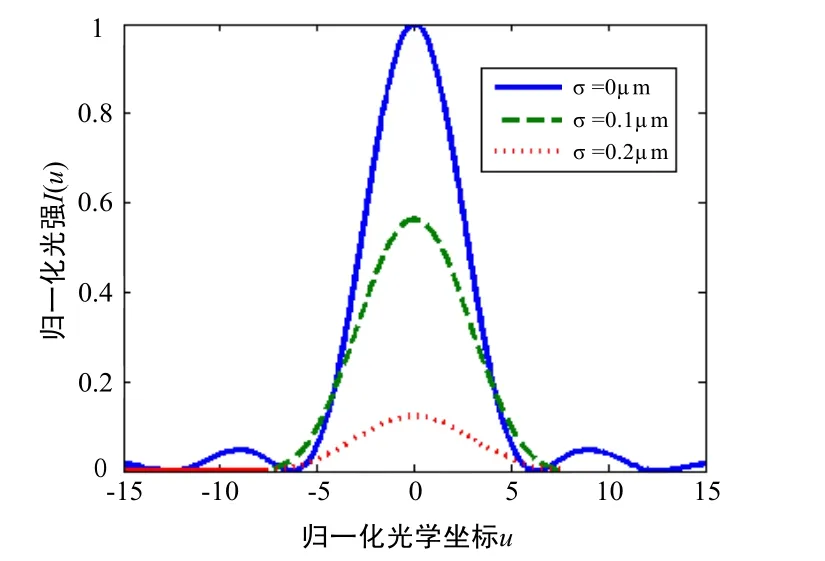
图5 不同粗糙度值下共焦位置的光强响应曲线Fig.5 Intensity response curves at confocal position for different roughness values

由图4和图5可以看出，随着被测件粗糙度的增加，散射光比例增加导致猫眼和共焦位置的最大归一化光强有所下降，半高宽有所增加。相比之下，共焦位置的最大归一化光强下降更快，当粗糙度等于0.2 μm时共焦位置最大归一化光强已经较小，测量时光强太小会影响测量精度，因此可以认为本系统能完成粗糙度小于0.2 μm的球面惯性元件的高精度测量。

1.3 环境补偿原理

系统使用的测长干涉仪是以激光波长为测量标准进行高准确度测量的仪器。因此，激光波长是系统测量精度的依据，然而在空气中传播的激光波长会受到空气折射率的影响，空气折射率则随着大气环境（包括气压、温度及湿度）的变化而变化，因此系统在测量过程中，需要实时测量大气环境的参数，用于对激光波长进行补偿，以此来校正环境变化对激光波长及长度测量的影响。

本系统的环境补偿单元包含有高灵敏度的温度、压力和相对湿度传感器，可对空气的温度、压力和相对湿度等参数进行测量，然后代入Edlen公式求出空气折射率变化量。Edlen公式微分形式如式(12)所示：

式中，t为环境温度，p为大气压力，f为空气中水蒸气压力。然后根据式(13)可以求出补偿后的实际波长：

式中，λ为实际波长，λ0为真空中激光波长，n0为真空折射率，△n为空气折射率变化量。

1.4 系统关键参数设计与优化

物镜数值孔径NA是系统的关键参数之一，直接影响系统的定焦灵敏度并决定系统性能。因此需要结合被测件实际情况对系统物镜的数值孔径NA进行优化设计选择。物镜数值孔径NA为D/f，将代入式(1)可得共焦轴向响应公式：

图6为根据式(14)仿真所得的NA取不同值时的共焦轴向光强响应曲线。

由图6可以看出，系统物镜NA值越大，共焦轴线响应曲线半高宽逐渐变小，系统定焦精度得到明显提高。但物镜口径一定的情况下，物镜NA越大，系统工作距离越小，可能会导致不满足测量条件。因此综合考虑被测件的实际情况以及各个因素，结合常用物镜参数，本系统选用数值孔径NA=1/1.5（D=100 mm，f=150 mm）的Zygo标准物镜。

图6 不同NA值共焦轴向光强响应曲线Fig.6 Confocal axial response curves with different NA

2 系统构建

2.1 系统结构

根据图1所示测量系统结构示意图，设计并研制了如图7所示的球面惯性元件激光共焦曲率半径测量系统。测量系统主要由共焦测量系统主机、被测元件装调和平移测量系统、主控系统构成。其中：系统物镜选用 Zygo公司生产的口径D=100 mm、焦距f=150 mm的标准物镜；精密直线气浮导轨平移系统选用课题组自主研发的全长为 1200 mm、有效行程为900 mm、直线度为1 μm的高精度余气可回收式气浮导轨；激光测长系统选用英国Renishaw公司生产的XL-80型激光测长干涉仪，测量精度约为0.5×10-6。测量系统放置在气浮隔振光学平台上，避免振动对测量结果的影响，提高系统测量精度。为减小阿贝误差，系统采用同轴结构设计，即共焦光路、干涉仪测长光路以及被测元件的光轴必须位于同一直线上。

图7 测量系统实物图Fig.7 measurement system

2.2 系统软件

系统软件使用 C++语言进行开发，开发环境为Microsoft Visual Studio 2010，采用MFC应用程序框架，多线程技术结合 GDI+技术实现实时测量和数据处理模块的功能。根据系统工作方式以及各硬件结构，将系统软件结构设计为如图8所示的硬件控制结构。

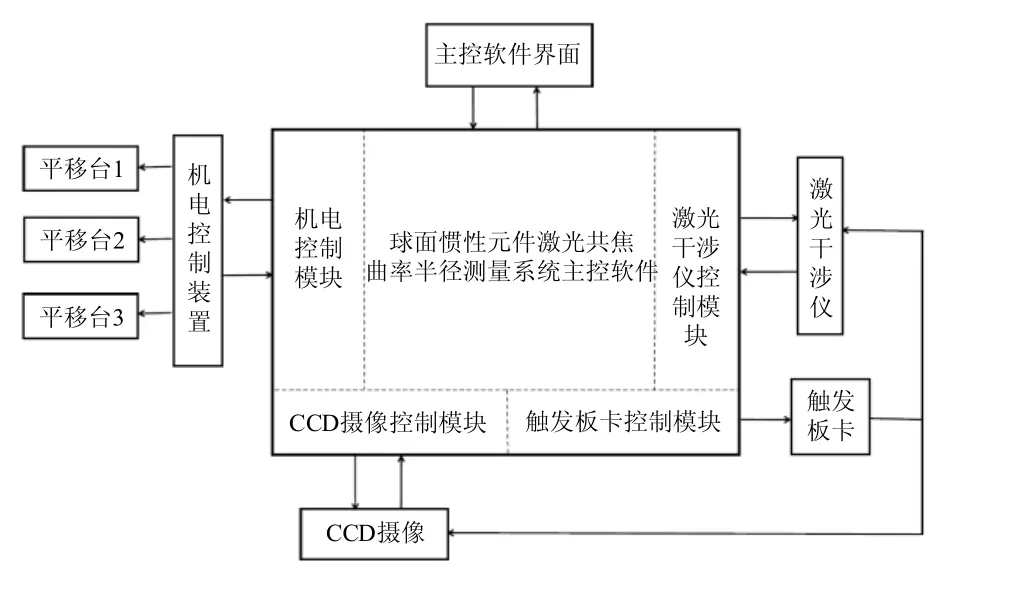
图8 测量系统软件结构Fig.8 Software structure of measurement system

系统主要包含机电控制、CCD摄像机控制、触发板卡控制及激光干涉仪控制四个模块。机电控制模块主要通过串口实现与机电装置之间的通信，对各路电机进行控制；CCD摄像机控制模块主要完成对 CCD摄像机的初始化、图像实时采集的控制以及参数调整，图像信息存储；触发板卡控制模块主要对I/O触发板卡进行控制，进而控制 CCD摄像机与干涉仪同步采集数据；激光干涉仪模块主要完成激光干涉仪的初始化以及干涉仪测得数据的调用传输。

系统软件主要有实时测量显示和测量数据处理两个界面。实时测量显示界面主要功能是硬件参数设置与测量结果的实时显示。测量数据处理界面主要完成测量系统各个数据处理模块之间的实现与交互，具有干涉仪读数、光斑图像处理、共焦曲线显示、测量数据打开与存储等功能。

3 系统不确定度评定

对系统测量结果产生影响的主要误差源有激光干涉仪测长误差、被测元件面型误差、系统各轴线不重合引起的偏差、系统定焦的随机误差等。这些误差源都会引起测量不确定度分量。

3.1 干涉仪测长误差引起的不确定度分量

系统中的激光测长系统选用英国Renishaw公司生产的XL-80 型激光测长干涉仪，测量精度约为0.5×10-6（k=2），因此由干涉仪测长误差引起的标准不确定度分量为：

3.2 被测件面型误差引起的不确定度分量

由于被测表面面形的影响，猫眼与共焦位置对应的区域通常与被测表面的最佳球面不重合，就会引入面形误差σfigure：

式中PV是被测件的表面面型。因此，由被测件面型误差引起的不确定度分量：

3.3 轴线不重合误差引起的不确定度分量

在元件曲率半径测量的过程中，运动平移台直线度很高可近似认为是直线运行。理想情况下，其运动方向应该与测长干涉仪的轴线以及被测元件的轴线平行，但实际上三者之间两两存在一个夹角，会对曲率半径测量造成影响。假设被测元件的轴线与运动平移台轴线之间的夹角为θ，运动平移台轴线与测长干涉仪轴线之间的夹角定义为γ，则可以得到由于轴线不重合引起的曲率半径测量误差：

由于系统具有精密调整机构，θ和γ角都可通过调整被测元件姿态以及激光干涉仪测量轴线来减小，经实际验证θ和γ的调整精度都可以控制在2″以内。由轴线不重合误差引起的不确定度分量为：

3.4 探测器离焦量引起的不确定度分量

理论上，探测器需要精确定位在焦点位置。但在实际情况中，探测器位置很难精确调整，会存在一定偏差δM，这就会导致系统在猫眼和共焦位置共焦轴向光强响应峰值也有一定的偏移△uA和△uB，轴向光强响应曲线会有以下变化：

根据式(20)和式(21)，猫眼和共焦位置共焦轴向光强响应峰值偏移量：

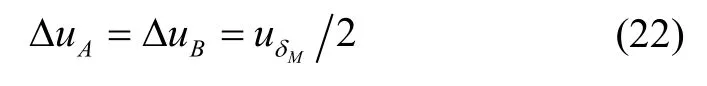
由探测器偏移引起的猫眼和共焦位置的轴向光强响应峰值偏移量ΔuA和ΔuB完全相同。结合测量原理可知，探测器偏移对曲率半径测量结果没有影响，因此，探测器离焦量引起的不确定度分量可忽略不计。

3.5 不确定度合成

除上述几项误差外，系统中还存在一些其他随机误差，比如猫眼和共焦位置的定焦误差。这些随机误差引起的不确定度分量u4可通过多次重复测量获得。综合以上几项误差源对测量结果的影响，合成标准不确定度uc为：

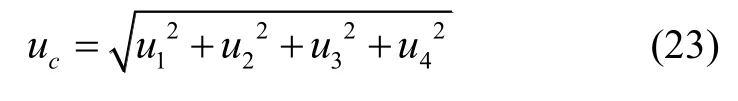
4 实验验证

选用图9所示的球面惯性元件在图7所示的球面惯性元件激光共焦曲率半径测量系统上进行实验。

实验在室温(20±1)℃，湿度约40%的环境中进行。图10为第一次测量被测件得到的猫眼位置ZA和共焦位置的ZB光强响应曲线。通过主控软件数据处理后得到ZA= -7.500 938 mm，ZB= -0.002 432 mm，则曲率半径为R=ZB-ZA=7.498 507 mm。

在同一条件下，对被测件进行多次曲率半径测量，测量结果如图11所示。10次测量结果的平均值为7.498 432 mm，测量不确定度u4=0.064 μm。

图9 被测球面惯性元件Fig.9 Measured spherical inertial element

图10 猫眼和共焦位置的光强响应曲线Fig.10 Intensity response curve

根据式(15)～(23)可得系统合成标准不确定度：

扩展不确定度：

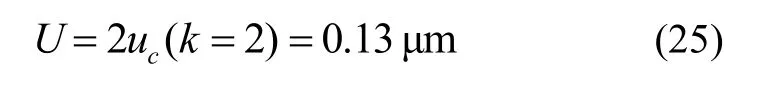
相对扩展不确定度：

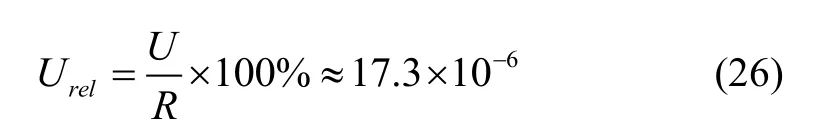
图11 曲率半径测量结果Fig.11 Radius measurement results

实验结果表明，系统测量球面惯性元件曲率半径的相对扩展不确定度优于20×10-6。

5 结 论

本文研制的球面惯性元件激光共焦曲率半径测量系统，通过针孔滤波技术抑制散射光的影响，并通过共焦回馈技术增强光强探测强度，实现了具有散射特性的低反射率元件的探测，利用激光定焦技术确定猫眼位置和共焦位置，通过测长干涉仪精确测长，继而实现曲率半径的测量。理论分析和实验结果表明，系统相对扩展不确定度优于20×10-6，满足高精度曲率半径测量需求。实现了球面惯性元件曲率半径的高精度无损伤测量，为具有散射特性的低反射率球面惯性元件曲率半径的高精度测量提供了技术途径，可以指导球型元件的超精密加工，确保装配合格率。