基于改进高斯和粒子滤波的海底地形辅助导航

程向红，范时秒

（1.微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2.东南大学 仪器科学与工程学院，南京 210096）

水下航行器是进行海洋资源探测的重要工具之一，精准导航定位是其完成水下作业的关键。地球物理量场（地形、地磁、重力）辅助导航最早应用于航空和陆地导航领域，后被引入水下导航[1]。相较于地磁场和重力场，水下地形具有时不变性和局部唯一性，通过实时测量的水深数据与真实海图数据库进行相关性分析，结合惯性导航系统实现水下航行器导航定位[2]。

海底地形辅助导航定位问题属于状态估计问题，从算法角度来看，常见的处理方法分为批处理算法和序贯性处理算法[3]。批处理算法以地形轮廓匹配法和地形最近点迭代法为代表，将海底地形数据经过一段时间的采集累积，形成海底地形序列，再与海图数据库进行分析得到载体匹配位置，这一匹配位置作为导航系统的观测量，修正惯性导航系统数据并最终得到载体位置输出值[4-5]。序贯性处理算法则是每采集得到一个水深观测值，就实时更新辅助导航系统状态，这种方法更有效地利用了水深观测数据实现匹配定位，主要方法包括应用扩展卡尔曼滤波器和应用贝叶斯估计器两大类型，粒子滤波是序贯性处理算法的代表性算法[6-7]。

粒子滤波（Particle Filter,PF）是一种基于蒙特卡洛的贝叶斯估计方法，不需要对地形数据进行线性化处理。瑞典学者Bergman最早将基本粒子滤波引入航空领域的地形辅助导航系统，建立贝叶斯框架下的地形辅助导航框架，完成了理论推理与有效性验证[8]。由于粒子滤波存在粒子匮乏的问题，文献[9]和文献[10]先后提出了高斯粒子滤波以及高斯和粒子滤波，用高斯概率密度逼近系统后验概率分布，有效估计系统状态。高斯和粒子滤波相较于基本粒子滤波算法，不需要进行粒子重采样过程，文献[11]将径向基函数神经网络与高斯和粒子滤波器相结合，引入水下地形辅助导航系统。但是由于水下航行器航行速度较慢，当海图精度低时，得到的海图有效信息较少，系统后验概率估计不准确。

本文针对低分辨率海图下水下地形辅助导航定位精度较低且基本高斯和粒子滤波计算量较大的问题，提出了一种基于改进高斯和粒子滤波（Improved Gaussian Sum Particle Filter,IGSPF）的海底地形辅助导航方法，采用高斯过程回归（Gaussian Process Regression,GPR)方法实时建立海底地形精细模型，在基本高斯和粒子滤波的基础上引入最小均方误差约束求取高斯和项中的最优粒子状态，有效提升水下航行器导航定位精度和算法效率。

1 海底地形辅助导航系统模型

海底地形辅助导航系统主要包括海底地形数据库、惯性测量单元和水深测量单元。海底地形数据库存储航行区域海底地形图数据，惯性测量单元提供估计状态基准，水深测量单元实时采集水深数据。

状态方程为

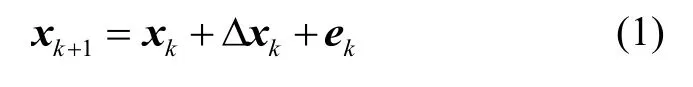
式中：xk和xk+1分别为k时刻和k+1时刻的状态，取ξ、η分别为水下载体所处位置的纬度、经度，为航行器距海平面的下潜深度（水深值与航行器距海底距离之差），H、P、R分别为水下载体的航向角、俯仰角、横滚角，εx、εy、εz分别为载体坐标系下x轴、y轴、z轴的陀螺随机常值漂移；ek为过程噪声，其统计特性是均值为零，方差为Qk的高斯分布，ek～N(0,Qk)；Δxk是从k时刻到k+1时刻的一步预测增量，如式(2)所示。

式中，Hk、Pk、Rk分别为k时刻水下载体的航向角、俯仰角、横滚角；Ψ(Hk,Pk,Rk)为从载体坐标系到导航坐标系变换的姿态矩阵；vk为载体速度；Δt为滤波周期；分别为k时刻载体坐标系相对于导航坐标系的角速率沿载体坐标系x、y、z轴方向的输出值。

观测方程为

2 海底地形精细建模

海底地形数据库是地形辅助导航系统的基础，高精度的海底地形模型是精确导航的前提。由于电磁波在水中快速衰减，全球卫星导航系统信号较差，因此与陆地测绘相比，水下测绘难度较大，目前公开的海底地形数据库精度低于航空导航地形数据库。常用的海图数据库采用的是离散非线性的规则格网数字高程模型（Regular Grid-Digital Terrain Model,GRID-DTM），当采样点不位于网格点时，常采用线性插值法计算采样点的海图深度值。但是如果海图分辨率较低（大于30 m），线性插值法误差较大。

本文采用高斯过程回归建立局部地形精细模型。高斯过程回归是一种有严格统计学基础的机器学习训练方法，通过训练样本数据，建立样本输入和样本输出之间的关系以生成高斯过程模型并预测实际输入对应的输出，高斯过程回归特性主要取决于均值函数和协方差函数[12-13]。

假设海图中某点的水平位置p0=[ξ0,η0]，以p0为中心，mgrid代表m个网格，在水下海图中选取处于{α∈(ξ0-mgrid,ξ0+mgrid)，β∈(η0-mgrid,η0+mgrid)}中的τ个节点，以τ个节点的水平位置向量px=[α,β]及对应的地形数据hpx作为p0处精细地形模型的训练数据，建立基于高斯过程的水下地形模型以求取p0位置的水深值。

选取协方差函数为

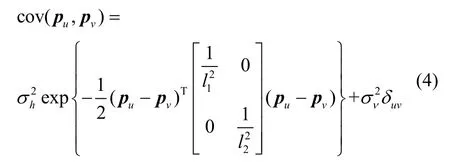
式中，pu和pv为训练样本水平位置向量的任意元素，cov(·)是协方差函数，σh是地形数据标准差，σv是样本噪声标准差，l1是地形模型水平尺度，l2是地形模型垂直尺度。当u=v时，δuv=1；当u≠v时，δuv=0。

训练样本的条件概率对数似然函数为：

式中，K(px,px)为τ×τ阶协方差矩阵，且计算公式为K(px,px)={cov(pu,pv)|u,v=1,2,…,τ}。Iτ为τ维单位矩阵，p(·)为概率。

定义Θ={σh,σv,l1,l2}为协方差函数的超参数，超参数估计值为：

由此，可得到p0处的高度值为

式中，K(p0,px)为水平位置向量p0和px之间的1×τ阶协方差矩阵。

本文在高斯和粒子滤波中读取采样粒子位置处的海图水深值时采用上述方法，基于高斯过程的海底地形精细建模步骤为：

步骤1：选取训练样本。以需要读取海图数据的某点水平位置为中心，若该点不位于海图节点，选取周围m×mgrid2中的所有海图节点及对应的水深值为训练样本，本文中取m=5。

步骤2：根据式(4)选取协方差函数，根据式(5)计算训练样本的条件概率对数似然函数。

步骤3：根据式(6)求取超参数估计值，完成海底地形精细建模，并根据式(7)给出该点水深估计值。

3 改进高斯和粒子滤波

高斯和粒子滤波是将高斯和滤波与粒子滤波结合的非线性滤波方法，当系统为非线性系统时，以有限个高斯概率密度和逼近状态的后验分布，提升系统滤波性能。针对基本高斯和粒子滤波计算量大，算法复杂度较高的问题，本文提出改进高斯和粒子滤波。

3.1 高斯和粒子滤波

高斯和粒子滤波的主要思想为：根据先验信息初始化高斯和项及相应的粒子信息，通过系统状态更新方程计算粒子下一时刻状态，将粒子计算观测值与实时采集的观测值进行相关性分析，计算得到该粒子的权值，从而得到每个高斯和项的权值与方差并给出最终的后验分布[10]。

假设在k-1时刻，已得到预测分布

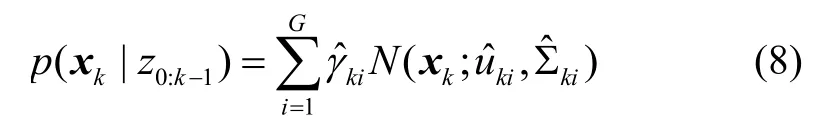
其中，G为高斯和项的个数，分别是由先验信息得到的第i个高斯和项的权值、均值和方差，N(·)为高斯分布。

在k时刻，采集到这一时刻的观测值，滤波概率分布更新为

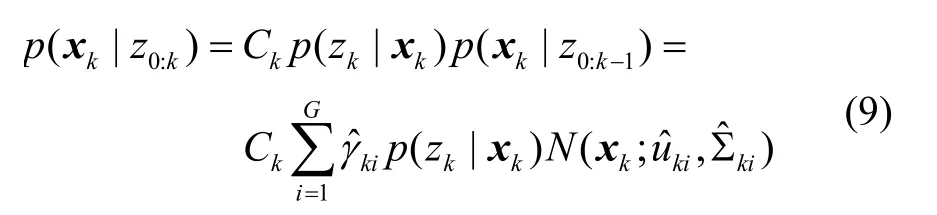
式中，Ck为比例常数。

根据高斯和原理[10]，任何概率分布都可用多个高斯分布加权和近似，在p(xk|z0:k)中抽样得到 样本粒子的权值为

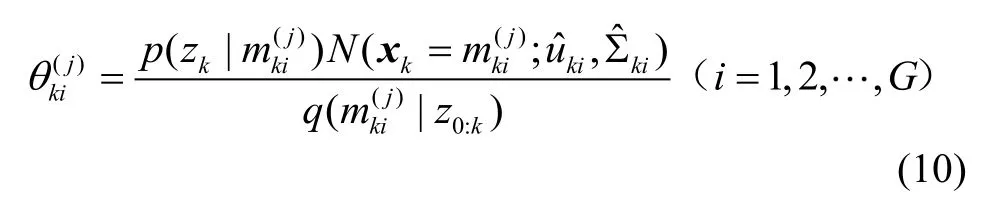
均值

方差

高斯和项的权值及归一化如式(13)和(14)所示：

由此，滤波概率分布近似为

由k时刻的概率分布可得到k+1时刻的预测分布为

其中，

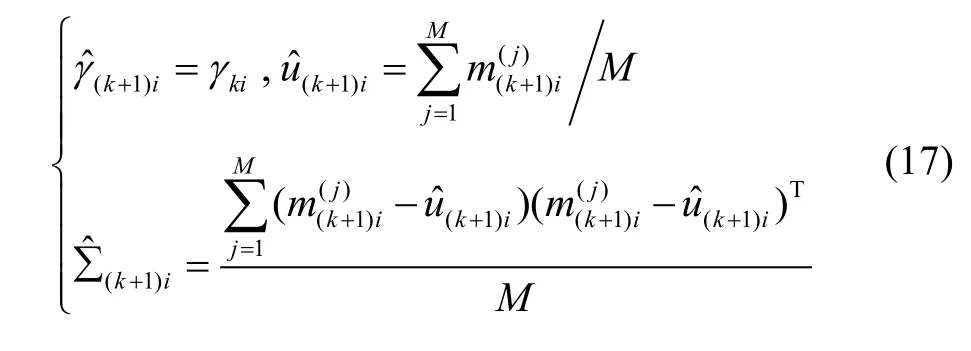
3.2 算法改进思路

由高斯和粒子滤波的主要思想可知，如何准确逼近系统后验概率的真实分布是整个算法的关键，算法的核心参数是计算每个粒子的权值粒子权值影响最终的预测输出。当系统非线性较强时，高斯和粒子滤波的高斯和分量和粒子数增加，滤波更新算法复杂度较高。因此，本文在量测更新阶段引入最小均方误差约束，在降低算法复杂度的前提下提升算法精度。

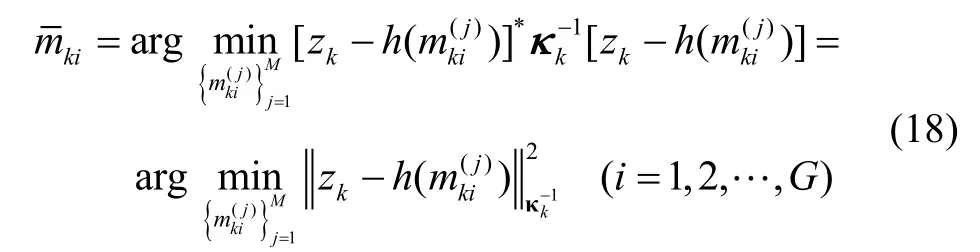
其中，形如||X||A的范数表示的值，κk为观测向量生成的相关性矩阵，κk(i,j)为观测量i与观测量j的相关性系数，指的是通过本文第2部分所述建模方法求取的粒子状态的参考观测值，arg min代表使表达式达到最小值时的变量取值。

引入上述约束之后，量测更新的式(10)～(15)更新为式(19)～(25)，算法涉及的重要参数计算过程得到简化。从原理上分析，寻求的粒子状态为每个高斯和项的最优粒子状态，减少了较差粒子状态的影响，因此算法估计精度会有所提升。

高斯和项的权值及归一化

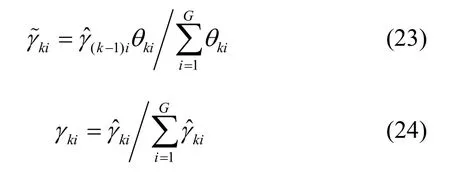
最终滤波概率分布近似为

4 基于IGSPF的海底地形辅助导航流程

本文提出的改进高斯和粒子滤波主要针对算法量测更新阶段进行改进，基于改进高斯和粒子滤波的海底地形辅助导航方法的整体步骤如下：

步骤1：进入地形匹配区后，初始化G个高斯和项，每个高斯和项中初始化M个粒子，粒子初始化范围[3]是以惯性器件指示位置为中心的误差椭圆外切矩阵。

步骤2：当得到新的量测量zk时，在p(xk|z0:k)中抽样得到，以本文第 2部分所述建模方法，计算采样粒子处的水深值根据式(18)以MMSE约束计算每个高斯和项的最优粒子状态

步骤3：根据式(19)～(25)计算高斯和项的权值、均值和方差，求取p(xk|z0:k)。

步骤4：根据式(1)，对粒子进行状态转移，得到根据式(16)(17)，由k时刻的概率分布估计k+1时刻的预测分布p(xk+1|z0:k)，输出导航状态估计值。

步骤5：重复步骤2～4，直至地形辅助导航结束。

5 仿真与分析

为了验证本文所提方法的有效性，在 MATLAB R2016a 平台下进行仿真对比实验，实验海图选择某海域10 m分辨率海图数据，以海图区域左下角为原点绘制航行区域海图。

水下航行器采用经典观测路径“割草机路径”[14]，航行速度为4 kn，起始点水平位置为(1116 m,375 m），航行路径先经过等深线稀疏区域，再进入等深线稠密区域。设置水深值采样频率为1 s，惯性器件采样频率为10 ms。海底地形辅助导航仿真参数如表1所示。

表1 海底地形辅助导航仿真参数Tab.1 Simulation parameters of seabed terrain aided navigation

粒子滤波、高斯和粒子滤波和改进高斯和粒子滤波的粒子初始化范围为250 m ×250 m ，粒子滤波的粒子数为M=1000，高斯和粒子滤波和改进高斯和粒子滤波的高斯和项数目G=30，每个高斯和项中选择的粒子数M=30。高斯过程回归的超参数初值设置为Θ={1,0.01,10,10}。

在同一仿真条件下进行仿真实验对比四种算法，分别是：①采用双线性插值建模的粒子滤波导航算法；②采用GPR建模的粒子滤波导航算法；③采用GPR建模的高斯和粒子滤波导航算法；④本文提出的采用GPR建模的改进高斯和粒子滤波导航算法。

仿真结果如图1～4所示。图1为海底地形辅助导航仿真轨迹；图2～4分别为四种算法仿真的水平位置误差、北向位置误差和东向位置误差图。算法①～算法④的平均水平位置误差分别为40.3 m、25.5 m、15.2 m和12.2 m。由图1～4可知，将算法①和算法②对比，在低分辨率海图下采用高斯过程回归建立精细模型能提升整体定位精度。将算法②、算法③和算法④对比，在低分辨率海图下，本文所提出的改进高斯和粒子滤波方法定位误差精度高，收敛速度快，计算轨迹更接近于水下航行器真实轨迹（橙色直线）。

从仿真图中还可以看到，本文提出的IGSPF算法在0～500 s的位置误差明显大于500～1200 s之间的位置误差。出现这个现象的原因有两个方面：一方面是因为水下航行器在航行开始阶段存在初始误差；另一方面是因为在0～500 s的航行区域为等深线稀疏区域，500～1200 s航行区域为等深线稠密区域，等深线稀疏代表地势平坦，定位难度会相对较大。从这个现象也可以反映本文所提算法既适用于陡峭区域，也适用于平坦区域。

图1 海底地形辅助导航仿真轨迹Fig.1 Seabed terrain aided navigation simulation trajectory

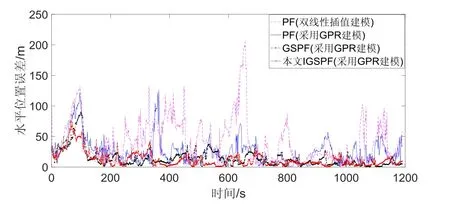
图2 水平位置误差Fig.2 Horizontal position errors

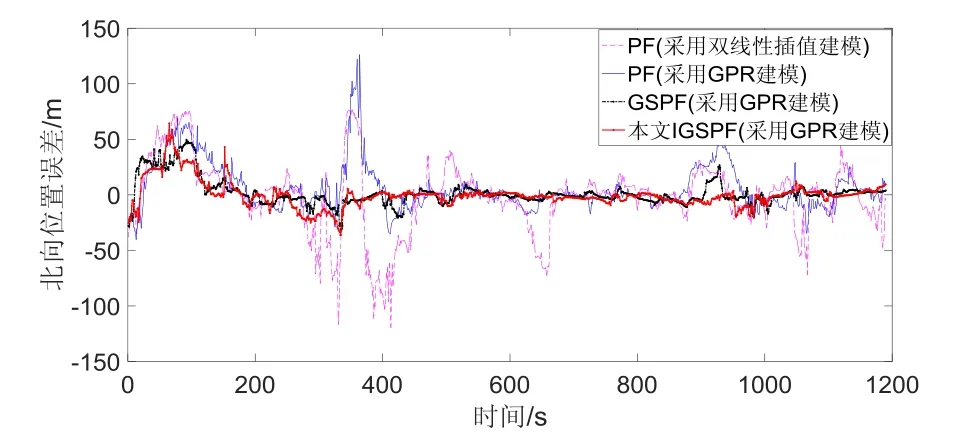
图3 北向位置误差Fig.3 North position errors

图4 东向位置误差Fig.4 East position errors

为了进一步验证算法，在高斯过程回归建模的前提下，采用PF、GSPF和IGSPF分别进行了50次蒙特卡洛实验，实验统计数据如表2所示。采用PF、GSPF和IGSPF时系统水平位置误差均值分别为25.1 m、14.5 m和10.2 m，全程匹配时长分别为35.6 s、30.9 s和20.2 s。此外，统计了在等深线稀疏区（即平坦区）的仿真结果，水平位置误差均值分别为35.2 m、22.3 m和16.3 m，与等深线稠密区相比位置误差有所增大，但是本文所提出的IGSPF方法的定位误差能保持在1.5个网格量级左右。由仿真实验结果可知，本文所提算法与采用基本粒子滤波和基本高斯和粒子滤波的海底地形辅助导航方法相比，导航定位精度提升了20%～40%，算法耗时降低了30%～40%，在提高导航定位精度的前提下降低了算法复杂度。

表2 蒙特卡洛实验仿真结果Tab.2 Results of Monte Carlo simulations

为了进一步验证本文所提算法在等深线稀疏区域导航的有效性和可靠性，在平坦海域进行仿真实验，起点为（2782 m,352 m），其它仿真条件与上述实验相同。仿真路径和最终的仿真结果如图5～6所示。在平坦区域实验中，由于海底地形辅助导航初期存在初始位置误差，仿真轨迹误差较大，水平位置误差较上一实验有所增加，但是仿真后期轨迹也快速收敛至真实轨迹附近，证明了本文所提算法在等深线稀疏区域的有效性。

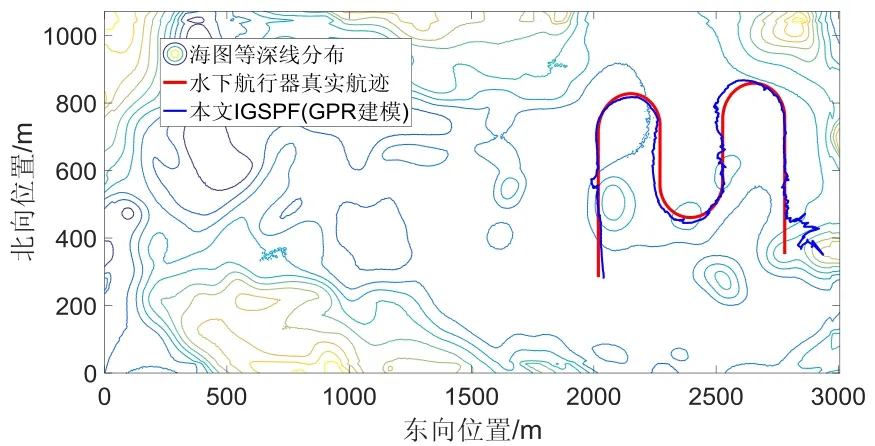
图5 等深线稀疏区域导航仿真轨迹Fig.5 Navigation simulation trajectory in flat area

图6 位置误差示意图Fig.6 Diagram of position errors in flat area

6 结 论

本文针对低分辨率海图下水下航行器导航定位问题，提出基于改进高斯和粒子滤波的海底地形辅助导航方法。利用高斯过程回归在非线性模型下建模准确的特点，结合高斯和粒子滤波预测优的性能，在量测更新阶段引入最小均方误差约束。

仿真结果表明，该算法相较于采用基本粒子滤波和基本高斯和粒子滤波的海底地形辅助导航系统，可有效提升水下导航定位精度，提升导航效率。本文所提出的方法普适性强，在地形陡峭区域和平坦区域均可应用。此外，该方法既可以应用于低分辨率海图下的海底地形辅助导航系统，后期也可拓展至其它水下地球物理量（地磁/重力）辅助导航系统。