基于数据分析的课堂教学质量网络评教模式研究——以玉溪师范学院为例

张 俊，羊 波，胡杨升

(玉溪师范学院，云南 玉溪 653100)

1 研究背景

自1999年党中央国务院作出“扩大高等教育规模”的重大决策，我国实施科教兴国、人才强国战略以来，我国的高等教育规模迅速扩大，先后超越俄罗斯、印度和美国，成为世界第一，成功实现了从“精英教育”到“大众教育”的转变。作为人才培养高地，高等教育承担着培养高素质人才、发展先进科技和促进现代化教育的重要使命[1]。但随着高校扩招政策的不断推进和招生人数的急剧增加，师资资源紧张、教学资源无法满足教学需求等现象日趋明显，数量的扩张影响着质量的变化，使高等学校的教学质量面临着严峻挑战[2]。因此，如何提高高等学校办学水平和教学质量一直是社会各界普遍关注的问题，也是21世纪我国高等学校改革和发展的根本问题[3]。

玉溪师范学院作为玉溪市唯一的一所高等教育院校，一直致力于提高教学质量的工作，尤其重视每学年必须开展的评教工作。评教工作实施是以学生评教为主，督导、同行教师和教师自评为辅，其中学生评教工作量最大、开展难度较高，同时学生评教也是其最重要的部分，因为它对学校的教师教学工作具有直观效应，能最直接地反映出教师教学的效果。所以，工作量极大的学生评教工作亟需进行创新和改革，以促进教育教学质量的发展。

依托网络评教系统，改变以往纸质评教的传统操作方式，提高评教的工作效率，简化工作流程，以获得一个合理准确和公正公平的评价结果及意见。评价结果和意见可为教师进行教学完善、教学改进提供参考依据，提高教学质量。对评教结果从不同方向进行数据挖掘，能更全方位地、更深入地从评教结果中发现问题，从而对教师的教学水平与能力认定有更好的数据支撑，对教师教学水平的自我完善具有更长远的指导意义。

2 研究对象

玉溪师范学院于20世纪90年代初期就开始了对教师教学评价的探索，从最初的纸质评教到2016年实行网络化评教，积累了大量学生评教数据，为本研究的开展提供了良好的课堂教学质量数据基础。从学生角度出发，设计了相应指标内容。整个课堂教学质量评估表主要从教学态度、教学内容、教学方法和教学效果4个方向进行评价，每个方向又分为5个评价指标，不仅评价了教师的教学行为，也评价了学生的学习收获[4]。玉溪师范学院课堂教学质量评估如表1所示。

3 数据分析

为了改变传统的评教操作方式，提高评教的工作效率，简化工作流程，以获得一个合理准确和公正公平的评价结果，用其指导教师完善今后的教学方向，提高教学质量[5]。对评教结果分不同方向进行数据挖掘，能更深入地从评教结果中发现问题，对教师的教学水平与能力认定有更好的依据，对教师的教学水平自我完善具有更长远的指导意义。本研究的数据来自玉溪师范学院教学评价管理系统，由于数据量巨大，故仅分析了2017-2018学年下学期81门课程的学生评教数据。在分析过程中，首先对原始数据进行处理，剔除不合理数据，再应用方差分析法、聚类分析法和主成分分析法进行分析总结。

表1 玉溪师范学院课堂教学质量评估

3.1 方差分析

以班级和课程领域两个因素为出发点，利用方差分析法探究评教结果的影响因素，并从这些因素所造成不同评教结果的影响程度，分析教师教学或教学课堂中存在的主要问题。

3.1.1 不同班级对同一教师同一课程的评教结果差异性挖掘

以自然班级物理本科15-1和15-2班同一课程的任课教师(杨教师)的获评结果信息为例，用方差分析法对评教结果进行数据信息挖掘，对比分析两个自然班级对杨教师评教的20个评价指标中评教的差异程度，其数据信息挖掘结果如表2所示。

从表2数据分析结论可以看出，两个自然班级在对杨教师的课程评教中，大部分指标评教结果差异较小。同时，通过方差分析方式，对其他相同情形的任课教师的评教数据结果挖掘分析后，也得到了类似结论。数据显示，不同班级对同一任课教师同一门课程的评教结果差异性较小。从方差分析方式出发，以数据信息为依托，就可简单、快速地了解到学生对任课教师的教学评价。

3.1.2 同一教师在同一领域内的课程评教结果差异挖掘

该部分以物理学科不同课程(普通物理综合性、设计性实验和普通物理实验Ⅲ)周教师的获评结果为例，对同一教师同一领域内的不同课程获评结果进行数据挖掘分析(由于上文分析已经得到了不同班级对同一教师同一门课程的评教结果差异性小，因此，可以把所有班级看成等同)，其数据信息挖掘结果如表3所示。

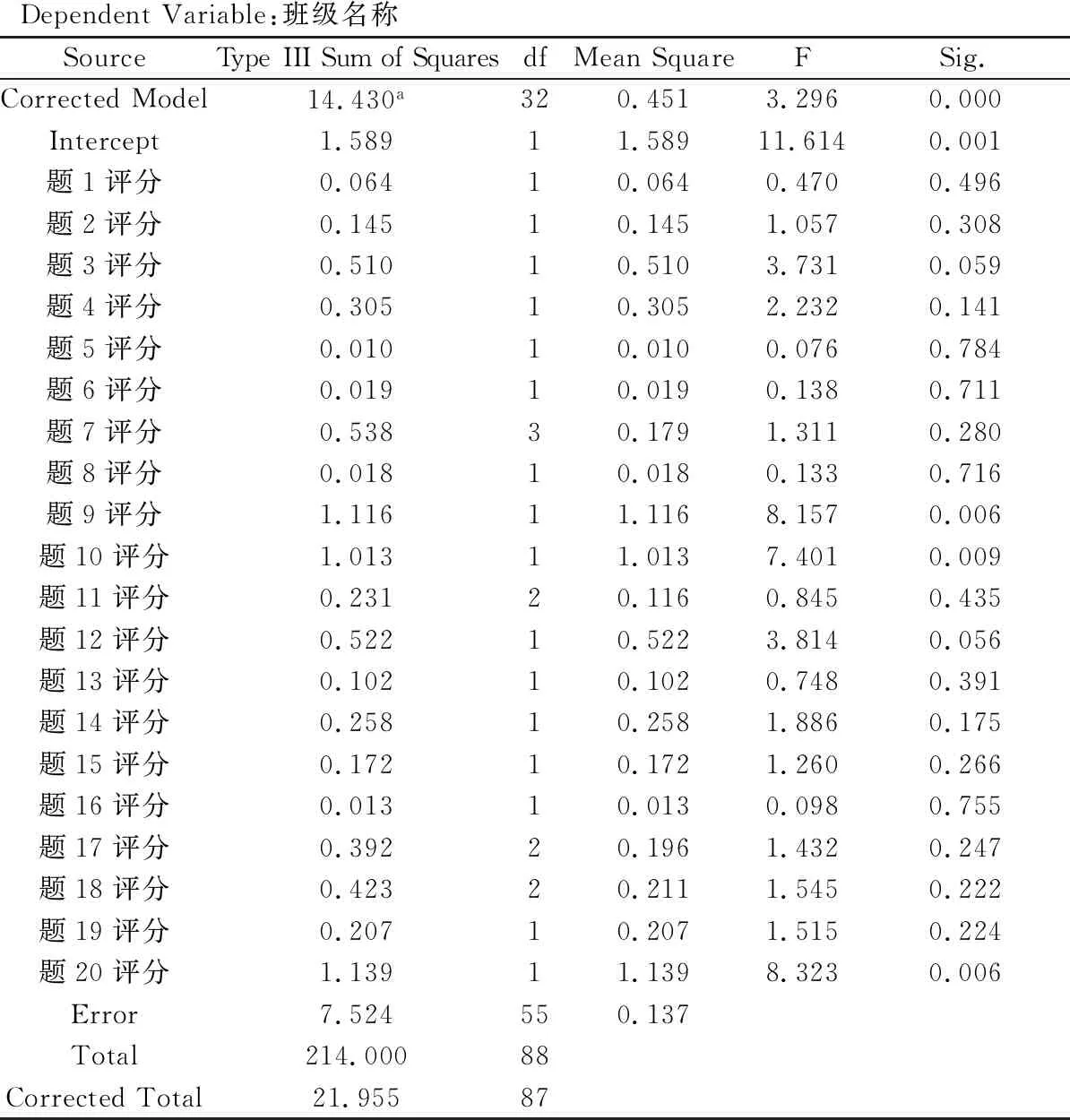
表2 方差分析(一)

a. R Squared=0.657(Adjusted R Squared=0.458)

表3 方差分析(二)

a. R Squared=0.612 (Adjusted R Squared=0.445)

从表3中可以看出，除题7和题16指标的评分外，其余评分指标的差异程度均不显著。同时，也对其他领域具有相同情形的教师获评结果进行了数据信息挖掘，挖掘结果也得到了类似情况，这就说明同一任课教师在同领域内课程的评教结果差异也不显著。

3.1.3 同一教师在不同领域内的课程评教结果差异挖掘

该部分以教授科技论文写作、过程控制工程以及现场总线与测控网络3门不同领域课程的张教师的评教结果为例，对其进行数据信息挖掘，探究同一教师由于教授课程的领域不同，是否会造成评教结果的差异(由于上文已经证明了不同班级对同一教师同一门课程的评教结果差异性小，因此可以把所有班级列为同等对象，影响评教结果差异的原因就被唯一控制为授课领域)，其数据信息挖掘结果如表4所示。

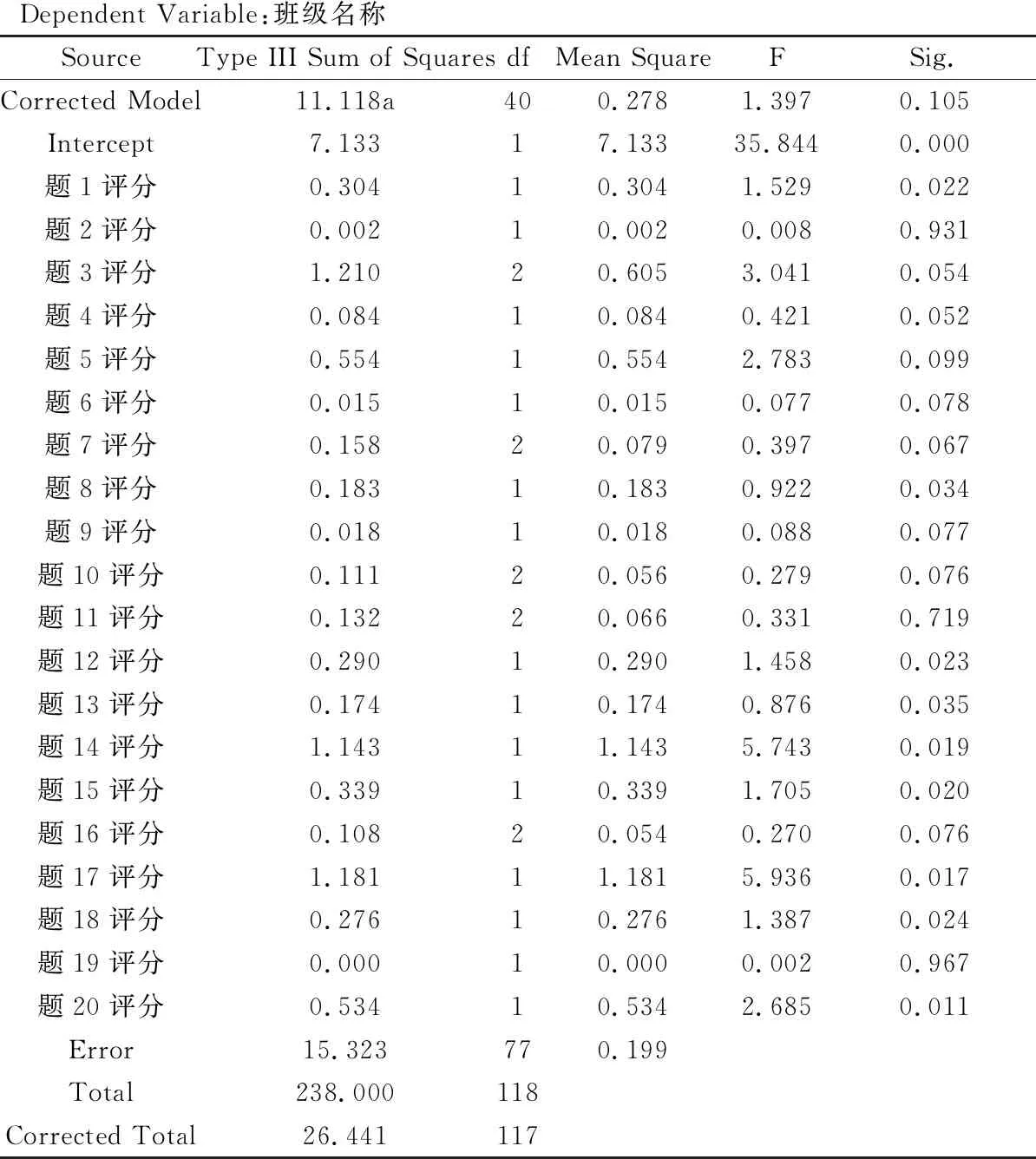
表4 方差分析(三)

a. R Squared = .420 (Adjusted R Squared = .119)

由表4的数据信息挖掘结果可以看出，评教得分在题1、8、12、13、14、15、17、18、20中存在非常显著的差异。为了验证这一结果，对其他同时教授不同领域多门课程的教师的评教结果也进行了数据挖掘，得到了类似结果。其中值得探究的是，对教授两门不同性质的必修课(动画制作)和选修课(计算机网络)的王教师的评教结果数据进行信息挖掘，结果出现了表5中的现象，从表5可以看出，所有评教题目的得分差异都非常明显。

这就说明，任课教师跨领域和跨课程性质授课，其评教结果差异性显著，可以看出，同一任课教师在跨领域、跨课程授课的情形下，所表现出的教学能力和教学水平具有争议性。

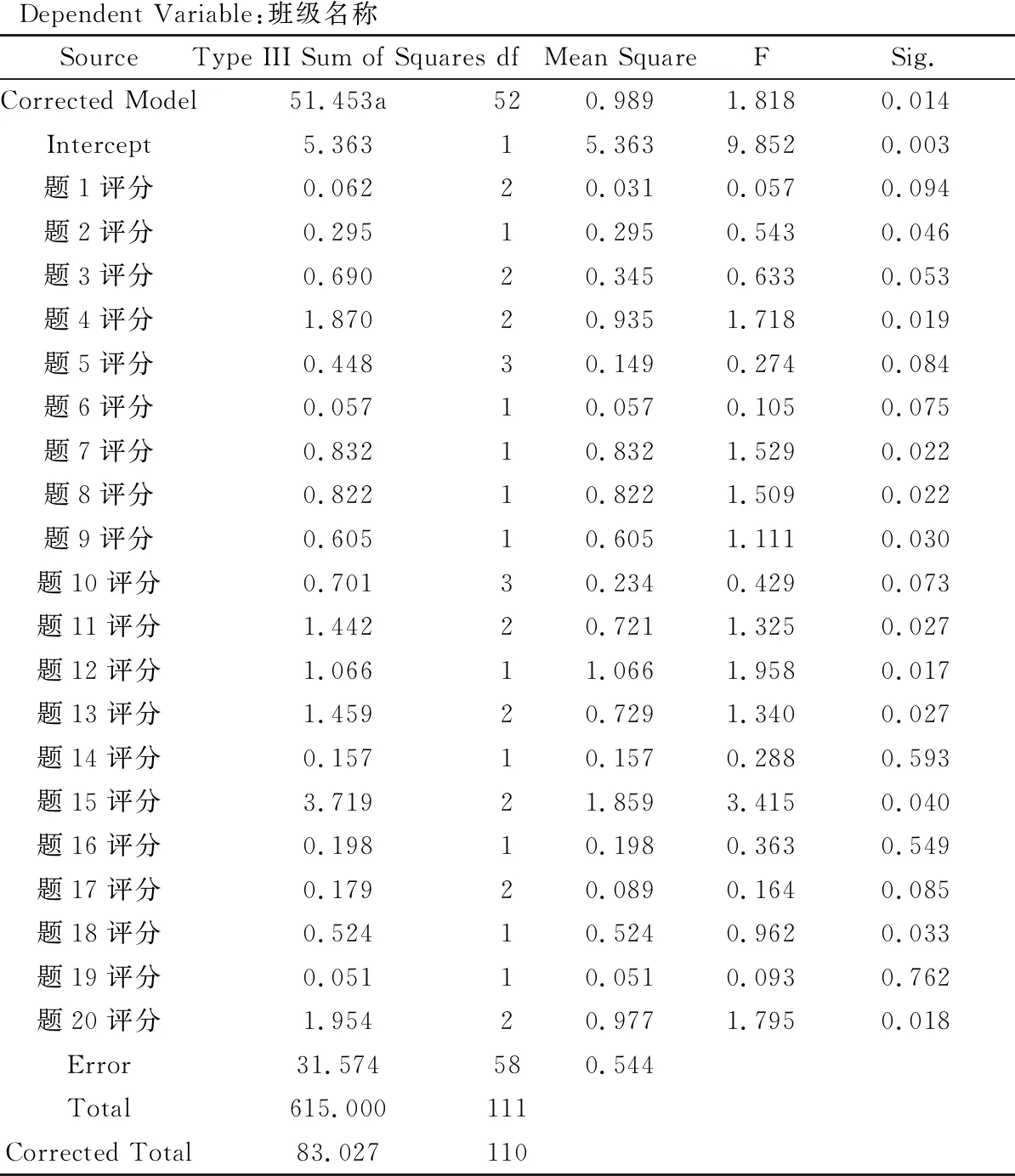
表5 方差分析(四)

a. R Squared=0.620 (Adjusted R Squared=0.279)

通过对以上3个部分评教结果进行数据挖掘分析，可以得出如下结论：

(1)不同班级对同一教师教授的同一门课程的评教结果差异性小。

(2)同一教师教授的同一领域课程的评教结果差异性小。

(3)同一教师跨领域教授的课程和教授性质不同课程的评教结果差异性显著。

通过数据信息分析可以看出，评教的班级、学生人数在评教过程中处于次要地位，其中该任课教师所开课程数量、课程的专业符合度(该门课中专业知识、视野和经验是否足够)、多开设课程的性质(必修和选修)在评教过程中处于主要地位。从而可得出，如果教师对一门课程专业知识、经验等不足，对课程(主要指选修)不重视、态度有所懈怠，很容易造成课堂教学质量的缺失和学生满意度低的现象。所以，跨领域授课的教师一定要在所授课程领域内努力提高自己的专业知识能力，增长专业知识授课经验。同时，督促选修课教师对选修课程给予一定重视，可采取灵活多变的上课手段活跃课堂氛围，同时也需任课教师摆正自己在选修课中的角色，在有限的教学设施和条件下发挥出更高的授课水平。

3.2 聚类分析法与主成分分析

根据学生评教的指标，采用聚类分析和主成分分析对评教指标进行分析讨论，从而分析出评教指标应如何设置才更具有合理性。

3.2.1 聚类分析

采用系统聚类法对20个指标进行聚类分析。由于是对变量进行分类，因此变量(问题)间的距离采用Pearson相关系数定义，首先给出相关系数矩阵表6。

表6 相关系数矩阵

采用质心聚类的欧氏距离进行分析，最终得出系统聚类树状图(见图1)。

图1 系统聚类

从图1可以看出，20个评分题目可以分为4类：①17、18、19、20题；②1、16题；③2、3、5、6、7、10、12、13、14题；④4、8、9、11、15题。

为保证分析结果的准确性，该分析方法应用了相关聚类方法。经分析比较后得出上述分类结果更具有典型性，和可信性。由此可以看到学生对评教试题是如何理解的。同时，可以看到各题之间有部分共性。考虑是否可以将试题分为几类来衡量教师教学的不同方面，以便找到教学过程的不足之处，从而进行改进，可从以下几条规则角度出发来设计调查问卷：①不设重复命题；②一题中不应有双重含义；③不应有被访人认识能力以外的命题；④放在一起易导致被调查人有倾向的命题应分开放置。

总之，应该对命题进行进一步优化组合，使命题更加互补、简洁。

3.2.2 主成分分析法

聚类分析是希望通过对学生评教数据进行分析得到学生对试题的理解，因此未对数据进行任何处理，其出发点是学生。接下来将要讨论的是评价指标设置对学生评价教师教学水平分数的影响，关注的是教师。也希望样本具有一定稳定性，因此采用的是对学生评教原始数据进行平均后的数据。

主成分分析是将多指标简化为少数综合指标的一种统计分析方法。应用主成分分析法处理数据集，在保证尽可能多地反映原始信息的基础上，用较少的互不相关的综合变量代替原来较多的分析元素，减少了维数，降低了分析难度。步骤如下：

(1)将原始数据Xm×n=(X1,X2,…,Xm)T(m表示样本，n表示分析元素) 中心标准化，消除量纲影响：

(1)

(2)由特征方程(λI-Yn×n)*μ=0，求出Yn×n各特征值λ1≥…≥λn≥0和对应的标准正交特征向量μ1,…,μn。

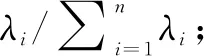
(4)通常取k使累计贡献率达到 80% 以上，研究主成分Y1,…,Yk(k

利用各主成分的方差贡献率作为其权重，计算各主成分因子的综合得分，作为样本最终评价分值。

(2)

本节讨论的是评分题目的设置对学生评价教师教学水平分数的影响。为探讨问题是否适合进行主成分分析和因子分析，首先求平均成绩的相关系数阵，并给出KMO检验和Bartlett球形检验的相关结果(见表7)。

KMO检验：用于探查变量间的偏相关性，它比较的是各变量间的简单相关和偏相关大小，取值范围在0～1之间。一般KMO统计量大于0.9时效果最佳，0.7以上尚可，0.6效果较差，小于这一限度就不适合进行因子分析了。此处KMO统计量为0.961，进行因子分析效果会很好。应用SPSS对数据进行主成分分析，结果见表8，可以看到由于各变量间高度相关，使得最终只提取出一个主成分F。

表7 KMO和Bartlett球形检验

表8 总方差解释

由于原评教数据相关系数很大，数据过于集中，因此在此基础上进行幂变换会使得数据的量纲同时增大，很难达到拉开数据距离的目的。考虑对数据进行标准化(式(1))，经过常用的Box—Cox变换和Logit变换，效果不是很理想，针对该情况观察变换前数据的公因子方差(见图2)。

图2 因子载荷矩阵与因子得分矩阵

公因子方差比指的是在提取公因子后，各评教题目(变量)中所含信息被提取出的比例，或者说原变量的方差中可以被公因子所解释的比例。可以看到，即使只提取一个主成分(公因子)，最少的第19题也被保留了原信息的84. 1%。这一结果提示，如果学生认可任课教师往往会对所有评教题目都打较高分，或者说学生在给一个教师打分时往往是凭着事先的一种印象，而不是逐题推敲最终给出评分。举例说明，如果学生在教学过程中认可这位教师，即使该教师在某方面做得不足，学生在评教时也并不会对相应的题目打出低分；同样，如果学生对某位教师不满，那么往往所有题目都会分数较低。也就是说不同题目设置在一定范围内并不会显著影响教师的最终评分。这一结果也提示评教题目完全可以设置得更加简洁。最后，根据图1中因子得分系数矩阵给出因子F1的具体形式：

F1=0.053x1+0.057x2+0.056x3+x0.054x4+x0.058x5+

0.054x6+0.058x7+0.054x8+0.056x9+0.056x10+

0.056x11+0.056x12+0.056x13+0.058x14+0.056x15+

0.052x160.054x17+0.052x180.051x19.0.052x20

(3)

对完善评教题目，分别应用聚类分析与因子分析中的主成分分析方法，结合学生评教结果对评教题目进行了统计分析。一方面，通过聚类分析方法得到了关于学生对评教题目的理解，将评教题目大致分为四大类；另一方面，通过主成分分析方法得出结论：学生通常是凭借对任课教师的主体印象给出评分，评教结果往往并不会显著受到评教题目设置的影响。

4 结论及建议

对网络评教系统中评教数据进行数据信息挖掘分析，可以得出如下结论：

(1)在课程安排方面，由于评教的班级、学生人数在评教过程中处于次要地位，而任课教师所开课程数量、课程的专业符合度、多开设课程的性质在评教过程中处于主要地位。所以应尽量使教师所教授课程数量适中，并且贴合教师的研究领域。

(2)在教学评价题目设置方面，需对命题进一步优化组合，使命题更加互补、简洁。尽量遵循以下4条原则：①不设重复命题；②一题中不应有双重含义；③不应有被访人认识能力以外的命题；④放在一起易导致被调查人有倾向的命题应分开放置。

(3)需要在教学评价题目设置尽量科学合理的情况下，综合多位学生的评价来评估教师的教学情况，以避免学生对教师的主观印象而产生的随机偏差。