绳传动型舵机反操纵负载模拟器

侯鹏飞，高 健，于 丹，王贺龙，黄海忠

(1.北京精密机电控制设备研究所，北京 100076；2.哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264209)

飞行器借助空气舵产生飞行时所需的力和力矩，舵面受空气压力作用产生对舵机的负载扭矩.当舵面压力中心处于舵机轴的前端时，气动载荷对舵机轴产生的负载力矩力图使空气舵偏转至极限位置，产生“静不稳定”的反操纵现象[1-3].为确保舵机系统的稳定性，需通过负载模拟器验证舵机的抗反操纵负载能力.

曹彤等[4-5]利用机器人平衡技术，设计出一种采用平面四杆机构的弹簧方案，王冰[6]对此进行了ANSYS和ADAMS的联合仿真；在此基础上，吴洪冲等[7]设计了4种加载梯度的机械式反操纵负载模拟器，减小了负载模拟器的体积，提高了加载精度；张小磊等[8-9]研制了基于电动加载的大扭矩反操纵负载模拟设备，解决了500 Nm扭矩、20 Hz 频宽、多余力矩抑制等技术难点；高健等[10]对某航天大功率机电伺服系统在反操纵条件下的负载特性进行了Simulink仿真分析.然而，以往研究工作不能满足大扭矩、大加载梯度、高精度的实际应用需求.

为此，本文研制了一种新型舵机反操纵负载模拟器，通过建立数学模型、动静态仿真分析及力矩标定试验，验证了负载模拟器设计的有效性.

1 方案确定

负载模拟器的设计指标参见表 1，其中Mmax为作用于舵机轴的力矩，kp为加载梯度，是加载力矩与舵偏角的比值.

表 1 设计指标

根据设计指标，本文提出两种方案：基于平面四连杆机构的曲柄-拉簧构型(简称平面四连杆型，见图 1)和基于绳传动的曲柄-压簧构型(简称绳传动型，见图 2).

图 1 平面四连杆型Fig.1 Four-bar linkage configuration

平面四连杆型方案通过拉簧作用于摇杆末端实现对舵机轴的反操纵力矩加载，利用伺服电机驱动丝杠调节滑块的移动量，以满足不同加载梯度的加载要求.绳传动型方案通过控制伺服电机调节滑块的移动量，使得压簧积蓄的弹力经由牵拉绳传动作用于曲柄，实现对舵机轴的反操纵力矩加载.

图 2 绳传动型Fig.2 Rope-drive configuration

经分析，绳传动型在传动效率、可靠性、动态特性、安装方便性等方面具有显著优势，且不存在平面四连杆型的死点问题，两种设计方案对比参见表 2.因此，本文选择绳传动型方案作进一步研究.

表 2 两种方案对比

2 数学建模

绳传动型方案中，牵拉绳一端固定于曲柄末端，另一端连接于压簧自由端.当给定某一加载梯度后，首先伺服电机动作以调节压簧的初始变形量，通过力传感器反馈值加以控制.曲柄摆动时，压簧自动调整其变形量，实时调节牵拉绳上的作用力，从而获得作用于舵机轴的反操纵力矩.负载模拟器数学模型如图 3 所示.牵拉绳选用凯芙拉绳，主要承受压簧作用于绳端的拉力，弯曲载荷对其影响极小，同时忽略牵拉绳伸长形变、挠度、绳与滚轮间摩擦力及其它非线性因素的影响.

图 3 负载模拟器数学模型Fig.3 Mathematical model of load simulator

对负载模拟器受力分析可知，曲柄作用于舵机轴的反操纵力矩为

M=Fh=(KSΔx)h,

(1)

式中：F为牵拉绳的受拉载荷；KS为压簧弹性系数；Δx为压簧变形量.存在以下几何关系

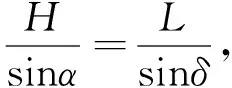
(2)

h=rsinα,

(3)

(4)

Δx=x0-(r+H-L).

(5)

综上可知，反操纵力矩M的表达式为

M=f(δ)=

式中：x0为δ=0°时对应的压簧变形量；舵偏角δ满足

3 详细设计

负载模拟器包括伺服电机、齿轮减速器、联轴器、丝杠、滑块、压簧、牵拉绳、滚轮、力传感器、曲柄及台体等部分，篇幅有限，本文仅介绍压簧和伺服电机的设计思路.

3.1 压簧

根据式(6)，当曲柄处于最大摆角时，计算不同加载梯度下压簧承受的载荷峰值，结果如表3所示.根据承载要求，本文设计了两种不同刚度的压簧A和压簧B，其中刚度较小的压簧B备用，详见后文.

表 3 压簧载荷峰值

压簧刚度KS及试验切应力峰值τmax为

(7)

式中：G为材料切变模量，取G=79 GPa；Fmax为压簧承受的载荷峰值；K为曲度系数，K=(4C-1)/(4C-4)+0.615/C,C为旋绕比，C=D/d.

经计算，压簧A，B的刚度分别为275 N/mm和154 N/mm，二者试验切应力峰值均小于许用切应力([τ]=740 MPa)，满足使用要求.

3.2 伺服电机

当负载模拟器对舵机轴进行静态加载或低频(≤5 Hz)正弦加载时，曲柄为大幅低速摆动，要求伺服电机动作以实时调节压簧的变形量.取舵机轴摆动频率为5 Hz，经ADAMS运动学分析可知：滑块的理论移动速度峰值为104 mm/s，要求伺服电机的理论转速峰值为 4 992 r/min；滑块的理论移动加速度峰值为2 974 mm/s2，要求伺服电机的理论角加速度峰值为14 949 rad/s2.

据此，初选伺服电机的设计参数，并计算电机的角加速度设计峰值为

式中：Td max为伺服电机最大输出转矩；JD,JZ,JM分别为伺服电机的平动负载(含滑块、压簧、丝杠螺母等)惯量、转动负载(含丝杠轴、联轴器、齿轮减速器等)惯量、转子惯量.综上分析，伺服电机满足使用要求.

4 仿真分析

4.1 静态加载分析

当曲柄摆动至某一角度后，根据式(8)计算不同梯度下牵拉绳上的初始作用力.当伺服电机驱动滑块调节到位后，保持滑块固定不动，负载模拟器静态加载误差参见式(9).取中间值kp=75 Nm/°，绘制静态加载力矩曲线和静态加载误差曲线分别如图 4，图 5 所示.

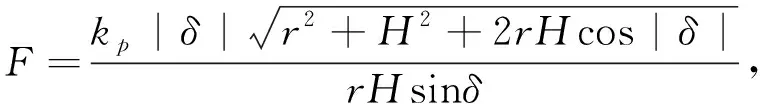
(8)

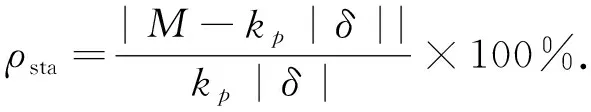
(9)

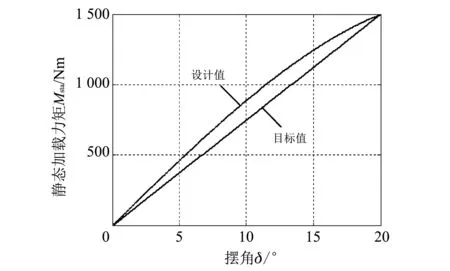
图 4 静态加载力矩曲线Fig.4 Curves of static load torque

图 5 静态加载误差曲线(滑块固定)Fig.5 Curve of static load error (slider’s fixed)

由图 5 可知，曲柄摆角越小，负载模拟器的静态加载误差越大，最高达23.30%.对于负载模拟器的静态加载或低频(≤5 Hz)正弦加载，可控制伺服电机使滑块实时随动，以实现力矩的高精度跟踪.滑块随动原理为：当曲柄摆动时，压簧产生了变形量ΔL，其间伺服电机应驱动滑块移动ΔL，使作用力F趋于定值，以补偿该过程中的力矩变化.采用滑块随动形式后，静态加载误差曲线如图 6 所示，此时最大误差仅0.51%.表 4 给出了不同加载梯度下静态加载误差峰值，可见相比于滑块固定，滑块随动状态的加载精度有了显著改善，可满足静态加载要求.

图 6 静态加载误差曲线(滑块随动)Fig.6 Curve of static load error (slider follows)

加载梯度/(Nm/°)静态加载误差峰值/%滑块固定滑块随动3560.900.675540.820.677523.300.511156.950.22

4.2 动态加载分析

动态加载是指舵机轴在偏置条件下，叠加正弦形式摆动.当负载模拟器对舵机轴进行高频(>5 Hz)正弦加载时，曲柄为小幅高速摆动，在测试时保持滑块固定不动，压簧随着曲柄摆动自动调整其变形量，实现高频力矩的动态加载.本文针对幅值2°的工况要求，对负载模拟器的动态加载情况进行分析.取中间值kp=75 Nm/°，曲柄摆角依次取最大舵偏角的100%, 80%, 60%, 40%, 20%，绘制动态加载力矩曲线和动态加载误差曲线分别如图 7，图 8 所示.

图 7 动态加载力矩曲线Fig.7 Curves of dynamic load torque

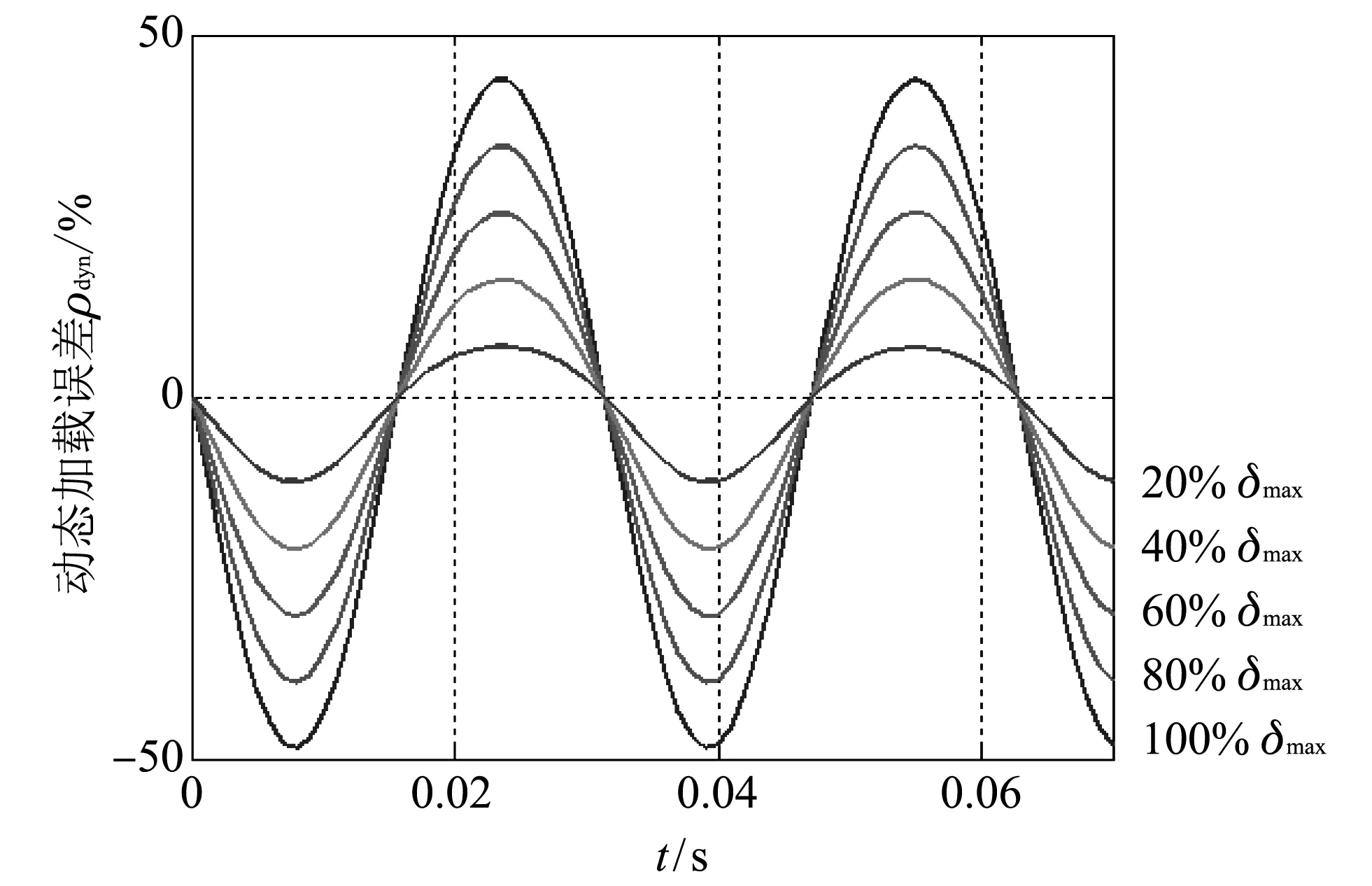
图 8 动态加载误差曲线Fig.8 Curves of dynamic load error

由图 8 可知，曲柄摆角越大，负载模拟器的动态加载误差越大，最高达4.85%.对于压簧A和压簧B，不同加载梯度下的动态加载误差峰值参见表 5.可见，加载梯度越小，加载误差峰值越大；当加载梯度为35 Nm/°和55 Nm/°时，宜选用刚度相对较低的压簧B，以满足动态加载指标.

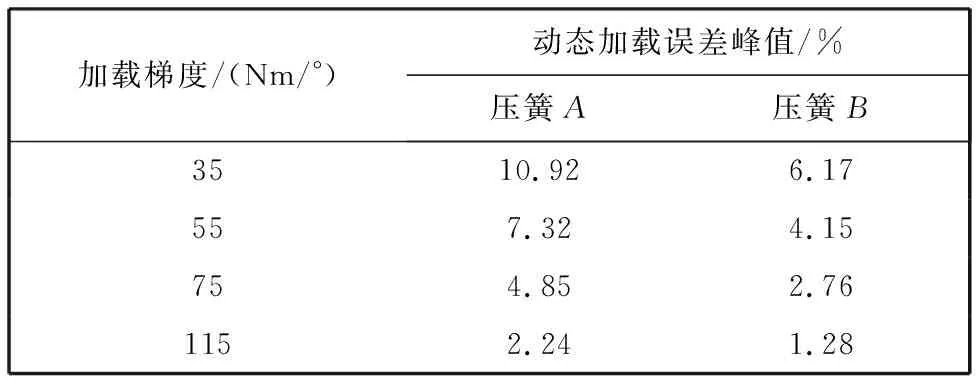
表 5 动态加载误差峰值结果

仿真分析中，假定压簧刚度为常值，不考虑压簧的阻尼特性，认为压簧能够无相位差地跟踪目标力矩.实际上，压簧的非线性与自身材料特性、加工误差、热处理状态及使用环境等相关，在此不作分析.

5 力矩标定试验

负载模拟器工作时，力传感器实时采集水平作用力FN(见图 3)，存在几何关系式(10)，由此得到施加于曲柄的反操纵力矩M.式(11)中忽略了负载模拟器刚性、摩擦及其它非线性因素的影响，在正式测试前应对反操纵力矩进行标定.

(10)

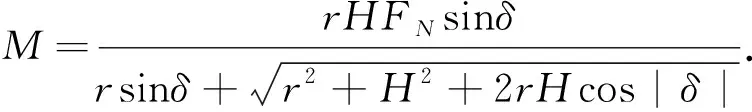
(11)

力矩标定试验系统如图 9 所示，包括调整盘、力矩传感器、联轴器、编码器及负载模拟器本体等部分.首先，操纵调整盘使曲柄摆动至某一角度，通过编码器精确读取曲柄摆角值.通过负载模拟器对曲柄加载，利用力传感器测量水平力FN，计算理论反操纵力矩M，同时记录力矩传感器实测值M′.在指标范围内选取一组工况点进行测试，采用最小二乘法处理试验结果得到：M′=1.017 8M+2.732 2.由表 6 中部分工况点数据可知，理论力矩与力矩传感器测值的偏差小于3%，满足加载要求；经最小二乘法修正后，加载力矩偏差控制在1%以内，大大改善了加载精度.

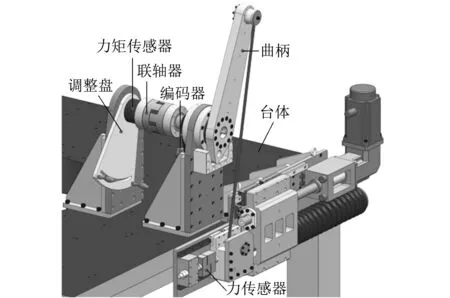
图 9 力矩标定试验系统Fig.9 Test system of torque calibration

力矩传感器测值/Nm曲柄摆角/°理论力矩/Nm修正前力矩偏差/%修正后力矩偏差/%240.8015.23235.212.320.55318.4020.22310.102.610.02474.0010.55463.472.220.09604.0015.45593.051.810.38748.4010.71727.702.770.67984.0015.68958.402.600.601 089.620.681 074.71.360.63

6 结 论

1) 基于绳传动的曲柄-压簧构型方案首次被提出并应用于反操纵负载模拟试验中，相比于传统平面四连杆型方案，其具有传动效率高、可靠性高、动态响应快、无工作死点、安装方便等优势.

2) 对于静态加载，滑块固定状态的加载误差峰值最高达60.90%，滑块随动状态的加载误差峰值则不大于0.67%，静态加载精度得到显著改善.

3) 对于动态加载，曲柄摆角越大，负载模拟器的加载误差越大；当加载梯度较小时，如本文中选取的35 Nm/°和55 Nm/°，宜选用刚度相对较低的压簧，以提高动态加载精度.

4) 为提高实际加载精度，应开展力矩标定试验，经最小二乘法修正后，加载力矩偏差可控制在1%以内.