一种全景相机系统的标定方法研究
2019-07-23崔红霞李婷婷陈丽君
崔红霞,李婷婷,王 宁,陈丽君
(渤海大学 信息科学与技术学院,辽宁 锦州 121000)
0 引 言
全景相机[1-3]是近年来摄影测量学和计算机视觉等领域研究的热点,多用于虚拟现实、智能交通、文物保护、影视拍摄等领域。一般地,全景相机由多个相机组成,以获取不同视角影像,是实现三维场景高精度快速重建的手段之一[4-6]。全景相机的标定内容包括确定相机的内方位元素(像主点、主距和畸变参数)以及相机的外方位元素[7]和相机间固定的相对定向关系。传统的标定方法是在同一参考坐标系下对每台相机的内外方位元素分别标定,再利用外参数间接解算相机间的相对约束关系。这一类方法操作简单方便,但没有利用到相机之间的相对定向关系。文献[8-9]以立体相机为研究对象,利用激光扫描技术对相机进行标定并提高三维重建结果的精度,但没有利用相机间的约束条件;文献[10-12]以立体相机为研究对象,有约束条件限制,按照附有约束条件的间接平差模型进行自检校光束法整体平差解算,有效地增加平差系统的多余观测数,提高标定的精度和稳健性;文献[13-16]以全景相机为研究对象,利用基于二次曲线、线性矩阵的奇异值、圆形标志点等方法对全景相机的各组成相机进行单机标定,再解算相机间的相对定向关系,实验结果显示,标定方法可行、有效,具有较高的标定精度。文中建立了一种附加约束条件的全景相机标定方法,即以共线条件方程为基础,将相机间内在的几何约束引入到自检校光束法平差模型,以实现一种全景相机系统的标定。
1 全景相机系统的标定
文中采用的全景相机由八个处于同一平面的网络摄像机构成,通过同步曝光的方式进行影像采集。标定场由分布在四个平面的800多块标志板组成。如图1(a)所示,固定在八边形底座支架上,根据均匀分布原则在不同方位安装摄像机,保证了周围360°水平空间及至少60°垂直方向的视觉信息获取无遗漏。图1(b)为全景相机的俯视图,分别为1-8号摄像机。

图1 全景相机
1.1 传统的相机检校方法
相机检校通常使用的方法有单像空间后方交会、自检校光束法区域网平差等。其数学模型为带有畸变方程的共线方程式,如下:
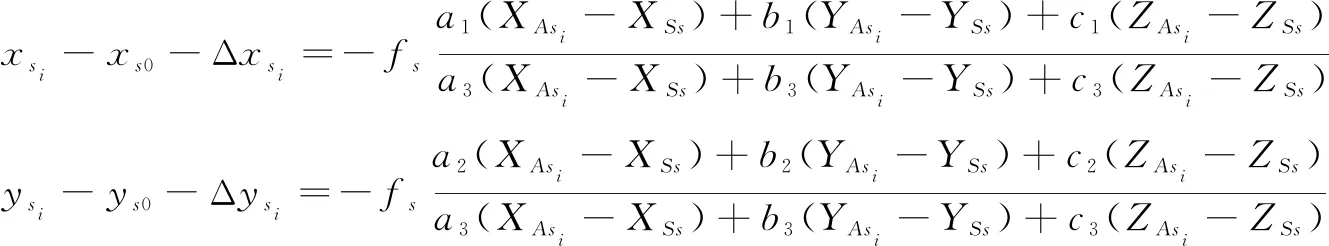
(1)
其中
其中,s(s=1,2,…,8)为相机编号;(xsi,ysi)为s号相机像点的像平面坐标,其中i=1,2,…,n;xs0、ys0、fs为相机影像的内方位元素;(XSS,YSS,ZSS)为摄站点的物方空间坐标;(XAsi,YAsi,ZAsi)为相机物方点的物方空间坐标;aj、bj、cj(j=1,2,3)为影像的3个外方位角元素组成的9个方向余弦;Δxsi和Δysi分别表示相机影像的x,y方向的畸变误差;k1s、k2s为影像径向畸变参数,p1s、p2s为影像切向畸变参数,b1s、b2s为影像仿射畸变参数。
式1中共线方程的观测值与未知数之间是非线性函数,需要对其进行线性化,用一阶泰勒级数公式展开,再求得各相机相应元素改正数的系数,得到共线方程线性化公式如下:
c11ΔXSs+c12ΔYSs+c13ΔZSs+c14Δφs+c15Δωs+c16Δκs-c11ΔXsi-c12ΔYsi-c13ΔZsi+c17Δxs0+
c18Δys0+c19Δfs+c31Δk1s+c32Δk2s+c33Δp1s+c34Δp2s+c35Δb1s+c36Δb2s-lxs=0
c21ΔXSs+c22ΔYSs+c23ΔZSs+c24Δφs+c25Δωs+c26Δκs-c21ΔXsi-c22ΔYsi-c23ΔZsi+c27Δxs0+
c28Δys0+c29Δfs+c41Δk1s+c42Δk2s+c43Δp1s+c44Δp2s-lys=0
(2)
其中,c11,c12,…,c44为相应的偏导数系数;ΔXSS、ΔYSS、ΔZSS、ΔφS、ΔωS、ΔκS、ΔXsi、ΔYsi、ΔZsi、Δxs0、Δys0、Δfs、Δk1s、Δk2s、Δp1s、Δp2s、Δb1s、Δb2s为每台相机相应元素改正数。
1.2 附有约束条件的全景相机检校方法
在传统的单相机检校的自检校光束法平差模型的基础上,文中引入相机间约束条件即相对定向关系[17],建立了附有约束条件的全景相机自检校光束法平差方法。以相邻相机m、n(m=1,2,…,7;n=2,3,…,8)为例,相机间的相对定向约束条件如下:
(3)
(4)
其中
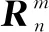
考虑到全景相机系统中各个摄像机都是紧固相连的,可以假定相机之间的相对位置姿态是稳定的。利用全景相机在不同时刻拍摄若干组影像,则p时刻和q时刻相邻相机m和n之间存在如下约束关系:
(5)
(6)
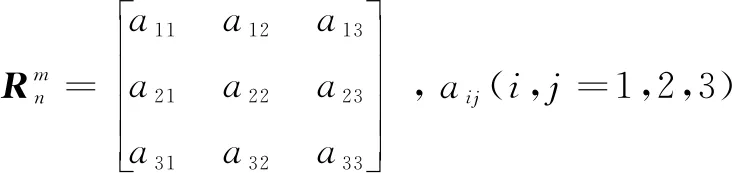
结合式5和式6,考虑到式5中旋转矩阵的正交性,以主对角线以下的三个元素为例是相互独立的[11-12]。
具体约束方程为:
(7)
(8)
(9)
(10)
需要对约束方程线性化,按一阶泰勒级数公式将式7展开得到的线性化公式,如式11。
即:
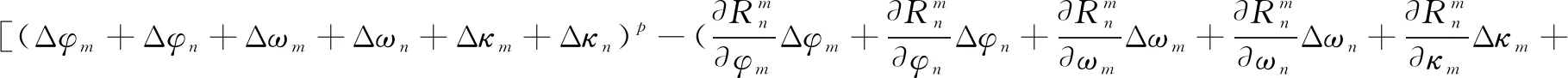
(11)
式8和式9方法相同,再将式10展开,如下:
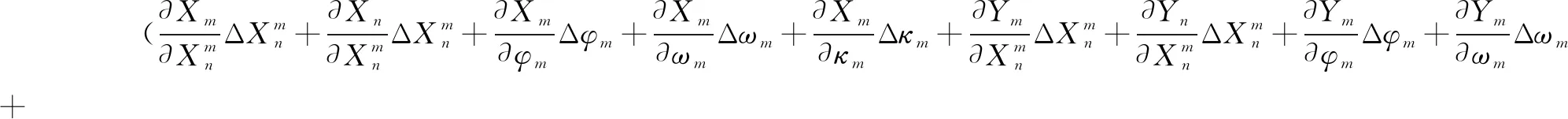
(12)
文中探讨的全景相机标定方法,所采用的全景相机是由8个网络摄像机组合而成,所涉及到的约束条件有7组,每相邻两相机之间的相对定向关系都是不变的。以1.1节的传统相机检校误差方程与相机间相对定向约束条件的误差方程[18-20]相结合,构建附有约束条件的全景相机的自检校光束法误差方程,其中方程2写成矩阵形式,如式13所示,式7~式10写成矩阵的形式,如式14所示。
VS=A1X1+A2X2+A3X3-L1
(13)
CX3-L2=0
(14)
式13、式14组成附有约束条件的间接平差模型。其中,VS为观测数的改正值;X1为相机内方位元素改正值;X2为相机自身畸变参数改正值;X3为相机外方位元素的改正值;L1、L2为误差方程的常数项(其中i,j,…,p为每台相机的像点号),m、n为相邻相机(m=1,2,…,7;n=2,3,…,8);A1、A2、A3、C分别为所对应项的系数矩阵。根据式13、式14构建其对应的附有约束条件的间接平差法方程,如下:
(15)
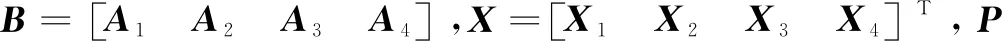
(16)
解算过程中,为提高鲁棒性,利用验后定权迭代法进行迭代求解,并且迭代过程剔除残差大于2倍中误差的观测值;最后,利用任意时刻相邻相机获取的像对的外方位元素,根据式3、式4计算其相对定向元素,即可反算出任意相邻相机的位置和姿态[10-12]。
2 实验分析
文中所采用的实验检校场为三维标定场,由800余个标志板组成,实验对象为8个网络摄像头组成的全景相机,摄像机焦距约为4 mm,获取的影像大小均为2 048 pixel×1 920 pixel,拍摄距离约为2 600 mm,标志板为70 mm×70 mm的标志物,实验场中分别对每块标志板进行数字编号,并以高精度全站仪测定所有控制点的三维空间坐标。对于第i(1,2,…,8)个子相机的第j幅影像(j=1,2,3,4),首先人工量测4-6个控制点,使其均匀分布于影像,以直接线性变换计算初始外方位元素,用于控制点反投影计算;利用初始的外方位元素以共线方程计算初始像点坐标以确定椭圆的区域;从起始点进行8邻域跟踪确定椭圆边界;基于最小二乘椭圆拟合的方法提取椭圆中心点坐标作为控制点精确的像点坐标并对其编码(如图2所示,1号相机在同一摄站获取的不同角度影像的像点提取和编码)。图2是以1号相机为例在不同角度拍摄的检校场的局部图。

图2 不同角度拍摄的检校场的局部图
将全景相机在不同摄站、不同姿态获取的实验场影像组合成6组影像,前3组影像,采用了三个摄站,每个相机在各摄站仅有四个姿态的影像;后3组影像,每个摄站8个姿态的影像;利用各组影像包含的标志点的空间坐标和像点坐标,完成传统方法和文中方法的检校实验。
2.1 检校结果分析
设方法A是传统独立相机的检校方法,方法B是采用了相机间的固定相对定向关系的检校方法;以相机1、2、3为例,分别以两种方法解算相邻相机的相对定向参数(位置、姿态),每相邻两相机之间的相对定向参数如表1和表2所示。
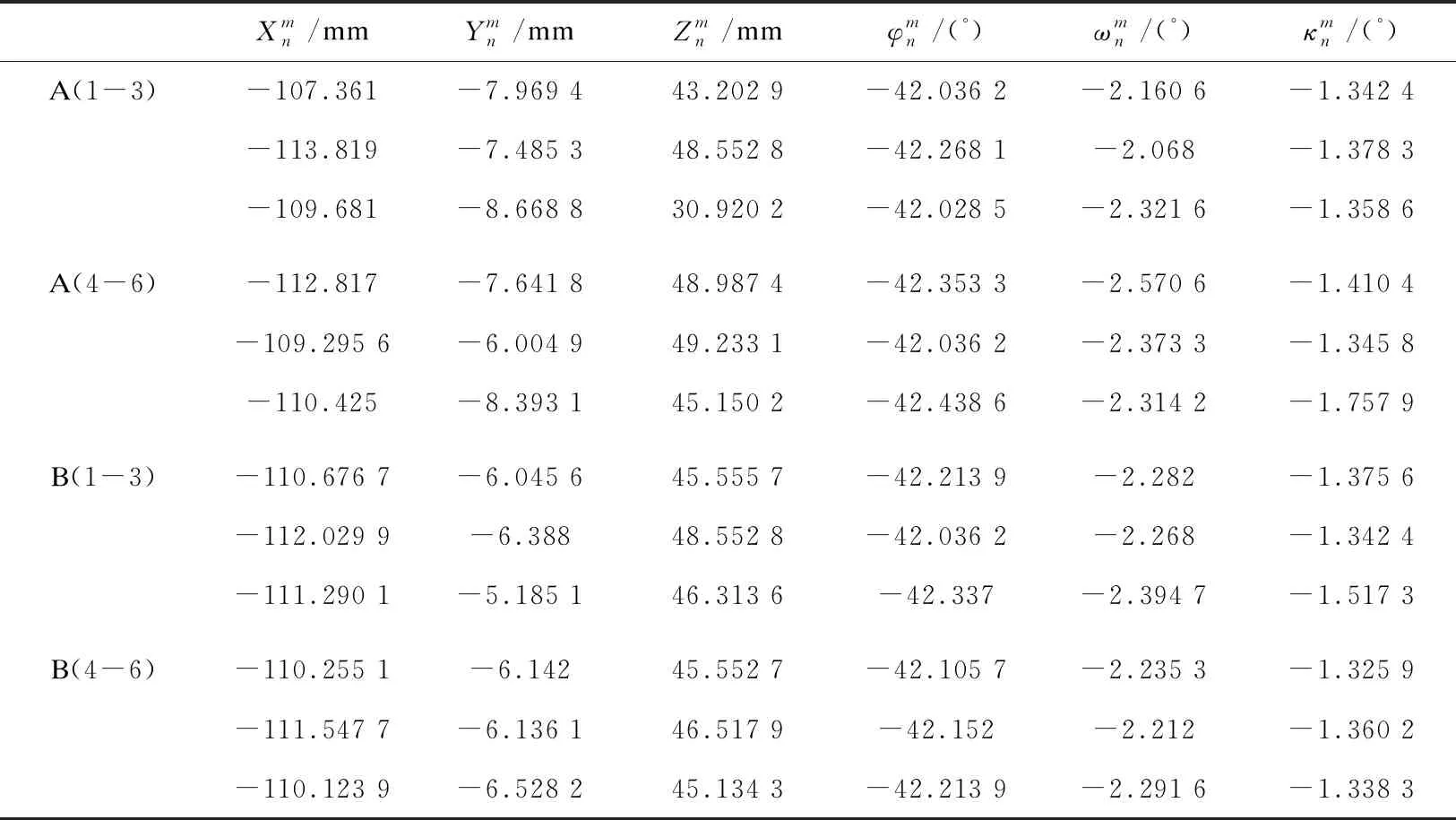
表1 相机1、2的相对定向参数比较
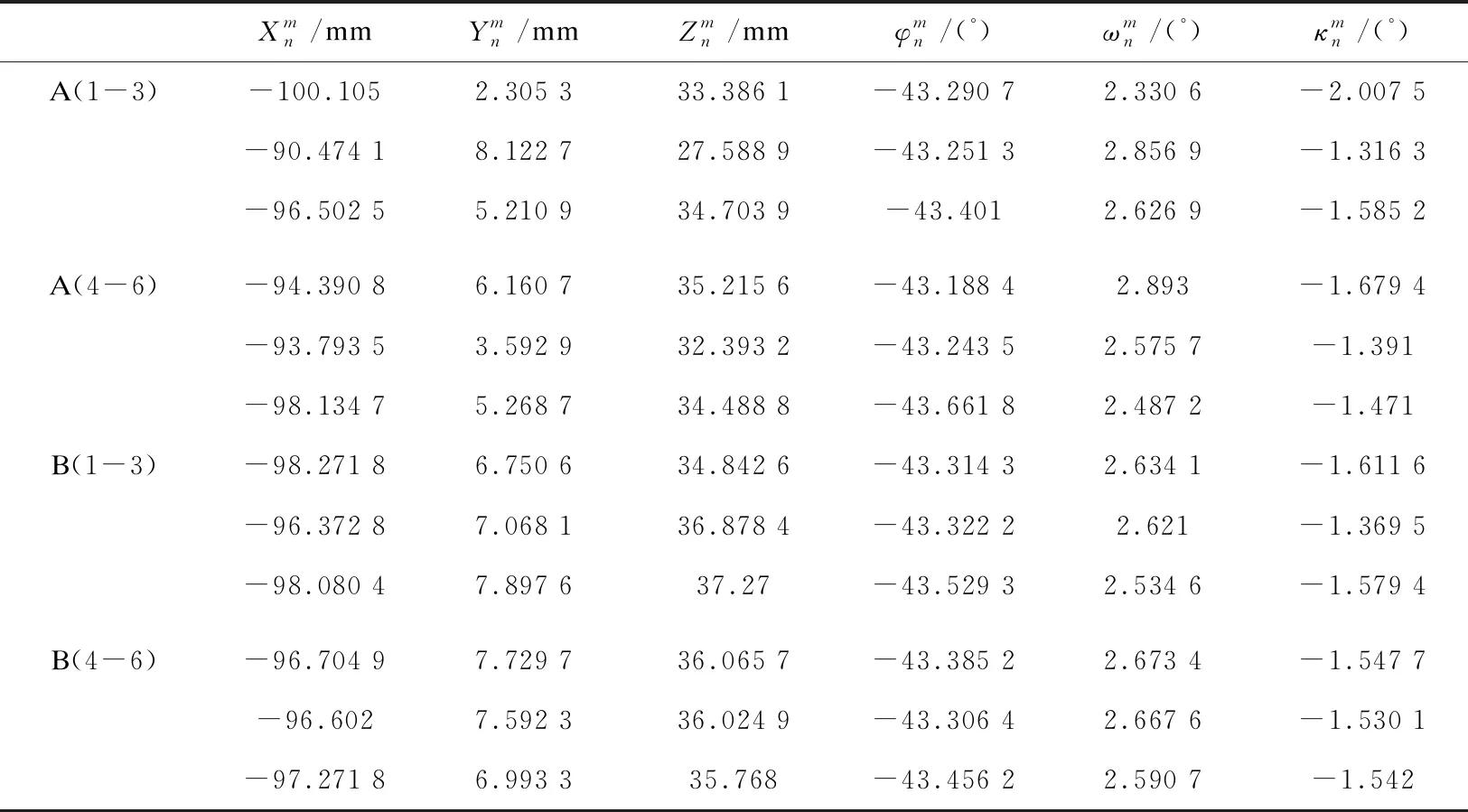
表2 相机2、3的相对定向参数比较
由表1、表2可以看出,利用方法A(传统方法)检校单个相机再计算相机之间相对定向关系)的前3组相对定向参数波动很大,其原因在于外方位线元素和角元素之间存在很大的相关性,内外方位元素以及畸变参数之间存在很大的相关性,其检校的稳健性和精度受影像的姿态、摄站的布置、控制点的分布和数量等复杂因素的复合影响较大,因此导致整个检校结果的波动大[1,11,14,16];方法B因引入了固定的相对定向约束条件有利于克服参数之间的相关性,前3组数据的波动性低于方法A,但还是存在波动。后3组数据,因增加了每个摄站的影像数(不同姿态),方法A的检校结果也能趋于稳定,其8个子相机之间内部两两相机的相对定向三个方向的线元素的最大标准差(单位:mm)分别为2.352、2.474、2.619,最小标准差分别为1.230、1.391、1.465;内部各两两相机之相对定向角元素的最大标准差分别为0.212、0.134、0.221,最小标准差分别为0.05、0.04、0.01。方法B三个方向线元素的最大标准差分别为1.031、0.513、0.693,最小标准差分别为0.108、0.007、0.026;相对定向角元素的最大标准差分别为0.006、0.028、0.008,最小标准差分别为5.06×10-4、7.43×10-5、8.06×10-5。方法B的内部相对定向关系波动更小、可以忽略不记,更趋于稳定。
2.2 检校精度分析
标定场共有809个均匀分布的标志点,选择其中分布均匀的112个作为检查点,其余为控制点。利用方法B的检校结果,统计检查点在8个独立相机影像上的反投影像点中误差和检查点在X、Y和Z方向上的坐标中误差,如表3所示。

表3 相机检查点误差统计
从表3可以看出,基于文中检校方法,7个相机的反投影像点平面中误差均控制在0.81 μm以内,即小于1/3 pixel(像元尺寸为2.5 μm),其中4号相机的反投影误差大于1/3 pixel小于1/2 pixel。检查点物方空间坐标误差在X方向和Y方向比Z方向小,X方向的误差在2 mm以内、Y方向的误差在1 mm以内、Z方向误差控制在2.5 mm内;考虑到摄影距离2 600 mm,平面方向的相对精度达到1/1 858,深度方向(Z方向)的相对精度约为1/1 253。但个别检查点本身误差较大,测量精度不高,尤其在深度方向的精度较差。
3 结束语
传统两个或两个以上相机组成的系统标定沿用单相机检校方法,方法简单,但容易出现相机之间的相对定向计算结果不一致的稳健性问题;对于多个相机组成的全景相机,各相机之间的相对定向关系标定的不一致,直接影响全景虚拟拼接成像的精度和稳定性,甚至无法全景虚拟成像。文中拓展单相机和立体相机检校方法,提出了一种附有约束条件的全景相机标定方法。多个网络摄像头构建的全景相机系统的标定实验证明,引入相对定向关系的标定方法能取得稳健的标定结果且检校精度较高,可推广至其他类似的全景相机系统的标定。为进一步提高测量精度,需要进一步分析控制点的数量、分布、控制点测量精度对全景相机检校精度的影响;进一步分析摄站的设置对检校精度的影响,研究相邻相机相对定向角元素和线元素约束条件的定权方法以提高检校精度。
