一种电液伺服控制器的设计及Matlab仿真

姚坤杉，王 直

(江苏科技大学，江苏 镇江 212000)

0 引 言

目前电液伺服控制系统在各行各业中有着广泛的应用，尤其在高精度，大功率控制系统中，如船舶、飞机等领域，因此电液伺服系统的控制品质有着越来越高的要求[1-2]。

将32位浮点型DSP STM32F103ZET6和ST公司的ARM芯片TMS320F28335结合使用，充分发挥软硬件结合的优势，拓展控制器的功能，同时提高系统的稳定性和控制精度。在现代工业中，PID控制因为其良好的控制精度和较高的稳定性而被广泛采用，而对于参数不确定的系统，常规PID的控制效果不太理想[3-4]。电液伺服系统参数具有不确定性，因此将模糊控制与PID控制相结合，根据电液伺服系统参数的实时变化，自动调整PID控制的参数，能够达到更好的控制效果。针对电液伺服系统控制问题,文中对电液伺服系统进行建模，通过matlab/simulink仿真比较，证明模糊PID控制比常规PID控制具有更强的适用性和更好的控制效果。

1 系统总体设计

1.1 液压控制系统的工作原理

电液伺服系统的核心是电液伺服阀，它将接收的模拟信号转换为油缸的流量与压力输出[5]，电液伺服控制系统的结构框图如图1所示。

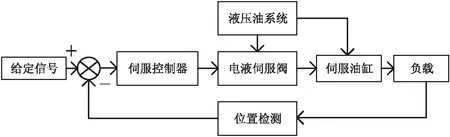
图1 控制系统硬件结构框图

1.2 伺服系统的数学模型

为使系统动态特性分析与设计得到简化，电液伺服阀二阶近似传递函数如下:

(1)

其中，Q(S)、I(S)分别为在S域中伺服阀流量和控制电流的表示；KQ为伺服阀的流量系数；ξQ为伺服阀的阻尼比；WQ为时间常数。

液压缸的传递函数由两部分组成：进油腔的流量连续方程和活塞运动方程。液压缸进油腔的瞬态流量连续方程为：

(2)

活塞运动动力平衡方程为：

(3)

其中，A为液压缸进油腔活塞面积；v为活塞的运动速度；λ为液压缸的泄露系数；K为油液体积弹性模量；V为液压缸高压腔及进油管路油液体积；m为活塞及负载折算质量；B为黏性阻尼系数；F为活塞所受压力[6]。由此可得液压缸的传递函数为：

(4)

其中，Wh为液压固有频率；ξh为液压阻尼比。

位移传感器的输入信号为液压缸活塞杆的位置信号，输出为电压信号，频宽比系统的频宽高得多，因此可视为比例环节[7]。设Ka为伺服阀放大增益,Kf为反馈增益，可以得到被控对象的开环传递函数为：

(5)

2 硬件系统设计

系统硬件采用STM32F103ZET6(以下简称STM32)和TMS320F28335(以下简称DSP)，STM32主要功能为：控制外围电路、A/D转换、D/A转换、硬件自检测、故障报警；DSP主要功能为：算法计算、CAN通信。两块芯片通过SPI通信传递各种变量和参数。同时配置了显示模块用于实时监控系统的运行情况，在线设定控制参数。控制系统的硬件机构如图2所示。

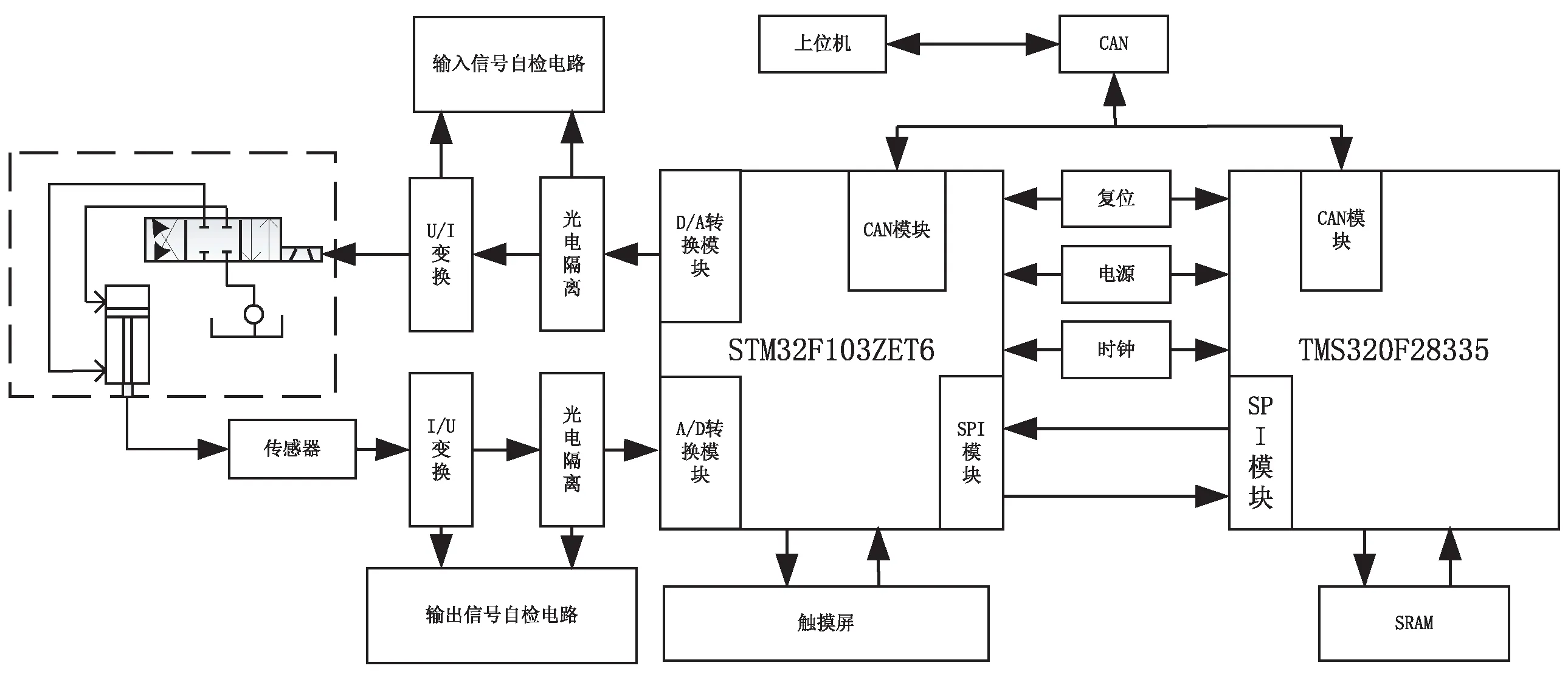
图2 控制系统硬件结构框图

3 软件设计

3.1 模糊自整定PID控制

模糊自整定控制就是运用模糊数学的基本理论和方法，制定模糊规则储存在计算机中形成知识库，在计算机运行过程中，根据输入量调用知识库中的模糊规则，调整输出量，从而使系统达到最佳的控制效果[8-10]。

模糊自整定PID控制器通过模糊参数调整器调用知识库中的模糊规则，调整输出量传递给变参数PID控制器，变参数PID控制器的输出与被控对象的输入连接[11-12]。在文中设计的模糊自整定PID控制中，模糊参数调整器的输入为系统误差E和误差变化率EC，输出为控制量的增量，即PID参数的增量。模糊参数调整器根据输入的误差以及计算得出的误差变化率，调用知识库中的模糊规则，调整输出比例系数Kp，积分系数Ki和微分系数Kd的增量ΔKp、ΔKi和ΔKd，输出的增量与初始参数相加再传递给变参数PID控制器。结构如图3所示。

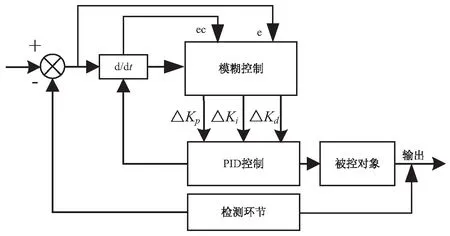
图3 模糊PID控制结构

3.2 建立模糊规则

PID参数的整定要综合考虑Kp、Ki和Kd在不同时刻对系统的影响以及相互之间的联系[13-14]。系统在运行中不断检测E和EC的大小,然后根据制定的模糊控制规则调整输出量[15]。比例系数Kp的作用在于加快调节速度，还可以减小稳态误差，但是Kp的值过大会引起超调量的上升，增加振荡次数，使动态性能变差[16]；积分系数Ki可以消除稳态误差，提高控制精度，但Ki的值过大会引起积分饱和产生较大的超调；微分系数Kd影响系统的动态品质，抑制偏差，但Kd的值过大会延长调节时间，降低系统的抗干扰能力[17]。综上，归纳出自调整规则如下：

(1)当误差E的值较大时，此时可忽略误差变化率的趋势[18]，Kp和Kd的值取大一些，提高系统的响应速度；同时为避免系统响应出现较大超调，应取较小的Ki值。

(2)当误差E的值为中等大小时，Kp的值应取适中大小，防止超调[19]。Ki和Kd也应取适中大小的值，避免系统响应速度太慢。

(3)当误差E的值较小时，Kp取较小的值避免超调；Ki的值应取适中，提高系统的稳态性能。此时还应兼顾系统的抗干扰能力和避免系统振荡，当EC较小时，Kd取较大一点的值；当EC较大时，Kd应取较小一点的值[20]。

定义E、EC模糊量的论域为{-3,3}，模糊子集为{NB，NM，NS，Z，PS，PM，PB}；ΔKp、ΔKi、ΔKd模糊量的论域为{-3,3}，模糊子集为{NB，NM，NS，Z，PS，PM，PB}；子集中元素分别代表负大，负中，负小，零，正小，正中，正大。ΔKp、ΔKi、ΔKd在论域上的输出曲面如图4(a)、(b)、(c)所示。

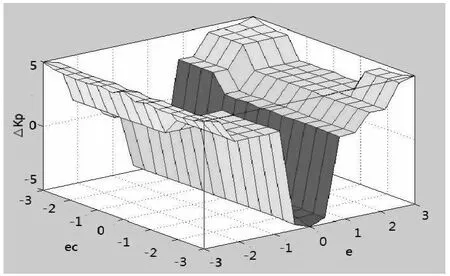
(a)ΔKp

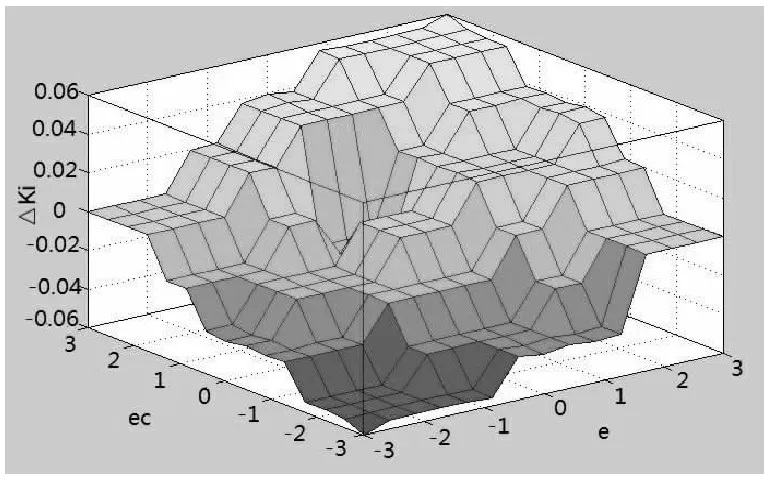
(b)ΔKi

(c)ΔKd图4 输出曲面

3.3 控制系统的软件流程

系统上电初始化后，STM32首先执行电路自检故障程序，确认外围电路无故障后，通过A/D转换模块将输入信号传给STM32，DSP通过DPI通信接收A/D转换模块传递给STM32的数据，并通过算法的计算将计算后的数据回传给STM32，STM32通过D/A转换将从DSP接受的数据转换为模拟信号输出给伺服阀，可以通过触摸屏查询DSP中算法的参数，以及查看输出量，偏差量，偏差变化率。系统流程如图5所示。

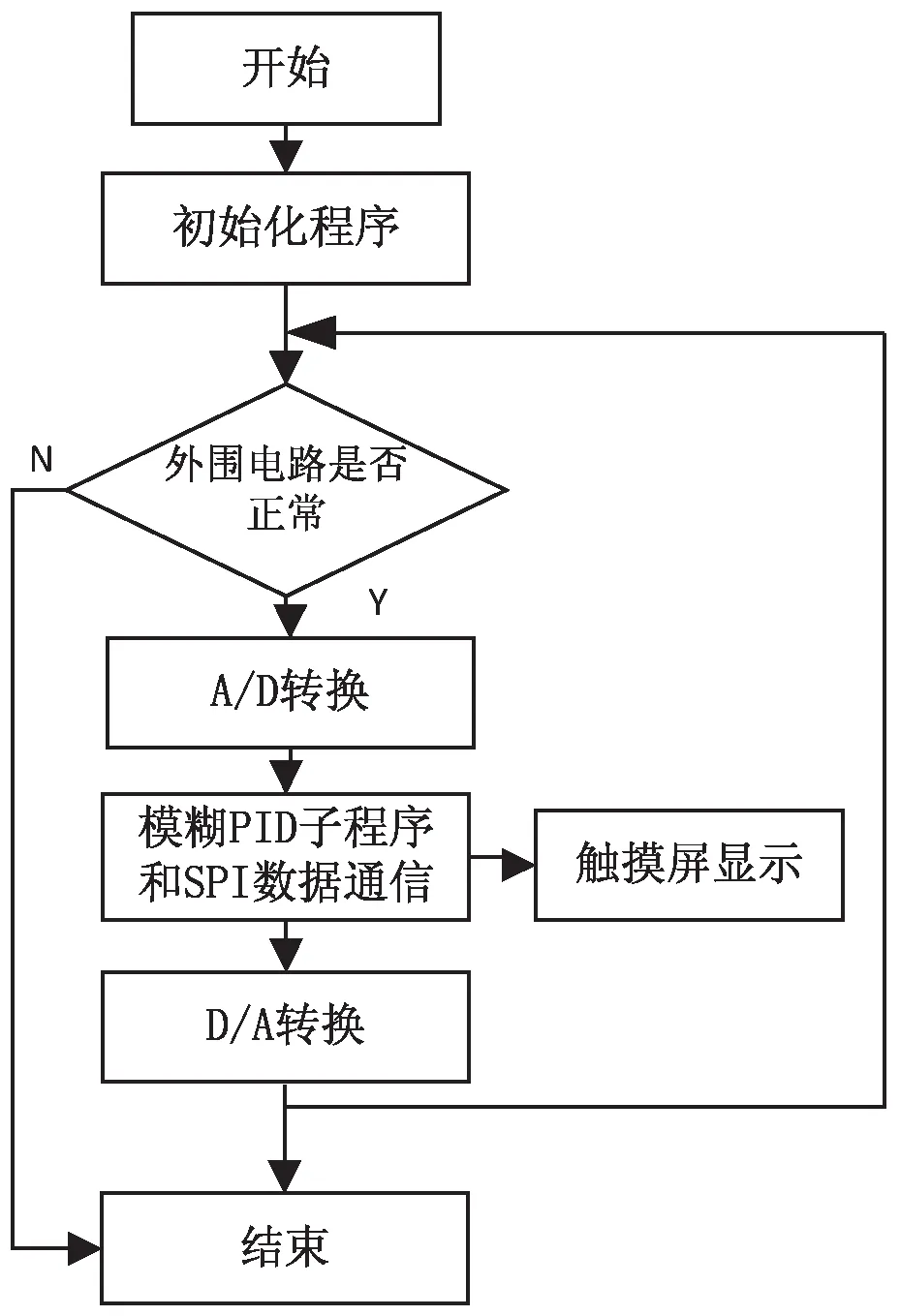
图5 主程序流程

3.4 Matlab建模

利用Matlab提供的Simulink工具箱对系统进行建模，仿真和分析。将伺服系统的系数带入式5，得到被控对象的传递函数为：

G=5/[S(2.61×1011S4+1.96×108S3+

1.54×105S2+6.20×103S+1)]

根据图3在Matlab的Simulink环境下设计系统的仿真框图，模型如图6所示。

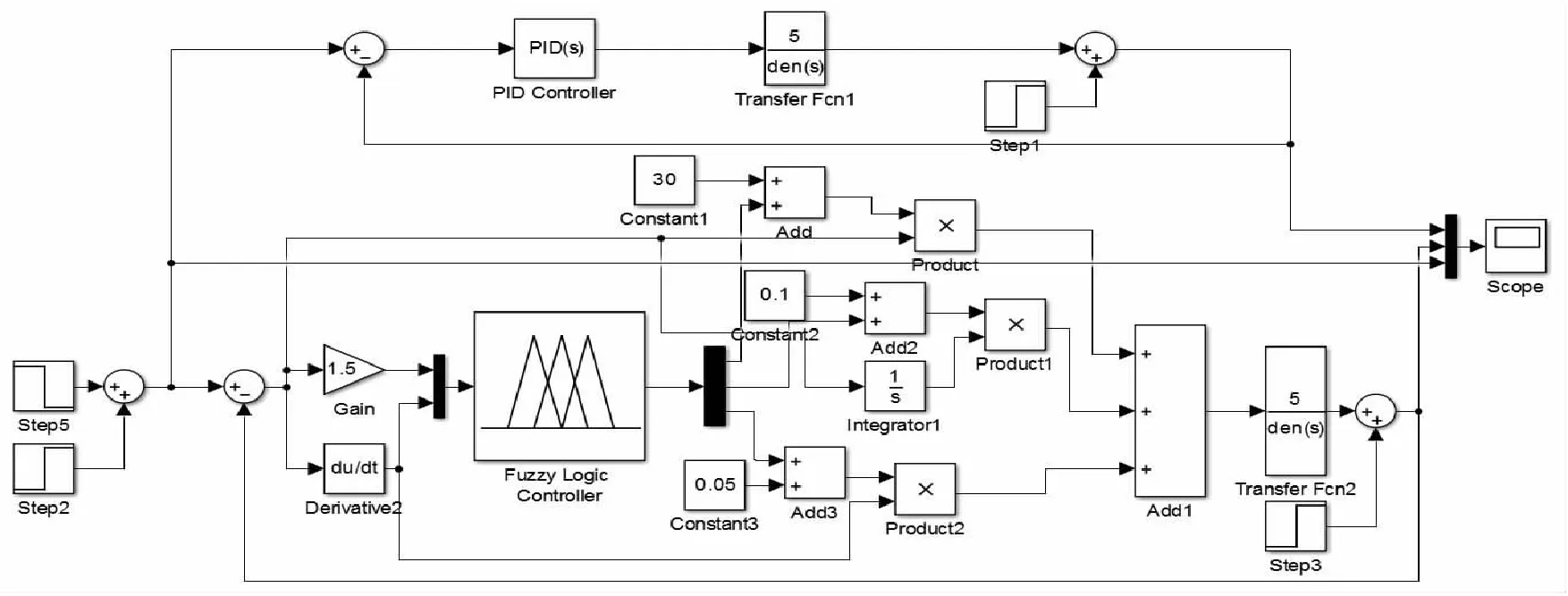
图6 电液伺服系统Simulink仿真框图

3.5 仿真结果分析

在Simulink中对电液伺服系统进行仿真，得到系统的仿真曲线如图7所示。从仿真图可以看出，采用模糊PID控制时系统的超调量减小了一半，同时系统的调节时间也变小；在0.08 s时，输入信号突变，模糊PID控制比常规PID控制响应更快，调整时间更短。这表明模糊PID控制比常规PID控制具有更强的适用性和更好的控制效果。

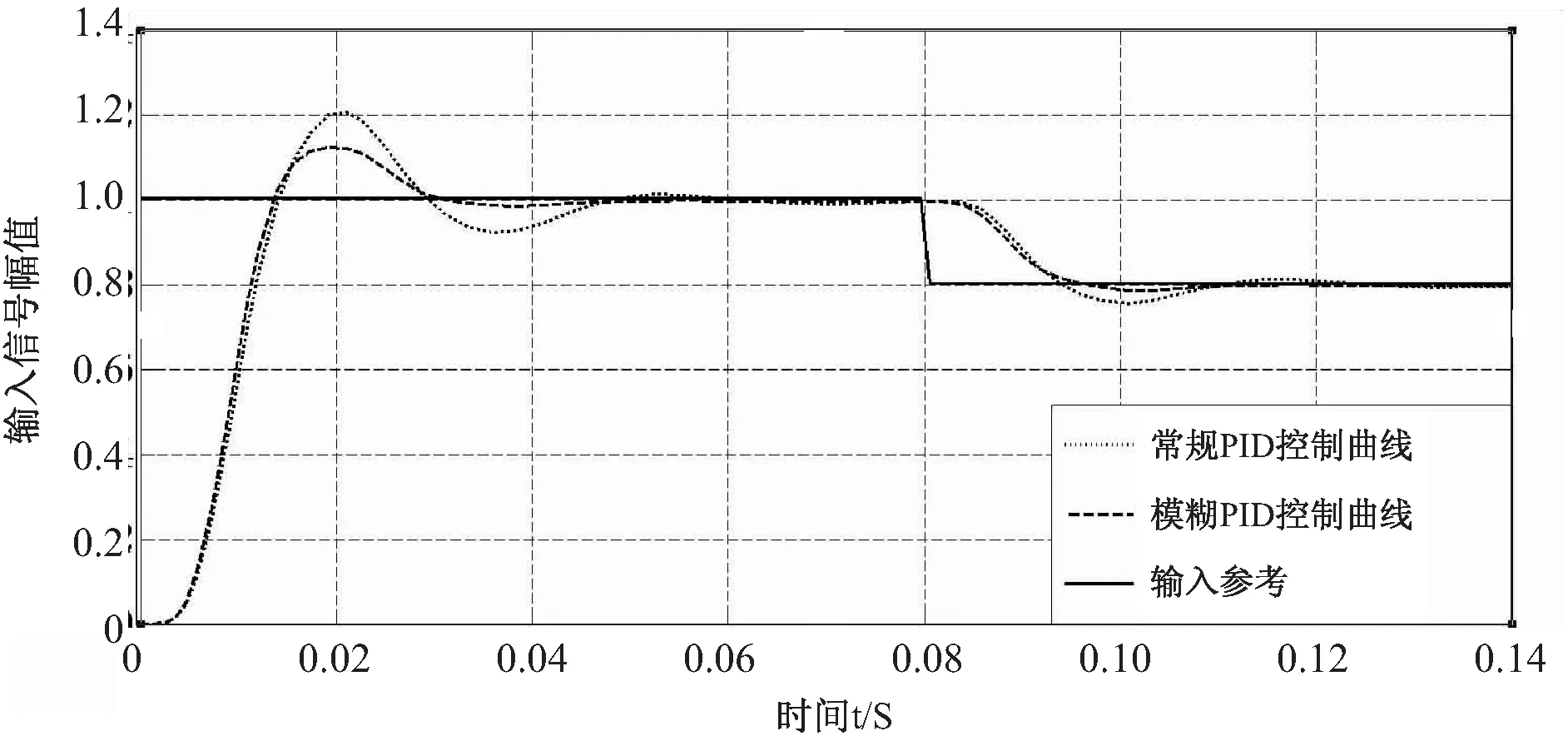
图7 常规PID控制和模糊PID控制曲线图

4 结束语

采用32位浮点型DSP STM32F103ZET6和ST公司的ARM芯片TMS320F28335双核心处理器，通过SPI通信分工协作，充分利用了单片机的控制优势和DSP的数据处理功能进行高精度电液伺服控制。模糊PID控制是建立在PID控制基础上的，根据工况变化过程中偏差E和偏差变化率EC，通过模糊推理自动调整PID参数Kp、Ki和Kd的值，两种控制方式相结合能够取长补短。从仿真结果可以看出，自整定模糊PID控制器改善了电液位置伺服系统的稳态和动态性能，提高了工作精度，而且结构简单实用，具有一定的通用性。