基于KPCA初始化卷积神经网络的方法
2019-07-23蔡楠,李萍
蔡 楠,李 萍
(宁夏大学 物理与电子电气工程学院,宁夏 银川 750021)
0 引 言
卷积神经网络(convolution neural network,CNN),属于人工神经网络的一种[1],相对于传统的识别算法不需要将输入的数据进行特征提取和数据重建,而直接可以将图像作为网络的输入,自动提取特征并且对图像具有高度不变性。其权值共享的网络结构显著降低了模型的复杂度,减少了权值的数量,是目前语音分析和图像识别领域研究的热点[2]。网络参数的训练与更新是CNN的关键环节,占用了大量的运算资源和时间,并且为了获得足够的拟合精度,通常需要大量的有标签样本来进行训练[3]。
卷积神经网络一般由输入层、卷积层、池化层、全连接层、输出层组成,其中卷积层的可训练权值被称为卷积核。卷积神经网络的初始化是针对卷积核及全连接层的权重值进行合理有效的初始化,使网络降低训练难度,更快收敛[4]。
在初始化方法中最为常见的是随机初始化,其主要方法是通过选取某种概率分布生成一组随机数来初始化卷积核[5]。该方法十分简单且易于操作,但是存在较大的偶然性和不确定性,导致网络的不稳定性大大增加。在2010年,由Glorot等提出了Xavier算法初始化CNN,由于一般的神经网络在前向传播时神经元输出值的方差会不断增大,而利用Xavier算法理论上可以保证每层神经元输入输出方差一致[6-7],但是Xavier算法从本质上讲还是通过生成随机数来完成初始化,因此网络仍然存在着不稳定性。文献[8]中通过主成分分析(principal component analysis,PCA)对每个卷积层输入的每幅图像先进行所有感受野的采集,然后通过PCA提取主成分将其作为网络的权重,从而达到初始化网络权重的目的。该方法解决了通过随机数初始化网络带来的不稳定性,同时避免了人工设定超参数,但是由于PCA在提取非线性特征上能力较差,无法提取图像中存在的非线性特征,不能更加有效地初始化网络权重。为此,文中提出了一种基于核主成分分析(kernel principal component analysis,KPCA)的方法来初始化卷积神经网络的权重,称为KPCA-CNN。KPCA-CNN通过对每个卷积层输入的每幅图像的所有感受野进行取样作为KPCA的输入样本,经KPCA映射至高维特征空间提取出所有感受野的非线性特征作为网络权重的初始值,以提高网络的准确率,加快网络的收敛速度。
1 卷积神经网络
1.1 基本结构
一般卷积神经网络由输入层、卷积层、池化层(下采样层)、全连接层、输出层构成,如图1所示[9]。
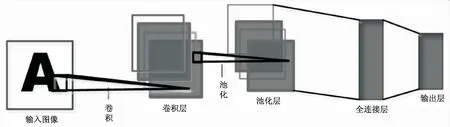
图1 卷积神经网络模型
与传统的神经网络相比,CNN主要增加了两层:卷积层与池化层。其中卷积层是由输入图像与卷积核通过卷积后所得到的特征图,通过卷积运算使输入图像特征增强,降低噪声干扰,从而更好地提取图像特征[10]。池化层一般在卷积层之后,主要目的是通过池化操作将卷积层中的特征图进行特征降维,减少网络的计算量。将经过多个卷积层与池化层后的特征图通过全连接层完成对图像的分类和识别[11]。具体过程如下:
假设卷积神经网络第i层的输入图像为Xi(输入层的图像为X0),Ci表示第i个卷积层,Si表示Ci之后的池化层,Hi表示第i个卷积层中的特征图,Ji表示Si中池化后的特征图。
生成Hi的过程如下:
Hi=f(wi*Xi+bi)
(1)
其中,wi表示第i个卷积层中的卷积核;“*”表示卷积运算符;bi表示第i个卷积层中的偏置项;f(·)表示非线性激励函数。
之后通过池化层(Si)所得特征图Ji如下式所示:
Ji=subsampling(Hi)
(2)
其中,subsampling表示池化操作。
最后由全连接层根据卷积层与池化层所提取特征进行图像分类与识别。
1.2 卷积神经网络初始化
卷积神经网络在训练过程中通过反向传播使损失函数达到最小,最终收敛于某个值,而有效的初始化,能减少网络的训练复杂度和迭代次数,因此卷积神经网络初始化就是更好地为各个卷积层的卷积核,全连接层的权值,各层的偏置项进行初始化,由于池化层采用固定结构所以无需初始化。KPCA-CNN主要针对卷积核的初始化,全连接层的权值采取随机数初始化,卷积层的偏置项均设为0。
2 KPCA初始化卷积核
2.1 KPCA原理
核方法是解决非线性模式分析问题的一种有效途径,核心思想在于通过某种线性的映射将原始数据映射到合适的高维空间,再通过线性的学习器在新的高维空间中分析处理模式[12-13]。
核函数如下所示:
k=<φ(xi),φ(xj)>
(3)
其中,“<·>”表示内积运算符;φ为原样本向高维特征空间的映射。
KPCA是PCA的一种非线性改进,主要是将样本经非线性变换映射至高维特征空间[14-15],在高维特征空间中使原样本线性可分,从而更好地提取非线性特征。
设一组样本集X={X1,X2,…,Xn},其中n为样本个数,KPCA原理如下:
(1)将样本映射至高维特征空间φ(X);
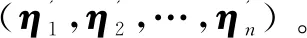
2.2 KPCA初始化卷积核的方法
以网络中第一个卷积层为例,具体算法过程描述如下:
假设输入层有2幅图像,第一个卷积层中有4个卷积核,卷积核的大小为3×3。
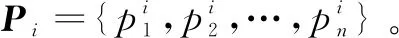
(3)把所提取的主成分作为卷积核的初始值,对卷积神经网络的卷积核w1、w2、w3、w4进行初始化。
3 实验仿真
实验1:采用Python中sklearn自带的数据库生成100个半月形分布数据,如图2所示,分别经PCA与KPCA进行处理,结果如图3和图4所示。从图3和图4中可以看出,经PCA处理的数据不能有效地将非线性分布的数据完全分开,而KPCA能够有效地使非线性分布数据完全分开,从而能更加有效地提取非线性特征。
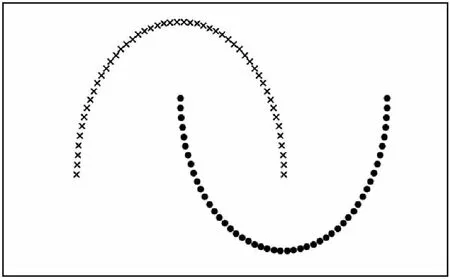
图2 生成的半月形分布数据
图3 经PCA处理后的数据
实验2:使用Python语言,通过TensorFlow搭建卷积神经网络,其结构为:输入层,3个卷积层,3个池化层(均采用最大池化方式),感受野大小均为2×2,1个全连接层,包含625个神经元,输出层包含了10个神经元;卷积核大小为3×3,个数分别为:32,64,128。分别用PCA初始化方法和KPCA-CNN,在MNIST手写数字识别上进行100次训练,结果如图5所示。
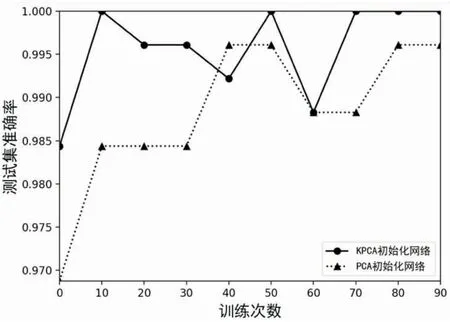
图5 准确率
由图5可以看出,KPCA-CNN比PCA初始化CNN在测试集上的准确率整体高出许多。KPCA初始化网络训练约70次就可以达到收敛,而PCA初始化网络训练约80次才能达到收敛。
4 结束语
针对卷积神经网络中卷积核初始化的问题,提出了一种基于KPCA的初始化方法。实验1的结果说明了KPCA比PCA有更好的非线性特征提取能力。实验2用KPCA和PCA两种初始化CNN的方法在MNIST数据集上进行训练,由于KPCA提取了原图像中大量的非线性特征来初始化卷积核,从而增加了网络识别准确率,加快了网络的收敛速度,从而表明KPCA能更有效地初始化卷积神经网络。
