基于多目标约束遗传算法的SDN路径增强算法
2019-07-23何利文唐澄澄侯小宇陆钱春
周 睿,何利文,唐澄澄,侯小宇,陆钱春
(1.南京邮电大学,江苏 南京 210003;2.中兴通讯股份有限公司,江苏 南京 210012)
1 概 述
网络的稳定性是网络正常运行的重要前提,减少网络变更对生产生活的影响就变得至关重要,这同时还会减少相关设备和协议的巨大安装成本。想在传统网络上有所创新变得困难,几乎没有什么办法来尝试新的网络协议,因此人们普遍认为网络设施已经变得僵化了[1]。但是随着移动设备和内容的爆炸式增长、服务器虚拟化,以及云计算的出现推动了网络的进一步发展,行业开始重新审视传统的网络架构。传统网络结构是分层的,由分布式排列的交换机和路由器构成,这种设计在客户机-服务器计算时是占主导地位的,但是这样的静态架构不适合今天的企业数据中心、校园网、运营商环境的计算和存储需求[2]。近年来,SDN(software defined networking,软件定义网络)的提出,为目前出现的这些网络问题找到了新的方向。不同于传统的网络,SDN控制器将网络设备的数据平面和控制平面分离,使用一个集中的控制器来决定网络中所有转发组件的行为[3]。并且为相关的网络应用提供可编程的接口,利用软件的方式对整个网络的资源进行控制,革命性地改变了现有的网络架构[4]。
在传统的网络体系架构中,路由协议改进非常困难,这主要是由于设备更新换代以及网络自身的复杂性比较高,同时也会带来非常巨大的开销等[5]。传统的QoS体系结构(基于分布式控制平面)被证明是过于静态的,无法获得更广泛的应用[6]。SDN的出现直接降低了新型网络开发的成本,其倡导控制转发分离、网络能力接口的开放、软硬件解耦和网络功能的虚拟化,这将会推动网络架构向软件化、集约化、智能化和开放化的目标网络架构演进[7]。
它的关键技术包括控制和转发解耦、实现控制集中化和网络能力开放化这几个方面,一个SDN控制器可以对转发平面多台设备进行通信,同时提供了一系列的开放编程接口,这样对网络业务的加载和控制更加灵活[8]。以往的路由算法通常是由分布式实现,即交换机需要生成并维护转发表,实现对网络的集中配置与管理,而在SDN网络中,数据转发由控制器集中管理[9],因此,只需要通过控制器来设计与数据转发有关的程序。在具有全局的网络状态和应用需求的情况下,可以在一个集中的系统中执行得更高效[10],SDN控制器的出现大大简化了路由创新的门槛。
网络资源的中心化让以前的分布式算法控制路由转发成了历史,这也是造成网络低效的原因之一。现在通过中心控制器可以高效地管理数据转发,让网络流量更加可控,可以直接使用Dijkstra算法[11]来计算最短路,达到最佳路由。然而,SDN控制器支持的最短路径算法无法较好地部署三层路由技术,还有就是Dijkstra算法的时间复杂度并不低,随着网络结点的增加,CPU的消耗越来越高,网络寻址的效率也会降低。SDN现在最常见的应用是在IDC网络中,这种网络通常会有成千上万个网络节点,因此,提出一种效率更高的算法是极具意义的。与此同时,网络服务提供商需要根据客户的SLA(服务等级协议)为其定制特定级别的高质量网络服务,即需要满足如带宽、时延、严格下一跳等等条件[12]。Qos需求路由问题可以理解为寻找满足多个约束条件的可行路径问题,这是属于NP难问题,通常无法在多项式时间内求解[13]。所以文中采用基于启发式算法的遗传算法来解决这个问题。
遗传算法(genetic algorithm,GA)是由J.H.Holland等于20世纪70年代提出并发展起来的[14],也是启发式算法的一种,还是一种具有全局搜索能力的直接、并行、随机的优化方法。它通过模仿生物的进化,遵循进化的主要原则,本质上是先通过随机方式选出初始种群,根据特定的评定标准,通过选择、交叉、变异的遗传算子的优化作用,优选出性能最佳的一系列个体[15]。因为遗传算法具有很强的全局寻优能力和适应性,被广泛地应用于路径规划问题。所以这里采用多目标约束遗传算法解决多约束路由问题,既能一次计算产生多条可选路径路由,也可以根据业务的需求动态调整路由计算的参数,来得到所需要的路径。
文中提出的遗传算法是在已有物理拓扑状态下根据具体的业务标准需求的多目标约束遗传算法,可以在并行的情况下自适应地计算出符合路径约束条件的若干条可用路径,保证每个业务都有充足的备用路径可供调整。对该算法的主要思想和流程进行了介绍,然后对算法展开了详细描述,最后对算法在给定的网络环境下的性能进行了分析,验证该算法对SDN路径增强问题的有效性。
2 SDN网络约束
2.1 网络模型及问题描述
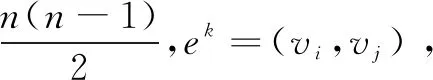
即如果两节点之间有链路连通,则矩阵对应的元素为1,否则为0。同理,链路带宽容量矩阵用B={bi,j},vi,vj∈V,ek=(vi,vj)∈E表示,其中bi,j表示节点i和节点j之间链路的带宽容量大小;时延矩阵D={dij},vi,vj∈V,ek=(vi,vj)∈E,dij表示节点i和节点j之间的链路时延的值,cij表示节点i和节点j之间的链路开销的值。
2.2 约束优化模型
假定两个节点vi,vj之间有一条不带环的通路路径,记为:path=(vi,vj),如果路径path经过链路ek,那么ek∈path,否则ek∉path。文中路径是由染色体个体的形式表示的,即每个染色体代表一条路径,有x1,x2,…,xn,这里使用变长的实数编码的方式,以s和d为其起始节点,每个个体所表示的路径经过的节点数量是不定的。多约束路由问题中的多约束条件可以表述为:
(1)
(2)
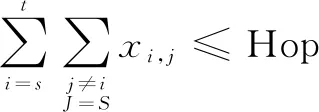
(3)
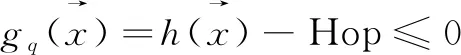
(4)
∀(xij=1)bi,j·xi,j>BandWidth

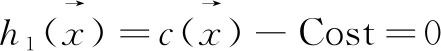
(5)
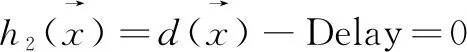
(6)
其中,xij表示路径x中对应的链路有效因子,当(vi,vj)属于x时,xij=1,否则xij=0。Cost、Delay、Hop、Bandwidth分别是SDN路由中要求的额定开销、时延、跳数和带宽的可变参数,在这里一般表示为常数。
3 改进的多目标约束的遗传算法
3.1 路径编码
根据网络拓扑路径的特点,采用链式变长实数编码的方式,如:源节点是0.0,目的节点是120.3,路径依次经过节点0.0、3.5、50.9、70,3、62.8、109.5、120.4,那么路径编码就是0.0→50.9→70.3→62.8→109.5→120.4。这样的编码和解码的过程相对来讲比较简单,代表每一个节点的实数根据网络中节点的数量会做相应的调整,随着网络规模的变化相应地改变小数位的位数,如图1所示。
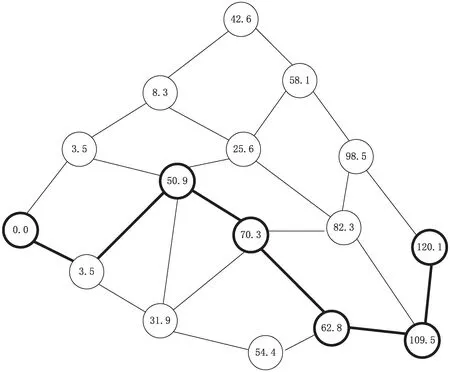
图1 网络拓扑
3.2 种群初始化
遗传算法需要通过初始种群的生成的筛选满足路径规划类约束条件。这里引入了He L在用混合遗传算法解决电信网络备用路由的研究中提出的SPA算法(最短路径优先)[16],并且根据约束条件进行改进,在原有随机路径选择生成的过程中满足相应的约束条件。算法流程如下:
(1)从源节点开始;
(2)寻找所有与源节点相连接的节点,记录这些节点作为当前节点;
(3)检查这些当前节点中是否有目的节点;
(4)如果有,则记录源节点和目的节点之间的链路,计算完成,否则,继续计算;
(5)继续查找与当前节点相连的节点,作为当前节点;
(6)查看这些节点是否有源节点,如果有则将其从列表中删除;
(7)重复步骤3,直到找到最短路径为止。
约束条件为:严格下一跳和松散下一跳;排除某个节点;亲和力属性的处理。
改进的SPA算法:
(1)从源节点开始;
(2)寻找所有与源节点相连接的节点,记录这些节点为当前节点集合;
(3)检查当前节点是否有目的节点;
(4)如果有,则记录源节点和目的节点之间的链路,计算完成,否则继续计算;
(5)检查当前节点中有无需要排除的节点,如果有则从当前节点中删除,继续计算;
(6)检查当前节点集合中有无严格下一跳或者松散下一跳的节点,如果集合中有下一跳节点就走上去,否则继续计算;
(7)检查与当前节点集合中节点连接的所有链路上的亲和力属性有无满足当前业务的亲和力属性,如果有就走该链路,否则继续计算;
(8)继续查找与当前节点相连的节点,作为当前节点;
(9)查看这些节点是否有源节点,如果有则将其从列表中删除;
(10)重复步骤3,直到找到可行的路径为止。
3.3 个体选择
个体选择概率取决于种群中个体的适应度及其分布,为了简单有效地控制选择压力并且使得个体有更好的鲁棒性,选择使用轮盘赌的方法。解决路径规划的优化问题必须要先解决问题模型中的约束条件问题,包括一些等式和不等式的约束条件,在遗传算法中对约束条件的处理会带来一些额外的参数。首先要将所有的等式约束条件转化成不等式约束条件,这样就只处理不等式约束条件即可。文中采用静态惩罚函数法来处理不等式约束条件,适应度函数定义为:
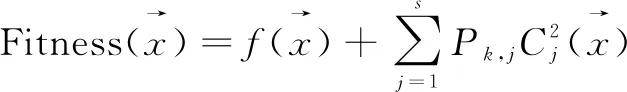
(7)
3.4 交叉运算
交叉运算产生子代,子代继承父代的基本特征,主要包括两个内容:第一是对种群中的个体进行随机配对并按照设定的交叉概率Pm来确定需要交叉的个体对;第二是设定个体的交叉点,然后对个体的部分片段相互交换。交叉算子的设计与编码方式有关,在最优路径规划问题中有几种代表性的交叉算子,如:顺序交叉、类OX交叉等。这些交叉算子在产生新个体的过程中没有目的性,对于实数编码的最优规划问题,这些交叉可能破坏亲代的较优基因,从而使交叉算子的搜索能力大大降低。基于此,文中拟用在重复节点位置交叉且只进行一点交叉的操作方式,具体实现步骤如下:
·随机选取两个个体作为带交叉个体;
·找到两个带交叉个体的共同点(源节点和目的节点除外)的集合;
·从共同节点的集合中随机选择一个节点作为交叉节点;
·检查两个带交叉个体在交叉节点之前和之后的内容是否相同。如果相同,则取消此次的交叉操作。
具体的操作过程如下:
(1)设选取的两个待交叉样本为0.0,3.5,50.9,70.3,62.8,109.5,120.4和0.0,23.1,50.9,25.6,62.8,98.5,120.4,如图2所示;
(2)两者重复节点为{50.9,62.8};
(3)随机选择节点50.9作为交叉节点;
(4)检查发现两者带交叉样本在节点50.9之前和之后的内容均不相同,因此可以进行此次操作,交叉之后会产生新的个体:
0.0,3.5,50.9,25.6,62.8,98.5,120.4
0.0,23.1,50.9,70.3,62.8,109.5,120.4
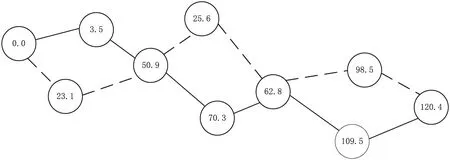
图2 交叉操作
3.5 变异操作
变异操作是对个体的某些基因值做变动。目的有两个,第一使遗传算法具有局部的随机搜索能力,当经过交叉操作群体已接近最优解时,利用变异算子可以加速向最优解收敛;第二是使遗传算法可维持群体的多样性,以防止早熟现象。变异算子的设计也与编码方法有关,对于实数编码的TSP问题,可采用逆转变异、对换变异和插入变异等。逆转变异,也称倒位变异,是指在个体编码中随机选择两点,再将这两点内的字串按反序插入到原位置中。倒位变异考虑了与原边的邻接关系,能将巡回路线上的优良基因性能较好地遗传到下一代,提高寻优速度。基于此,该项目具体实现步骤如下:
(1)随机选取一个个体作为待变异个体;
(2)在待变异个体中随机选择一个节点(起点和终点除外)作为待变异节点;
(3)找到与当前待变异节点直接相连的节点集合(该集合中不包括起点、终点以及待变异个体中的节点);
(4)从节点集合中随机选取一个节点作为变异后节点;
(5)检查待变异节点之前和之后的节点是否与变异后节点直接相连。若直接相连,则用变异后节点替代待变异节点完成变异过程;否则,放弃此次操作,回到第4步,直至将节点集合中的所有节点全部选遍。
操作的实现过程如下:
(1)选择待变异的个体为0.0,23.1,50.9,70.3,62.8,109.5,120.4,如图3所示;
(2)随机选择节点50.9为变异节点;
(3)与节点50.9直接相连的节点集合为{3.5,31.9,25.6};
(4)随机选择节点3.5作为变异后节点;
(5)经过检查发现节点23.1与节点3.5并不直接相连,所以取消此次变异操作,接着选取节点31.9作为变异后的节点,检查后发现节点23.1和节点31.9、节点31.9和节点70.3直接相连,所以此次变异操作是可以的,变异后的新个体为:0.0,23.1,31.9,70.3,62.8,109.5,120.4。
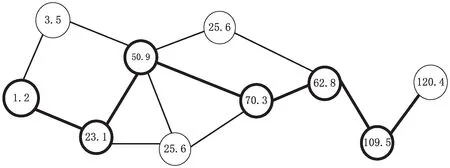
图3 变异操作
3.6 终止条件
初始种群规模相对较大或者网络拓扑规模相对较小时,算法收敛速度则相对较快。基于这一原因,算法终止条件选定为“迭代达到最大世代数”或者“种群中半数以上位置被生成的最优个体占据”。
3.7 算法完整流程
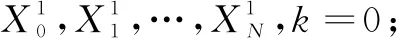
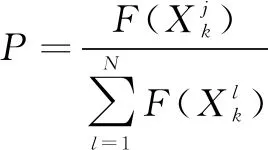
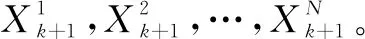
第六步:检查代数是否已经达到设定的值,如果满足则停止遗传算法,否则重复第二步。
4 实验仿真与分析
实验的网络路由模型采用满足多约束的最小费用模型,网络规模为500节点24 k链路,费用和时延皆在[1,10]中随机选取。带宽以1 M为单位,链路的带宽分别在10 G、20 G、30 G、40 G中随机选取,随机网络生成后,随机选取源点和宿点并用最短路算法求解最小时延路的时延D1和最小费用路的时延D2,取d=(D2-D1)/4。时延约束取不大于D2+d;请求的业务的带宽要求在1 G、800 M、500 M、50 M中随机选取,跳数约束为不大于80跳。
图4的实验结果是在初始种群规模为50,交叉变异概率分别为0.5,0.3的情况下生成的,由此说明文中算法对这种大规模的约束网络模型具有比较快的收敛速度。
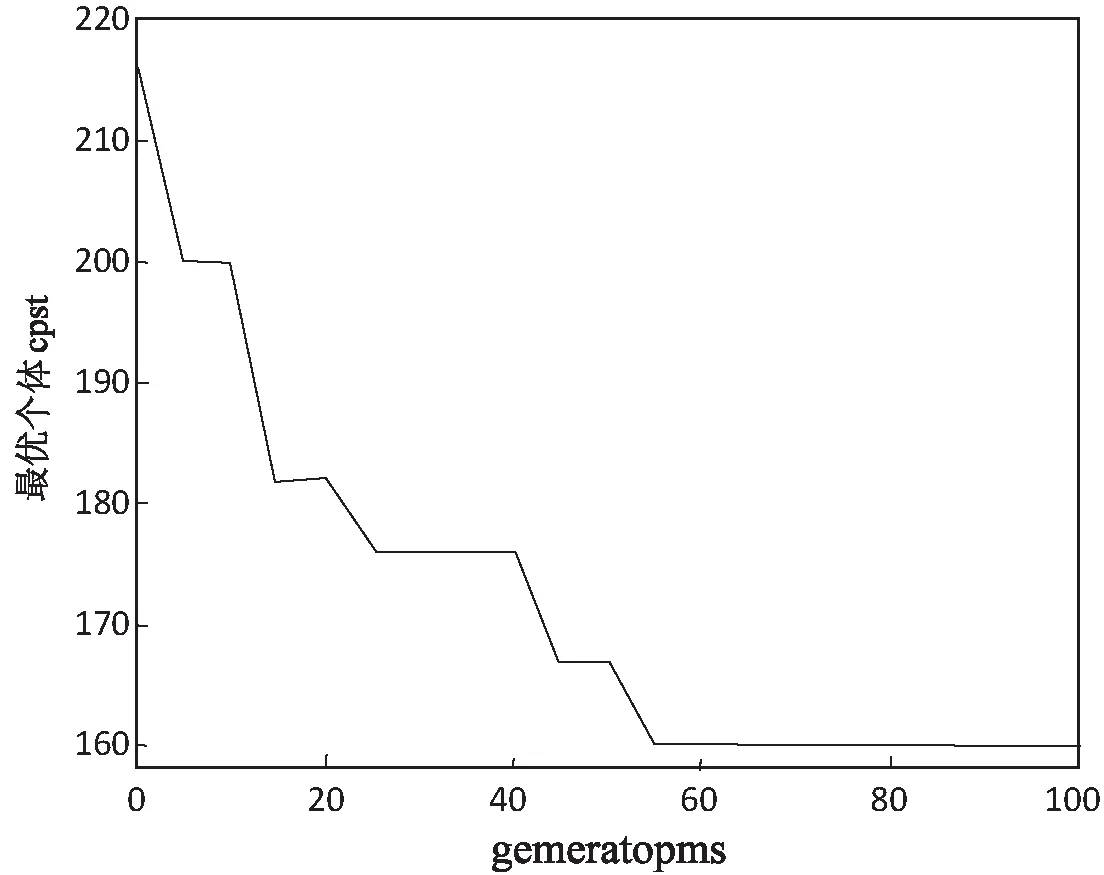
图4 遗传代数与最优个体适应度值的变化
Dijkstra算法在求解最短路径的过程中,无论起始节点距离终点多远都需要遍历整网的拓扑,在节点数为n的网络中,Dijkstra算法的复杂度为O(n)。对于节点数和边数比较大的大规模图,当n比较大时,该算法所需计算机的时间资源与空间资源将急剧增加;对GA算法,路径长度主要影响算法的收敛时间,GA算法的搜索空间大小为路径的长度,所以根据算法的特点决定文中的遗传算法更适合大规模网络路径的计算。图5是KSP算法和改进遗传算法同时计算10条无约束路径的耗时,实验结果也验证了这个结论。
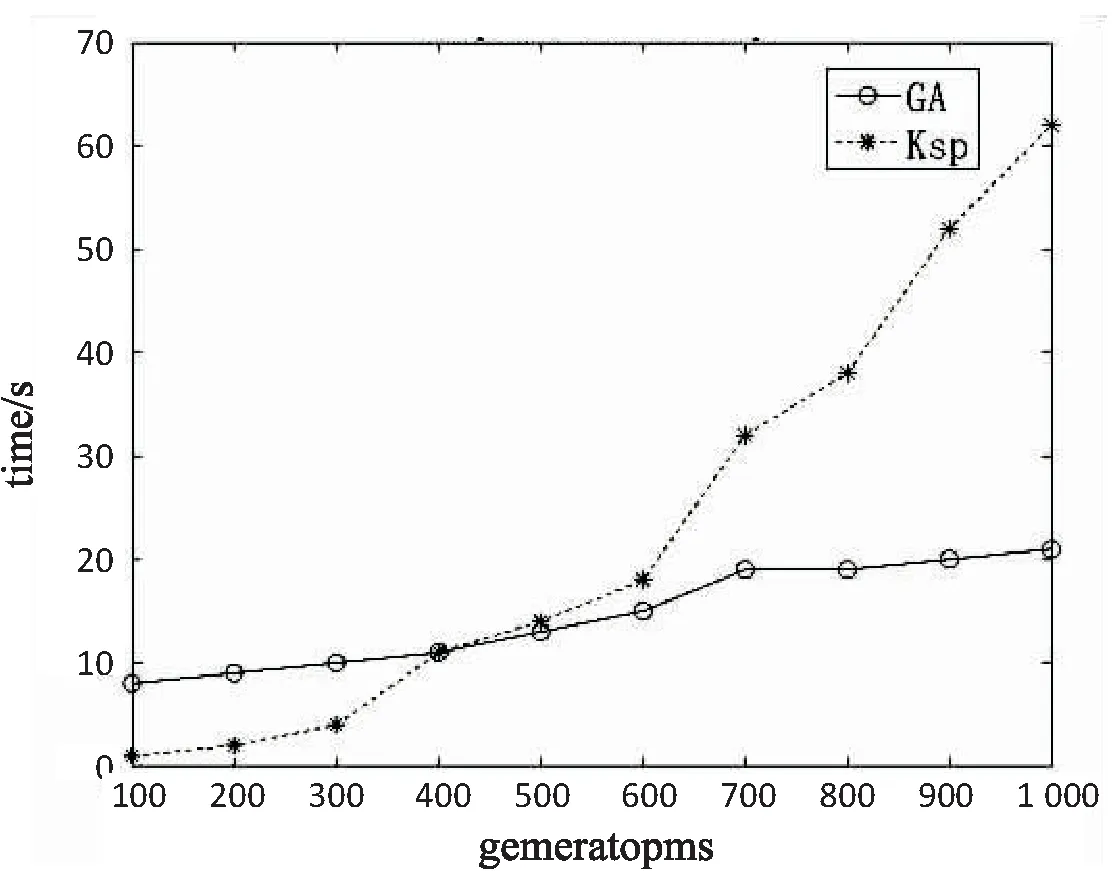
图5 KSP算法与文中算法的耗时比较
5 结束语
文中提出的基于多目标多约束的改进遗传算法可以在保证一定性能的前提下,在大规模网络中计算出符合所有约束的最优路径。并且,该算法主要具有以下特点:改进了初始路径的生成方式,显著提高了算法的搜索效率,可以解决严格下一跳和松散下一跳的约束;实数编码,简化了编码和解码的操作,省略了复杂的解码过程;启发式交叉策略,加快了算法收敛的速度;该算法较传统的K最短路径算法更适合大规模网络路径的计算。
