应用单层超表面实现声波宽角度非对称传输

李冰，徐辉宇，何灵娟，于天宝，刘文兴，王同标，刘念华，廖清华

应用单层超表面实现声波宽角度非对称传输

李冰1，徐辉宇1，何灵娟1，于天宝1，刘文兴1，王同标1，刘念华2，廖清华1

(1. 南昌大学物理系，江西南昌 330031；2. 南昌大学高等研究院，江西南昌 330031)

利用单层梯度超表面结构，设计并模拟验证了一种实现声波非对称传输的方法，在较宽的角度范围内实现了高对比度的声波非对称传输。经过恰当的超表面结构设计后，负折射现象实现了声波的正向导通；高阶衍射的抑制导致了反向入射的声波传输被禁止。基于广义斯涅耳定律分析了非对称传输的原理，采用有限元法的数值模拟结果很好地验证了理论分析。研究结果在噪声控制、超声整流或治疗等方面具有潜在的应用价值。

声学超表面；梯度超表面；非对称传输；有限元法

0 引言

声学超表面是由亚波长尺寸的结构单元在一个平面上排列而成的准二维结构[1-2]。超表面中每个单元对入射波的声学响应(包括幅值、相位)可以独立控制，通过调节超表面单元的声学响应，可形成幅值、相位的重新分布，进而实现对入射波的几乎任意的操控。利用超表面可以实现声波的许多功能，如波束偏转[3-5]，声波的聚焦[6-7]和完美吸收[8]等。

作为一类十分重要的声学现象，非对称或单向传输已经得到了大量的研究。在实现声学非对称传输的传统方法中，一方面，可利用非线性机制，打破时间反演对称[9-10]，但这种方法存在非线性转化效率低、实验实现复杂等缺点；另一方面，也可采用非对称几何结构，破坏空间反演对称[11-12]，但该方法存在着器件制作复杂、体积较大等问题，这都妨碍了声学非对称性传输的进一步的实际应用。近些年来，声学超表面的出现为实现声学非对称传输提供了一条有效的新途径。常见的报道是采用混合超表面结构实现声波的非对称传输[13-15]。混合超表面结构可由声学超表面和声子晶体组合构成[13]，也可由两个或两个以上的声学超表面构成[14-15]。混合超表面结构的子单元通常采用了不同的设计方法。如梯度超表面和声子晶体的组合[13]，在同一频率下，利用超表面能够改变声波传播方向和声子晶体特定方向存在通带或禁带的特点，从而实现声波的非对称传输。对于多个超表面结构的组合[14-15]，通过设计不同的超表面几何结构，造成不同超表面的有效折射率不同，当声波从有效折射率较大的超表面一端入射时，在两个超表面的界面出现全反射的现象，进而实现了声波的非对称传输。显然，这类混合超表面的组合单元有着两层或两层以上的不同结构，因此仍然存在着设计和制备复杂、器件难以实现集成等问题。

最近，LI等[16]仅仅采用单层梯度超表面就实现了声波的非对称传输，其物理机制是通过引入固定损耗抑制了反向传输时的高阶衍射，导致了声波的反向传输消失。在没有引入损耗的情况下，LIU等[17]把单层超表面平均分割成两个超表面，通过超表面之间声波的相干效应实现了声波的非对称传输。本文采用类似的单层梯度超表面，既无需引入损耗，亦无需分割超表面，通过合理的设计，在声波反向传输时，高阶衍射被抑制，实现了声波宽角度、高对比度的非对称传输。

1 理想模型和原理

首先，我们采用一个理想超表面模型说明声波的非对称传输机制。声学超表面结构为单层，由周期性的超胞构建而成。图1(a)分别给出了声波沿正方向(Positive Direction, PD)、反方向(Negative Direction, ND)入射到声超表面时声波的传输途径。入射角为，当声波沿正方向斜入射时，声波实现了负折射，从而实现了正向导通；当声波沿负方向斜入射时，传输声波转换成了表面波，负方向无法导通，因此形成了典型的声学非对称传输现象。

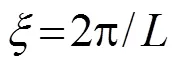
图1 基于单层声学超表面的非对称性传输示意图和超胞结构示意图

图2 理想超表面结构中声波实现单向传输的声压分布图

下面分析这种非对称传输的现象，入射声波满足广义斯涅尔折射定律[21]：

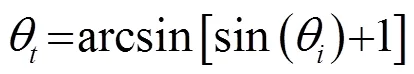
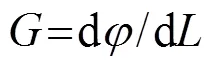
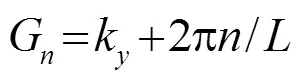
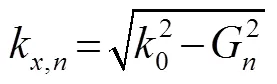
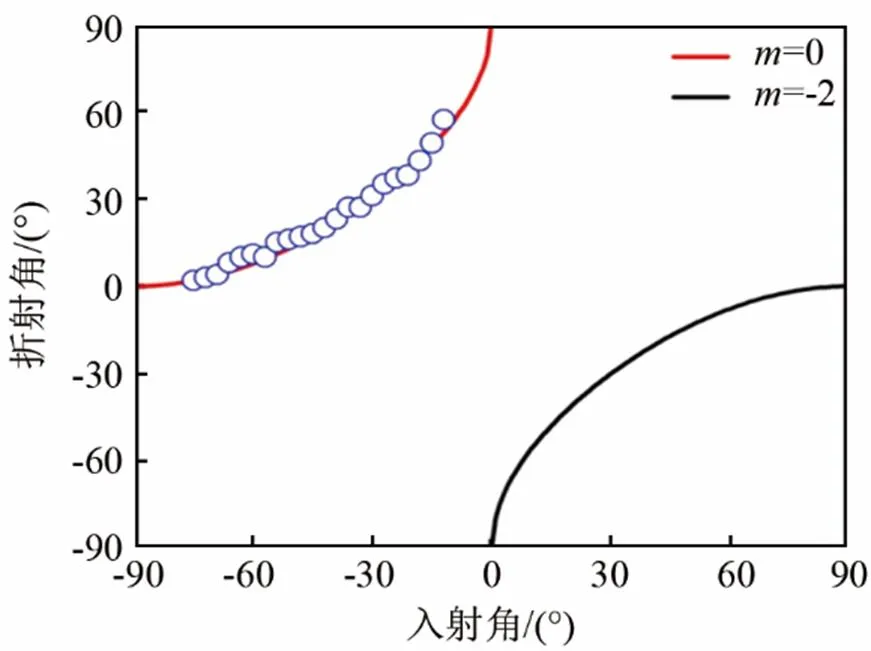
图3 M=17时，折射角与入射角之间的关系

2 实际超表面的设计及模拟分析

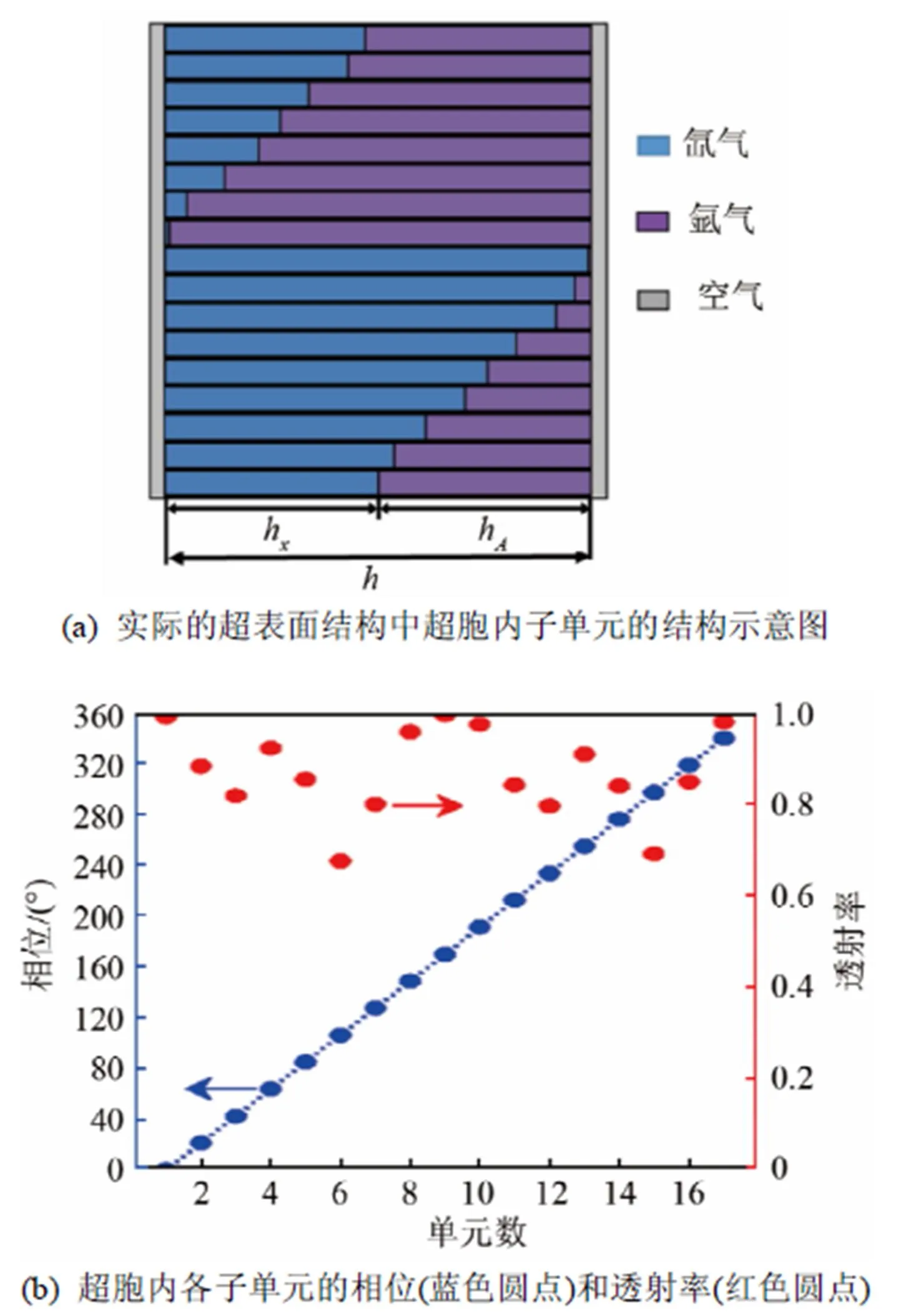
图4 实际超表面的结构示意图以及各子单元的相位和透射率

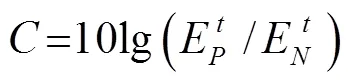
上述的模拟结果仅考虑了单个入射角，为了讨论该非对称传输器件的入射角容差，图6(a)给出了在同一频率3 430 Hz时，该超表面结构中透射声能量对比度与入射角的对应关系。很明显地可以看出，入射角从20º～65º的宽角度变化时，正反方向入射的对比度>15 dB，且在入射角为24º时达到了峰值17.41 dB，因此本文设计的非对称传输对入射角度非常不敏感，实现了很大的入射角度容差。在损耗型单层超表面实现的非对称传输中[16]，对比度的峰值仅约为10 dB，实现了15º～45º之间的>6 dB的能量对比度；与双层耦合型超表面形成的非对称传输性能相比[17]，本文的对比度的峰值提高了约3.81 dB，在20º～65º之间对比度普遍提升了近3 dB。因此，本文设计的非对称传输器件与之前报道的结果相比，虽然结构相似，但非对称传输的性能得到了显著的提升。随后，固定入射角为24º，计算得到了工作频率从3 300～3 500 Hz的非对称传输性能，透射能量对比度与频率之间的变化关系如图6(b)所示。在中心工作频率(3 430 Hz)处达到最大值17.41 dB。一般对比度>6 dB时可以认为该结构具有了较好的非对称传输性能[16]，从图中可以看出，对比度>6 dB的频率范围分布于3 360～3 450 Hz之间，结果表明，在中心工作频率附近较宽的频率区间具有很好的非对称传输性能。

图5 实际设计的超表面结构中声波实现单向传输的声压分布图

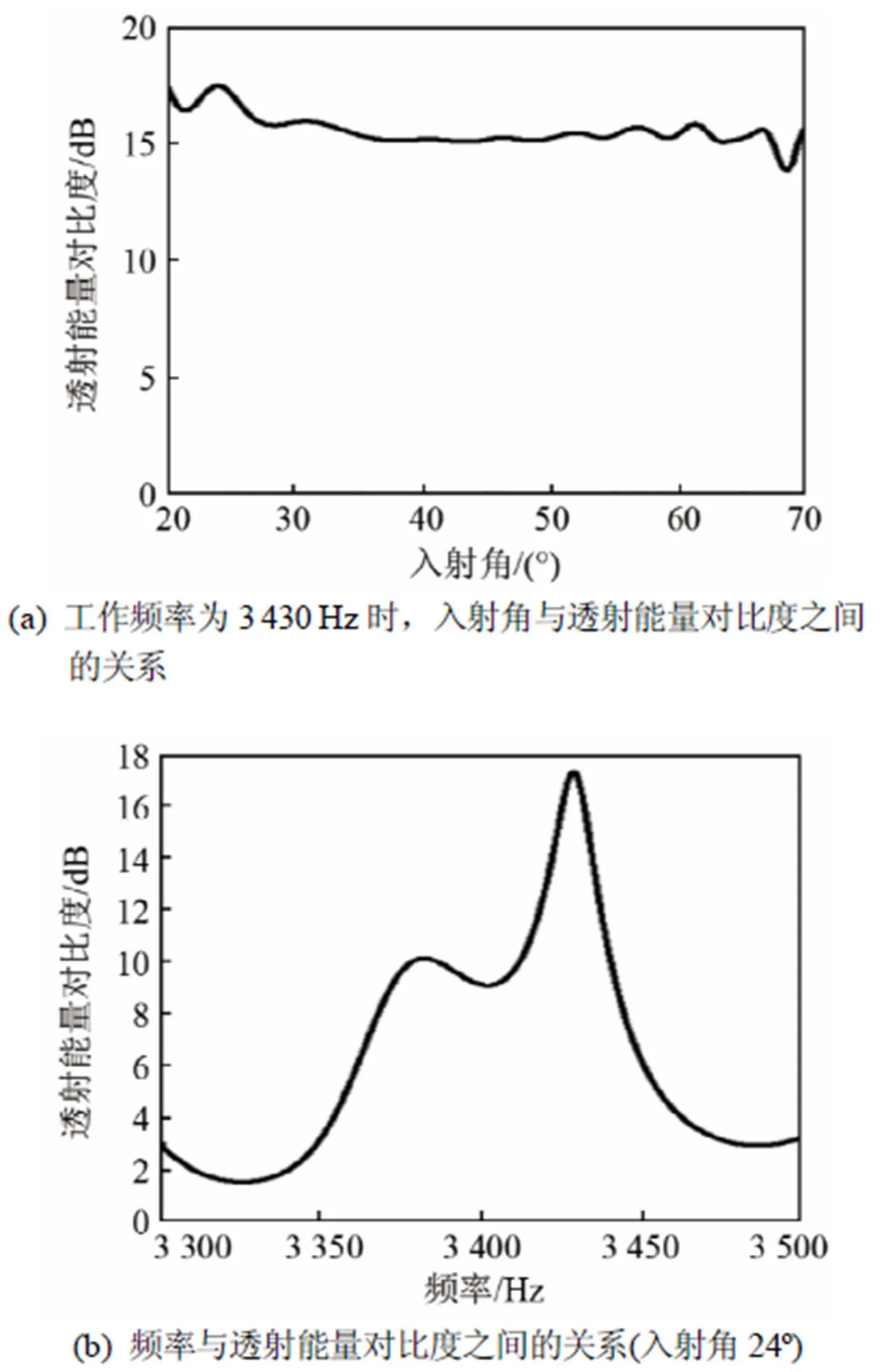
图6 透射能量对比度与入射角、频率之间的关系

3 结论

本文设计、分析及模拟了一种基于单层声学梯度超表面的宽角度、高能量对比度的非对称传输结构。正向斜入射时，负折射实现了声波的正向导通；反向斜入射时，使超胞相位梯度和自由波矢相等，实现了高阶衍射的抑制，从而禁止了声波的反向传输。理论分析和数值模拟结果表明，透射能量对比度的峰值可达17.41 dB，在20º～65º的宽角度范围内，对比度>15 dB。与之前报道的结果相比，本文的研究结果展现了更优的非对称传输性能。

[1] 丁昌林, 董仪宝, 赵晓鹏. 声学超材料与超表面研究进展[J]. 物理学报, 2018, 67(19): 10-23.

DING Changlin, DONG Yibao, ZHAO Xiaopeng. Research advances in acoustic metamaterials and metasurface[J]. Acta Phys. Sin., 2018, 67(19): 10-23.

[2] ASSOUAR B, LIANG B, WU Y, et al. Acoustic metasurfaces[J]. Nat. Rev. Mat., 2018, 3(12): 460-472.

[3] LI Y, QI S B, ASSOUAR B M. Theory of metascreen-based acoustic passive phased array[J]. New J. Phys., 2016, 18: 043024-1-19.

[4] HAN L X, YAO Y W, ZHANG X, et al. Acoustic metasurface for refracted wave manipulation[J]. Phys. Lett. A, 2018, 382(5): 357-361.

[5] LI Y, LIANG B, GU Z M, et al. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces[J]. Sci. Rep., 2013, 3:2546-1-6.

[6] QI S B, ASSOUAR B M. Ultrathin acoustic metasurfaces for reflective wave focusing[J]. J. Appl. Phys., 2018, 123(23): 234501-1-8.

[7] QI S B, LI Y, ASSOUAR B M. Acoustic focusing and energy confinement based on multilateral metasurfaces[J]. Phys. Rev. Applied, 2017, 7(5): 054006-1-16.

[8] LI Y, ASSOUAR B M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness[J]. Appl. Phys. Lett., 2016, 108(6): 063502-1-4.

[9] 林洲, 郭霞生, 程建春, 等. 声二极管中声传播模型研究[J]. 声学技术, 2013, 32(5): 353-356.

LIN Zhou, GUO Xiasheng, CHENG Jianchun, et al. Research on sound propagation model in acoustic diode[J]. Technical Acoustics, 2013, 32(5): 353-356.

[10] KAN W W, LIANG B, ZHU X F, et al. Acoustic one-way frequency up-converter with high transmission efficiency[J]. J. Appl. Phys., 2013, 114(13): 134508-1-6.

[11] 程营, 吴大建, 刘晓峻. 表面声学超构材料中的非对称声传输研究[J]. 声学技术, 2013, 32(5): 33-34.

CHENG Ying, WU Dajian, LIU Xiaojun. Asymmetrical transmission of sound wave in acoustic surface metamaterials[J]. Technical Acoustics, 2013, 32(6): 33-34.

[12] HE Z J, PENG S S, YE Y T, et al. Asymmetric acoustic gratings[J]. Appl. Phys. Lett., 2011, 98(8): 083505-1-3.

[13] SONG A L, CHEN T N, WANG X P, et al. Waveform-preserved unidirectional acoustic transmission based on impedancematched acoustic metasurface and phononic crystal[J]. J. Appl. Phys., 2016, 120(8): 085106-1-7.

[14] CHEN D C, ZHU X F, WEI Q, et al. Asymmetric phase modulation of acoustic waves through unidirectional metasurfaces[J]. Appl. Phys. A, 2018, 124(1): 1-6.

[15] SHEN C, XIE Y B, LI J F, et al. Asymmetric acoustic transmission through near-zero-index and gradient-index metasurfaces[J]. Appl. Phys. Lett., 2016, 108(22): 223502-1-4.

[16] LI Y, SHEN C, XIE Y B, et al. Tunable asymmetric transmission via lossy acoustic metasurfaces[J]. Phys. Rev. Lett., 2017, 119(3): 035501-1-5.

[17] LIU B Y, JIANG Y Y. Controllable asymmetric transmission via gap-tunable acoustic metasurface[J]. Appl. Phys. Lett., 2018, 112(17): 173503-1-5.

[18] 周光平, 杨奇, 李自光, 等. 超声换能器激励的板声源振动特性的有限元分析[J]. 声学技术, 2007, 26(2): 326-329.

ZHOU Guangping, YANG Qi, LI Ziguang, et al. Finite element analysis of transducer-driven vibration of plate[J]. Technical Acoustics, 2007, 26(2): 326-329.

[19] WANG Z, YU T B, WANG T B, et al. Acousto-optic interactions for terahertz wave using phoxonic quasicrystals[J]. J. Phys. D: Appl. Phys., 2018, 51(10): 1-10.

[20] YU T B, WANG Z, LIU W X, et al. Simultaneous large band gaps and localization of electromagnetic and elastic waves in defect-free[J]. Opt. Express, 2016, 24(8): 7951-7959.

[21] YU N F, GENEVET P, KATS M, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction[J]. Science, 2011, 334(6045): 333-337.

[22] QIAN E T, FU Y Y, XU Y D, et al. Total omnidirectional reflection by sub-wavelength gradient metallic gratings[J]. Europhys. Lett., 2016, 114(3): 34003-1-5.

[23] MEI J, WU Y. Controllable transmission and total reflection through an impedance-matched acoustic metasurface[J]. New J. Phys., 2014, 16: 123007-1-11.

Wide-angle asymmetric sound wavetransmission in the single-layer metasurface

LI Bing1,XU Hui-yu1,HE Ling-juan1,YU Tian-bao1,LIU Wen-xing1,WANG Tong-biao1,LIU Nian-hua2,LIAO Qing-hua1

(1. Department of physics, Nanchang University, Nanchang 330031, Jiangxi, China; 2.Institute for Advanced Study, Nanchang University, Nanchang 330031, Jiangxi, China)

Based on the single-layer acoustic gradient-index metasurface, a method of realizing acoustic asymmetric transmission is designed and simulated. The asymmetric transmission exhibits the characteristics of wide-angle and high energy contrast. Via proper design of metasurface structure, positive propagation is permitted by negative refraction and negative propagation is prohibited by suppressing high order diffraction. The results of theoretical analysis using the generalized Snell’s law agree well with those of simulation based on finite element method. The design has potential application values in noise control, ultrasonic rectification and treatment.

acoustic metasurface; gradient metasurface; asymmetric transmission; finite element method

O424

A

1000-3630(2019)-03-0253-05

10.16300/j.cnki.1000-3630.2019.03.003

2018-12-26;

2019-03-14

国家自然科学基金(11664024、11704175)、江西省杰出青年基金(20171BCB23009)和江西省自然科学基金重点项目(20171ACB21020)资助。

李冰(1990－), 男, 河北邢台人, 硕士, 研究方向为声学超表面。

何灵娟,E-mail: helingjuan_123@163.com