服务半径约束下城市快递双层配送网络节点选址优化

杜刚诚 冉林娜

摘要：为提高快递配送效率，基于城市快递双层配送网络的构成和优势，建立该网络二级节点选址模型，包括末端配送站点和便民寄存点选址，其中便民寄存点选址需考虑服务半径约束和容量限制。提出分解算法进行模型求解，其中针对便民寄存点选址采用改进的最少点覆盖启发式算法，针对末端配送站点选址采用k-均值聚类算法。利用算例进行模型和算法验证，结果表明，该模型和算法能有效解决城市快递双层配送网络的节点选址优化问题。

关键词：物流规划;城市快递;双层配送网络;节点选址

中图分类号：U294.1

文献标志码：A

Abstract：In order to improve the efficiency of express delivery， based on the structure and advantages of the double-layer distribution network of urban express delivery， a two-level node location model of the network is established， where the nodes include the terminal distribution stations and temporary storage stations， and the service radius constraint and capacity constraint are considered in the location of temporary storage stations. A decomposition algorithm is used to solve the model， where an improved least point coverage heuristic algorithm is applied to the node location of temporary storage stations， and the k-means clustering algorithm is applied to the node location of terminal distribution stations. An example is used to verify the model and the algorithm. The result shows that the model and the algorithm can effectively solve the node location optimization problem of the urban express double-layer distribution network.

Key words：logistics planning; urban express delivery; double-layer distribution network; node location

收稿日期：2018-05-14

修回日期：2018-08-30

作者简介：

杜刚诚（1977—），男，湖北秭归人，高级工程师，硕士，研究方向为城市规划、交通规划，（E-mail）dgch2002@163.com

*通信联系人。 （E-mail）ranlinna@126.com

0 引 言

近年来我国电子商务发展迅速，快递业务量不断增长，快递作为物流产业的一个重要组成部分，逐渐渗透到社会经济的各个领域。合理的配送网点布局可以提高配送资源的利用率，降低企业运营成本。以往快递配送企业多采用单层配送模式。快递单层配送网络通常由两级节点构成：一级节点即快递分拨中心，一般设立在机场、铁路货站、公路货站等大型交通枢纽，负责对快递进行城市间的集散和转运;二级节点即快递末端配送站点，一般会设在各个城市分区，负责对快递进行配送并兼顾快递揽收业务。在这种单层配送模式下，快递末端配送站点配送人员工作量过大，快递配送效率低，因此，很多快递配送企业已经开始采用双层配送模式。快递双层配送网络通常由三级节点构成：一级节点即快递分拨中心;二级节点即快递末端配送站点;三級节点即快递便民寄存点。一般一个便民寄存点负责对一个或多个居民小区快递的寄存和配送。为更好地服务客户、扩大市场份额，研究快递企业的网点布局及其优化具有现实意义。

近年来，针对快递配送网络的研究主要有：张哲辉[1]提出了快递网络的构成，即“取送—集散—网路”，并运用数学和管理学方法，详细分析了快递市场的发展因素;张兰[2]建立了快递网络覆盖模型和中转场选址模型，并给出拆分和合并两种模式下网点布局优化的策略;焦艳[3]将网络成本最小作为最终目标，建立了基于城市电子商务的物流网络选址多目标模型，采用遗传算法和禁忌搜索算法分别对配送区域、选址分配、路径优化问题进行了求解;丛迪悦[4]建立了快递企业服务网点布局优化策略模型，建立了基于层次分析法和成本约束条件的目标规划模型，最终完成了快递网点整体布局优化;杨从平等[5]以配送时间和节点流量作为约束条件进行快递网络优化，将网络配送总成本最小化作为优化目标，运用Floyd算法和Dijkstra算法进行了求解;卢文涛[6]在考虑时间阈值的基础上构建了快递网络优化模型，基于成本惩罚和严格时间阈值构建了数学模型，同时用摩西网络进行了演算;程赐胜等[7]在假定城市物流系统运行费用最低的条件下构建了城市物流节点选址模型，并用离散粒子群优化算法对该模型进行了求解。

上述研究主要针对快递配送节点选址的模型和算法设计，较少涉及对快递企业双层配送网络及其节点选址的研究。本文在分析城市快递双层配送网络构成的基础上，建立考虑便民寄存点服务半径约束的快递双层配送网络模型，并提出分解算法求解模型，分别就便民寄存点选址和末端配送站点选址提出改进的最少点覆盖启发式算法和k-均值聚类算法，借助算例进行了模型和算法的验证。

1 考虑服务半径约束的快递配送网络模型建立为提高快递配送效率，便民寄存点选址需要考虑合适的服务范围。从城市物流网络规划的角度出发，快递末端配送站点与便民寄存点联动配合形成网络。城市快递双层配送网络示意图见图1。

快递双层配送模式一方面能够分割城市配送区域，便于快递配送人员熟悉掌握地理位置，另一方面可有效减少单个配送点负责的客户数量，提高快递配送效率。在建立城市或区域的快递配送网络时，往往已知各快递分拨中心的数量、位置和快递业务量，只需进行末端配送站点和便民寄存点的选址。本文以居民小区中心点代表客户点。

1.1 问题描述

某地区有若干居民小区，已知该地区快递分拨中心数量、位置和各小区快递业务量，现欲在各居民小区周边建立便民寄存点，为各居民小区客户提供上门配送快递服务。若便民寄存点与居民小区中心点之间的距离超过限值则不予配送;选择合适的位置建立末端配送站点。本文只考虑前期建设成本，不考虑后期运营成本，选择改进的最少点覆盖模型进行求解，建立模型的目标为用最少的末端配送站点和便民寄存点服务所有的客户。

1.2 假设条件

为简化配送节点选址问题，假设：（1）已知快递分拨中心数量、位置;（2）各居民小区需求必须得到满足，一个居民小区由一个便民寄存点服务;（3）便民寄存点多建在小区周边，不宜过大，因此有容量限制;（4）末端配送站点没有容量限制;（5）从各快递分拨中心到各小区的快递业务量已知;（6）便民寄存点有服务半径约束，与小区中心点之间的距离超过限值即不予服务;（7）快递以件计。

1.3 模型参数设定

N为居民小区（客户）集合，i∈N;S为便民寄存点集合，j∈S;R为末端配送站点集合，k∈R;M为分拨中心集合，m∈M;l为便民寄存点服务半径约束;qim为从分拨中心m配送到居民小区i的快递量;qij为从便民寄存点j配送到居民小区i的快递量;qjk为从末端配送站点k到便民寄存点j的快递量;qkm为从分拨中心m到末端配送站点k的快递量;qkk′为从末端配送站点k到末端配送站点k′的路径上分配的快递量;Qj为便民寄存点j的容量限制;A（j）为便民寄存点j所服务的居民小区的集合;B（i）为服务居民小区i的便民寄存点j的集合;C（k）为末端配送站点k所服务的便民寄存点j的集合;xj为0-1变量，xj=1表示备选点j被选中作为便民寄存点，否则xj=0;yk为0-1变量，yk=1表示备选点k被选中作为末端配送站点，否则yk=0;zmk为0-1变量，zmk=1表示分拨中心m与末端配送站点k之间有路径连接，否则zmk=0;Qkk′为0-1变量，Qkk′=1表示末端配送站点k与k′之间有路径连接，否则Qkk′=0。

1.4 模型建立

式（1）和（2）为模型建立的目标，式（1）表示用最少的便民寄存点服务所有的居民小区，式（2）表示用最少的末端配送站点覆盖所有的便民寄存点。式（3）～（6）为模型的约束条件，式（3）表示居民小区的所有快递量都被处理，式（4）表示一个居民小区只能由一个便民寄存点服务，式（5）为便民寄存点容量限制，式（6）为便民寄存点服务半径约束。

2 求解算法设计

本文建立的模型需要求解以下问题：确定末端配送站点和便民寄存点的位置及其服务范围。本文采用分解法进行求解，将该问题分解为两个相互衔接的子问题，即先确定便民寄存点的位置及其服务范围，然后求解末端配送站点的位置及其服务范围，第二个子问题的解建立在第一个子问题解的基础上。

2.1 便民寄存点选址求解算法

采用改进的最少点覆盖启发式算法求解，主要步骤如下：

步骤1 初始化。令所有qij=0，xj=0，并确定集合A（j），同时保证备选点i与j之间的距离小于服务半径l。

步骤2 选择下一个便民寄存点。在S中选择xj=0且A（j）的模为最大的点j′为便民寄存点，即A（j′）=maxj∈M{A（j）}，xj′=1，并在S中剔除节点j′，即S=S{j′}。

步骤3 确定便民寄存点j′的覆盖范围。令zi=1， 居民小区i已被便民寄存点覆盖0， 其他

令qi=m∈Mqim，将A（j′）中的元素按qi从大到小的顺序分配給j′，直至j′的容量达到最大且不超过容量限制或A（j′）为空。为保证每个便民寄存点的最大利用率，若加入新元素后累计容量超过限制，则跳过该项尝试下一元素，直到容量已满或A（j′）为空。其中，对于i∈A（j′）且zi=0，将i指派给j′的方法为：令qij=qi，若qij（1-zi）≤Qj′，则Qj′=Qj′-qij（1-zi），zi=1，并在A（j′）和N中剔除居民小区i;若qij（1-zi）>Qj′，qij=0，则跳过该项尝试下一居民小区。

步骤4 若N和S为空，则停止，否则更新集合A（j），转步骤2。

2.2 末端配送站点选址求解算法

2.2.1 数量确定

假设：（1）所规划区域的总面积为A′，快递总需求量为G;（2）区域内的快递需求量平均分布，各末端配送站点的规模相同，且位于其服务区域的中心;（3）相同规模的末端配送站点在区域内各处的建设费用相等，即末端配送站点的建设费用与位置无关。

设当区域的末端配送站点数为n时，区域内快递配送总成本为Cz（n），Cz（n）又由快递配送成本Cd和快递配送站建设成本Cs两项组成。由假设（1）和（2）有：每个末端配送站点服务范围的面积a相同，a=A′/n;每个末端配送站点的快递处理量g相同，g=A′/n。

末端配送站点配送的平均距离d与服务范围面积a的平方根成正比，即d=θfa，式中：θ为平均配送距离参数，与配送区域的形状有关，如当配送区域为圆形时θ可取0.376，当配送区域为正方形时θ可取0.383，当配送区域为长宽比为2∶1的长方形时θ可取0.42;f为非直线系数，一般可取1.2。

快递配送的主要内容包括配货、装载、运输、卸载、车辆返回等几项工作，其中：配货、装载、卸载这3项工作的费用与运输距离无关，只与快递量成正比（设比例系数为b）;运输、车辆返回这2项工作则与运输距离成正比。因此，快递的配送成本可表示为

式中：k′为快递配送单位成本。末端配送站点的建设费用包括两部分：一部分是征地、仓库堆场建设、设备购买的费用，这部分费用与末端配送站點的规模成正比，亦即与快递处理量成正比（设比例系数为r）;另一部分是固定费用C0，如附属设施建设费用等。因此，末端配送站点的建设费用可表示为

总成本为

区域内快递配送总成本Cz（n）与末端配送站点数量n之间的关系为

确定区域最佳末端配送站点数量问题就是要求整数n，使上式中Cz（n）取值最小。先设n为实数变量，Cz（n）为n的连续函数，令

比较在n分别为

分别表示不大于X的最大整数和不小于X的最小整数。当n=Gk′θfA′2C02/5时总成本最小。

2.2.2 选址算法

得到需建设的末端配送站点数量后，就可以开始进行选址。本文采用k-均值聚类算法进行求解。k-均值聚类算法基于各个类内的数据点与所在类质心的误差平方和最小原则，将数据点分为具有相似特征的k个簇。也就是说，将含有n个样本数据的集合X=

{s1，s2，…，sn}划分为k类（C1，C2，…，Ck），其中每个数据点只能归属为一类。

k-均值聚类算法最小化目标函数为

式中：sj为第i类Sj中的样本;mi为第i类的聚类中心，即第i类样本数据的均值;sj-mi2为第i类内各样本与聚类中心的欧氏距离。

3 算例分析

为分析模型算法有效性，选取某快递配送企业在M市的业务情况作为算例进行验证。某快递企业将该市划分为105个居民小区，在该市设有A、B、C、D等4个快递分拨中心。为满足客户需求，该企业计划在该市建立一个完善的配送网络：首先，在居民小区周边建立服务半径为3 km的便民寄存点，客户以居民小区中心点代替，本市所有居民小区周边都可以建立便民寄存点，因此其备选位置集合即所有居民小区集合;其次，在合适位置建立合适数量的末端配送站点，并确定相应的配送方案。

图2为该企业业务情况分布图;表1列出了4个分拨中心和居民小区的编号和坐标，各节点之间距离用欧氏距离表示;表2列出了M市的4个分拨中心某天需要配送到各居民小区的快递量。

3.1 便民寄存点选址

用MATLAB对模型算法进行编程求解，最终得到42个便民寄存点。表3为便民寄存点选址及分配方案，图3为便民寄存点选址结果。

3.2 末端配送站点选址

末端配送站点数量计算。取G=26 142件，A′=294 km2，θ=0.42，f=1.2，C0=2亿元，k′=0.02元/（件·km）（为市场调研均价），n=Gk′θfA′2C02/5，计算可得7个末端配送站点。

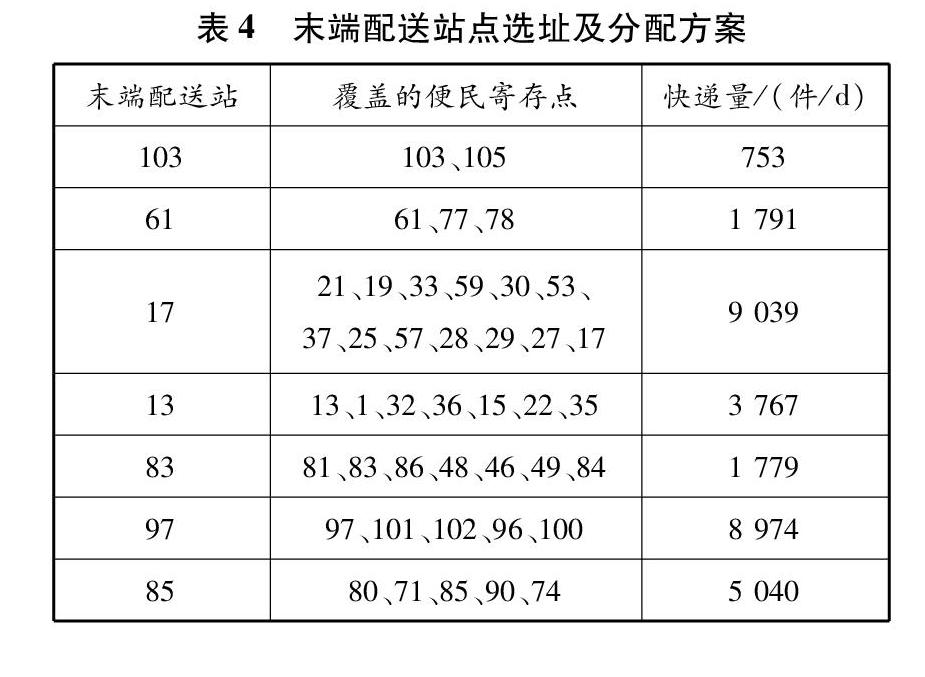
末端配送站点选址。在已选好的便民寄存点中选择末端配送站点。假设可同时建设末端配送站点和便民寄存点，采用SPSS统计分析软件，运用k-均值聚类分析方法，将42个便民寄存点按照空间聚类分为7个区域，选择每个区域的聚类中心（或离聚类中心最近的点）作为末端配送站点位置。表4为末端配送站点选址及分配方案，图4为末端配送站点选址结果。

3.3 算例结果分析

由表3、表4、图3、图4可得，区域内105个居民小区由4个快递分拨中心，7个末端配送站点，42个便民寄存点负责M市快递配送业务，便民寄存点与各居民小区中心点之间的距离不超过3 km。选址结果图表明节点选址均匀，与居民小区距离合理。分配方案根据各自设施能力（便民寄存点服务半径约束）及周边居民小区需求紧迫性，已达成优化分配目的。选址及快递量分配方案较合理，可有效降低快递企业成本、提高配送效率、便于配送业务管理。算例结果表明本文所建立的模型符合实际，具

4 结束语

本文研究了考虑双层配送模式的城市快递配送网络的构成及其优势，从系统的角度对城市快递双层配送网络进行了阐述。

本文建立了城市快递双层配送网络的二级节点选址模型，提出分解算法求解模型。首先采用改进的最少点覆盖启发式算法进行便民寄存点选址;其次在便民寄存点选址的基础上，采用k-均值聚类算法进行末端配送站点选址;最后通过算例进行模型和算法验证，应用MATLAB编程实现了便民寄存点选址，应用SPSS软件实现了末端配送站点选址。算例结果表明本文所提出的数学模型符合实际，所提出的分解算法能够在较短时间内求解得到合理的解，具有一定的实用价值。

参考文献：

[1]张哲辉. 快递企业国内服务网点布局研究[D]. 大连：大连海事大学， 2005.

[2]张兰. 快递企业网点布局研究[D]. 长沙：中南大学， 2008.

[3]焦艳. 城市电子商务物流网络优化设计与系统实现[D]. 上海：上海交通大学， 2013.

[4]丛迪悦. 快递企业服务网点布局优化研究[D]. 大连：大连海事大学， 2014.

[5]杨从平， 郑世珏， 党永杰， 等. 基于配送时间及节点流量约束的快递网络优化[J]. 系统工程， 2015， 33（11）：53-59.

[6]卢文涛. 基于时间阈值的区域快递网络优化[J]. 温州大学学报（自然科学版）， 2016， 37（2）：46-54.

[7]程赐胜， 蒲云虎， 高慧. 基于离散粒子群算法的城市物流节点选址模型[J]. 长沙理工大学学报（自然科学版）， 2008， 5（2）：20-24.

（编辑 贾裙平）