采用改进模拟植物生长算法的世界石油船队总运力预测

王诺 丁凯 吴迪

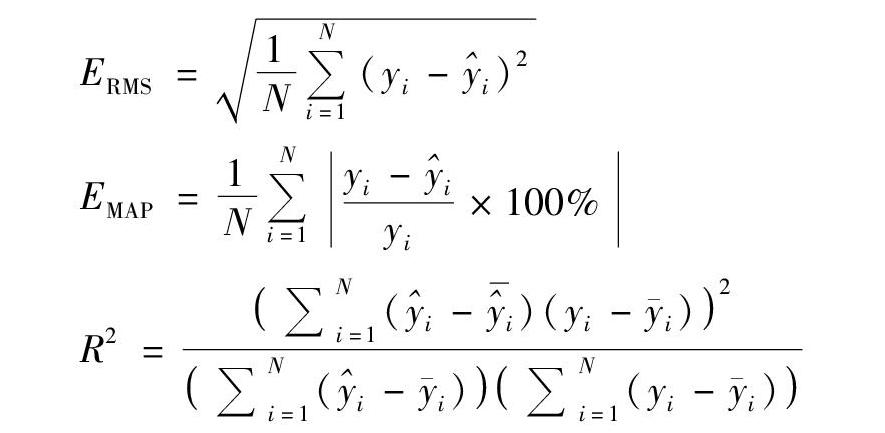
摘要：为准确预测世界石油船队总运力情况，收集近15年来世界石油船队总运力的统计数据，分别从总运力趋势波动和运力净增量波动两个方面进行分析。建立时间序列模型来揭示世界石油船队总运力的变化规律，用改进的模拟植物生长算法（plant growth simulation algorithm，PGSA）进行求解。与遗传算法进行对比，改进算法的程序运行时间、均方根误差和平均绝对百分比误差均较低，算法预测的结果与历史数据的拟合度达92.32%，预测结果具有较高的准确性。分析思路和方法可为航运企业科学决策提供技术支撑。

关键词：世界石油船队; 总运力预测; 净增量; 时间序列模型; 模拟植物生长算法（PGSA）

中图分类号：U699

文献标志码：A

Abstract：In order to accurately predict the total transport capacity of world crude oil fleets， the data of total transport capacity of world crude oil fleets over the past 15 years are collected， and the data are analyzed from two aspects：the fluctuation of the total transport capacity trend and the fluctuation of the net increment of transport capacity. The time series model is established to reveal the change rule of the total transport capacity of world crude oil fleets， and the improved plant growth simulation algorithm （PGSA） is used to solve the model. Compared with the genetic algorithm， the program running time， the root mean square error and the mean absolute percent error of the improved PGSA are lower. The fitting degree between the predicted data obtained by the improved PGSA and the historical data is 92.32%. The prediction results are of high accuracy. The analysis idea and method can provide technical support for scientific decision-making of shipping enterprises.

Key words：world crude oil fleet; prediction of total transport capacity; net increment; time series model; plant growth simulation algorithm （PGSA）

收稿日期：2018-06-03

修回日期：2018-09-26

基金項目：国家自然科学基金（71372087）;国家海洋软科学项目（JJYX201612-1）

作者简介：

王诺（1954—），男，辽宁大连人，教授，博导，博士，研究方向为交通运输规划与管理、物流工程与管理，（E-mail）wangnuodl@126.com

0 引 言

目前我国已成为能源消耗和石油进口大国，据英国石油公司（British Petroleum，BP）发布的《世界能源展望（2016年版）》预测：到2035年，我国能源消耗量将占全球能源消耗总量的25%，石油进口依赖度将从当前的64%上升至76%。我国石油进口主要依赖海上运输，世界石油船队总运力的变化将直接影响石油航运市场行情，导致石油船队运输成本产生波动。因此，准确预测世界石油船队总运力的变化趋势，对于调整我国船队规模，稳定石油航运市场，制定相关发展规划，具有重要的意义。

航运市场相关因素复杂多变，如何对其进行预测一直是航运研究的热点和难点。在船舶运力预测方面：王顺娟[1]总结了海运量的变化规律，结合现状预测市场未来的需求量，采用灰色预测法对未来干散货海运量进行了定量预测;刘海青[2]根据货物周转量数据进行二次回归曲线拟合，测算了船舶运力的配置;陈言诚等[3]采用系统动力学方法构建了船舶运力模型，提供了模拟分析航运市场的方法;李志等[4]利用模糊神经推理系统，以历年世界散货船队总吨位等数据建立了预测模型。相对于普通货物，油品是一种批量大、装卸工艺相对简单、适合整船运输的特殊货种。在油船运输市场和石油船队运力预测研究方面：刘妍[5]针对21世纪初期油船运输市场的发展情况，发现不同吨位油船的运力和数量均有不同幅度的增加，且油船趋向于大型化;尹栋[6]从国际油船运输市场入手，对国际油船运输市场的供给、需求以及船舶的数量、运力等进行了分析;邹葵等[7-8]回顾了全球油船运输市场运力的发展，对油船运输市场进行了分析和预测。

上述研究均是以船舶运力为研究对象构建模型的，虽然能够对运力的发展状况进行判断，在一定程度上揭示国际航运市场的基本发展趋势，但因各种影响因素复杂多变，预测精度不够理想，预测方法很难在实际中得到应用和推广。为提高预测的精度，本文将世界石油船队总运力的变化情况分解为总运力趋势波动和运力净增量波动两个方面分别进行分析，以各年度船舶运力净增量为研究对象，首先根据运力净增量所呈现的周期性波动特点建立时间序列模型，对模拟植物生长算法（plant growth simulation algorithm，PGSA）进行改进并用于求解模型，然后采取将逐年净增量累加并与初始基准年总运力值求和的方法得到世界石油船队历年总运力的预测值，最后通过对比分析实际数据与预测值，证明本文预测模型和算法的适用性和有效性。

1 问题描述与建模

1.1 问题描述

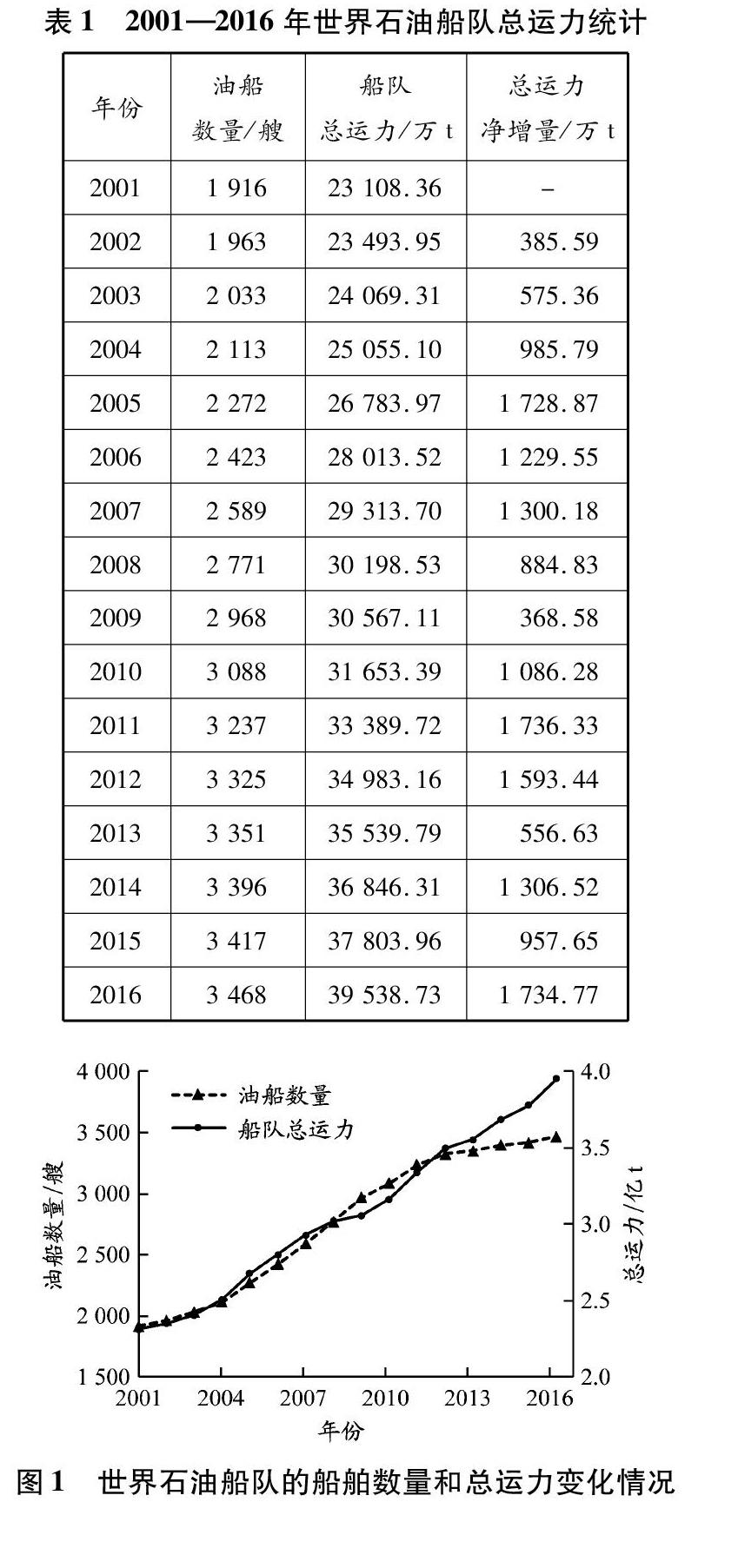
据克拉克森（Clarkson）情报网对运力大于7万t的油船的统计：2001年世界石油船队总运力为23 108.36万t，2016年的为39 538.73万t，比2001年的增长了近1倍;油船數量由2001年的1 916艘增长到2016年的3 468艘，增加了近1倍。2001—2016年世界石油船队总运力统计结果见表1。受2008年金融危机影响，石油生产和消耗出现增速减缓趋势，航运业呈现萎靡状态，船舶运力净增量出现下降趋势，船舶数量和总运力增长速度虽然较慢[9]，但整体上仍处于上升状态，见图1。从总体来看，2001—2016年世界石油船队运力净增量呈现一定的周期性变化趋势，见图2。

由图1和2可知：（1）世界石油船队总运力的变化具有一定的平稳性特点，总的趋势为缓慢上升。事实上，在全球经济一体化的推动下，世界经济总体上保持持续增长态势，这种态势决定了世界石油船队总运力将长期呈现平缓增长趋势。（2）世界石油船队运力净增量变化十分活跃，呈现出显著的周期性波动。从全球范围来看，航运领域基本已经完全市场化，世界石油船队运力净增量变化服从市场周期性变化规律，市场需求的变化推动着运力市场的变化，世界石油船队运力净增量也会出现周期性变化。

从数量级的角度分析可以发现，由于世界石油船队总运力的数量级较大，而年度运力净增量的数量级较小，如果直接对世界石油船队总运力在总体上进行预测，其误差很可能淹没数量级较小的运力净增量，导致准确性降低，而采取将世界石油船队总运力变化分解为总运力趋势波动和运力净增量波动两个方面进行分析，便可以避免产生这一问题。

1.2 模型构建

首先，将世界石油船队总运力与年度运力净增量进行分解;然后，在总运力初始值的基础上，对历年运力净增量进行累加，采用时间序列模型揭示其变化规律;最后，将各年度总运力预测净增量的累加值与初始基准年总运力相加，得到总运力预测值。

设第t年的总运力预测值为Ft，建立世界石油船队总运力预测模型：

式中：F0为初始基准年总运力;gi为年度运力净增量预测函数。

通过对世界石油船队运力净增量变化曲线的形态分析，发现其周期性波动与三角函数变化特征较为相似，因此初选三角函数对年度运力净增量进行描述：

式中：j为净增量变化幅度;k、l、m为三角函数内的一元二次函数系数;n决定三角函数基准轴位置。

设Δht为第t年船队总运力实际净增量ht与预测净增量偏差的绝对值，则

综上，模型的目标函数为

G1为第1年实际净增量与预测净增量的最小偏差值，G2为前2年实际净增量与预测净增量最小偏差值的累加值，其他以此类推。

2 求解算法

在算法研究方面：李彤等[10-11]首先提出了PGSA，用于求解设施选址、电力系统优化等领域的整数规划问题;王婷婷等[12]将PGSA应用于整数优化调度问题，证明了该方法的有效性和可行性;RAO等[13]将PGSA用于求解电容器的优化布置。分析发现，上述关于PGSA的应用均是针对整数规划的研究，但本文研究的是非整数规划问题，需要将算法中的生长步长规则改为非整数的任意步长，但调整后又会产生计算收敛速度较慢、求解精确度较低等问题。为此，通过引入二进制规则改进PGSA，以便在求解非整数规划问题时有效提高算法的搜索能力和求解精度。

2.1 PGSA特点

在算法原理上，根据植物多个枝、节点组成的生长系统沿着易获得光的方向生长的结构特点，将这一生长过程具体描述为：①茎秆发芽生长，在一些生长节点的部位长出新枝;②在旧枝上也会长出新枝;③植物最终由相似的结构组成，并朝着最易获得光的方向生长[14]。图3为植物生长形态变化模拟图。

根据以上基本原理，将植物生长空间对应为计算可行域，建立植物枝芽始终朝向最易获得光的方向生长的仿生模型，模拟植物生长的整个过程。当植物某一枝干上有多个节点时，根据形态素的浓度状况选择长出新枝的最佳位置，在形态素浓度值较大的节点上生长出新枝的概率会更大，而植物形态素的浓度通常由节点所处的环境状况决定。随着枝干的生长，节点数不断增加，每当新1轮新枝生长时形态素浓度将在各生长点之间进行重新分配，计算公式如下：

式中：P（z）γ为十进制下第z+1轮新枝生长时第γ个生长点的形态素浓度;f（ΔX（0））为十进制下初始生长点的目标函数值;f（ΔX（z）γ）为十进制下第z+1轮新枝生长时第γ个生长点的目标函数值;α表示十进制下第z+1轮新枝生长时生长点的个数。

2.2 PGSA改进

2.2.1 基本思路

为有效求解非整数规划问题，本文对算法规则进行如下改进：①采用二进制对参数进行编码，以二进制可行域作为求解非整数规划的解空间;②将十进制下生长点转换为二进制下生长点后，以二进制生长方式（若原生长点中共有n位基因，则以每一位基因分别转向逻辑相反方向的方式产生新的生长点，即1转变为0，0转变为1。例如，101可转变为001、111和100）模拟植物生长过程，在计算形态素浓度时，将二进制下生长点转换为十进制下生长点进行计算。

2.2.2 基本步骤

步骤1 选定初始生长点ΔX（0）=（Δx（0）1，Δx（0）2，…，Δx（0）n），初定迭代最优解X′min（0）=ΔX（0），迭代最优值F′min（0）=F（ΔX（0）），确定最大生长循环次数λ、解的维数w和每一维解的编码位数v。

步骤2 将十进制下生长点ΔX（z）（z=0，1，…，k，初始生长时z=0，以后每生长1次z值加1，下同）编码为二进制下生长点A（z），以二进制生长方式生成新生长点集合。

步骤3 将二进制下生长点的集合解码为十进制下生长点的集合φ，求解十进制下生长点集合中各生长点的目标函数，淘汰劣于初始基点目标函数的生长点，同时更新生长点的集合，得出生长点集合中的最优解X′min和最优值F′min。

步骤4 利用式（3）计算十进制下生长点集合φ中各生长点出现的概率。

步骤5 基于步骤4得到的各新生长点出现的概率，形成各生长点出现概率的[0，1]空间，由随机数落于[0，1]概率空间内的位置决定下一生长循环的生长点ΔX（z+1）。

步骤6 重复以上循环过程，如连续未更新最优解的生长次数达到设定值η或生长循环次数达到设定值λ，则输出最优解Xmin=X′min，输出最优值Fmin=F′min，算法结束，否则转至步骤3重新计算。

3 模拟计算与结果分析

设定实验组初始生长点ΔX（0）=（700，0.025，1，-3，1 000），生长点最大循环次数为3 000次，当连续未更新最优解的生长次数为1 000时计算停止，每一维解的编码位数设定为10。为验证算法参数设定的有效性与合理性，设定对照组的生长点最大循环次数为2 000次，当连续未更新最优解的生长次数为800时计算停止，每一维解的编码位数设定为5，分别运行程序，并对结果进行对比分析。

3.1 计算结果

采用MATLAB 2014a编写程序，其配置为Windows 7，Intel（R）Core（TM）i3-2100 CPU @ 3.70 GHz 4 GB。实验组程序运行了19.32 s，在迭代1 061次后结束;对照组程序运行了21.61 s，在迭代1 159次后结束。得到的最优值Fmin=2 869.92，最优解Xmin=（749.76，  0.024 9， 0.799 1， -3.001， 1 049.36），由此可知在得到相同的最优解和最优值的前提下，实验组的运行时间更短，迭代次数更少。算法迭代收敛情况见图4。由图4可知，随着迭代次数的增加，最优值整体呈现逐渐降低趋势。此外，对照组在开始阶段的最优值均高于实验组，迭代1 000次后出现最优值骤降的现象，整体效果劣于实验组。将实验组的各个参数代入式（2），得出世界石油船队年度运力净增量预测模型为

根据年度运力净增量预测模型，得出世界石油船队总运力预测模型为

3.2 凈增量拟合

为验证改进算法的有效性和适用性，与用遗传算法预测的结果进行对比。将2001—2016年石油船队总运力的实际净增量与预测净增量进行拟合。由图5可知，大部分散点贴近实曲线，两者拟合度达到92.32%。拟合程度较好表明该模型能较好地反映世界石油船队运力净增量的波动，可用于对世界石油船队运力净增量的预测。

3.3 算法结果对比

将用遗传算法计算出的各个参数代入式（1），结合改进算法计算石油船队总运力预测值的误差，计算结果见表2。分析表2可知：改进算法预测值最大相对误差为3.95%，平均相对误差为1.55%;遗传算法预测值最大相对误差为5.21%，平均相对

误差为2.56%。由此可知，改进算法预测值的有效性和准确性比遗传算法的高。

3.4 性能准则

将遗传算法与改进算法从程序运行时间、算法计算结果准确性两个方面分别进行比较。将均方根误差（ERMS）、平均绝对百分比误差（EMAP）、拟合效果评价系数R2作为算法预测准确性的评价指标，其中ERMS反映的是样本的离散程度和预测精度，EMAP反映的是预测值与实际值的接近水平，ERMS和EMAP的值越小表示预测的准确性越高，拟合效果评价系数R2越大说明预测模型越合理[15]。预测准确性指标定义如下：

式中：N为预测样本数;yi为实际值;i为算法预测值;i和i分别为i和yi的均值。

模拟和对比实验均在计算机上运行，各计算10次，算法对比结果见表3。结果显示，改进算法在各项指标上均有改进，其中：运行时间减少了24.64%;ERMS值为641.76，低于遗传算法计算所得值（980.72）;EMAP值为1.55%，低于遗传算法计算所得值（2.41%）;改进算法预测值与实际值两者的拟合度为0.984 6，遗传算法预测值与实际值两者的拟合度为0.905 3，表明改进算法预测结果比遗传算法预测结果更接近实际值。

3.5 预测结果

根据上文所建模型计算出预测值，将预测值与实际值进行拟合，具体情况见图6。用本文所建模型预测世界石油船队2017—2021年的总运力，结果分别为3.925亿t、3.964亿t、4.111亿t、4.271亿t和4.315亿t。

4 结 论

本文主要对世界石油船队总运力增长趋势的预测开展研究，通过统计近15年的有关数据，将其分解为总运力趋势波动和运力净增量波动两个方面进行分析，建立时间序列模型来揭示世界石油船队总运力的变化规律。利用改进的模拟植物生长算法（PGSA）进行求解，将改进算法预测结果与遗传算法预测结果进行对比，结果显示改进算法具有更高的准确性。以本文算法预测的世界石油船队总运力的增长趋势与历史数据拟合度达到92.32%，预测结果具有较高的可靠性。本文模型和算法能较好地对未来世界石油船队总运力做出准确预测，其分析思路和方法有助于分析石油航运市场的动态变化情况，可为航运企业的科学决策提供技术支撑。本文算法在有些方面还有待于提高，如需要迭代1 000次以上才能寻找到全局最优解，因此在保证顺利得到最优解的前提下，降低迭代次数是下一步研究的方向。

参考文献：

[1]王顺娟. 世界干散货航运市场运量及运力分析[J]. 综合运输， 2009（5）：65-68.

[2]刘海青. 长江干线液货危险品船舶运力预测与调控建议[J]. 中国水运， 2012（8）：28-29. DOI：10.13646/j.cnki.42-1395/u.2012.08.012.

[3]陈言诚， 林国龙， 胡志华. 基于系统动力学的干散货航运市场运力供给研究[J]. 武汉理工大学学报（交通科学与工程版）， 2012， 36（4）：799-803. DOI：10.3963/j.issn2095-3844.2012.04.034.

[4]李志， 邵哲平， 邹开其， 等. 利用模糊神经推理系统ANFIS预测世界散货船队运力[C]//中国系统工程学会.模糊集理论与模糊应用专辑：中国系统工程学会模糊数学与模糊系统委员会第十届年会论文选集. 中国系统工程学会， 2000.

[5]刘妍. 国际油船运输市场发展研究[J]. 中国水运， 2007， 5（6）：6-7.

[6]尹栋. 国际油船运输市场的周期波动及预测[D]. 大连：大连海事大学， 2013.

[7]邹葵. 2012年国际油船运输市场回顾与2013年展望[J]. 世界海运， 2013， 36（2）：5-10.

[8]邹葵， 孙琦. 国际油船运输市场2015年回顾与2016年展望[J]. 世界海运， 2016， 39（3）：8-14.

[9]LAULAJAINEN R. Operative strategy in tanker （dirty） shipping[J]. Maritime Policy and Management， 2008， 35（3）：313-339. DOI：10.1080/03088830802080522.

[10]李彤， 王春峰， 王文波， 等. 求解整数规划的一种仿生类全局优化算法：模拟植物生长算法[J]. 系统工程理论与实践， 2005， 25（1）：76-85.

[11]李彤， 陈畴镛. 求解非线性二层规划问题的模拟植物生长算法[J]. 中国管理科学， 2012， 20（4）：160-166.

[12]王婷婷， 杨琴. 基于模拟植物生长算法的超市收银口优化调度[J].计算机应用， 2014， 34（5）：1516-1520. DOI：10.11772/j.issn.1001-9081.2014.05.1516.

[13]RAO R S，NARASIMHAM S V L， RAMALINGARAJU M. Optimal capacitor placement in a radial distribution system using plant growth simulation algorithm[J]. Electrical Power & Energy Systems， 2011， 33（5）：1133-1139. DOI：10.1016/j.ijepes.2010.11.021.

[14]TANG Chengpei， LIU Ruiqi， NI Jiangqun. A novel wireless sensor network localization approach：localization based on plant growth simulation algorithm[J]. Elektronika Ir Elektrotechnika， 2013， 19（8）：97-100. DOI：10.5755/j01.eee.19.8.5326.

[15]周飛， 吕一清， 石琳娜. 改进粒子群算法优化灰色神经网络预测模型及其应用[J]. 统计与决策， 2017（11）：66-70. DOI：10.13546/j.cnki.tjyjc.2017.11.017.

（编辑 贾裙平）