基于因子分析和曲线拟合的集装箱吞吐量预测

贾飞跃 韩晓龙

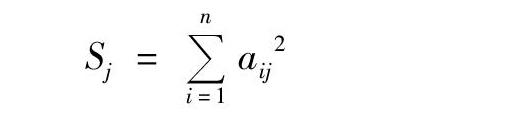
摘要：为提高集装箱吞吐量的预测精度，提出基于因子分析和曲线拟合的集装箱吞吐量预测模型。以上海港为例，通过因子分析，分析影响集装箱吞吐量的主要因素，筛选出主因子，得到不同年份的综合经济发展值;再运用曲线拟合方法，建立以综合经济发展值为自变量，以集装箱吞吐量为因变量的三次曲线模型;运用自回归积分移动平均（autoregressive integrated moving average， ARIMA）模型预测2016—2020年的综合经济发展值，进而求得2016—2020年上海港集装箱吞吐量预测值。结果表明：该模型的拟合效果和预测精度均较高，可以运用到集装箱吞吐量预测中。给出上海港在国内经济新常态下转型升级的建议。

关键词：自回归积分移动平均（autoregressive integrated moving average， ARIMA）模型; 因子分析; 曲线拟合; 集装箱吞吐量预测

中图分类号：U691.71

文献标志码：A

收稿日期：2018-06-02

修回日期：2018-08-20

基金项目：国家自然科学基金（71471110）;上海市科学技术委员会创新项目（16DZ1201402，16040501500）;上海市科学技术委员会工程中心能力提升项目（14DZ2280200）;上海海事大学研究生学术新人培育计划（YXR2017014）

作者简介：

贾飞跃（1994—），男，河南开封人，硕士研究生，研究方向为物流工程与管理，（E-mail）1761262763@qq.com

韩晓龙（1978—），男，山东潍坊人，副教授，硕导，博士，研究方向为物流与供应链管理，（E-mail）xlhan@shmtu.edu.cn

Abstract：In order to improve the prediction accuracy of container throughput， a container throughput prodiction model based on factor analysis and curve fitting is proposed. Shanghai Port is taken as an example. Through factor analysis， the main factors affecting the container throughput are analyzed， the principal component factors are selected， and the comprehensive economic development values of different years are obtained; a curve fitting method is used to establish a cubic curve model， where the comprehensive economic development value is taken as an independent variable and the container throughput is taken as a dependent variable; the comprehensive economic development values of 2016-2020 are predicted by the autoregressive integrated moving average （ARIMA） model， thus the predicted values of the container throughput of Shanghai Port in 2016-2020 are obtained. The results show that the fitting effect and the prediction accuracy of the model are both high and can be applied to the container throughput prediction. The suggestions of the transformation and upgrading of Shanghai Port under the new normal of Chinese economy are given.

Key words：autoregressive integrated moving average （ARIMA） model; factor analysis; curve fitting; container throughput prediction

0 引 言

隨着国际贸易的发展，世界各港口之间的竞争正逐步演变为以集装箱吞吐量为核心的港口综合实力的竞争，而集装箱吞吐量的精准预测是合理规划港口码头的重要基础。

江舰等[1]利用近年来的相关数据对港口集装箱吞吐量、港口所在城市的国民生产总值以及地方进出口商品总值进行了计量经济分析，通过二元线性回归模型对港口未来集装箱吞吐量进行预测，并对模型进行了相关检验。朱小檬等[2]采用时间序列-因果关系结合法，把国内生产总值（GDP）作为解释变量，利用多项式回归模型拟合集装箱吞吐量序列，形成GDP时间序列对集装箱吞吐量序列的因果关系。王文[3]采用季节性复合序列分解方法，得到通过季节指数分离的序列数据的回归模型，用来预测未来两年外贸吞吐量，并由它与箱量间的线性关系得到相对应的集装箱吞吐量预测值，预测效果显著。杨金花等[4]根据上海港集装箱码头的具体情况计算其通过能力，通过产能利用率指标得出上海港集装箱码头不存在产能过剩的结论，并提出了在现有码头设施条件下提高产能的建议。陈昌源等[5]引入弱化算子理论对GM（1，1）模型原始数据进行预处理，分别应用传统模型和改进GM（1，1）模型对上海港集装箱吞吐量进行预测，比较两种模型的预测精度及曲线拟合度。崔巍等[6]通过对历年内河集装箱吞吐量的统计与分析，采用三次指数平滑法建立预测模型，对珠江内河集装箱吞吐量进行了分析和预测。

目前，预测集装箱吞吐量的方法很多，如线性回归法、指数平滑法[6-7]、人工神经网络法[8-9]、灰色预测法[10-11]等，其中：线性回归法不能根据数据的差异进行灵活调整，预测精度往往不高;指数平滑法的平滑次数和平滑系数的确定相对困难;人工神经网络法存在收敛速度慢、对数据质量要求高等问题;灰色预测法需要原始序列呈现非负指数增长趋势，而所研究的原始序列有时无法满足该条件。为此，本文提出基于因子分析和曲线拟合的集装箱吞吐量预测模型，即首先确定影响集装箱吞吐量的主要影响因素，并通过因子分析消除因素间的多重共线性，然后得到各年份的综合经济发展值，最后对综合经济发展值与集装箱吞吐量进行曲线拟合，找出最佳预测模型，从而对集装箱吞吐量作出预测并进行检验。

1 预测模型建立步骤

基于因子分析和曲线拟合的集装箱吞吐量预测模型的建立步骤[12]如下：

步骤1 对问题进行分析，收集数据，并选取影响集装箱吞吐量的指标。

步骤2 判断指标矩阵是否适合进行因子分析。通常采取相关系数矩阵计算、KMO检验和Bartlett球度检验来进行判断。若适合，则转到步骤3，否则转到步骤1。

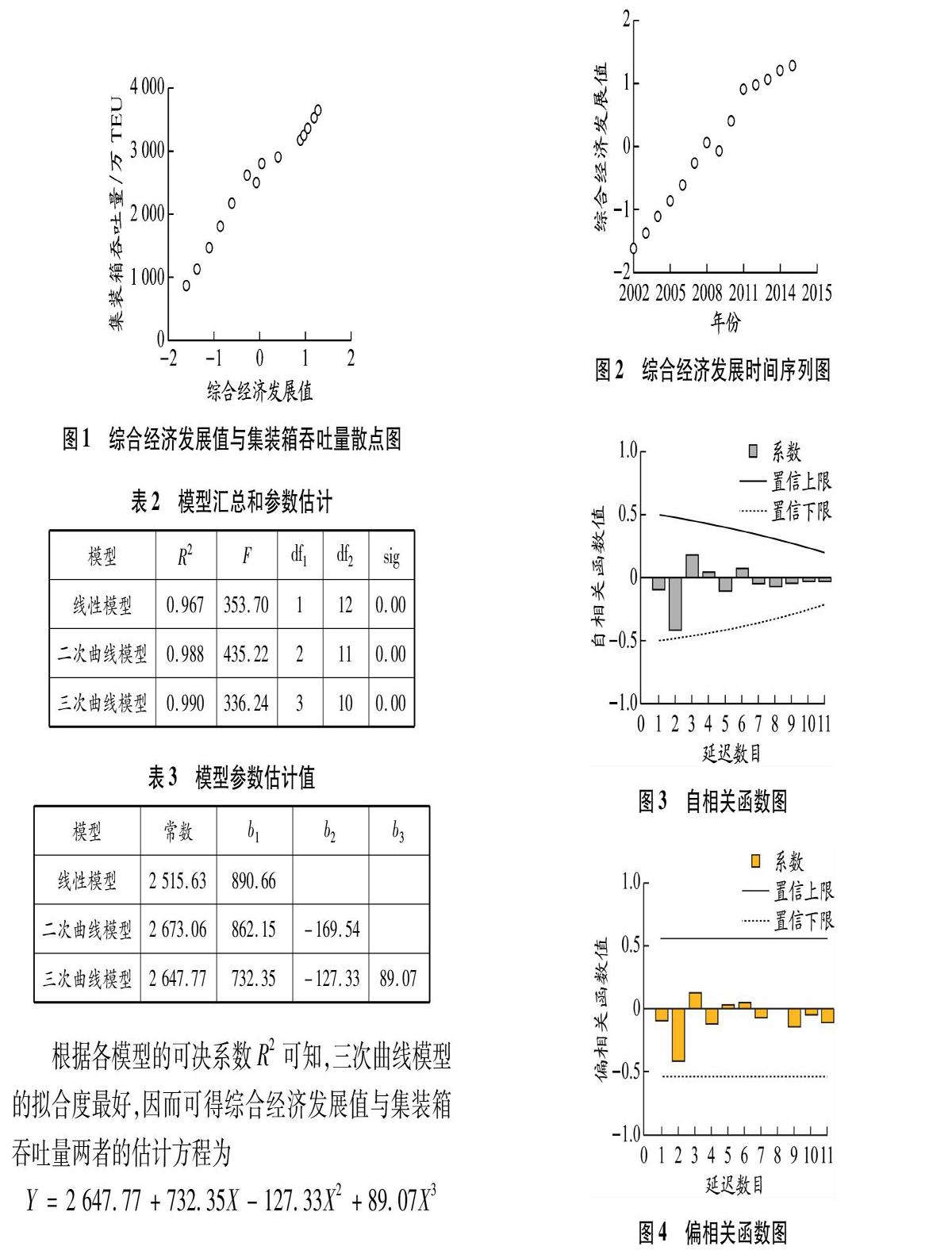
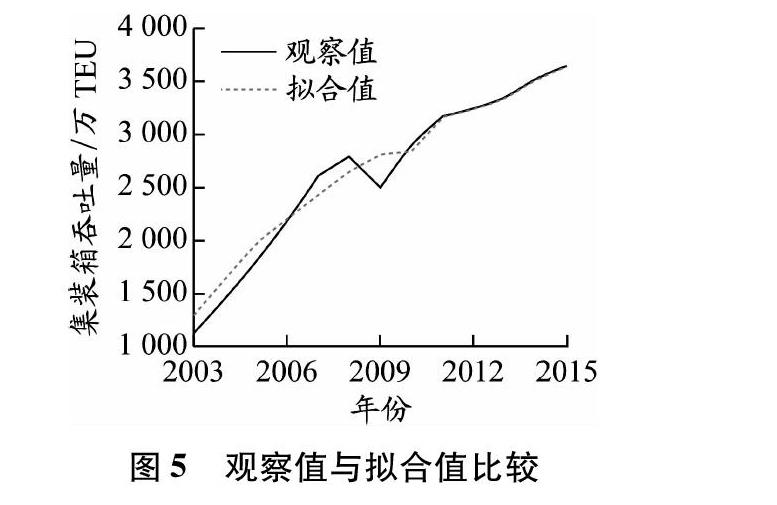
步骤3 确定主因子。设x1，x2，…，xn为n个影响因素，当前k（k

式中：λi为主因子的方差占总方差的比例。

步骤4 若k个主因子无法确定或实际含义不很明显，则需将因子进行旋转以获得较为明显的实际含义。把n个原始变量表达为k个主因子的线性组合。要寻找的前k个主因子记为E1，E2，…，Ek，依据主因子与原始变量之间的关系建立因子分析数学模型：

式中：aij表示第i个变量与第j个主因子之间的线性相关系数。这个模型表示成矩阵形式为

式中：E为主因子向量，E1，E2，…，Ek可以理解为高维空间中相互垂直的k个坐标轴;A为因子载荷矩阵;ε为特殊因子向量。

步骤5 确定综合经济发展值（亦称为综合因子得分）。以主因子的方差贡献率为权重，由各主因子的线性组合得到主因子得分函数，进而确定各主因子的综合经济发展值。主因子的方差贡献率权重为

其值越高，说明主因子的重要程度越高。

步骤6 运用曲线拟合方法对综合经济发展值与集装箱吞吐量进行曲线拟合，找出最佳预测模型。

步骤7 运用自回归积分移动平均（autoregressive integrated moving average， ARIMA）模型预测未来时期综合经济发展值，然后将其代入最佳预测模型中预测未来集装箱吞吐量。

2 实证分析

2.1 数据收集及指标选取

为评价基于因子分析和曲线拟合的集装箱吞吐量预测模型的拟合效果和预测精度，选取上海港作为研究对象。影响上海港集装箱吞吐量Y的因素很多，鉴于数据可得性，选取地区生产总值X1、进出口总额X2、工业总产值X3、货物运输量X4和社会消费品零售总额X5等5个指标作为集装箱吞吐量的影响因素。采用2002—2015年上海港集装箱吞吐量及其影响因素数据（见表1）进行实证研究。

通过对上海港集装箱吞吐量影响因素的相关性分析可知，指标间存在高度线性相关性，同时Bartlett球度检验统计量观测值为171.508，KMO值为0.782，均通过检验，因而所建指标矩阵适合进行因子分析。

2.2 因子分析

运用SPSS软件进行因子分析[13]，可得以下结论：（1）在提取主因子时，地区生产总值、进出口总额、工业总产值、货物运输量和社会消费品零售总

额的共同度分别为0.977、0.992、0.977、0.950和0.936，因子载荷值分别为0.988、0.996、0.989、0.975和0.967，同时所提取的主因子的特征根为4.833，并且能够解释5个指标总方差的96.65%，因此此次提取主因子的效果较好。

（2）各主因子得分系数分别为0.205、0.206、0.205、0.202和0.200，从而可得2002—2015年综合经济发展值分别为-1.61、-1.37、-1.10、-0.86、-0.61、-0.26、0.06、-0.07、0.41、0.90、0.98、1.06、1.20和1.28。

2.3 曲线拟合

在上面的因子分析中得到的不同年份的综合因子得分反映了不同年份的综合经济发展值，于是可以利用综合因子得分预测未来上海港集装箱吞吐量。通过绘制以综合经济发展值X为横坐标、以上海港集装箱吞吐量Y为纵坐标的散点图（见图1），可以初步判断两者间存在的函数模型有线性模型、二次曲线模型和三次曲线模型。利用SPSS软件的曲线拟合功能，评估这3个模型对综合经济发展值与集装箱吞吐量两者的拟合效果，具体见表2和3，其中R2为可决系数，F为特征值，df1、df2表示模型自由度（degree of freedom），sig表示显著性，b1、b2、b3分别表示曲线的一次项、二次项和三次项系数。

根据各模型的可决系数R2可知，三次曲线模型的拟合度最好，因而可得综合经济发展值与集装箱吞吐量两者的估计方程为

2.4 运用ARIMA模型预测综合经濟发展值

首先，绘制综合经济发展时间序列图，见图2。由图2可知，2002—2015年间综合经济发展时间序列总体呈现波动式上升，即该序列处于非平稳状态。由于样本数据存在上升态势，为消除样本数据可能存在的异方差现象，需要进行差分处理。经过一阶差分后序列趋于平稳，其自相关性和偏相关性如图3和4所示：一阶差分序列的自相关函数值和偏相关函数值在其二阶差分值达到峰值后都呈现出拖尾衰减特性。由此可以认为，一阶差分时间序列为平稳的白噪声序列，从而可以构建ARIMA（2，1，2）模型。该模型的可决系数R2为0.983，标准化BIC为-2.502，因而可以认为该模型的拟合效果相对较好。用该模型预测的2016—2020年上海港集装箱吞吐量的综合经济发展值分别为1.501 91、1.692 35、1.785 82、1.884 16和1.993 02。

2.5 三次曲线模型拟合效果检验

运用ARIMA（2，1，2）模型，求出2003—2015年综合经济发展值，然后将其代入三次曲线模型中可

得2003—2015年上海港集装箱吞吐量拟合值，将其与2003—2015年的观察值进行比较，可求出观察值与拟合值的平均绝对误差仅为5.04%，其具体拟合效果见图5。从图5可以看出，2012—2015年集装箱吞吐量拟合误差率趋于0，因而可以认为模型拟合效果非常好，用该模型得到的2016—2020年上海港集装箱吞吐量预测结果可以认为是较为精确的。

2.6 预测集装箱吞吐量

预计“十三五”期间全国港口吞吐量增长速度可能会低于国民经济发展速度，我国港口在今后一段时期内总体上会处于平稳发展的阶段，即我国港口货物吞吐量和集装箱吞吐量增长将进入中低速增长的“常态”[14]。将2016—2020年综合经济发展的预测值代入三次曲线模型中，可求得上海港集装箱吞吐量预测值分别为3 762.2万、3 954.2万、4 056.8万、4 171.4万、4 306.7万TEU。2016和2017年上海港集装箱吞吐量预测值与观察值（分别为3 713.3万和4 030.0万TEU）相比，其绝对误差分别为1.32%和1.88%。根据预测结果分析可知，在“十三五”

期间上海港集装箱吞吐量仍将呈现平稳增长态势，且2016—2020年的环比增长率分别为3.21%、5.10%、2.60%、2.82%、3.24%。由此可知，年平均增长率为3.40%，符合我国港口在“十三五”期间集装箱吞吐量增长进入中低速增长的“常态”。

3 结束语

基于因子分析和曲线拟合对上海港集装箱吞吐量进行预测，得出以下结论：

第一，在确定影响集装箱吞吐量主要因素的基础上，通过因子分析确定主因子，进而求得各年份的综合经济发展值，然后通过对综合经济发展值与集装箱吞吐量进行曲线拟合找出最佳预测模型，从而可建立基于因子分析和曲线拟合的集装箱吞吐量预测模型。结果表明：该模型的拟合效果好，预测精度高，可以运用到集装箱吞吐量预测中。

第二，上海港集装箱吞吐量在平稳增长的同时其增速将明显放缓。因此，面对中国经济的新常态和国际贸易形势的复杂性，上海港作为一个国际航运枢纽，在提升港口硬件实力的同时，更需注重提升自身软实力。借助“一带一路”和“海运强国”的发展契机，上海港应积极实现港口专业化和集约化经营的转型升级，深化完善“两型”港口建设，提升上海港核心竞争力。对于我国集装箱港口而言，集装箱港口企业一定要延伸物流服务，在做大做强港口主业的基础上，加强港口与区域内产业互动，积极发展临港工业服务功能，进一步服务腹地经济产业链，增加港口服务价值。

参考文献：

[1]江舰， 王海燕， 杨赞. 集装箱吞吐量及主要影响因素的计量经济分析[J]. 大连海事大学学报， 2007， 33（1）：83-86.

[2]朱小檬， 栾维新， 朱义胜. 基于时间序列-因果关系结合法的中国海港集装箱吞吐量中长期预测[J]. 大连海事大学学报（社会科学版）， 2014， 13（5）：1-5.

[3]王文. 线性回归结合季节性复合序列的深圳港集装箱吞吐量预测[J]. 中国水运， 2012， 12（12）：23-25， 27.

[4]杨金花， 杨艺. 基于灰色模型的上海港集装箱吞吐量预测[J]. 上海海事大学学报， 2014， 35（2）：28-32.

[5]陈昌源， 戴冉， 杨婷婷， 等. 基于改进GM（1，1）模型的上海港集装箱吞吐量预测[J]. 船海工程， 2016， 45（4）：153-156.

[6]崔巍， 叶佳. 基于三次指数平滑的珠江内河集装箱吞吐量预测[J]. 珠江水运， 2011（12）：112-114.

[7]关克平， 齐梦雅. 基于指数平滑法的宁波舟山港港口吞吐量预测研究[J]. 中国水运， 2013， 13（12）：28-29.

[8]范莹莹， 余思勤. 基于NARX神经网络的港口集装箱吞吐量预测[J]. 上海海事大学学报， 2015， 36（4）：1-5.DOI：10.13340/j.jsmu.2015.04.001.

[9]刘长俭， 张庆年. 基于时间序列BP神经网络的集装箱吞吐量动态预测[J]. 水运工程， 2007（1）：4-11.

[10]王再明， 王宏波. 灰色系统理论在港口吞吐量预测中的應用[J]. 武汉理工大学学报（交通科学与工程版）， 2005， 29（3）：456-459.

[11]陈秀瑛， 古浩. 灰色线性回归模型在港口吞吐量预测中的应用[J]. 水运工程， 2010（5）：89-92.

[12]徐国祥. 统计预测和决策[M]. 上海：上海财经大学出版社， 2006：202-216.

[13]王璐， 王沁. SPSS统计分析基础、应用与实战精粹[M]. 北京：化学工业出版社， 2012：230-256.

[14]陈羽. 2015年我国港口集装箱发展现状及趋势[J]. 中国港口， 2016（4）：48-53.

（编辑 赵勉）