多属性决策的推荐系统赋权方法

叶 波， 李秉展, 谢 伟

(西南交通大学土木工程学院，四川成都 610000)

多属性决策是指在考虑多个属性情况下，选择最优备选方案或者进行方案排序的决策问题，通过计算和数学工具来支持决策对性能属性的评价。作为多属性决策中广泛使用的技术之一, TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution )是根据有限个评价对象与理想化目标的接近程度进行排序的方法[1]，是在现有的对象中进行相对优劣的评价。通过检测评价对象与最优解、最劣解的距离来进行排序，评价最好的对象应该是与最优目标的距离最近，而与最劣目标最远。距离的计算可采用Minkowski距离函数确定。文章研究采用TOPSIS作为基础方法，并将其扩展到推荐系统。

然而，在决策过程中，有许多应用，特别是在涉及政策，项目的不同重点或决策者的不同背景的情况下。决策者需要策略性地设置属性权重以获得他/她期望的备选方案的排名。 研究人员将MADM(Multi-Attribute Decision Making)中的根据决策者的偏好或者侧重点的调正称为策略权重调正问题。通常通过主观或者客观的方式确定更加准确的权重，而没有考虑策略权重调正问题的灵活性。总是一次性获得固定的权重。这意味着当决策者偏好或者侧重点发生变化时，需要重新运行方法。这样的方法，尤其对一些主观方法，缺少灵活性，且浪费人力物力资源，缺乏效率。

受人工智能技术广泛应用的启发，文章研究提出了一种多决策模型的权重调正推荐算子，能够根据决策者的反馈和协作能力提供连续学习和调整属性权重。通过赋予权重的学习能力，该算法能够适应和处理不同条件和不同需求的决策问题。此外，通过识别决策者偏好或侧重点变化，该算法能够及时生成新的权重，解决了传统决策模型缺乏灵活性的问题。

1 多属性决策模型的推荐者学习机制

1.1 框架结构

决策推荐系统框架如图1所示，主要是数据处理和排序推荐两个部分构成。由用户根据项目情况，输入方案的属性特征。系统运用TOPSIS和 Minkowski距离函数来整合数据，并计算出第一次排序结果。此结果作为推荐系统算子训练的初始数据。推荐算子部分根据用户要求为用户提供最准确的方案，通过不断获得对所推荐的排序结果的反馈进行学习，以满足用户的要求。更新的权重，作为用户当前的偏好权重。在下一次推荐时，将会依据用户的偏好权重，计算出最接近用户需求的方案。

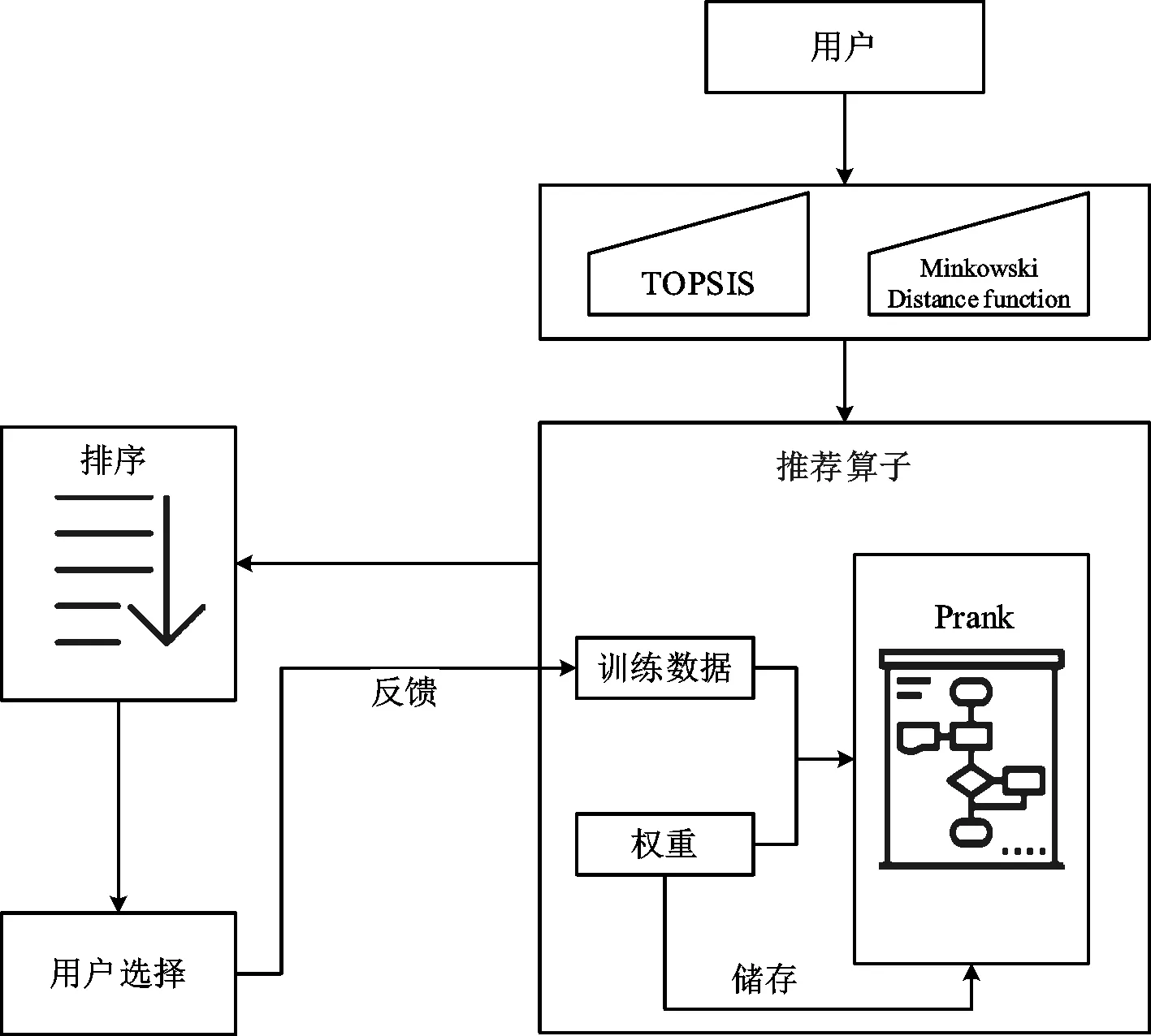
图1 框架结构

1.2 灰数多属性决策模型

基于灰数与Minkowski距离函数，多属性决策模型的主要步骤如下：

Step1：建立灰色决策矩阵Dk,Dk定义如下。

(1)

为了方便比较各个属性，首先进行决策矩阵归一化

(2)

最终构造归一化初始矩阵为

(3)

Step2：确定对于每个决策者的最优方案和最劣方案。

对于决策者k的最优解Ak+和最劣解Ak-的定义如下：

(3)

(4)

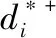
(5)

(6)

当p=2时，矩阵则是加权灰数的欧式距离函数：

(7)

(8)

Step4：计算各评价对象与最优方案的贴近程度。

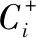
(9)

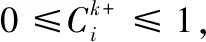
1.3 推荐系统算子

(10)

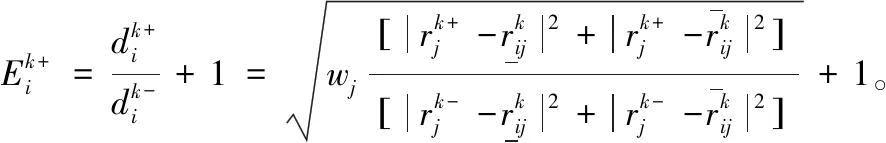
通常，属性的权重是通过主观设定，层次分析法或者专家组讨论得到。但并不是所有决策者都适用于这种方式得到的权重。因此，根据决策者的不同反馈改变权重是很有必要的。为了使系统更加智能化并增强TOPSIS的可靠性，我们提出了一种推荐器学习算子来调正不同情况和要求时的权重。该算子可以视作为TOPSIS的后处理器。

文章所用的推荐学习算子是基于Prank算法的单文档方法(pointwise approach of Learn to Rank)[2]。Prank算法是在感知器算法(perceptron algorithm)基础上开发的算法。该算子主要目的是从多属性决策模型获得前处理的数据，并计算推荐给用户的方案排序。同时，存储相应用户的权重。当用户下次选择方案的时候，推荐算子会基于用户的专属权重进行推荐。推荐算子调正权重的步骤如下：

Step 1：初始化。

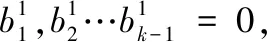
Step 2：排名判断。

对于r=1,…,y-1, 有xi·w≥br

对于r=y,…,k-1, 有xi·w≤br

以上表明预期的排名属于(by-1,by)的判断区间。如果所对应的yi匹配这个排序区间，则认为xi排序判断正确。

方便起见，判断条件可转化为：

对于r=1,…,y-1,xi·w≥br, 令yr=+1

对于r=y,…,k-1,xi·w≤br, 令yr=-1

新序列(y1,y2,…yk-1)=(+1,+1,…+1,-1,…,-1)的最大的索引值为r=y-1。

所以方案的正确排序判断则改为：

对于所有r,yr(xi·w-br)≥0

Step 3：判定修正。

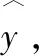
Step 4：循环。

迭代step 2和step 3，直到所有的排序都处于正确的区间，最后输出最终的w。

2 案例应用

2.1案例介绍

文章采用了台湾工程选择分包商的例子来证实所提出方法的可行性和实用性[3]。分包商的选择是建筑管理领域的一个重要问题。项目的成败通常会受到分包商工作质量的影响。通常，公司会邀请专家组组成决策小组，根据以下属性评估分包商：

(1)可靠性RA(Reliability ability)。分包商的可靠性是由其声誉，记录和财务状况来评估。

(2)进度控制能力SA(Schedule-control ability)。进度控制能力是由分包商的调动能力和效率来评估。

(3)管理能力MA(Management ability)。管理能力评估分包商的工作质量，安全性和环境管理。

(4)劳动力质量LQ(Labor quality)。劳动力质量评估分包商工人的技术和合作能力。

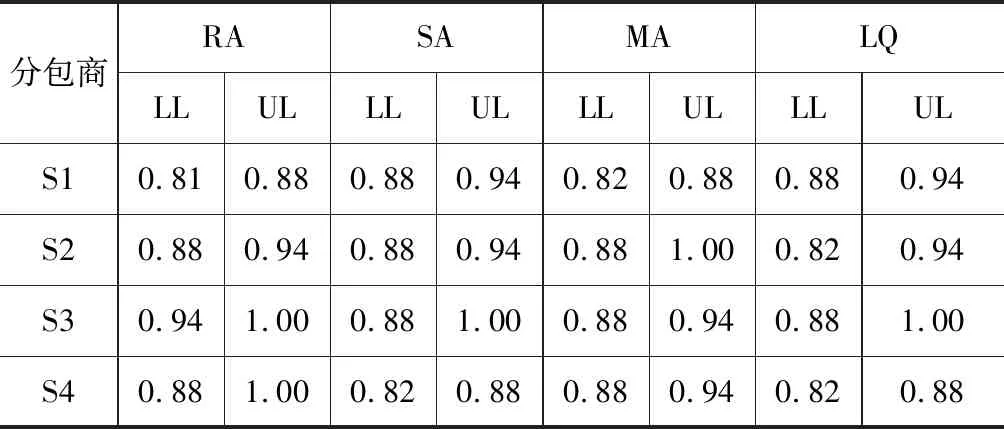
表1 分包商各属性数据

我们根据LIN表1提供数据选择了一段时期的评估结果并进行了归一化(包括每个灰数评估的下限LL和上限)，然后将各个属性的平均值乘以自身的权重，求和得到最终每个分包商的最终评分。初始化中每个权重设置为：w=[RA,SA,MA,LQ]=[0.25,0.25,0.25,0.25]。

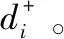
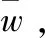
2.2 案例计算

根据表2，不难发现最初的默认排序是S3> S1> S4> S2。在这个等权重中的情况下， S3是最佳方案。每个分包商相应的排序编号，如S3 标记为1，表示S3 将在推荐列表中的第1名。

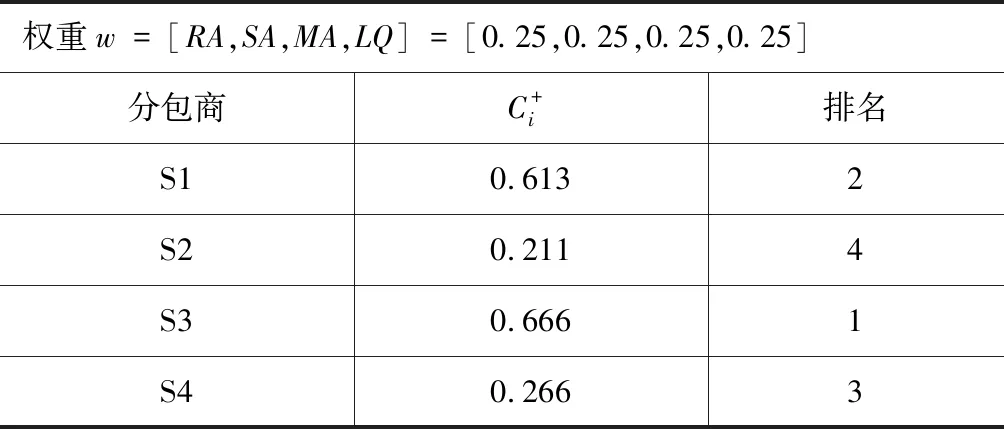
表2 等权计算结果

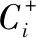
当该决策者下次进行分包商选择时，系统将会用所计算的权重，计算出符合她或他的偏好的分包商排序。

表3 推荐系统算子计算结果

计算的权重w=[RA,SA,MA,LQ]=0.2177,0.5088,0.2351,0.0384]

3 结 论

文章研究采用了Minkowski距离函数和TOPISIS技术，探究了权重和贴近程度的关系。同时，采用基于Prank的推荐学习算子来调整属性权重，提高了决策过程的可靠性，使模型更加灵活和智能，使决策者能够轻松快捷地找到有用的信息。采用了LIN论文案例和数据来解释该方法的应用,结果表明，权重的可变性克服了传统TOPSIS过度控制属性权重的缺点,多轮次的推荐学习算子对决策者实际应用帮助很大。

此外，文章内容是Lin方法的拓展。与原始方案相比，通过推荐学习算子代替了不同周期设置，受人工智能启发，推荐学习算子可以全面处理不同时期和不同用户需求。未来的研究将专注于更多的信息识别并整合到推荐系统中。