油气悬挂缸的力学特性数学模型构建方法

于子良，杨珏，马源，殷玉明，SUBHASH Rakheja

(1.北京科技大学 机械工程学院，北京，100083；2.中车工业研究院有限公司，北京，100070；3.浙江工业大学 机械工程学院，浙江 杭州，310023；4.康考迪亚大学 机械与工业工程系，蒙特利尔，H3G1M8)

油气悬挂是一种广泛应用于煤炭矿山运输车辆上的减振部件。油气悬挂利用气体的弹性与油液流经节流口的阻尼效应以及摩擦力构成其非线性特性。基于经典的气体状态方程和小孔节流公式可以建立基本的油气悬挂力学模型。经典的小孔节流公式根据小孔两侧压力差的变化计算油液流量的变化，本质上是一种差分方程，因此，经典小孔节流公式为基础的油气悬挂力学模型是一种差分模型。差分模型可以在特定激励下模拟悬挂的输出特性，但从整体上研究影响悬挂力学特性的规律比较困难。油气悬挂种类较多，本文研究对象为双腔单气室油气混合悬挂系统，该系统由活塞杆与缸筒组成，悬挂内部空间被分割为I 腔和II腔，I 腔中充满气体(一般为氮气)与油液，气体与油液之间无隔离层；II 腔中为油液。I 腔和II 腔由单向阀、阻尼孔以及活塞与活塞缸之间的缝隙连通，单向阀为无弹簧钢珠形式，在两侧压力差的作用下开通和闭合。影响油气悬挂阻尼特性的因素主要有激振信号的速度、阻尼孔、单向阀的直径等[1-2]。利用数学模型可研究一系列悬挂参数对悬挂特性的影响[3]。需要考虑的主要影响参数包括阻尼孔、单向阀截面积、II腔面积、油液密度和悬挂所受激励等。本文研究的悬挂缸结构较简单，但包含了油气悬挂缸主要的力学特性系统，如负责产生弹性的气室、负责产生阻尼力的阻尼孔和缝隙以及2个零件之间的摩擦部件。阻尼特性是此类悬挂缸的重要特性之一，机械部件特性与油液流体特性结合产生的阻尼特性更为复杂。CHO等[4]研究了一种臂式油气悬挂装置的阻尼特性，通过实验研究了阻尼孔的流量系数，但在连续性条件方程中使用了不可压缩的油液模型。程祥瑞等[5]基于薄壁小孔理论和范德瓦尔实际气体状态方程建立了单气室油气弹簧阻尼力特性模型，并推导了阻尼系数方程，用仿真方法研究了单气室油气弹簧阻尼特性以及激振频率、幅值、自身结构参数对阻尼系数速度特性的影响。王慧等[6]针对单气室油气弹簧系统，建立了接近实际工况的非线性负载和刚度特性数学模型，利用仿真方法进行油气弹簧的负载和刚度特性仿真分析，得出油气弹簧系统的氮气腔初始压力、氮气腔初始高度和活塞杆内径对刚度特性的影响规律。刘桓龙等[7-8]利用有限元分析软件对单气室油气悬挂缸工作流场进行仿真与分析，得出了油气悬架在不同工况下的阻尼特性曲线，为油气悬架的优化设计提供了参考依据。FARJOUD等[3]针对具有簧片系统的油气悬挂缸，讨论了簧片系统、阻尼孔开度以及油体积模量和油密度参数对阻尼特性的特性。封士彩等[9]研究了某起重机油气悬挂系统中阻尼孔、蓄能器及其管道尺寸对悬挂缸的阻尼特性的影响。MOUNIER-POULAT等[10]介绍了其通过设置阻尼孔的参数，完成了一种特殊油气悬挂缸的设计；FARJOUD等[11]讨论了簧片系统、阻尼孔开度以及油体积模量和油密度参数对阻尼特性的特性。CAO等[12]研究了连通式油气悬挂的动力学特性，引入了油液的可压缩性。在此，本文作者对单气室油气接触式悬挂系统的输出力学特性进行研究，分别建立气体部分状态模型、油液流经缝隙及小孔的节流方程模型以及摩擦力模型，从而建立完整的油气悬挂系统力学输出模型。在实验数据基础上分析油气悬挂系统的内能变化特点，研究油气悬挂结构参数与内能变化的关系，阐述其动力学特性。

1 工作过程描述及实验设计

双腔单气室油气混合悬挂系统结构如图1所示。

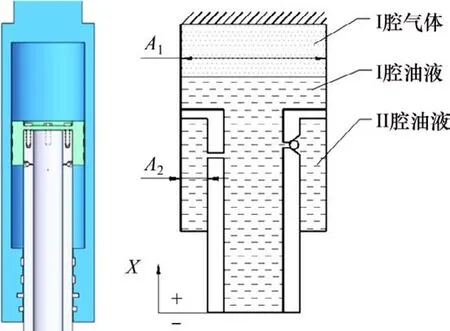
图1 双腔单气室油气悬挂物理模型Fig.1 Schematic of hydropneumatic suspension with dual chamber and single chamber

选取悬挂上换向点为工作循环起点，工作过程如下：活塞杆由悬挂上换向点向下运动，悬挂进入拉伸行程，I 腔容积增大，II 腔容积减小，II 腔油液由阻尼孔、活塞缸与活塞之间的缝隙流向I腔，单向阀在II 腔油液的高压作用下关闭。在该过程中，I 腔气体容积增加，气体和油液的压强降低，II腔油液压强增大。随压强降低I腔油液释放部分气体。

活塞杆至悬挂下换向点后开始向上运动，悬挂进入压缩行程，I腔气体容积减小，II腔气体容积增大，I 腔油液由阻尼孔、单向阀以及活塞缸与活塞之间的缝隙流向II腔。在该过程中，I腔液面上升，I腔气体被压缩的同时，部分气体溶解入油液中。实验测试装置如图2所示。悬架上端固定在横梁上，激励由活塞底端的振动器提供，力传感器安装在横梁与活塞缸之间。油压传感器1安装在活塞底端用于测量I腔油压，也就是气压。油压传感器2用于测量II腔油压。激振器施加给悬挂缸的激励是三角函数关系曲线。

图2 测试装置Fig.2 Test rig

2 系统各部分方程

2.1 气体方程

由于气体和油液是直接接触，气体在油液中存在溶解和析出的过程。在一定条件下，油液对气体的溶解存在饱和值[4]。随着保压时间增加或者外界激励时间增加，油液-气体系统中油液逐渐趋于饱和，在悬挂缸的压缩和伸张过程中溶解现象不再显著。在不同激励下，正弦激励周期内I腔压强的仿真结果和实验结果如图3所示。

从图3可以看出：I 腔压强的仿真结果与实验数据差距不大，因此可以认为在持续激励条件下，不考虑气体溶解和析出过程的模型能够近似反映气体状态的变化。

2.2 小孔流量和缝隙流量方程

小孔流量方程表达式[8,16]如下：

图3 不同激励下I腔压强的仿真结果与实验数据对比Fig.3 Comparison of gas pressure between simulation and test results of chamber I under different excitations

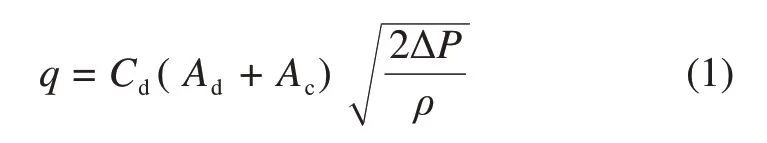
其中：q为节流口的流量；Cd为流量系数；Ad为阻尼孔的截面积；Ac为单向阀的截面积，在伸张行程中，单向阀关闭，此项为0；∆P为节流口两侧的压差；ρ为油液的密度。

缝隙流量方程表达式为

式中：D为外缸内径；d为活塞外径；μ为黏度系数，也称液体黏性的内摩擦因数；L为活塞与活塞缸之间缝隙长度。

2.3 基于差分模型的悬挂缸输出力计算模型

假设：

1)I腔油液和气体压力处处相等；

2)I腔气体的变化过程为理想气体变化过程；

罗恬拿着信纸，指尖不住地颤抖。她不知道自己费尽周折，担惊受怕换来的竟是这样的结局。可她分明看见杜朗站在楼梯下的阴影里，对她轻轻地挥手……

3)忽略气体溶解和析出对气体压强和油液压强的影响；

4)只考虑II 腔油液的可压缩性；I 腔中由于油液的可压缩性产生的体积变形与I腔气体变形量相比太小，I腔中油液的可压缩性忽略不计。

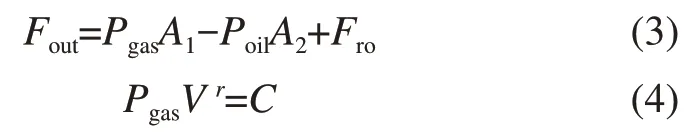
式中：Fout为悬挂输出力；Pgas为气体压强；Poil为油液压强；Fro为内缸外缸之间的摩擦力；r为气体多变指数；C为常数。

考虑到油液的可压缩性，油液体积模量为

式中：K为油液体积模量；V为油液体积；dP为油液压强变化量；dV为油液体积变化量。

II 腔油液的压强计算方法可以表示为密度的变化：

2.4 II腔油液压强计算模型

油气悬挂缸中I 腔的压力变化由气体状态确定，压力是油缸伸缩量位移的函数；II腔油压的变化由阻尼空、单向阀以及活塞和缸桶壁间的缝隙节流效果决定，是油缸伸缩速度的函数，当油缸伸缩速度很低时，I 腔和II 腔的油压保持接近。考虑油液弹性时，以式(1)～(6)为基础建立II 腔油压计算差分模型(模型1)，如图4所示。

若不考虑II腔油液的可压缩性，则可以根据II腔容积的变化确定两腔间的油液流量，再利用小孔流量式(1)和(2)用来计算压差，从而跟根据I腔压力得到II腔压力，其计算模型(模型2)如图5所示。

2种计算模型中，式(1)和(2)的运用方式不同，一种是利用压差计算流量，另一种是利用流量计算压差。在较低速激励条件下，2种计算模型所得结果差别不大，均与实验结果较好地吻合。随着激励频率的增加，考虑油液弹性的模型仍具有较高的精度，但忽略油液弹性的模型所得结果与实验结果差距较大。图6所示为4 Hz 激励频率下2 种模型计算方法得到的II腔油压对比。

图4 基于油液弹性的II腔油压计算模型(模型1)Fig.4 Simulation model(Model 1)of oil pressure in chamber II based on oil elasticity

图5 忽略油液弹性、基于容积变化的II腔油压计算模型(模型2)Fig.5 Simulation model(Model 2)of oil pressure in chamber II ignoring elasticity

图6 4 Hz激励下不同模型计算得到的II腔油压对比Fig.6 Comparison of oil pressure in chamber II calculated by different models under 4 Hz

2.5 摩擦力模型

很多研究者研究了缸类系统摩擦力模型的建立的问题，如Karnopp和Lugre 模型在很多场合下已经被证明是有效的[13-18]。关于摩擦力模型参数识别的方面，一般采用最小二乘法、遗传算法等方法。参数识别的关键在于保证足够的精度和计算效率。MARTON等[19]采用根据速度、油压信息进行的线性参数识别方法，其计算效率较高，并且准确度也能满足要求。

根据本文实验系统原理及测量数据，摩擦力可用下式求得：

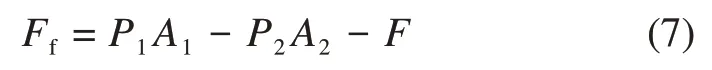
图7所示为不同激励条件下，摩擦力与活塞杆运动速度和位移之间的关系。由图7可以看出：模型具有较显著的Stribeck效应，即摩擦力随着相对运动速度的增大减小。Lugre 模型是一种考虑了Stribeck 效应的摩擦力模型[18]，方程如下：

其中：Fc为库仑摩擦力；Fs为最大静摩擦力；v为两表面间的相对速度；vs为Stribeck 速度；σ2为黏性摩擦因数。

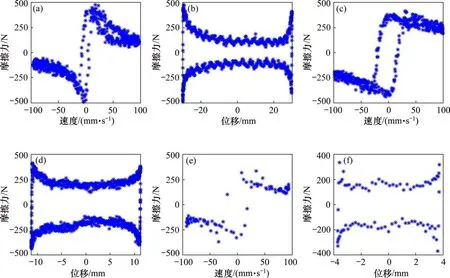
图7 不同激励条件下摩擦力与速度、位移的关系Fig.7 Friction vs.velocity and displacemen under different excitation conditions

由图7可见：摩擦力并未随速度(绝对值)的增加而增大，σ2的影响较小。针对每组实验结果可以进行摩擦力模型参数的识别。采用遗传算法，分别对Fc，Fs，vs和σ2进行识别。每组数据识别所得参数都有所差异，但其中黏性摩擦因数均接近0，后续模型计算中将此项忽略。

摩擦力仿真模型输出结果与实验结果对比如图8所示。从图8可以看出：摩擦力仿真模型基本能够反映摩擦力的变化特征。需要指出的是，对于已确定结构参数的悬挂缸，在不同的载荷及初始条件下，通过参数识别所得到的结果并不完全一致，即不能得到一个统一的Lugre模型。

图8 摩擦力模型仿真结果与实验结果对比Fig.8 Comparison of friction force between model andtest results

2.6 输出力方程

根据上述气体、油液压力模型和摩擦力模型，可以得到此类油气悬挂缸的输出力模型。悬挂缸输出力方程如下：

其中：A1为活塞缸截面积。

不同激励条件下悬挂输出力仿真模型输出结果与实验结果对比如图9所示。由图9可知：仿真模型输出结果与实验结果基本吻合，能够反映油气悬挂在拉伸、压缩过程中基本的力学特征。在激励速度较低的情况下，拉伸与压缩过程输出力差异不太大；随着激励速度增大，拉伸过程的阻尼力显著增大，这是由于油液流经阻尼孔或者缝隙过程中产生的压差，这也是油气悬挂非线性特性的主要构成部分。由于摩擦力换向过程产生的非线性特性，造成了悬挂缸输出力也存在较严重的非线性特性。

图9 不同激励条件下悬挂输出力仿真模型输出结果与实验结果对比Fig.9 Comparison of output-force between model and test results under different excitation conditions

3 结论

1)针对一种典型的油气悬挂系统，分析其中气体、节流阻尼和摩擦力的数学模型建立方法，并由这3个子系统的数学模型确定整个悬挂的输出力模型。

2)气体在油液中的溶解与析出不会对整个悬挂的输出力特征有显著的影响，在一定条件下可以忽略溶解过程。

3)由小孔节流、缝隙节流构建的悬挂阻尼力模型中，油液的弹性不可忽略，这是影响油液压力计算的重要特性；此类悬挂的摩擦力具有典型的Stribeck效应，以此为依据进行参数识别构建的摩擦力模型能够较好地还原悬挂输出力模型，但是由于在不同激励条件下，摩擦力模型中参数的识别结果并不一致，这也使得难以建立一个统一准确的悬挂缸输出力模型。

4)若要建立统一完整的悬挂力学特性模型，则还需要考虑其他方法。