基于系统效能的可靠性维修性指标确定方法

李京峰，项华春，蔡忠义，王泽洲

（空军工程大学装备管理与安全工程学院，西安 710051）

0 引言

关于可靠性、维修性理论及其技术的研究与应用在发达国家一直得到了高度重视，并且日趋成熟，目前已在机械、电子、航空等领域发挥了很大效益。我国从20世纪60年代开始也陆续进入了可靠性、维修性的研究当中。空军通过开展航空装备可靠性、维修性工作，使我国现役航空装备的可靠性、维修性水平得到了较大提高。提高航空装备的可靠性，将延长航空装备的无故障工作时间，减少故障发生的次数，降低维修费用，使航空装备持续工作及完成任务的能力增强；提高航空装备的维修性，将减少航空装备故障后的维修时间，提高维修效率，进而增强航空装备再次投入战斗的能力。

为了使航空装备可靠性、维修性研究工作更加符合作战需求，本文分析了效能及系统效能的定义，结合系统效能评估模型E=ADC提出了基于系统效能的可靠性、维修性指标定量要求，并用图形体现。同时，定量分析了使用可用度、可信度及系统效能增长对可靠性、维修性的影响。

1 系统效能概念分析

1.1 效能定义

效能是一个系统满足一组特定任务要求程度的度量；或者说是系统在规定条件下达到规定使用目标的能力的度量［1］。

1.2 系统效能定义

对于武器装备来说，其效能通常可以分为单项（指标）效能、系统效能和作战效能。其中，系统效能是指系统在规定的条件下和规定的时间内，满足一组特定任务要求的程度。它与可用性、任务成功性和固有能力有关［2］。

可用性是指产品在任一时刻需要和开始执行任务时，处于可工作或可使用状态的程度［2］。

任务成功性是指装备在任务开始时处于可用状态的情况下，在规定的任务剖面中的任一（随机）时刻，能够使用且能完成规定功能的能力。它取决于任务可靠性和任务维修性。原称可信性［2］。

固有能力是指装备在执行任务期间所给定的条件下，达到任务目的的能力。如杀伤力、最大速度、精度、射程等［2］。

1.3 系统效能评估方法

目前，对于武器装备系统效能评估分析的方法主要有：层次分析法、模糊综合评判法、灰色评估法、指数法、模拟仿真法、聚类分析法、ADC法和SEA 法等［3］。

其中，ADC法是20世纪60年代中期美国工业界武器效能咨询委员会（WSEIAC）为空军建立的评价武器系统效能的模型和方法，表示形式为：

式中，E为系统效能；A为可用度；D为可信度；C为固有能力。

ADC法公式透明性好，便于计算与理解，比较适用于不考虑对抗条件下的武器系统效能评估和简化情况下的宏观系统效能评估［4］，因而在学界得到了广泛的应用。基于以上分析，结合本文分析的对象特点，认为ADC法的可操作性比较大，故选取ADC法的计算模型作为以下分析的依据。

1.4 ADC模型简介

1.4.1 可用度A

可用度是可用性的概率度量。它是任务开始时装备处于各种状态概率的矩阵，即表示任一随机时刻任务开始时装备处于i状态的概率。在实践当中，根据不同的使用要求，可用度可以有不同的度量方式，通常包括固有可用度Ai、可达可用度Aa、使用可用度Ao3种度量方式。

1）固有可用度

式中，TBF为平均故障间隔时间（MTBF）；MCT为平均修复性维修时间（MTTR）。

该可用度是仅与工作时间和修复性维修时间有关的一种可用性参数。它没有考虑预防性维修和行政管理及保障延误对可用性的影响，而仅取决于产品的固有可靠性与维修性。它易于评估、测量，常在设计初期或签订合同时采用。

2）可达可用度

式中，TBM为平均维修间隔时间（MTBM）；MCT为平均修复性维修时间（MTTR）；MPT为平均预防性维修时间（MTPM）。

该可用度不仅与固有可靠性和维修性有关，还与预防性维修有关，仅仅没有考虑行政管理及保障延误的影响，是装备所能够达到的最高可用度，常在研制早期使用。

3）使用可用度

式中，TBF为平均故障间隔时间（MTBF）；MCT为平均修复性维修时间（MTTR）；TMD（TMD=TMLD+TMAD）为平均延误时间；TMLD为平均保障延误时间；TMAD为平均管理延误时间。

该可用度是与能工作时间和不能工作时间有关的一种可用性参数，它综合考虑了上述两种可用度没有考虑到的因素，反映了航空装备在实际使用条件下的可用程度，因此，本文选取了使用可用度模型作为分析模型。

1.4.2 可信度D

可信度是可信性（任务成功性）的概率度量。它是某一时间间隔内条件概率的矩阵，即

dij表示任务开始时装备处于i状态，经过预期任务时间装备处于j状态的概率［5-8］。

根据定义，可信度是任务可靠度与任务维修度的函数，但在航空装备执行任务期间一般是无法维修的，即任务维修度为零。此时，可信度就是任务可靠度，即

式中，t为本次任务执行时间；TBF为平均故障间隔时间（MTBF）。

1.4.3 固有能力C

固有能力是装备在执行任务期间所给定的条件下，达成任务目标的概率矩阵，即ci表示装备处于i状态时达成任务目标的概率。

2 基于使用可用度的可靠性维修性指标定量要求

2.1 使用可用度与可靠性、维修性指标的关系模型

由式（4）可得

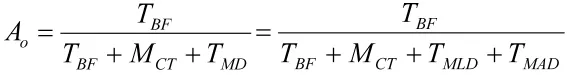
因此，

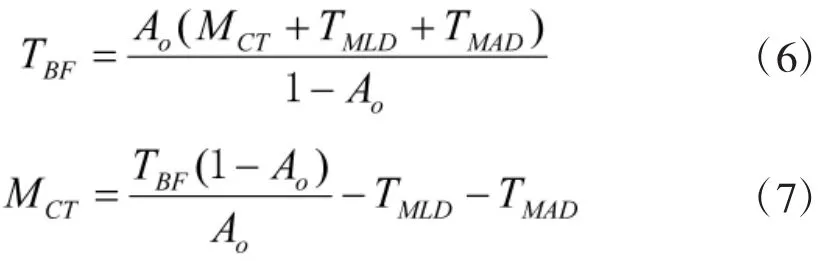
2.2 提高使用可用度对可靠性指标要求的影响

1）差值分析

在式（6）中，设 MCT不变，当 Ao变化 △Ao时，TBF由初始量TBF1变为TBF2，变化量为△TBF，即

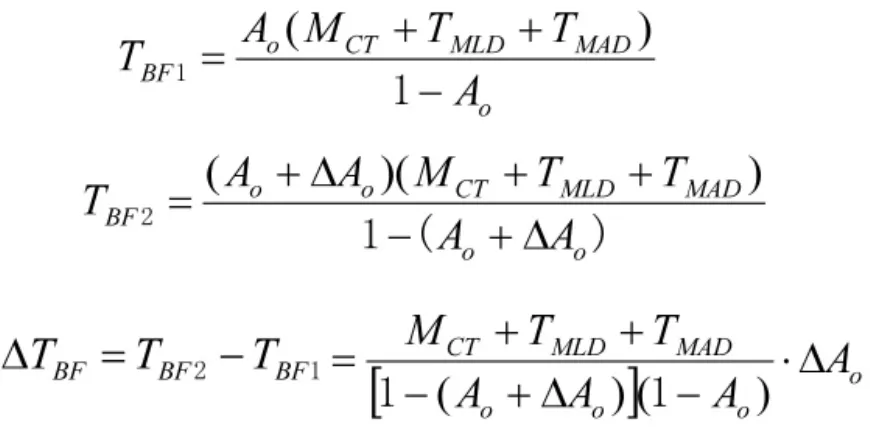
当使用可用度增长时，△Ao>0，则△TBF>0，所以，TBF随Ao增长而增长。

2）微分分析

在式（6）中，设 MCT不变，当 Ao变化 △Ao时，TBF变化 △TBF，即

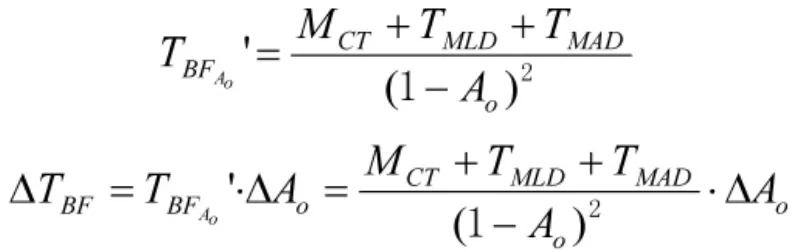
当使用可用度增长时，△Ao>0，则△TBF>0，所以，TBF随Ao增长而增长。在微分分析的基础上，经进一步分析，可以得到表1。

表1 以MCT=30 h为例（结果取整）

可以发现Ao在取0.6之后TBF的变化速度越来越快，极限值为无穷大。也就是说当Ao取到一定值时，要想继续提高使用可用度，可靠性就要得到更大的提高，也就意味着成本会显著增加。

利用Matlab图形分析工具，对使用可用度与可靠性之间的关系进行分析。假设某型飞机的TMLD与TMAD之和是500 h。由式（6），令MCT从上至下依次为30 h，25 h，20 h，15 h，10 h，可得曲线如图 1 所示。

图1 使用可用度与可靠性指标的关系曲线

从图1中可以看出，可靠性指标TBF随使用可用度Ao增大而增大。这与差值分析的结果相互吻合，其变化趋势也符合微分分析表格中的数据。

2.3 提高使用可用度对维修性指标要求的影响

1）差值分析

在式（7）中，设 TBF不变，当 Ao变化 △Ao时，MCT由初始量MCT1变为MCT2，变化量为△MCT，即

当使用可用度增长时，△Ao>0，则△MCT<0，所以MCT随Ao增长而下降，即维修性随使用可用度增长而增长。

2）微分分析

在式（7）中，设 TBF不变，当 Ao变化 △Ao时，MCT变化 △MCT，即

当使用可用度增长时，△Ao>0，则△MCT<0，所以，MCT随Ao增长而下降，即维修性随使用可用度增长而增长。在微分分析的基础上，经进一步分析，可以得到表2：

表2 以TBF=3 000 h为例（结果取整）

可以发现Ao在取0.4之前MCT的变化速度非常快，在Ao=0时MCT=∞，Ao=1时MCT=-500。也就是说当Ao取到一定值时，要想继续提高使用可用度，维修性就要得到更大的提高，也就意味着成本会显著增加。

利用Matlab图形分析工具，对使用可用度与维修性之间的关系进行分析。假设某型飞机的TMLD与TMAD之和是500 h。由式（7），令 TBF从上至下依次为 3 000 h，2 500 h，2 000 h，1 500 h，1 000 h，可得曲线如图2所示。

图2 使用可用度与维修性指标的关系曲线

从图2中可以看出，维修性指标MCT随使用可用度Ao增大而减小。这与差值分析的结果相互吻合，其变化趋势也符合微分分析表格中的数据。

在分别分析了使用可用度与可靠性、维修性指标之间的关系后，接下来进行使用可用度与可靠性、维修性指标关系的综合分析。由式（6），取Ao（0.75~0.85），得图 3。

从图3中可以看出，当使用可用度Ao增大时，TBF增大，MCT减小。

图3 使用可用度与可靠性、维修性指标的关系曲线

3 基于可信度的可靠性指标定量要求

3.1 可信度与可靠性指标的关系模型

根据式（5）的可信度模型

得到

3.2 提高可信度对可靠性指标要求的影响

1）差值分析

在式（8）中，当D变化△D时，TBF由初始量TBF1变为 TBF2，变化量为 △TBF，即

当可信度增长时，△D>0，则△TBF>0，所以可靠性随可信度D增长而增长。

2）微分分析

在式（8）中，当 D 变化 △D 时，TBF变化△TBF，即

当可信度增长时，△D>0，则△TBF>0，所以可靠性随可信度D增长而增长。在微分分析的基础上，经进一步分析，可以得到下页表3所示。

可以发现D在取0.6之后TBF的变化速度越来越快，极限值为无穷大。

利用Matlab图形分析工具，对可信度与可靠性之间的关系进行分析。当任务执行时间t从上至下依次为 5 h，4 h，3 h，2 h，1 h 时，根据式（8），可得曲线如图4所示。

表3 以t=1 h为例（结果保留两位小数）

图4 可信度与可靠性指标的关系曲线

从图4中可以看出，可靠性指标TBF随可信度D增大而增大，尤其是在D取0.95之后，它的增大对TBF的影响更加明显。这与差值分析的结果相互吻合，其变化趋势也符合微分分析表格中的数据。

4 基于系统效能的可靠性维修性指标定量要求

4.1 系统效能与可靠性、维修性指标的关系模型

对于航空装备而言，在执行任务期间发生的故障通常难以修复（如战斗机），那么可以按如下方法建立E的表达式。

按照上述假设，航空装备在任务开始时只有两种状态，即正常和故障，因此，

1）可用度矩阵A为

式中

2）可信度矩阵D为

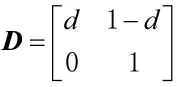
式中

3）固有能力矩阵C为

由公式E=ADC可得

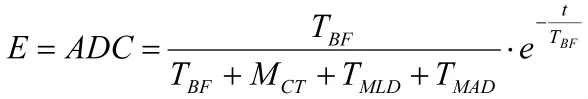
因此，

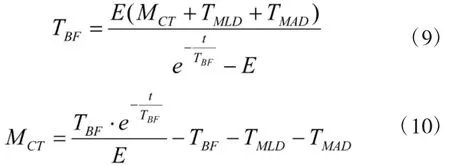
4.2 提高系统效能对可靠性指标要求的影响

1）差值分析

在式（9）中，设 MCT不变，当 E变化△E时，TBF由初始量TBF1变为TBF2，变化量为△TBF，即

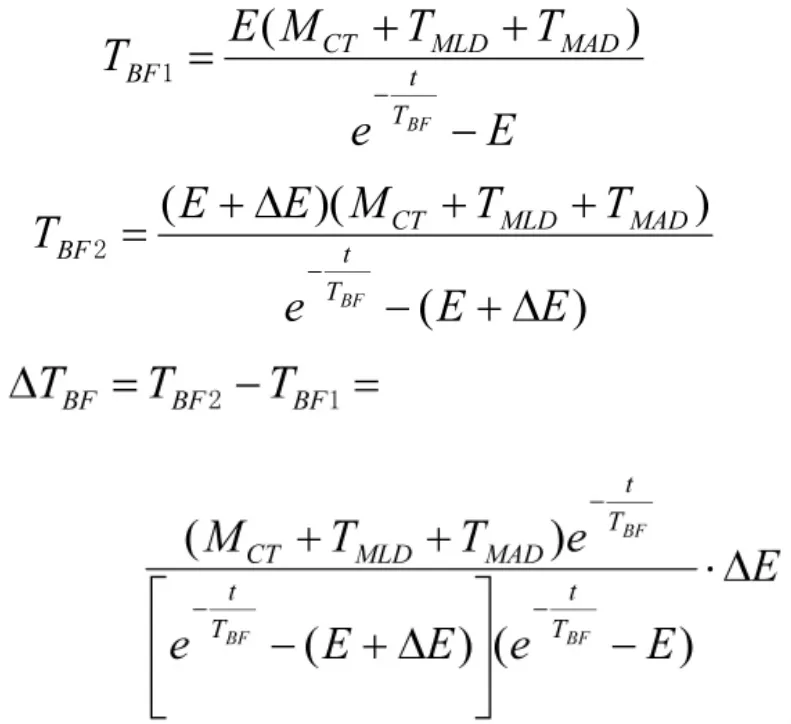
当系统效能增长时，△E>0，则 △TBF>0，所以，TBF随E增长而增长。

2）微分分析

在式（9）中，设 MCT不变，当 E变化△E时，TBF变化△TBF，运用隐函数求导可得

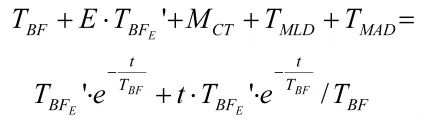
整理得

当系统效能增长时，△E>0，则 △TBF>0，所以，TBF随E增长而增长。在微分分析的基础上，经进一步分析，可以得到下页表4。

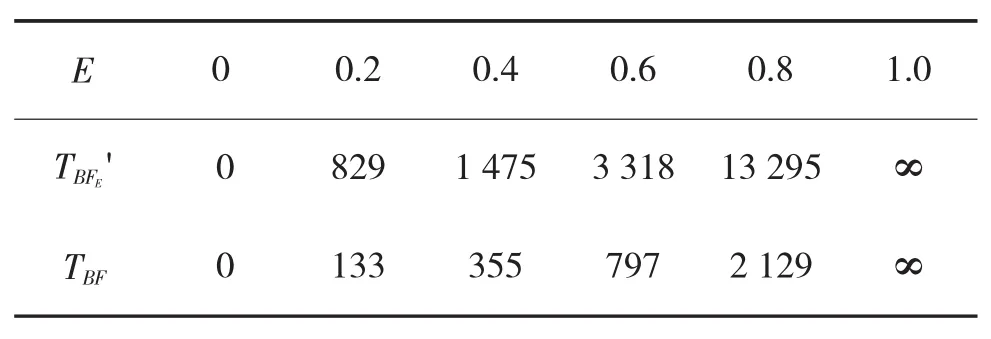
表4 以MCT=30 h，t=1 h为例（结果取整）

可以发现E在取0.6之后TBF的变化速度越来越快，极限值为无穷大。也就是说要想继续提高系统效能，可靠性就要得到更大的提高，也就意味着成本会显著增加。

根据上述假设，某型飞机的TMLD与TMAD之和是500 h，任务执行时间是 1 h。由式（9），令 MCT从上至下依次为 30 h、25 h、20 h、15 h、10 h，可得曲线如图5所示。

图5 系统效能与可靠性指标的关系曲线

从图5中可以看出，可靠性指标TBF随系统效能E增大而增大。这与差值分析的结果相互吻合，其变化趋势也符合微分分析表格中的数据。

4.3 提高系统效能对维修性指标要求的影响

1）差值分析

在式（10）中，设TBF不变，当E变化△E时，MCT由初始量MCT1变为MCT2，变化量为△MCT，即

当系统效能增长时，△E>0，则△MCT<0，所以，MCT，随E增长而下降，即维修性随系统效能增长而增长。

2）微分分析

在式（10）中，设TBF不变，当E变化△E时，MCT变化 △MCT，即

当系统效能增长时，△E>0，则△MCT<0，所以，MCT随E增长而下降，即维修性随系统效能增长而增长。在微分分析的基础上，经进一步分析，可以得到表5。

表5 以TBF=3 000 h，t=1 h为例（结果取整）

可以发现E在取0.4之前MCT的变化速度非常快，在E=0时MCT=∞，E=1时MCT=-500。也就是说如果继续提高系统效能，维修性就要得到更大的提高，也就意味着成本会显著增加。

根据上述假设，某型飞机的TMLD与TMAD之和是500 h，任务执行时间是 1 h。由式（10），令 TBF从上至下依次为 3 000 h、2 500 h、2 000 h、1 500 h、1 000 h，可得曲线如图6所示。

图6 系统效能与维修性指标的关系曲线

从图6中可以看出，维修性指标MCT随系统效能E增大而减小。这与差值分析的结果相互吻合，其变化趋势也符合微分分析表格中的数据。

在分别分析了系统效能与可靠性、维修性指标之间的关系后，接下来进行系统效能与可靠性、维修性指标关系的综合分析。由式（9），取E（0.5~1），可得如下页图7所示。

从图7中可以看出，系统效能E增大时，TBF增大，MCT减小。根据系统效能E的要求，便可以确定可靠性指标TBF和维修性指标MCT的值，从而达到预期目标。

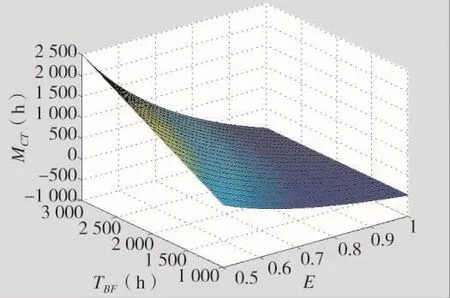
图7 系统效能与可靠性、维修性指标的关系曲线

5 结论

本文在界定效能和系统效能概念的前提下，结合使用可用度增长、可信度增长、系统效能增长对可靠性、维修性指标影响的定量分析，最终明确了基于系统效能的可靠性、维修性指标定量要求。该研究成果为航空装备更加贴近实战背景提高可靠性、维修性指标提供了量化分析工具，为更有目的性地开展航空装备可靠性、维修性工作提供了理论支撑，并且具有一定的应用前景。比如：可以通过划分不同机种的系统和机载设备，确定出各机种的重点系统和机载设备，根据本文的研究成果进一步将基于系统效能的可靠性、维修性指标分配到重点系统和机载设备，从而建立起系统效能与重点系统和机载设备之间的定量计算模型，提高研究的科学性、客观性、有效性和可操作性。并且可对航空装备可靠性、维修性工作项目的完成情况进行评价，保证工作的完成质量。