Defense Strategies Against Network Attacks in Cyber-Physical Systems with Analysis Cost Constraint Based on Honeypot Game Model

Wen Tian, Xiaopeng Ji, , Weiwei Liu, Guangjie Liu, Rong Lin, , Jiangtao Zhai and Yuewei Dai

Abstract: Cyber-physical system (CPS) is an advanced system that integrats physical processes, computation and communication resources.The security of cyber-physical systems has become an active research area in recent years.In this paper, we focus on defensive strategies against network attacks in CPS.We introduce both low- and highinteraction honeypots into CPS as a security management tool deliberately designed to be probed, attacked and compromised.In addition, an analysis resource constraint is introduced for the purpose of optimizing defensive strategies against network attacks in CPS.We study the offensive and defensive interactions of CPS and model the offensive and defensive process as an incomplete information game with the assumption that the defender's analysis resource is unknown to the attacker.We prove the existence of several Bayesian-Nash equilibria in the low- and high-interaction honeypot game without analysis cost constraints and obtain the attacker's equilibrium strategy firstly.Then, we take the impact of analysis cost on the capture effect of honeypots into consideration and further optimize the defensive strategy by allocating analysis resource between low- and high-interaction honeypot with resource constraint.Finally, the proposed method is evaluated through numerical simulation and prove to be effective in obtaining the optimal defensive strategy.

Keywords: Honeypot, game theory, cyber-physical system, network attack, human analysis cost.

1 Introduction

Cyber-physical system (CPS) refers to a new generation of systems with integrated computing and physical capabilities that can interact with humans through many new modalities.These systems can be found in many key infrastructures such as smart grids, chemical plants, and transportation systems [Li, Zhang, Zheng et al.(2017); Celli, Pegoraro, Pilo et al.(2014); Liu, Luo, Liu et al.(2018)].In the past few decades, the development of control algorithms and technologies has greatly improved the adaptability and robustness of the system [Yağan, Qian, Zhang et al.(2012)].While the technologies can significantly improve the resilience of the integrated systems, the CPS security has become an important subject of research and development due to the growing number of cyber-attacks in recent years [Humayed, Lin, Li et al.(2017); Amin, Schwartz and Hussain (2013); Yang, Zhou, Yang et al.(2018)]

Security issues in the CPS can be grouped into four categories: confidentiality, integrity, availability, and authenticity [Von Solms and Van Niekerk (2013); Banerjee, Venkatasubramanian, Mukherjee et al.(2012)].Among the various threats in CPS, network attack is a typical attack mode, which seriously threatens the data and communication.Network attack refers to any event that can control or eliminate the normal execution of the network [Pasqualetti, Dorfler and Bullo (2013)], or invade the system through a system vulnerability.With the continuous development of network attack technology, new forms of security threats continue to emerge and evolve [Nappa, Johnson, Bilge et al.(2015)].However, defense technologies usually cannot keep up with the pace of change in security threats, which greatly worsens the security situation of CPS.As an active defense technology [Spitzner (2003)], honeypot technology is essentially a technique for defrauding attackers by arranging some hosts, network services, or information as bait, which induces attackers to attack them so that they can capture and analyze attack behavior [Cao, Liu and Xu (2004); Zhang, Zhou, Qin et al.(2003)].

Distinct from other security tools, most honeypots can only generate reports due to their low degree of automation.However, the participation of human is required to analyze and capture attacks for most honeypots.Therefore, human analysis costs became an important factor for the success of honeypot capture [Ghourabi, Abbes and Bouhoula (2013)].In addition, in real scenarios, honeypots can always be classified as high-interaction honeypots and low-interaction honeypots.High-interaction honeypots can completely imitate service like real servers [Alata, Nicomette, Kaaniche et al.(2006)] and low-interaction honeypots can only provide partial service [Mukkamala, Yendrapalli, Basnet et al.(2007)].To best of our knowledge, little existing work has been done that focus on the use of honeypots in attack-defense game with the consideration of human analysis cost constraint and honeypot classification, and is not adequate to deal with the actual attacks [Nawrocki, Wahlisch, Schmidt et al.(2016)].This motivates the present study.

In this paper, we study defensive strategies against network attacks in CPS with human analysis cost constraint.We analyze the offensive and defensive interactions and model the offensive and defensive process as an incomplete information game with the assumption that the defender’s analysis resource is unknown to the attacker.We prove the existence of several Bayesian-Nash equilibria in the low- and high-interaction honeypot game (LHHG) without analysis cost constraints, obtain the optimal deployment strategy and get the attacker’s equilibria strategy firstly.Then, we take the impact of human analysis cost on the capture effect of honeypots into consideration and further optimize the defensive strategy by allocating human analysis cost between low- and highinteraction honeypot with cost constraint.It is shown that the proposed model and approach can optimize defense performance with limited human analysis costs.The main contributions are summarized as follows.

(1) We introduce honeypots into the security of CPS.At the same time, we classified honeypots into high- and low-interaction honeypots in order to make the interaction process more accurate.

(2) We also introduce human analysis cost constraint in the honeypot to maximize the defense payoff since defender’s budget is usually insufficient in practice.

The rest of the paper is organized as follows.Section II provides a summary of related work from other researchers.Section III describes the proposed low- and high-interaction honeypot game model based on the game tree.In Section IV, the existence of Bayesian Nash equilibria with sufficient analysis cost is proved, and the defensive strategy with human analysis cost constraint is optimized.In Section V, extensive numerical simulation using MATLAB is carried out to evaluate the proposed method.Finally, a conclusion is given in Section VI.

2 Related works

In this section, we briefly summarize the latest technical literature on security issues in CPS, honeypot for network attack and the use of game theory for modeling offense and defense process.

2.1 Security issues in CPS

Security issues in CPS have been widely studied in the past few years.Current research focuses on different areas such as smart grids, high confidence medical devices and systems, robots, distributed robotics, and transportation.Some work mainly focuses on intrusion detection.For example, Faisal et al.[Faisal, Aung, Williams et al.(2015)] proposed an intrusion detection system (IDS) architecture that uses the AMI data flow in the smart grid to analyze the performance of existing data flow mining algorithms and IDS data sets.However, with more and more interactions between physical systems and cyber systems, physical systems have a greater impact on security vulnerabilities.In 2010, the attacker demonstrated a software tool called CarShark [Koscher, Czeskis, Roesner et al.(2010)] that can kill the car engine remotely, turn off the brake system so that the car cannot stop, and carry out attack by monitoring the communication between the electronic control units (ECUs) and inserting forged packets so that the instrument gives erroneous readings.Actually, there are more and more security vulnerabilities in CPS like electronic power grids, smart transportation systems, and medical systems, and so on.

In addition, we can list several possible threats related to the development of CPS as follows: 1) High complexity may cause some unknown vulnerabilities and make the network to be vulnerable.2) CPS contains different networks, so the interaction between the networks easily leads to new types of attacks and further leads to the collapse of the defense system.3) Multiple nodes in the network are potential threats because they are very vulnerable to attackers.

2.2 Honeypot for network attack

The concept of honeypot technology first appeared in the book “The Cuckoo’s Egg” published in 1989 [Stoll (1989)].This book describes how to use honeypot technology to discover and trace the story of a commercial espionage case.In particular, honeypots only analyze incoming traffic and generate reports compared to traditional defense tools.Then human analysis is very necessary to mark and capture the attackers, otherwise there is no defensive effect.Since 1998, honeypot technology has gradually attracted the attention of security researchers who have developed honeypot software tools specifically designed to deceive attackers.The most famous is DTK (deception toolkit) developed by the famous computer security expert Cohen [Cohen (1998)].Traditional network attacks and malicious code on the Internet mainly use the security vulnerabilities or configuration weaknesses in network services to pose a threat to the target information system and the network.Therefore, the earliest honeypot tool software is also designed for network service attacks.Provos [Provos (2004)] presented “honeyd”, which is a honeypot software package to monitor large-scale honeynet.Vetsch [Vetsch (2011)] focuses on Web application attacks such as remote file packages and local file packages to simulate the exploit process and generate response results.Meanwhile, the attack log and the malicious script file are recorded by triggering the attacker to further malicious requests.Some previous studies pointed out the idea that honeypots can be deployed in the CPS to attract, detect, and gather attack information [Wang, Du, Maharjan et al.(2017)].However, none of these studies considers the involvement of human analysis costs.In addition, the realization of the spoofing environment construction mechanism determines the degree of interaction that the honeypot can provide for the attacker.Hastings et al.[Hastings, Laverty and Morrow (2014)] set a low-interaction honeypot in the smart grid and recorded the attack data for 6 months.HoneyBow [Zhuge, Holz, Han et al.(2007)] used a high-interaction honeypot that has the advantage of capturing more malicious code and capturing unknown samples.

2.3 Game theory for modeling

Game theory has been widely used in offensive and defensive modeling of CPS.For defenders, the intrusion detection system of passive defense response equipment has become a necessary complement to the security of CPS due to the increasingly serious types of attacks in recent years [Hodo, Bellekens, Hamilton et al.(2016)].Wang et al.proposed a non-cooperative game framework to solve different aspects of intrusion detection [Wang, Ouyang, Krishnan et al.(2015)].They put forward an approach of dynamically adjusting host-based IDS (HIDS) monitored objects based on the expected attacks based on non-cooperative games.Mohi et al.[Mohi, Movaghar and Zadeh (2009)] and Zang et al.[Zang, Liu and Yu (2007)] used the Bayesian game method for intrusion detection in Ad hoc networks.Specifically, they developed a two-player game with nonzero and incomplete information to provide a framework for IDS to minimize its losses based on its own beliefs.The reason for choosing a Bayesian game is that the interaction between the attacker and the defendant is usually an incomplete information game in which the defender or attacker is not sure of the type of other players.

In terms of the budget of human analysis cost, the most current researchers assume the human analysis cost is sufficient.However, to the best of our knowledge, due to their low degree of automation most honeypot cannot capture network attack without participation of human in the offensive and defensive interacting processes.In terms of the incomplete information, the attacker must assume a sufficient defender’s budget for insurance, as they have no idea about the accurate amount of the defender’s budget.From the defender’s perspective, the human analysis cost is usually insufficient.Therefore, we should consider the human analysis constraint in the further study of defensive strategy, which is closer to the real facts.In terms of application scenarios, no matter the behavior analysis of industrial network or the virtual network, they in essence base on the strategies selections, so that the researches on the issue of strategy selection is more general.

3 Low- and high-interaction honeypot game model of CPS

In this section, we describe the CPS structure and its potential security issues.Then, we introduce the low- and high-interaction honeypot game modeling based on the game tree.

3.1 CPS structure

CPS is an advanced form of a large multi-component automation system.The structure of CPS consists of the cyber layer and physical layer.Cyber layer consists of control systems and communication networks.Physical layer consists of various physical plants.Typically, Sensors and actuators achieve interaction between the cyber layer and the physical layer.The sensors transfer the measured physical quantities to the control system through the communication network at first.Then, the control system makes computations and decisions, and issues control instructions to the actuators and drive the operation of physical plants after receiving the signals from the sensors.

With the deep coupling of the cyber layer and the physical layer, attacks on the physical process initiated through the cyber layer are increasing in recent years.Therefore, the security of the cyber layer is also essential to ensure the security of the CPS.In this paper, we introduce honeypots to protect against network attacks in the CPS.

We first provide a brief explanation for the architecture of the CPS and its components: A typical access diagram in the CPS is shown in Fig.1(a).Visitors represent the users accessing CPS, including legitimate users and attackers, and all users’ access CPS resources over the Internet.Firewall is a security protection system that allows or restricts the transmission of data in accordance with specific rules.Router is used to connect multiple logically separate network devices, such as servers that receive, process, store and transmit data from sensors.Meanwhile, in order to increase the security level of CPS, many honeypots coexist with servers.In this paper, we consider the case where honeypots are deployed in network terminals.

Then, we briefly introduce the interaction between the visitors and CPS.When the visitor is a legitimate user, the router assigns the visitor to the normal server to get the service.However, there exist many attackers in visitors who impersonate legitimate users.For these attackers, they first explore vulnerabilities in the CPS and are apt to launch offensive access by exploiting the vulnerabilities.So all network attacks into the CPS will be directly tricked into the honeypots because honeypots will actively expose many vulnerabilities.In this paper, we assume that an offensive access is tricked into a highinteraction honeypot or a low-interaction honeypot with equal probability.The access diagram from attacker's perspective is shown in Fig.1(b).

Figure 1: User access diagram

3.2 LHHG modeling based on the game tree

In this subsection, we first analyze the objects of the attacker and SP.For the attacker, the goal is to identify honeypots and maximize payoff.We assume that the attacker has two offensive access types: strong offensive access and weak offensive access in this paper.We believe that a strong offensive access has a better recognition effect on the honeypot, but it consumes more resources.In contrast, weak offensive access has a worse recognition effect on the honeypots, but it consumes fewer resources.For the SP, the goal is to capture the attacker and maximize the payoff or minimize the loss of CPS.The honeypots of SP are classified into two modes: low-interaction honeypots and highinteraction honeypots.High-interaction honeypots imitate the activities of a CPS like servers and capture extensive information.The attacker can access all commands and files on the system with access right, so this mode of honeypot has the greatest potential for collecting information but also consume the greatest defense resources to maintain.Unlike high-interaction honeypots, low-interaction honeypots simulate only the services frequently targeted by attackers and so are less risky and less complex to maintain.We define the LHHG as a tuple: G≜＜Z , W , FZ, FW, UZ,UW＞.Z ∈{ Z1, Z2} is the mode of SP,1Z indicates low-interaction honeypot and2Z indicates high-interaction honeypot.W ∈{W1, W2} is the type of offensive access, W1indicates weak offensive access and W2indicates strong offensive access.FZ∈{Ω1, Ω2} is a binary strategy used by SP of mode Z, where1Ω indicates that SP provides services and2Ω indicates that services are not provided.FW∈{ν1,ν2} is a binary strategy used by attackers of type W , where ν1indicates that the attackers launch the offensive access and2ν indicates the offensive access are not launched.( FW1, FW2, FZ1, FZ2) is a set of game strategies for attackers and service providers.ZU andWU represent the payoffs of SP and attackers, respectively.The detailed list of notations is provided in Tab.1.

Table 1: List of symbols in the paper

In summary, there are two modes of honeypots, and each honeypot has two different strategies (provides services or not).Similarly, there are two types of offensive access, each type has two different strategies (initiate or not initiate access).Hence, there are 16 cases as shown in Fig.2(a) and Fig.2(b).

If the low-interaction honeypot provides effective service and the weak offensive access escapes capture, the payoff for the SP is -ς1(ς1＞ 0, ς1indicates the reward of attackers attacking low-interaction honeypots successfully).The payoff for the attackers is ς1- γ1( γ1represents the cost of attackers’ weaker offensive access).However, if the weak offensive access does not escape capture, the payoff for the SP is β (β ＞ 0,β indicates the reward of CPS working normally).The payoff for the attackers is -γ1.Similarly, if the low-interaction honeypot provides services and the strong offensive access escapes capture, the payoff for the SP is -ς1.The payoff for the attackers is ς1- γ2( γ2＞ γ1, γ2represents the cost of strong offensive access).By contrast, when the strong offensive access does not escape capture, the payoff for the SP is β and the payoff for the attackers is2γ- .Furthermore, if the high-interaction honeypot provides effective service and the weak offensive access escapes capture, the payoff for the SP is-ς2(ς2＞ ς1, ς2indicates the reward of attacker attacking high-interaction honeypots).The payoff for the attackers is ς2- γ1.Moreover, if the high-interaction honeypot provides effective services and strong offensive access escapes capture, then the attacker’s payoff is ς2- γ2.The payoff for the SP is-ς2.

Table 2: The escape probability of offensive access

In the LHHG, the SP does not know the type of offensive access in advance, but it has a priori information about certain statistical metrics of access, such as the distribution of access types.According to Harsanyi transformation, we assume p (W1)= 1 -α,p (W2)= α where α is the probability of strong offensive access.Similar to SP, we also assume that attackers also know the probability distribution of the mode of SP, where p (Z1)= 1 -θ,p (Z2)= θand θ is the probability distribution of highinteraction honeypots.As we know, the players participating in the game understand each other's strategies, so we use Bayesian rules to get the player's posterior probability and use it to calculate the expected maximum payoff for all players.Obviously, all potential strategies (FZ1,FZ2) that the SP can provide are as follows: {(Ω1,Ω1),(Ω1,Ω2) ,(Ω2,Ω1), (Ω2,Ω2)} which indicates the strategies of both low-interaction honeypot and highinteraction honeypot, respectively.Analogously, all potential strategies (FW1,FW2)that the attackers can use are as follows: {(ν1,ν1) , (ν1,ν2) , (ν2,ν1) , (ν2,ν2)}, which indicates the strategies of both strong offensive access and weak offensive access, respectively.To best of our knowledge, the SP cannot guarantee full capture of offensive access, even if it is for a specific offensive access behavior.Therefore, a unit honeypot can only capture offensive access successfully with a probability, and the escape probabilities of offensive access are shown in Tab.2.

For the SP, the capture probabilities of low- or high-interaction honeypot varies with the number of low- and high-interaction honeypots respectively.The expected escape probabilities of strong offensive access and weak offensive access to the number of low- or high- interaction honeypots with human analysis costs participation n is measured by functionbecause when there is only one honeypot, the escape probability of the offensive access for the SP is the escape probability of the offensive access for the honeypot; (b) aiis the minimum escape probability that an offensive access faces the CPS because no SP can fully capture the offensive access; and (c) Ψiis strictly decreasing and convex, because the escape probability from similar offensive access to similar honeypot decreases yet flattens out with the increase of the number of the similar honeypots [Levine, LaBella, Owen et al.(2003)].This set of conditions on the function Ψiis referred to as the generic conditions, and those functions that satisfy the generic conditions are referred to as the generic functions.

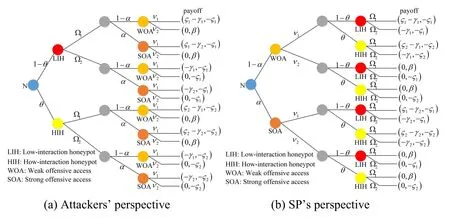
Figure 2: The game tree from perspective of attackers and SP

In order to express the payoffs of SP and attackers in different situations clearly, the game tree is a common way to show it.Fig.2(a) and Fig.2(b) show the game trees from the attackers’ perspective and SP's perspective when the offensive access is successful, respectively.The first term in each bracket in the Fig.2(a) and Fig.2(b) is the payoff of the attackers and the second term is the payoff of the SP.

4 The optimal defensive strategy under human analysis cost constraint

In this section, we analyze the offensive and defensive interactions and model the offensive and defensive process through an incomplete information game.In particular, we assume that the attacker thinks the human analysis cost of the defender is sufficient for insurance.Based on this assumption we prove the existence of several Bayesian-Nash equilibria in the LHHG with sufficient human analysis cost and obtain the attacker’s equilibrium strategy and the optimal deployment strategy of high- and low-interaction honeypots firstly.We then consider the impact of insufficient human analysis cost on the honeypot capture effect and further optimize the defensive strategy to maximize the payoff for SP by allocating insufficient analysis cost between low- and high- interaction honeypots.

4.1 The optimal defensive strategy with sufficient human analysis cost

Distinct from other security tools, most honeypots can only generate reports due to their low degree of automation, so the participation of human is very necessary to analyze and capture offensive access.Therefore, the attacker usually thinks that the human analysis cost of the defender is sufficient in the case of asymmetric information for the sake of insurance.

For the low-interaction honeypot that provides service, its payoff UZ1( Ω1)is denoted as

The payoff of the low-interaction honeypot for the strategy2Ω can be computed as

For the high-interaction honeypot that provides service, the payoff for the strategy1Ω and Ω2are expressed below respectively.

From Eqs.(1)-(4), no matter how the values of ς1,ς2, Ψ1, Ψ2, Ψ3,Ψ4andα changed in the feasible domain, the relationsUZ1( Ω1)＞UZ1( Ω2), UZ2( Ω1)＞UZ2( Ω2)are always hold true.Therefore, it is obvious that SP have a strict dominant strategy( Ω1, Ω1).Similar to SP, the payoff of the weak offensive access using strategy ν1is as follows:

The payoff of weak offensive access using strategy2ν can be expressed by

The payoff of the strong offensive access using strategy1ν and2ν can be expressed by

From Eqs.(5)-(8), the payoffs are dependent on the value of parameters and the attacker does not have a strict dominant strategy.

Theorem 1.A BNE strategy (ν1,ν1, Ω1, Ω1)exists in the LHHG model if

Proof of Theorem 1.In order to make (ν1,ν1, Ω1, Ω1)a BNE strategy, for attackers, the payoff of the offensive access is greater than the payoff from not launch offensive access, which meansUW1( v1)＞UW1( v2)andUW2( v1)＞UW2( v2).Then, we have

From the perspective of the attackers-side, when the service provider is a low-interaction honeypot and θ satisfying the Eq.(9),1ν would be the dominant strategy for attackers.In this case, attackers will launch offensive access.Otherwise,2ν would be the dominant strategy for attackers and attackers will not launch offensive access to the low-interaction honeypot.Similarly, when the service provider is a high-interaction honeypot and θ satisfying the Eq.(10),1ν would be the dominant strategy for attackers.In this case, attackers will launch offensive access.Otherwise,2ν would be the dominant strategy for attackers and attackers will not launch offensive access to high-interaction honeypot.Considering that the players in this game should choose the dominant strategy, we can obtain the dominant strategy (ν1,ν1) for SP, which is their strategy (Ω1, Ω1)under the condition Eq.(9) and Eq.(10).

Now, we further prove the dominant strategy of attackers when the SP use strategy (Ω1, Ω1).First, we need to check whether the strategy (Ω1, Ω1)is the dominant strategy or not from the perspective of SP.Assuming that UZ1( Ω1)＞UZ1( Ω2)and UZ2( Ω1)＞UZ2( Ω2),

we have consider the case when θ satisfies the Eq.(9) and Eq.(10), the Eq.(11) and Eq.(12) hold true because the value of function 0＜Ψi＜ 1 .In this case, we know that the relations(1-α)*(1-Ψ1)*β +α*(1- Ψ3)*β＞ 0 and (1-α)*(1-Ψ2)*β +α*(1-Ψ4)*β＞ 0 are always hold true, so it is obvious that the SP strategy Ω1will be the dominant strategy for attackers’ strategy(ν1,ν1).Similarly, when offensive access is strong offensive access, the SP strategy Ω1will be always the dominant strategy for attackers’ strategy(ν1,ν1).In summary, from Eq.(9), Eq.(10), Eq.(11) and Eq.(12), we can obtain a Bayesian-Nash Equilibria (BNE) (ν1,ν1, Ω1, Ω1)for the LHHG and Theorem I can be proved.

Analogously, three other BNE strategies(ν1,ν2, Ω1, Ω1),(ν2,ν1, Ω1, Ω1), and (ν2,ν2, Ω1, Ω1)exist in the game under other conditions we discussed before.When there are sufficient human analysis costs, the Bayesian-Nash strategies for the LHHG model can be reached from Algorithm 1.

Algorithm 1: Bayesian-Nash strategy for low-high interaction honeypot game model Input: 121212341234, , , , , , , , , , , , , p p p p a a a an and ς ς γ γαθ Output: Optimal strategy (), , ,iijjiijj ν ν Ω Ω /* Initialize the strategy, (),iijj ν ν */ /* Find the stable state*/ if 1122111()0 θςςς γ Ψ -Ψ+Ψ - ≥ then if 4231312()0 θςςς γ Ψ -Ψ+Ψ - ≥ choose optimal strategy 1111( , , ,)ν ν Ω Ω else choose optimal strategy 1211( , , ,)ν ν Ω Ω end else if 4231312()0 θςςς γ Ψ -Ψ+Ψ - ≥ choose optimal strategy 2111( , , ,)ν ν Ω Ω else choose optimal strategy 2211( , , ,)ν ν Ω Ω end end

4.2 The optimal defensive strategy with insufficient human analysis cost

In the last subsection, we derive the BNE for attackers and SP with sufficient analysis resources.However, in real scenarios, the SP usually faces the budget shortage for operation and maintenance of honeypots, which decreases the real operation performance.Therefore, it is necessary to consider the operation cost constraint to find the optimal defensive strategy.In practice, if the generated reports are not analyzed or not activated by the human, the function of a honeypot is nearly equivalent to a normal server.Therefore, human analysis cost is a vital factor for the effective operation of honeypots, and it is necessary to consider accurate in this paper.When the SP's total human analysis cost satisfies the requirement for honeypots in the aforementioned BNE, all honeypots can work well.In contrast, if the SP has insufficient human analysis cost, some of the honeypots may not work effectively due to the lack of the participation of human.Therefore, it is very necessary to study how to improve the capture performance of the honeypot system under the constraint of insufficient human analysis cost.Moreover, the payoff expression is shown below.

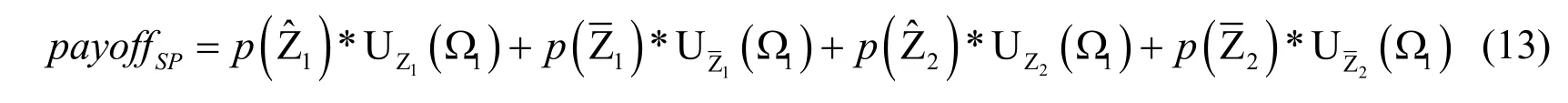
We define the human analysis cost required for a low-interaction honeypot and a highinteraction honeypot is lc and hc, respectively.We also define the average human analysis cost constraint for a honeypot asC.For the SP, maximizing the payoff means minimizing the loss.Therefore, a reasonable allocation of insufficient human analysis costs is important to achieving an optimal defense strategy after the honeypots are deployed.Furthermore, the optimal human analysis cost allocationcan obtained by solving the optimization problem of the following expression:

Obviously, the Eq.(16) expresses a nonlinear inequality constrained optimization problem, whereis a list of variables and Eq.(17) is constraint.Through the research of payoff expression, the properties of expression is a monotone increasing function of variableTherefore, the optimal solution of Eq.(16) is usually lies on the boundary of the feasible domain.In order to solve the optimization problem, here, we introduce UP as an evaluation factors.UP indicates the unit human analysis cost payoff.Furthermore, the expression of UP can be obtained from the analysis in the subsection above and expressed below.

Eq.(18) and Eq.(19) indicate the unit human analysis cost payoff for low- and highinteraction honeypot, respectively.We can obtain the optimal human analysis cost allocation through the following ways: if UPz1is greater than UPz2, we tend to allocate more human analysis cost to low-interaction honeypots at first.By contrast, if UPz2is greater than UPz1, we tend to allocate more human analysis cost to high-interaction honeypots at first.

To this end, to integrate the strategy of the previous part, the optimal defensive strategy consists of two parts: the optimal deployment of low- and high-interaction honeypots and the optimal allocation of insufficient human analysis cost.

5 Simulations

In this section, we carry out numerical simulations in which different ratio of unit human analysis cost of the low- and high-interaction honeypot are adopted, in order to evaluate the effects of human analysis cost.The details of the simulation settings are explained first, and simulation results are given later.

5.1 Simulation settings

We conduct various simulations to explore the appropriate human analysis cost allocation of high-interaction honeypots and low-interaction honeypots for capturing network attacks in the honeypot network.In our simulation, we adopt one typical BNE (ν1,ν1, Ω1, Ω1)as the strategy for attackers and SP.Under this BNE strategy, the attacker launches both strong and weak offensive access, while the SP requires both high- and low-interaction honeypots to provide service.

In order to verify the significance of human analysis cost constraint in defensive strategy, we consider one situation that the performance of high-interaction honeypot is better than low-interaction honeypot and adopt low-interaction honeypot escape probabilities of (0.5, 0.6).In this situation, the escape probabilities of the combinations of the low- and high- interaction honeypots are (p1, p2, p3, p4)= (0.5,0.4,0.7,0.6).In addition, the minimum escape probabilities are assumed as (a1, a2, a3, a4)= (0.2,0.15,0.3,0.25); the rewards of low-interaction honeypot and the high-interaction honeypot are assumed as (ς1, ς2) =(30,50); the cost of weak offensive access and strong offensive access is assumed as(γ1, γ2) =(3,6)and the reward of CPS working normally is assumed asβ =1000.Obviously, the human analysis cost of high-interaction honeypot and lowinteraction honeypot is different.However, when C＜ (1 -θ)lc, the human analysis cost is not enough for a low-interaction honeypot, and all honeypots will not work.Therefore, we consider the case θhc ≥ C≥ (1 -θ)lc andIn addition, considering the generic condition of generic functionwe assumed one simple case as follows:

In particular, when there is only one high-interaction honeypot or low-interaction honeypot, Ψi= piand ki= 1-ai/pi.

We investigate the properties of the functionvia adopting four sets of parameters ki, pi,ai.As shown in Fig.3, as the number of deployed honeypots increases, the escape probability of strong and weak offensive access decreases and asymptotically tends to the minimum escape probability.This property is consistent with the theoretical prediction.In addition, it is obvious that when the human analysis cost is sufficient, the payoff of SP is greater than the human analysis cost is insufficient.This is because those honeypots, which are not allocated human analysis costs, do not have capture effects.Therefore, it is necessary to study the human analysis cost allocation.

Figure 3: The escape probability of weak offensive access and strong offensive access

In order to obtain the optimal defensive strategy, we study one typical BNE (ν1,ν1, Ω1, Ω1)below.We first assume that the optimal deployment of low- and high-interaction honeypot is θ =0.5 according to the Eq.(9) and Eq.(10).Then, we verify how to obtain the optimal human analysis cost allocation under different human analysis cost ratio of a high- and low-interaction honeypot hc /lc according to the method of Eq.(18) and Eq.(19) when the probability of strong offensive access α =0.5is fixed.Finally, we compare the payoff of SP under different hc /lc.In addition, we assume that the total number of honeypots is 40.

5.2 Simulation results

In order to verify the method, we proposed before, extensive numerical simulations are performed.According to the assumption, we have the Eq.(18) and Eq.(19) as follows:

Obviously, it is hard to compare the value of UPZ1and UPZ2.Therefore, in order to analyze the difference between the UPZ1and UPZ2, we investigate them at different values of hc /lc in the numerical simulation via MATLAB, as shown in Fig.4(a).

In Fig.4(a), the abscissa indicates /hc lc,which is the ratio of the human analysis cost of the high-interaction honeypot to that of the low-interaction honeypot.The ordinate represents the unit human analysis cost payoff.Obviously, when the hc /lc increases, the unit human analysis cost payoff of high-interaction honeypot decreases and convex.Particularly, if hc /lc ＜1.569, the SP tends to allocate more human analysis costs to the high-interaction honeypot.In contrast, if hc /lc ＞1.569, the SP tends to allocate more human analysis costs to the low-interaction honeypot.In addition, we compare the difference in the payoff of SP under the condition of sufficient human analysis cost, and analyze the impact of human analysis cost constraints in Fig.4(b).

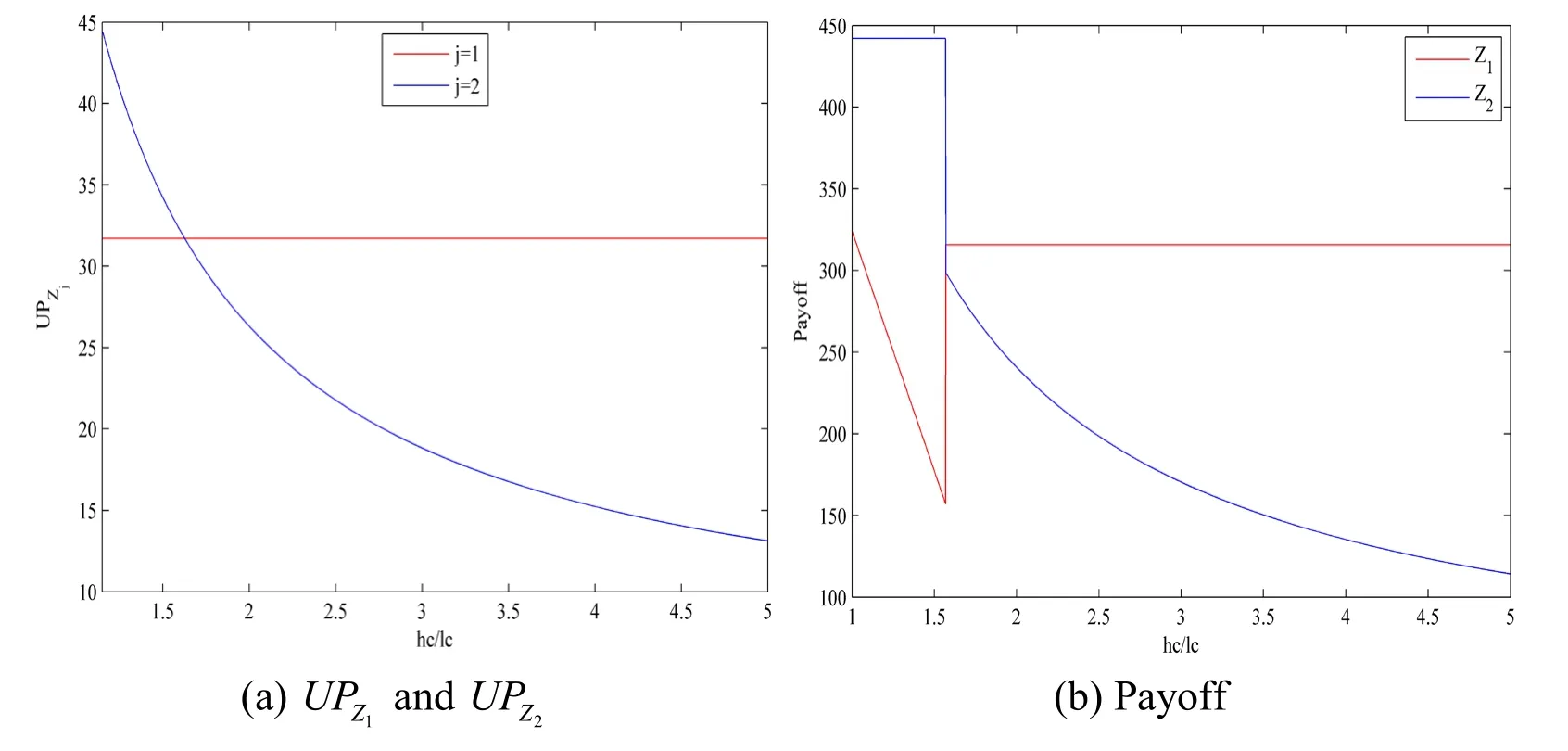
Figure 4: The UPZ1 and UPZ2 and payoff of low- and high-interaction honeypots as a function of hc /lc

In Fig.4(b), the ordinate represents the payoff.Obviously, when the hc /lc increases, the payoff of high-interaction honeypots inclines to stable firstly and then decreases and convex.When hc /lc ＜1.569, we prioritize the allocation of human analysis costs to high-interaction honeypots.In contrast, the payoff of low-interaction honeypots decreases first and then step and inclines to stable.We find that when hc /lc ＞1.569, the human analysis cost is prioritized for low-interaction honeypots and the payoff of lowinteraction inclines to stable.In addition, this is also the case in an earlier study between the UPZ1and the UPZ2that further validate the effectiveness of our method.

Thus, take hc /lc= 3 as an expample, the optimal defense strategy is to deploy half lowinteraction honeypots and half high-interaction honeypots and prioritize human analysis costs for high-interaction honeypots.The payoff of SP is 475.3744 in this case.

In summary, the investigation of the human analysis cost allocation of the high- and the low-interaction honeypot shows the optimal defensive strategy can be achieved via combining the optimal deployment strategy.

6 Conclusion

In this paper, we propose a honeypot game model with both low- and high-interaction modes to improve the security of cyber-physical systems (CPS), an advanced system integrating physical processes, computation and communication resources.To optimize defensive strategies against network attacks in CPS, an analysis resource constraint is introduced.With the low- and high-interaction honeypots as a security management tool deliberately designed to be probed, attacked and compromised, we study the offensive and defensive interactions of CPS and model the offensive and defensive process as an incomplete information game with the assumption that the defender's analysis resource is unknown to the attacker.Firstly, we prove the existence of several Bayesian-Nash equilibria in the low- and high-interaction honeypot game without analysis cost constraints and obtain the attacker's equilibrium strategy.Then, we take the impact of analysis cost on the capture effect of honeypots into consideration and further optimize the defensive strategy by allocating analysis resource between low- and high-interaction honeypot with resource constraint.Finally, Numerical simulation results showed that the optimal human analysis cost allocation and optimal defensive strategy can be obtained based on our analysis, which indicates that our method can be used to protect the data and to further ensure the security of CPS.

Acknowledgement:This work was supported by The National Natural Science Foundation of China (Grant No.U1836104, U1636117, 61602247, 61702235), Natural Science Foundation of Jiangsu Province (Grant No.BK20160840).

References

Alata, E.; Nicomette, V.; Kaaniche, M.; Dacier, M.; Herrb, M.(2006): Lessons learned from the deployment of a high interaction honeypot.Proceedings of the Sixth European Dependable Computing Conference, pp.39-46.

Amin, S.; Schwartz, G.A.; Hussain, A.(2013): In quest of benchmarking security risks to cyber-physical systems.IEEE Network, vol.27, no.1, pp.19-24.

Banerjee, A.; Venkatasubramanian, K.K.; Mukherjee, T.; Gupta, S.K.S.(2012): Ensuring safety, security, and sustainability of mission critical cyber physical systems.Proceedings of the IEEE, vol.100, no.1, pp.283-299.

Cao, A.J.; Liu, B.X.; Xu, R.S.(2004): Summary of the honeynet and entrapment defense technology.Computer Engineering, vol.30, no.9, pp.1-3.

Celli, G.; Pegoraro, P.A.; Pilo, F.; Pisano, G.; Sulis, S.(2014): DMS cyber-physical simulation for assessing the impact of state estimation and communication media in smart grid operation.IEEE Transactions on Power Systems, vol.29, no.5, pp.2436-2446.

Cohen, F.(1998): Special feature: a note on the role of deception in information protection.Computers & Security, vol.17, no.6, pp.483-506.

Faisal, M.A.; Aung, Z.; Williams, J.R.; Sanchez, A.(2015): Data-stream-based intrusion detection system for advanced metering infrastructure in smart grid: A feasibility study.IEEE Systems Journal, vol.9, no.1, pp.31-44.

Ghourabi, A.; Abbes, T.; Bouhoula, A.(2013): Automatic analysis of web service honeypot data using machine learning techniques.International Joint Conference CISIS'12-ICEUTE' 12-SOCO' 12 Special Sessions, pp.1-11.

Hastings, J.; Laverty, D.M.; Morrow, D.J.(2014): Tracking smart grid hackers.49th International Universities Power Engineering Conference, pp.1-5.

Hodo, E.; Bellekens, X.; Hamilton, A.; Dubouilh, P.L.; Iorkyase, E.et al.(2016): Threat analysis of IoT networks using artificial neural network intrusion detection system.International Symposium on Networks, Computers and Communications, pp.1-6.

Humayed, A.; Lin, J.Q.; Li, F.J.; Luo, B.(2017): Cyber-physical systems security-a survey.IEEE Internet of Things Journal, vol.4, no.6, pp.1802-1831.

Koscher, K.; Czeskis, A.; Roesner, F.; Patel, S.; Kohno, T.et al.(2010): Experimental security analysis of a modern automobile.IEEE Symposium on Security and Privacy, pp.447-462.

Levine, J.; LaBella, R.; Owen, H.; Contis, D.; Culver, B.(2003): The use of honeynets to detect exploited systems across large enterprise networks.IEEE Systems, Man and Cybernetics Society, Information Assurance Workshop, pp.92-99.

Li, Y.F.; Zhang, L.; Zheng, H.; He, X.Z.; Peeta, S.et al.(2017): Nonlane-disciplinebased car-following model for electric vehicles in transportation-cyber-physical systems.IEEE Transactions on Intelligent Transportation Systems, vol.19, no.1, pp.38-47.

Liu, W.Y.; Luo, X.Y.; Liu, Y.M.; Liu, J.Q.; Liu, M.H.et al.(2018): Localization algorithm of indoor Wi-Fi access points based on signal strength relative relationship and region division.Computers, Materials & Continua, vol.55, no.1, pp.71-93.

Mohi, M.; Movaghar, A.; Zadeh, P.M.(2009): A Bayesian game approach for preventing DoS attacks in wireless sensor networks.2009 WRI International Conference on Communications and Mobile Computing, pp.507-511.

Mukkamala, S.; Yendrapalli, K.; Basnet, R.; Shankarapani, M.K.; Sung, A.H.(2007): Detection of virtual environments and low interaction honeypots.Information Assurance and Security Workshop, pp.92 - 98.

Nappa, A.; Johnson, R.; Bilge, L.; Caballero, J.; Dumitras, T.(2015): The attack of the clones: A study of the impact of shared code on vulnerability patching.IEEE Symposium on Security and Privacy, pp.692-708.

Nawrocki, M.; Wahlisch, M.; Schmidt, T.C.; Keil, C.; Schonfelder, J.(2016): A survey on honeypot software and data analysis.https://arxiv.org/pdf/1608.06249.pdf.

Pasqualetti, F.; Dorfler, F.; Bullo, F.(2013): Attack detection and identification in cyber physical systems.IEEE Transactions on Automatic Control, vol.58, no.11, pp.2715-2729.

Provos, N.(2004): A virtual honeypot framework.USENIX Security Symposium, vol.173, pp.1-14.

Spitzner, L.(2003): Honeypots: Tracking Hackers.Addison-Wesley.

Stoll, C.(1989): The Cuckoo’s Egg: Tracking A Spy Through the Maze of Computer Espionage.Simon and Schuster.

Vetsch, S.(2011): Glastopfng: A Web Attack Honeypot.VDM Verlag.

Von Solms, R.; Van Niekerk, J.(2013): From information security to cyber security.Computers & Security, vol.38, no.10, pp.97-102.

Wang, K.; Du, M.; Maharjan, S.; Sun, Y.F.(2017): Strategic honeypot game model for distributed denial of service attacks in the smart grid.IEEE Transactions on Smart Grid, vol.8, no.5, pp.2474-2482.

Wang, K.; Ouyang, Z.Y.; Krishnan, R.; Shu, L.; He, L.(2015): A game theory-based energy management system using price elasticity for smart grids.IEEE Transactions on Industrial Informatics, vol.11, no.6, pp.1607-1616.

Yağan, O.; Qian, D.J.; Zhang, J.S.; Cochran, D.(2012): Optimal allocation of interconnecting links in cyber-physical systems: Interdependence, cascading failures, and robustness.IEEE Transactions on Parallel & Distributed Systems, vol.23, no.9, pp.1708-1720.

Yang, J.; Zhou, C.J.; Yang, S.H.; Xu, H.Z.; Hu, B.W.(2018): Anomaly detection based on zone partition for security protection of industrial cyber-physical systems.IEEE Transactions on Industrial Electronics, vol.65, no.5, pp.4257-4267.

Zang, W.Y.; Liu, P.; Yu, M.(2007): How resilient is the internet against DDoS attacks a game theoretic analysis of signature-based rate limiting.International Journal of Intelligent Control and Systems, vol.12, no.4, pp.307-316.

Zhang, F.; Zhou, S.J.; Qin, Z.G.; Liu, J.D.(2003): Honeypot: A supplemented active defense system for network security.Proceedings of the Fourth International Conference on Parallel and Distributed Computing, Applications and Technologies, pp.231-235.

Zhuge, J.W.; Holz, T.; Han, X.H.; Song, C.Y.; Zou, W.(2007): Collecting autonomous spreading malware using high-interaction honeypots.International Conference on Information and Communications Security, pp.438-451.