An Auto-Calibration Approach to Robust and Secure Usage of Accelerometers for Human Motion Analysis in FES Therapies

Mingxu Sun , Yinghang Jiang Qi Liu and Xiaodong Liu

Abstract: A Functional Electrical stimulation (FES) therapy is a common rehabilitation intervention after stroke, and finite state machine (FSM) has proven to be an effective and intuitive FES control method.The FSM uses the data information generated by the accelerometer to robustly trigger state transitions.In the medical field, it is necessary to obtain highly safe and accurate acceleration data.In order to ensure the accuracy of the acceleration sensor data without affecting the accuracy of the motion analysis, we need to perform acceleration big data calibration.In this context, we propose a method for robustly calculating the auto-calibration gain using redundant acceleration vectors, and then calibrating the data generated by the accelerometer based on the calculated gain.The selection of the acceleration vector involved in the gain calculation is demonstrated by different experiments.The results show that the auto-calibration gain calculated after calibration is very close to 1, and the error is significantly less than before calibration, which indicates that the accelerometer unit is well calibrated.

Keywords: Data calibration, accelerometer data analysis, functional electrical stimulation, stroke therapy.

1 Introduction

With the development of medical technology and the continuous improvement of people’s living standards, the number of elderly people is rising, and there are a large number of stroke patients in the aging population.Stroke is a disease with a high mortality rate.Survivors are accompanied by varying degrees of functional impairment and limited mobility.They may lose their ability to control their arms.They cannot perform normal daily life, and some may even have permanent disabilities [Jiang, Xiong, Sun et al.(2011)].Their quality of life has had a serious impact.Without systematic training, it is difficult for patients to recover.Therefore, it is necessary to carry out rehabilitation training for stroke patients.Functional Electrical stimulation (FES) therapy is a common post-stroke rehabilitation intervention designed to help patients recover their upper limb motor control function.However, it is very challenging to achieve satisfactory control of muscle responses to stimuli [Ferrarin, Palazzo, Riener et al.(2001)].Based on the effectiveness and timeliness of smart medical care, the clinicians can positively impact the quality and cost of medical care [Fang, Cai, Sun et al.(2018)].FSM (finite state machine) has been proved to be an effective and intuitive FES control method [Tresadern, Thies, Kenney et al.(2008)].FSM controllers use sensors on the body to switch between states to achieve control of electrical stimulation.Modern accelerometers have many advantages, such as low cost, small size, easy to wear and so on [Nez, Fradet, Laguillaumie et al.(2016)].FSM can use the data information generated by the accelerometers to trigger the state transition robustly.In the medical field, it is necessary to obtain highly accurate acceleration data [Godfrey, Conway, Meagher et al.(2008)].The correlation of human motion analysis results directly depends on the accuracy of the collected data.

However, the use of accelerometer may bring some problems, such as the sensitivity of accelerometer in use may decline, or the accumulation of errors, resulting in data drift, in order to ensure that the sensor work in line with technical specifications, does not affect the accuracy of motion analysis, we need to calibrate the accelerometer.At present, there are two main methods for accelerometer calibration: the first one relies on high-precision external equipment, such as turntable, for accurate calibration, the main calibration installation error, proportional coefficient and zero offset, mostly used for laboratory calibration.This method is called the "6-position method".It requires a high-precision device, and must ensure that the coordinate system of the device coincides with the coordinate system of the accelerometer [Titterton and Weston (2004); Cai, Song, Yang et al.(2013)].Then it is tested vertically and downward along the sensitive axis of the accelerometer, as shown in Fig.1 [Nez, Fradet, Laguillaumie et al.(2016)].Then, the least squares method is used to estimate the calibration parameters for minimum error estimation of the 6-position data.6 position method is simple and practical, but the implementation has great limitations.It is necessary to align the acceleration axis with the vertical axis as far as possible, otherwise the calibration accuracy will be affected.In addition, most laboratories do not have professional equipment, so the calibration is difficult [Syed, Aggarwal, Goodall et al.(2007)].The second method is called fitting calibration.This method does not need other equipment, and is more suitable for various fields.This method collects a series of off-line acceleration data.According to the theorem, the measured acceleration modulus is always the local gravity acceleration in the case of static placement.Calibration parameters can be easily calculated using computers.

In this paper, we adopt the fitting calibration method, and then optimize it.We use the redundant acceleration vector to calculate the gain robustly (i.e., the compensation parameter).In the process of calculating the gain, we eliminate the bad acceleration vector which affects the calibration accuracy, and select the acceleration number under four different conditions.According to the experiment, the influence of these conditions on the gain calculation is compared, and the acceleration error before and after calibration is analyzed.The experiment proves that the output of the calibrated accelerometer data is closer to the gravity acceleration, and the error between the calibrated accelerometer data and the gravity acceleration is smaller.

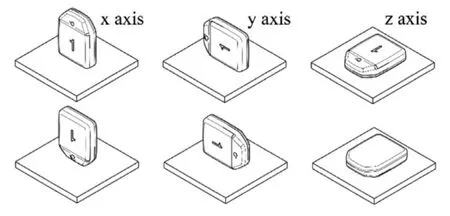
Figure 1: 6-position method (Nez A et al.[Nez, Fradet, Laguillaumie et al.(2016)])

2 Related work

The root cause of stroke disability is that the patient’s central nervous system is damaged, so that the limb movement cannot be effectively controlled, resulting in partial loss of limb behavior.The function of the bones and muscles of the patient's limbs has not been lost.In order to prevent hemiplegia, there are many rehabilitation methods, including electromyography biofeedback, constraint-induced movement therapy (CIMT), roboticassisted therapy, functional electrical stimulation, mental practice with motor imagery, etc.[He and Wang (2014)].

Electromyography biofeedback.Electromyography biofeedback is an application of an electromyography biofeedback device to amplify the physiological activity of muscle tissue that people are not aware of, and convert it into visual and auditory signals that can be perceived by people, and pass these signals through eyes, ears, etc.The organs are returned to the brain so that the human body can independently train according to these signals to control the bioelectric activity of the muscle tissue for training purposes.Some studies have shown that it is an effective adjuvant therapy, and it is also one of the hotspots of research at home and abroad [He, Hua, Luo et al.(2017)].However, different studies use different treatment prescriptions and evaluate the efficacy in different ways, and each treatment lacks the evidence of basic research, and there is not enough data to show that EMG biofeedback therapy has significant benefits in improving upper limb function.There is also a limited effect of electromyography biofeedback therapy on improving the range of motion of the wrist.

Constraint-induced movement therapy.CIMT is one of the most influential rehabilitation technologies in the past 20 years, and has been greatly developed at home and abroad and has received extensive attention.It improves the motor function of the limbs by restricting the movement of the limbs and forcing the limbs to perform a large number of intensive training, thereby improving the motor function and activities of daily living of patients with hemiplegia due to cerebral infarction.Professor Taub proposed CIMT.The multi-center clinical study in the United States confirmed that CIMT is the most effective rehabilitation technique for improving upper extremity motor function, especially for patients with hemiplegia and upper extremity motor dysfunction in convalescence stroke [Taub, Uswatte, King et al.(2006); Taub, Crago and Uswatte (1998)].However, the applicability of CIMT is limited.For example, it is not suitable for widespread use in the acute phase of stroke.In addition, CMIT is expensive because it requires the time of the therapist and the resources of the rehabilitation department.

Robotic-assisted therapy.With the development of artificial intelligence technology, rehabilitation robot technology has also made great progress in recent years.Robotic assisted therapy is the use of mechanical devices to provide or support high-intensity and controllable repetitive upper limb exercises.Stanford University has developed the MIME (mirror image motion enabler) system based on PUMA500 and 560 industrial robots (Fig.2) [Lum, Burgar and Shor (2003); Burgar, Lum, Shor et al.(2003)].In addition, compared with traditional exercise therapy, robotic adjuvant therapy seems to be easier to be Patient approval [Kwakkel, Kollen and Krebs (2008)].Liang et al.'s research shows that there are still some shortcomings in upper limb rehabilitation robots, such as the inability to perform flexion and extension training of wrist joints, the system's own joint range estimation system and the actual measured value error of the protractor are large [He and Wang (2014)].Although the upper limbs Rehabilitation robot technology has made great progress in research at home and abroad, but the current research is still in its infancy, one robot is expensive and has no universality; the other is the lack of large-sample clinical application and research.

Mental practice with motor imagery.Mental practice with motor imagery, also known as mental imaging, refers to consciously simulating and training an action through the brain without accompanying obvious physical or physical activity.Through long-term simulated imaginary exercise training, non-conditioned reflexes are transformed into conditioned reflexes.Neurological function and innervation of muscle function, thereby improving the damaged "sports network" and achieving the goal of exercise imaging training [Fu, Chen, Yu et al.(2010)].However, the largest research to date, Letswaart, Johnston et al [Ietswaart, Johnston, Dijkerman et al.(2011)].A total of 121 stroke patients with residual upper extremity weakness (mean ＜3 months after stroke) were examined and no improvement in outcome measurements was found.Therefore, there is no clear evidence that the psychological practice of motor imaging technology can improve motor function and facilitate the recovery of stroke in isolation.

Functional electrical stimulation.FES is an effective method for treating hemiplegia in stroke patients.A large number of clinical studies have shown that electrical stimulation therapy can significantly improve the limb function of patients with stroke and improve the limb control ability of patients.Popovic et al.used FES to treat acute stroke patients with hemiplegia.After 3 weeks of treatment, the affected arm function was effectively improved [Popovic, Popovic, Sinkjaer et al.(2004)].Chen et al.used FES to stimulate the forearm wrist extensor muscle group to produce wrist extension, after treatment.Wrist flexion and extension function and hand coordination activities have improved significantly, indicating that FES treatment can improve the motor function of the hand, and FES has a more positive effect on the improvement of arm function [Lin and Chen (2010)].

In summary, we can get the comparison results, see Tab.1, FES has fewer shortcomings and is more suitable for helping patients to recover upper limb motor control after stroke.Therefore, we use FES to perform rehabilitation training on upper limb control function of stroke patients.

Figure 2: Use assisted robots to help patients with rehabilitation training

However, achieving a satisfactory level of FES control is very challenging.In order to better control the FES to make full use of it, the designers developed the FES control system using the sensor.The FES can be used as a feedback source to control the stimulus.The common sensors used in the FES system include the force sensor, the position sensor and the acceleration sensor.The sensor is typically used to provide a feedback signal in the FES system, and the controller can use the data information generated by the acceleration sensor to robustly trigger state transitions.In the medical field, highly accurate acceleration data is required to ensure the safety of the system.Calibration is a very effective way to improve the accuracy of the data collected from the three-axis accelerometer, so we need to calibrate the accelerometer.At present, accelerometer calibration methods mainly include:

1.6-position accelerometer calibration method: Zhang et al.[Zhang and Ye (2009)] adopted a 6-position accelerometer calibration method, which is easy to implement, simple and easy to implement, and does not require external equipment assistance in actual use, but the method has low precision and is not suitable for medical treatment.field.

2.External device calibration method: relying on high-precision external equipment, such as turntables, for accurate calibration, main calibration installation error, scale factor and zero offset, mostly used for calibration in the laboratory, there are equipment restrictions.

3.Kalman Filtering: Jafari et al.[Jafari, Sahebjameyan, Moshiri et al.(2015)] used dual Kalman filtering, which is an excellent tool for data fusion from noise signals, calibrating MEMS gyros and accelerometers, respectively, and using modeling methods to minimize prediction errors for Kalman the zero-bias stability and random walk noise in the filter are modeled, but the algorithm is computationally complex and different filter parameters need to be set for different sensors [Liu, Li, Di et al.(2018)].

4.Dynamic and static inertial measurement: Liu et al.[Liu and Fang (2008)] adopts an improved dynamic and static inertial measurement system (INS) high-precision calibration method.Although the accuracy is improved, the method needs to be assisted by external precision equipment (calibration turntable).In this case, this method cannot be used for accurate calibration.In order to make the calibration of FES controller accelerometer more convenient and accurate, this paper adopts the method of fitting calibration, and optimizes it based on this, and proposes a method to calculate the automatic calibration gain robustly by using redundant acceleration vector.Then, the data generated by the acceleration sensor is calibrated according to the calculated gain.

Table 1: Comparison of FES with other treatment options

3 Methodology

Because the 6-position calibration method requires a well-designed instrument, this method is only suitable for in-lab calibration.In order to break through the limitations of the instrument, Lötters et al.[Lötters, Schipper, Veltink et al.(1998)].proposed an initial method that does not require any alignment equipment and is suitable for any type of accelerometer calibration.The method is based on the following theorem.In the case of static placement, the measured acceleration modulus is always Local gravity acceleration:

The method proposed in this paper is also based on the theorem.

3.1 Model

Ideally, the accelerometer will have exactly the same sensitivity anywhere within the specified amplitude range.It is generally accepted that models can be considered to be linear.Establish a numerical model, assuming the measured values are [axmaymazm]T, the calibrated values are [axcaycazc]T,the translation parameters are [fxfyfz]T, the scaling parameters are [kxkykz]T, then the model is:

The calibrated acceleration is linked to the original acceleration reading by six calibration parameters (three scale factors and three offsets).The model is based on a restrictive assumption: the three axes of the accelerometer are perfectly orthogonal.

Due to the inaccurate structure of the three-axis accelerometer, the three axes cannot be completely orthogonal, we use T to represent the transformation matrix of the axis deviation:

To further simplify the transformation matrix T, we assume that the x-axis of the reference coordinate system coincides with the x-axis of the accelerometer's actual rotating coordinate system, and the y-axis of the reference frame is in the plane of the x-axis and the y-axis of the actual rotation coordinate system of the accelerometer.So, the transformation matrix can be further written as follows:

such that the model becomes:

where acis the calibrated acceleration, Tais the transformation matrix of the axis deviation, S is the scale factor, amis the acceleration reading, b is the offset.The factor can be replaced by a new matrix k whose factor depends on the non-orthogonal, acceleration sensitivity of the axis.

3.2 Calculates auto-calibration gains

The auto-calibration gain of each sensitive axis can be calculated using Eqs.(6) -(8) below.We need at least 3 acceleration vectors to solve the following equation: (g selects the local gravity acceleration of Nanjing 9.79 m/s2[Baidu Document (2018)])

Where kx, kyand kzare the automatic calibration gains for each sensitive axis respectively, ax, ayand azare the accelerometer readings before calibration.

In order to be able to calculate the calibration gain robustly, we use a redundant acceleration vector to calculate.When we use more acceleration vectors instead of 3, for example when using 9 vectors, (which will explain how to select the acceleration vector in the third part) we will get the following equation:

Next, we use the pseudo-inverse method to solve the above equation to get Eq.(10):

Finally, calculate the calibration gain (kx2, ky2and kz2) according to Eq.(10).

3.3 Calculates auto-calibration errors

We use the least squares error model to calculate the error of the auto-calibration gain for each accelerometer’s sensitive axis, calculated by Eqs.(11)-(12) below:

where ε1-ε9are the ca lculated errors for when applies a set of calculated auto-calibration gains for each linear equations.

Where, εsumis the sum of errors (ε1-ε9).

4 Experiments

In this section, we will use the above methods to select different acceleration data sets for experiments.Before the calibration, the acceleration sensor readings should be close to the gravitational acceleration when static.Therefore, the calculated gain should be approximately equal to one.We use the following steps to experiment with different acceleration vectors for different data sets:

1.Move the sensor along 3 axes to collect 5 seconds of acceleration data;

2.Select 9 acceleration vectors in different ways, select eight fixed points, the ninth point is the moving point, and calculate data for each group of nine;

3.Calculate the gain and error of each group;

4.Calculate the automatic calibration gain after removing the bad acceleration vector;

5.Compare the gain calculated before and after the bad acceleration vector is removed.

Acceleration data when moving the acceleration sensing unit along the x, y, and z axes is collected (see Fig.3).The dashed vertical line represents the eight acceleration vectors that calculate the auto-calibration gain.The ninth acceleration vector is moved from the first acceleration reading in the above figure to the last acceleration reading.These 9 acceleration vectors are combined to calculate the gain.

Calculated auto-calibration gains when different ninth acceleration vectors obtained (see Fig.4).

Then calculate the sum of the errors of the different ninth acceleration vectors.

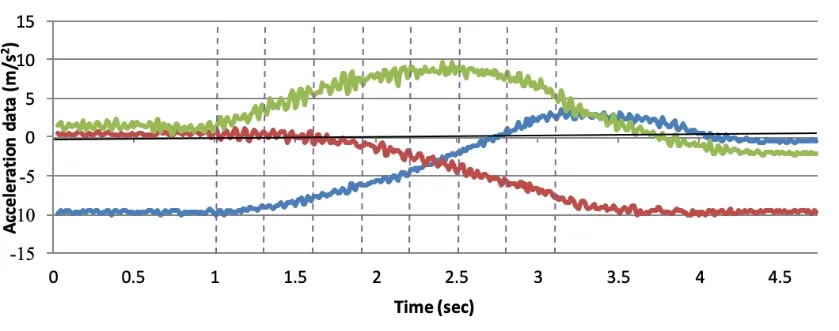
Figure 3: Acceleration data when moving the acceleration sensing unit along the x, y, and z axes is collected

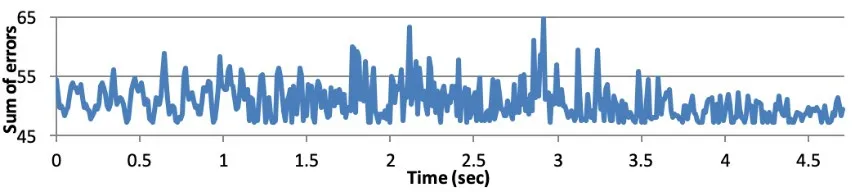
Figure 5: Sum of the errors of the different ninth acceleration vectors

As can be seen from Fig.5, there is a large error in some points, which we can think is due to the existence of a bad acceleration vector.The bad acceleration vector is generated by signal noise or when the acceleration sensor is moved with a large acceleration.Next, we remove the bad acceleration vector and compare the gain changes between the two.We have developed a rejecting rule: set a threshold, which is the best guess from the average of the initial partial error readings.When the error is greater than the threshold, we consider this a bad acceleration vector.Fig.6 shows the auto-calibration gain after rejecting the bad acceleration vector (bad calculation is when sum of errors greater than 51.15, this is the average from first 80 readings).

Figure 6: The auto-calibration gain after rejecting the bad acceleration vector

Table 2: Gain and standard deviation comparison

Tab.2 shows the gain and standard deviation of each axis of the acceleration sensor before and after the bad vector is removed.

We can see that after eliminating the bad acceleration vector, the standard deviation is significantly smaller than the unremoved, so that we can get the auto-calibration gain more accurately.

In the following experiment, we used the same data set as the previous experiment.When we selected eight acceleration vectors, we let them have no significant separation, as shown in the vertical dotted line in Fig.7.The same as above dashed vertical line represents the eight acceleration vectors that calculate the auto-calibration gain.The ninth acceleration vector is moved from the first acceleration reading in the above figure to the last acceleration reading.

Figure 7: Select the eight acceleration vectors without significant separation

Calculated auto-calibration gains when different ninth acceleration vectors obtained (see Fig.8).

Figure 8: Calculate the auto-calibration gain for each group

Calculate the sum of the errors of the different ninth acceleration vectors (see Fig.9).

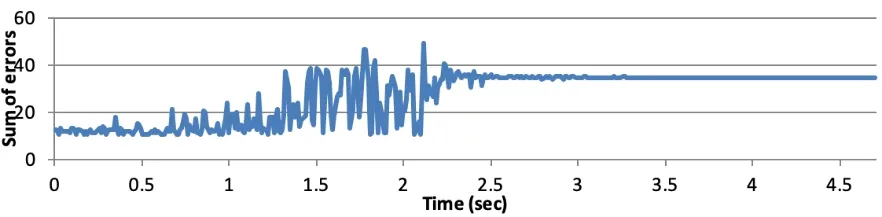
Figure 9: Sum of errors (εsum) when different ninth acceleration vectors

From Fig.9, we can see that this may cause a portion of the error when the selected acceleration vector is not significantly separated.This is because if many selected acceleration vectors (each acceleration vector is a linear equation, e.g., kx2ax12+ky2ay12+kz2az12=(9.79m/s2)2) are closed to each other (see dash vertical lines in Fig.9).The errors εn(n=1-9) for a set of calculated auto-calibration gains applied to those closed linear equations might be all small.This will lead to an overall small sum of error.In addition, those acceleration vectors (linear equations) will be more likely to be linear dependent to each other.

When there is another g vector, which is separated from those closed g vectors, obtained for the calculation (see Fig.7 when ninth acceleration vector moves from 2.5 seconds), this may lead to a big increase to the sum of errors (see Fig.9 from 2.5 seconds).A possible explanation to this is, the errors εn(n=1-9) for a set of calculated auto-calibration gains applied to those closed linear equations increasing at a same time.Therefore, we propose that in this automatic calibration method, when the acceleration sensing unit rotates, all acquired acceleration vectors should be separated from each other in space.

When there is a calibration phase, we move the acceleration sensing unit around the X, Y, and Z axes and pause for ＞1 second when the x-axis is in different quadrants of space, and get the first 8 acceleration vectors when the acceleration sensing unit is at different pauses.Fig.10 shows the acceleration data for the calibration phase.The acceleration sensing unit rotates around the X, Y, and Z axes, and pauses for ＞1 second when the x-axis sensing unit is in different quadrants of space.When the sensing unit is paused at a certain position, the first 8 acceleration vectors are obtained.The acceleration vector from the calibration phase is considered to have good quality because there is a large gap between them under spatial and static conditions (minimizing the effect of the acceleration motion of the sensing unit).The ninth acceleration vector moves from the first acceleration reading in the above figure to the last acceleration reading.Combine all 9 acceleration vectors to calculate the gain.

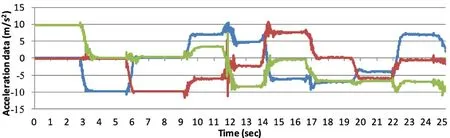
Figure 10: The acceleration data for the calibration phase

Figure 11: Sum of errors (εsum) when different ninth acceleration vectors

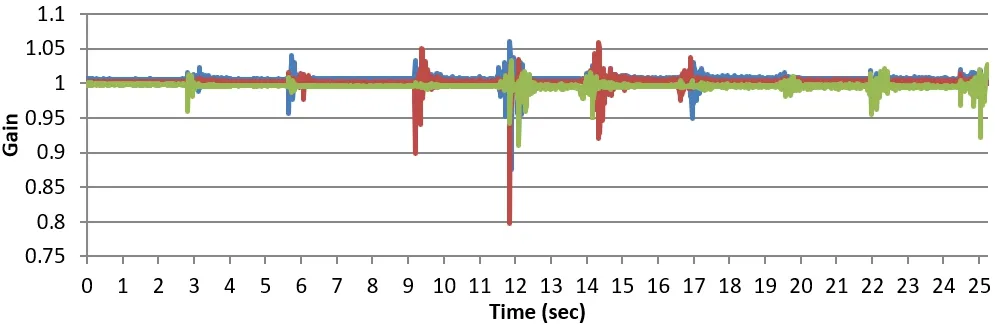
Figure 12: Calculate the auto-calibration gain for each group

Fig.13 shows When the different ninth acceleration vector is selected, the automatic calibration gain is calculated after the bad acceleration vector is removed.(bad acceleration vector is when sum of errors greater than 9.08, this is a calculated sum of error when all nine g vectors are obtained when Acceleration sensing unit pause at different position)

Figure 13: Sum of errors (εsum) when different ninth acceleration vectors

It can be seen from Fig.13 that the calculated auto-calibration gains are very close to 1, indicating that the accelerometer unit is well calibrated.As can be seen from the comparison Tab.3, the error after calibration is significantly less than before calibration.

Table 3: Gain and standard deviation comparison

Next, we collect another data set that rotates the sensing unit around the X, Y, and Z axes, and pauses for ＞1 second when the x-axis sensing unit is in different quadrants (approximately the first 20 seconds) in the space of the calibration phase.When the sensing unit is paused at a certain position, the first 8 acceleration vectors are obtained.The ninth acceleration moves from the acceleration reading at approximately 21 seconds in Fig.14 to the last acceleration reading.

Figure 14: The acceleration data for the calibration phase

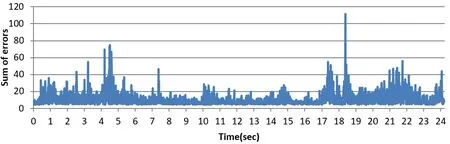
Figure 15: Sum of errors (εsum) when different ninth acceleration vectors

Figure 16: Calculate the auto-calibration gain for each group

Finally, we subtract the bad acceleration vector with different error (15 and 9.08) thresholds and then calculate the auto-calibration gain, see Figs.17 and 18.

Figure 17: The auto-calibration gain calculated after removal of the bad acceleration vector (when sum of errors greater than 15) when different ninth acceleration vectors obtained

Figure 18: The auto-calibration gain calculated after removal of the bad acceleration vector (when sum of errors greater than 9.08) when different ninth acceleration vectors obtained

Table 4: Gain and standard deviation comparison

5 Conclusion

Stroke survivors may lose control of upper limbs.FES therapy is a post-stroke rehabilitation intervention, and FSM has proven to be an effective and intuitive FES control method.The FSM uses the data information generated by the accelerometer to robustly trigger state transitions.In the medical field, highly accurate acceleration data is required, and the correlation of human motion analysis results directly depends on the accuracy of the collected data.Therefore, we need to calibrate the accelerometer.This paper proposes a method to calculate the auto-calibration gain robustly using redundant acceleration vectors.The least squares error model is used to calculate the error of the auto-calibration gain of each accelerometer’s sensitive axis.This method removes the limitations of calibration equipment and is superior to traditional laboratory calibration methods.In the experiment, we found that the error of partial calculation increases due to the existence of poor acceleration vector.For this reason, we have established a rule to eliminate the bad acceleration vector and calculate the automatic calibration gain.It has been experimentally shown that this may cause some error when the selected acceleration vector is not significantly separated.Therefore, we propose that in the automatic calibration method, when the acceleration sensing unit rotates, all acquired acceleration vectors should be separated from each other in space.Next, after the calibration phase, we move the acceleration sensing unit around the X, Y and Z axes and pause for ＞1 second when the x axis is in different quadrants of space, and obtain the first 8 acceleration vectors, which minimizes the acceleration of the sensing unit.The impact, then calculate the gain and compare.Experiments show that the calculated auto-calibration gain is very close to 1, which indicates that the accelerometer unit is well calibrated.It can be seen from the experimental comparison table that the error after calibration is significantly less than before calibration.

Acknowledgement:This work has received funding from the European Union Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no.701697, Major Program of the National Social Science Fund of China (Grant No.17ZDA092), Basic Research Programs (Natural Science Foundation) of Jiangsu Province (BK20180794), 333 High-Level Talent Cultivation Project of Jiangsu Province (BRA2018332) and the PAPD fund.

References

Burgar, C.G.; Lum, P.S.; Shor, P.C.; Hf, M.V.D.L.(2000): Development of robots for rehabilitation therapy: the Palo Alto VA/Stanford experience.Journal of Rehabilitation Research & Development, vol.37, no.6, pp.663.

Baidu Documents(2018): https://wenku.baidu.com/view/eff5868dbe1e650e53ea99c0.html.

Cai, Q.; Song, N.; Yang, G.; Liu, Y.(2013): Accelerometer calibration with nonlinear scale factor based on multi-position observation.Measurement Science & Technology, vol.24, no.10, 105002.

Ferrarin, M.; Palazzo, F.; Riener, R.; Quintern, J.(2001): Model-based control of FESinduced single joint movements.Neural Systems and Rehabilitation Engineering, vol.9, no.3, pp.245-257.

Fu, Q.; Chen, W.; Yu, J.; Zeng, Y.; Cao, X.(2010): The effects of motor imagery therapy on the upper limb motor function in hemiplegic stroke patients.Chinese Journal of Rehabilitation Medicine, vol.25, no.1, pp.53-55.

Fang, S.; Cai, Z.; Sun, W.; Liu, A.; Liu, F.et al.(2018): Feature selection method based on class discriminative degree for intelligent medical diagnosis.Computers, Materials & Continua, vol.55, no.3, pp.419-443.

Godfrey, A.; Conway, R.; Meagher, D.; OLaighin, G.(2008): Direct measurement of human movement by accelerometry.Medical Engineering & Physics, vol.30, no.10, pp.1364-1386.

He, W.; Wang, K.(2014): Advance in rehabilitation of upper limb function in hemiplegic patients after stroke (review).Chinese Journal of Rehabilitation Theory & Practice, vol.20, no.4, pp.334-339.

He, Y.; Hua, H.; Luo, H.; Liu, H.(2017): Effect of electromyographic biofeedback therapy on upper limb dyskinesia of stroke hemiplegic patients.China & Foreign Medical Treatment, vol.36, no.36, pp.93-95.

Ietswaart, M.; Johnston, M.; Dijkerman, H.C.; Joice, S.(2011): Mental practice with motor imagery in stroke recovery: randomized controlled trial of efficacy.Brain A Journal of Neurology, vol.134, no.5, pp.1373-138.

Jafari, M.; Sahebjameyan, M.; Moshiri, B.; Najafabadi, T.A.(2015): Skew redundant mems imu calibration using a kalman filter.Measurement Science and Technology, vol.26, no.10, 105002.

Jiang, X.Z.; Xiong, C.H.; Sun, R.L.; Xiong, Y.L.(2011): Characteristics of the robotic joint of a 9-dof upper limb rehabilitation robot driven by pneumatic muscles.International Journal of Humanoid Robotics, vol.8, no.4, pp.743-760.

Kwakkel, G.; Kollen, B.J.; Krebs, H.I.(2008): Effects of robot-assisted therapy on upper limb recovery after stroke: a systematic review.Neurorehabilitation & Neural Repair, vol.22, no.2, pp.111.

Lin, Z.; Chen, L.(2010).Effectiveness of functional electrical stimulation on functional recovery of the affected upper extremities in subjects with stroke: a randomized controlled trial.Chinese Journal of Rehabilitation Medicine, vol.25, no.2, pp.152-155.

Liu, Y.; Li, B.; Di, K.; Yang, L.; Fan, S.(2018): Optimization of nine-position calibration algorithm based on MEMS accelerometer.Piezoelectrics & Acoustooptics, vol.40, no.5, pp.780-783.

Liu, B.; Fang, J.(2008): Modified hybrid calibration method for IMU without orientation.Chinese Journal of Scientific Instrument, vol.29, no.6, pp.1250-1254.

Lum, P.S.; Burgar, C.G.; Shor, P.C.(2003): Use of the MIME robotic system to retrain multijoint reaching in post-stroke hemiparesis: why some movement patterns work better than others.International Conference of the IEEE Engineering in Medicine & Biology Society, vol.2 pp.1475-1478.

Lötters, J.C.; Schipper, J.; Veltink, P.H.; Olthuis, W.; Bergveld, P.(1998): Procedure for in-use calibration of triaxial accelerometers in medical applications.Journal of Applied Behavior Analysis, vol.68, no.1-3, pp.221-228.

Nez, A.; Fradet, L.; Laguillaumie, P.; Monnet, T.; Lacouture, P.(2016): Comparison of calibration methods for accelerometers used in human motion analysis.Medical Engineering & Physics, vol.38, no.11, pp.1289-1299.

Popovic, D.B.; Popovic, M.B.; Sinkjaer, T.; Stefanovic, A.; Schwirtlich, L.(2004): Therapy of paretic arm in hemiplegic subjects augmented with a neural prosthesis: a crossover study.Canadian Journal of Physiology and Pharmacology, vol.82, no.8-9, pp.749-756.

Syed, Z.F.; Aggarwal, P.; Goodall, C.; Niu, X.; El-Sheimy, N.(2007): A new multiposition calibration method for mems inertial navigation systems.Measurement Science and Technology, vol.18, no.7, pp.1897-1907.

Taub, E.; Uswatte, G.; King, D.K.; Morris, D.; Chatterjee, A.(2006): A placebocontrolled trial of constraint-induced movement therapy for upper extremity after stroke.Stroke, vol.37, pp.4, pp.1045-1049.

Taub, E.; Crago, J.E.; Uswatte, G.(1998): Constraint-induced movement therapy: a new approach to treatment in physical rehabilitation.Rehabilitation Psychology, vol.43, no.2, pp.152-170.

Titterton, D.H.; Weston, J.L.(2004): Strapdown Inertial Navigation Technology.The Institution of Electrical Engineers, USA.

Tresadern, P.A.; Thies, S.B.; Kenney, L.P.J.; Howard, D.; Goulermas, J.Y.(2008): Rapid prototyping for functional electrical stimulation control.IEEE Pervasive Computing, vol.7, no.2, pp.62-69.

Zhang, H.; Ye, X.(2009): A modified calibration model of IMU accelerator and rapid calibration method.Metrology & Measurement Technology, vol.29, no.3, pp.11-13.