Topological Characterization of Book Graph and Stacked Book Graph
2019-07-18RaghisaKhalidNazeranIdreesandMuhammadJawwadSaif
Raghisa Khalid, Nazeran Idrees, and Muhammad Jawwad Saif
Abstract: Degree based topological indices are being widely used in computer-aided modeling, structural activity relations, and drug designing to predict the underlying topological properties of networks and graphs.In this work, we compute the certain important degree based topological indices like Randic index, sum connectivity index, ABC index, ABC4 index, GA index and GA5 index of Book graph Bn and Stacked book graph Bm ,n.The results are analyzed by using edge partition, and the general formulas are derived for the above-mentioned families of graphs.
Keywords: Topological indices, Book graph Bn , Stacked book graph Bm ,n, network.
1 Introduction
Graph theory is used as a tool for designing and modeling chemical structures, complex network, and modeling of daily-life problems.In recent years, chemical structures and pharmaceutical techniques have been rapidly developed.In this period of rapid technological development, a huge number of new crystalline materials, nanomaterial, and drugs are designed using computer-aided modeling techniques.Researchers have found the topological index to be an influential and valuable tool in the narrative of molecular or network structure.A non-empirical scientific amount which quantitates the molecular structure and its branching pattern is described as a topological index of the associated graph.The chemical graph theory put on the tools from graph theory to mathematical models of molecular singularities, which is helpful for the study of molecular modeling and molecular structure.This theory plays a vigorous role in the field of theoretical chemical sciences.
In this paper all molecular graphs are considered to be connected, finite, loopless and deprived of parallel edges.Let F be a graph with n vertices and m edges.The degree of a vertex is the number of vertices adjacent to q and is signified as d(q) .By these terminologies, certain topological indices are well-defined in the following way.
The Randic index is the oldest degree based topological index and is signified as χ(F) and presented by Randic [Randic (1975)].He proposed this index for calculating the degree of branching of the carbon-atom skeleton of saturated hydrocarbons.Li et al.[Li and Shi (2008)] gave a comprehensive survey of the Randic index.
Definition 1.1For any molecular graph F, the Randic index is defined as

A variation of Randic connectivity index is the sum connectivity index [Zhou and Trinajstic (2009)].
Definition 1.2.For a molecular graph F, the sum connectivity index is defined as

Estrada et al.[Estrada, Torres and Rodriguez (1998)] proposed a degree based topological index of graphs, which is said to be the atom-bond connectivity index.Further, he proposed the atom-bond connectivity index of branched alkanes [Estrada (2008)].For the atom-bond connectivity index several upper bounds for graphs are established and also studied in the context of the connected graph, and bicyclic chemical graphs [Chen, Liu and Guo (2012); Chen and Guo (2012); Xing, Zhou and Dong (2011)].
Definition 1.3.Let F be a molecular graph; then ABC index is defined as

The geometric-arithmetic index is associated with a variation of physiochemical properties.It can be used as a possible tool for QSPR/QSAR research.Vukicevic et al.[Vukicevic and Furtula (2009)] introduced the geometric-arithmetic( GA) index.
Definition 1.4.Let F be a molecular graph, then geometric-arithmetic index is defined as

Ghorbani et al.[Ghorbani and Hosseinzadeh (2010)] presented the fourth ABC index.
Definition 1.5.Let F be a molecular graph; then ABC4index is defined as

where Sqis the summation of degrees of all the neighbors of a vertex q in F.
Recently Graovac et al.[Graovac, Ghorbani and Hosseinzadeh (2011)] proposed the fifth GA index, which is defined below.
Definition 6.Let F be a molecular graph; then5GA index is defined as

Degree based topological indices are rigorously studied for nanotubes, computer networks and many other chemical graphs, for recent development in literature [Idrees, Said, Rauf et al.(2017); Gao, Wu, Siddiqui et al.(2018); Idrees, Hussain and Sadiq (2018); Imran, Baig Rehman et al.(2018); Joan (2019)].Some other interesting results about network analysis using topological indices can be found in Hayat et al.[Hayat and Imran (2014); Javaid and Cao (2018)].
2 Main results for Book graph
Book graph Bnis obtained by taking cartesian product of star graph Sn+1with a path of length two P2, i.e.,Bn:= Sn+1□P2, as shown in Fig.1.The degree based topological indices like Randic index, sum connectivity index, atom-bond connectivity index, geometric-arithmetic index, fourth atom-bond connectivity index, GA5index for Book graph Bnare computed in this section.

Figure 1: A representation of Book graph nB

Table 1: Partition of edge created by the sum of adjacent vertices of every line
Theorem 2.1
Let Bnbe the book graph.Then
i) The Randic index of Book graph is
ii) The Sum-connectivity index of Book graph (Bn)is
iii) The Atom bond connectivity index of Book graph is
iv) The geometric-arithmetic index (GA) of Book graph is

Proof.For the Book graph Bn, we divider the edges of Bninto edges of the form Edq,dr, where qr is an edge.We develop the edges of the form E(2,2), E(2,n+1)andIn Fig.1, E(2,2), E(2,n+1)andare colored in red, lavender and green, respectively.The number of edges of these forms are given in the Tab.1.


Using Tab.1, we get

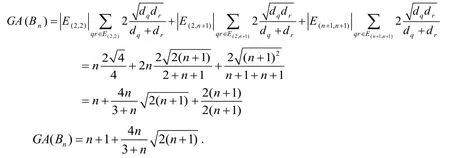
Theorem 2.2
i) The fourth atom bond connectivity index (ABC4) Book graph is
ii) The Fifth geometric arithmetic index (5GA)of Book graph is
Proof.Consider the Book graph Bn.The edges of Bncan be divided into edges of formwhere qr is an edge.We develop the edges of the formandthat are shown in Tab.2 given below, by evaluating sum of degrees of neighboring vertices.

Table 2: Partition of edges created by the sum of degrees of neighbors of the head-to-head vertices of every edge

From Tab.2, we get

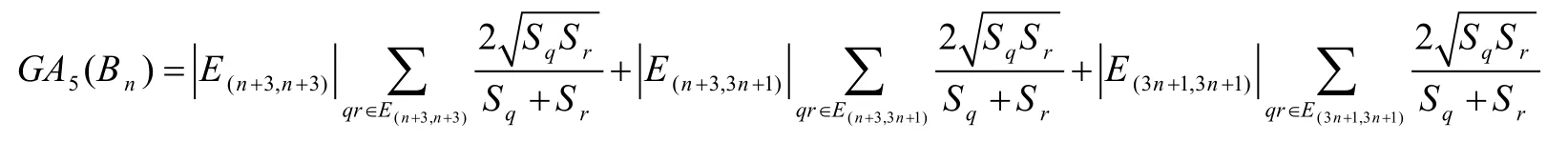
Substituting the values from Tab.2,
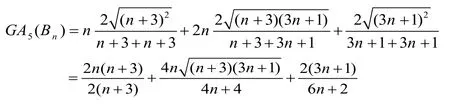
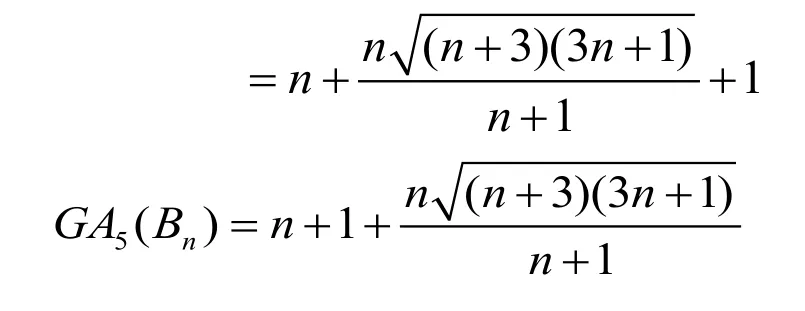
and we get the desired result.
3 Main results for Stacked book graph
The Stacked book graph of order (m,n), denoted by Bm,nis the Cartesian productof graphs, where Smis a star graph and Pnis the path graph on n points.It is therefore the graph resultant to the edges of n copies of an m-page book stacked one on top of another and is a generalization of the book graph.The degree based topological indices like Randic, sum, atom-bond, geometric-arithmetic, fourth atom-bond, fifth geometric-arithmetic connectivity index for Stacked book graph,mnB are computed in this section.These graph invariants are computed by edge partition based on degrees of end vertices of edges as given in Tab.3 below.
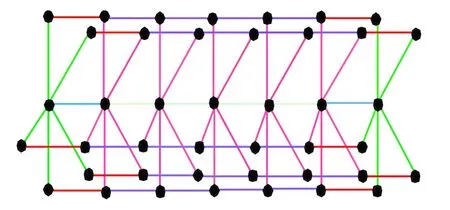
Figure 2: A representation of Stacked book graph B5,7

Table 3: Edge partition created by sum of adjacent vertices of every line
Theorem 3.1
i) The Randic connectivity index of Stacked book graph is
χ(Bm,n)=where 6n ≥ .
ii) The sum connectivity index of Stacked book graph iswhere n ≥ 6.
iii) The Atom bond connectivity index (ABC)of Stacked book graph is
iv) The Geometric-Arithmetic index (GA)o stacked book graph is GA( Bm,n)=Proof.Consider the Stacked book graph Bm,n.The edges of Bm,ncan be partitioned into edges of the form Edq,dr, where qr is an edge.In Bm,n, We develop the edges of the formandIn Fig.2,andare colored by red, bright green, lavender, pink, navy blue, and silver.The sum of edges of these forms is given in the Tab.3.

Substituting the values from Tab.3, we get,


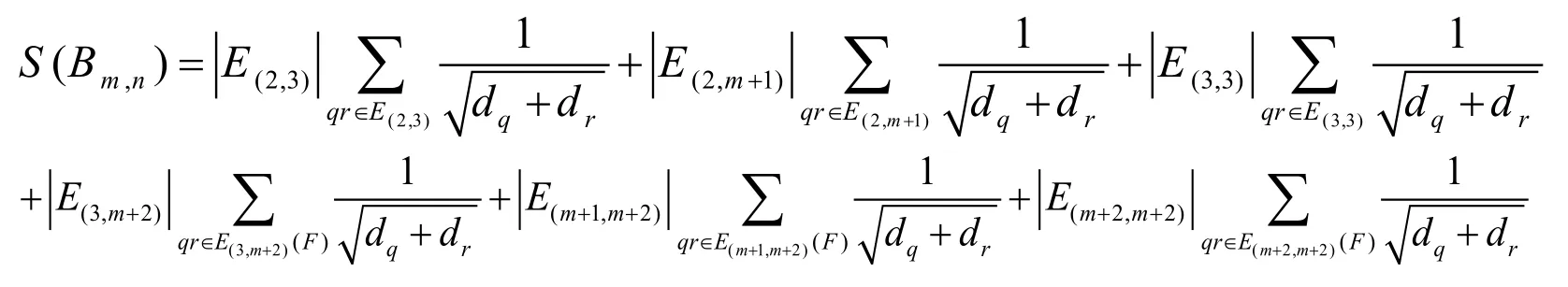
Substituting the values from Tab.3, we get


From Tab.3, we get,

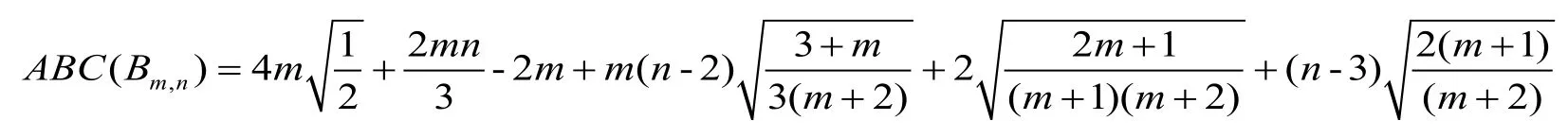
Using edge partition given in Tab.3, we have
After simplification, we have
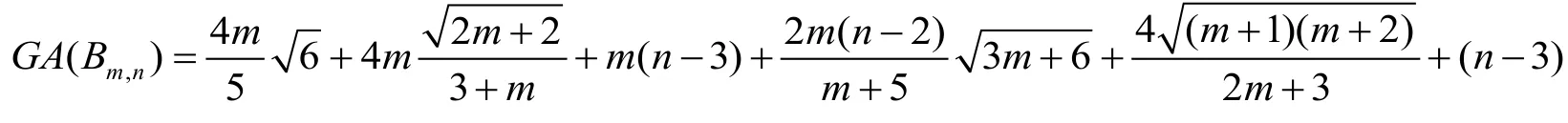
Theorem 3.2
The Fourth atom bond connectivity index (ABC4) and fifth geometric-arithmetic index (GA5) of Stacked book graph Bm,nare given as
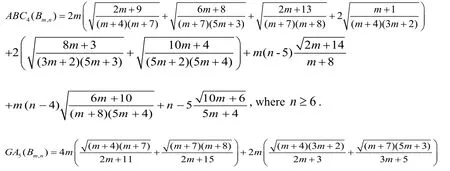

Proof.Consider the Stacked book graph,mnB .The edges of,mnB can be partitioned into edges of the formwhere qr is an edge.In Bm,n.We develop the edges of the formandthat are shown in Tab.4.

Table 4: Edge partition created by the sum of degrees of neighbors of the head-to-head vertices of every edge
Using the edge partition given in Tab.4, we have


After further simplification, we get

which yields the required result.

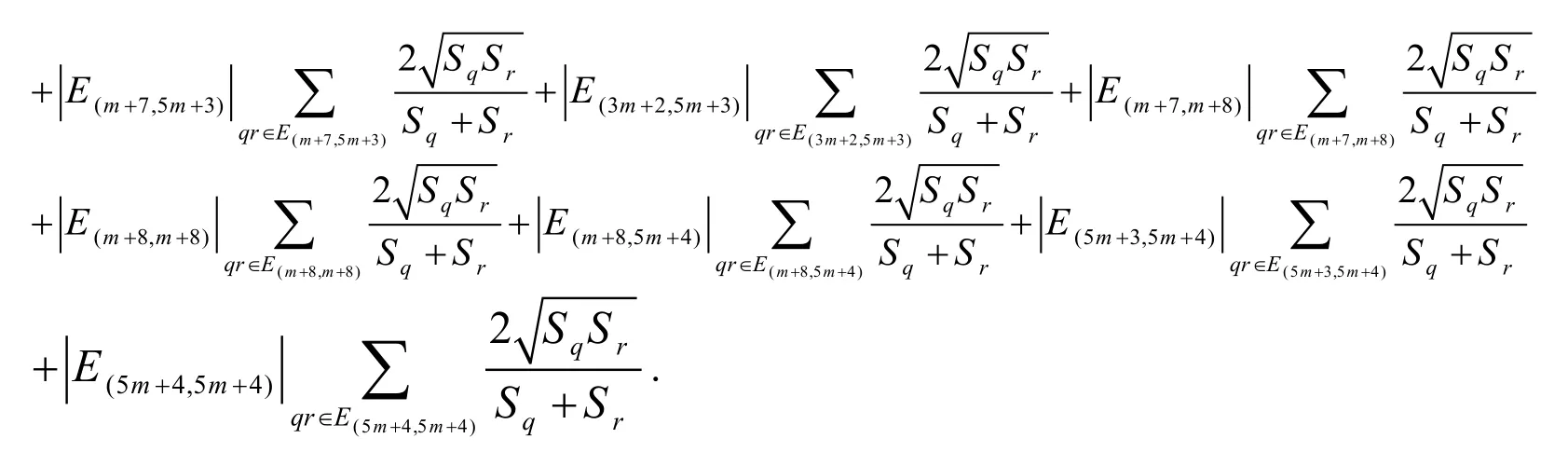
Again substituting the values from Tab.4, we get

4 Conclusion
In this work, we analyzed the graph-theoretic invariants of certain networks dependent upon connectivity of the nodes like ABC index, ABC4index, Randic connectivity index, sum connectivity index, GA index and5GA index of Book graphnB and Stacked book graph Bm,n.The results can be applied to investigate the topological properties of the computer network and structure-activity relation where the graph correspond to book graph and stacked book graph.We derived the general formulas of various degree based topological indices and computed the results analytically for the above-mentioned families of the graph.These graph-theoretic invariants depend upon connectivity of the nodes of the graph.These results can be employed to further understand the topological properties of graphs with graph-theoretic properties.
References
Chen, J.; Li, S.(2011): On the sum-connectivity index of unicyclic graphs with k pendent vertices.Mathematical Communications, vol.16, no.2, pp.359-368.
Chen, J.; Liu, J.; Guo, X.(2012): Some upper bounds for the atom-bond connectivity index of graphs.Applied Mathematics Letters, vol.25.no.7, pp.1077-1081.
Chen, J.S.; Guo, X.F.(2012): The atom-bond connectivity index of chemical bicyclic graphs.Applied Mathematics-A Journal of Chinese Universities, vol.27, no.2, pp.243-252.
Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I.(1998): An atom-bond connectivity index: modelling the enthalpy of formation of alkanes.Indian Journal of Chemistry, vol.37, no.10, pp.849-855.
Estrada, E.(2008): Atom-bond connectivity and the energetic of branched alkanes.Chemical Physics Letters, vol.463, no.4, pp.422-425.
Farahani, M.R.(2013): On the fourth atom-bond connectivity index of Armchair Polyhex Nanotubes.Proceedings of Romanian Academy Series B, vol.15, no.1, pp.3-6.
Ghorbani, M.; Hosseinzadeh, M.A.(2010): Computing ABC4index of nanostar dendrimers.Optoelectronics and Advanced Materials Rapid Communications, vol.4, no.9, pp.1419-1422.
Graovac, A.; Ghorbani, M.; Hosseinzadeh, M.A.(2011): Computing fifth geometricarithmetic index for nanostar dendrimers.Journal of Mathematical Nanoscience, vol.1, no.1, pp.33-42.
Hayat, S.; Imran, M.(2014): Computation of topological indices of certain networks.Applied Mathematics and Computation, vol.240, pp.213-228.
Idrees, N.; Saif, M.; Rauf, A.; Mustafa, S.(2017): First and second Zagreb eccentricity indices of thorny graphs.Symmetry, vol.9, no.1, pp.7-16.
Idrees, N.; Hussain, F.; Sadiq, A.(2018): Topological properties of benzenoid graphs.University Politehnica of Bucharest Scientific Bulletin Series B-Chemistry and Materials Science, vol.80, no.1, pp.145-156.
Javaid, M.; Cao, J.(2018): Computing topological indices of probabilistic neural network.Neural Computing and Applications, vol.30, no.12, pp.3869-3876.
Joan, K.(2019): Some topological indices computing results of archimedean lattices l (4, 6, 12).Computers, Materials & Continua, vol.58, no.1, pp.121-133.
Li, X.; Shi, Y.(2008): A survey on the Randic index.MATCH Communications in Mathematical and Computational Chemistry, vol.59, no.1, pp.127-56.
Randic, M.(1975): Characterization of molecular branching.Journal of the American Chemical Society, vol.97, no.23, pp.6609-6615.
Xing, R.; Zhou, B.; Dong F.(2011): On atom-bond connectivity index of connected graphs.Discrete Applied Mathematics, vol.159, no.15, pp.1617-1630.
Zhou, B.; Trinajstić, N.(2009): On a novel connectivity index.Journal of Mathematical Chemistry, vol.46, no.4, pp.1252-1270.
杂志排行
Computers Materials&Continua的其它文章
- A DPN (Delegated Proof of Node) Mechanism for Secure Data Transmission in IoT Services
- A Hybrid Model for Anomalies Detection in AMI System Combining K-means Clustering and Deep Neural Network
- Efficient Analysis of Vertical Projection Histogram to Segment Arabic Handwritten Characters
- An Auto-Calibration Approach to Robust and Secure Usage of Accelerometers for Human Motion Analysis in FES Therapies
- Balanced Deep Supervised Hashing
- A Novel Reversible Data Hiding Scheme Based on Lesion Extraction and with Contrast Enhancement for Medical Images
