Outage Capacity Analysis for Cognitive Non-Orthogonal Multiple Access Downlink Transmissions Systems in the Presence of Channel Estimation Error

Yinghua Zhang , Yanfang Dong, Lei Wang Jian Liu , Yunfeng Peng and Jim Feng

Abstract: In this paper, we propose a downlink cognitive non-orthogonal multiple access (NOMA) network, where the secondary users (SUs) operate in underlay mode.In the network, secondary transmitter employs NOMA signaling for downlink transmission, and the primary user (PU) is interfered by the transmission from SU.The expressions for the outage probabilities are derived in closed-form for both primary and secondary users in the presence of channel estimation error.Numerical simulation results show that the channel estimation error and the inter-network interference cause degradation of the downlink outage performance.Also the power allocation and the location have a significant impact on the outage probability.The numerical experiments demonstrate that the analytic expressions of the outage probabilities match with the simulation results.

Keywords: Cognitive radio, NOMA, serial interference cancellation, channel estimation error, outage probability.

1 Introduction

Non-orthogonal multiple access (NOMA) is a newly proposed 5G multiplexing technology, which can meet the rapidly growing demand of mobile services.By actively introducing interference at the transmitting end and adopting interference cancellation technology at the receiving end, NOMA can obtain higher spectral efficiency and improve system throughput compared with the traditional orthogonal transmission technology [Al-Imari, Imran and Xiao (2017); Islam, Avazov, Dobre et al.(2017); Dai, Wang, Yuan et al.(2015); Timotheou and Krikidis (2015); Yang, Wang, Ng et al.(2017); Zeng, Yadav, Dobre et al.(2017)].This is in line with the explosive data growth and access demand in the coming 5G era.Thus NOMA has attracted the attention of researchers all over the world.Especially in the cellular network of the Internet of Things (IoT), NOMA provides the need for large-scale connection of IoT devices with low delay by accommodating multiple users in the same frequency spectrum [Liaqat, Noordin, Abdul Latef et al.(2018); Liu, Song and Gui (2018); Borkar and Pande (2016)].For example, in Ding et al.[Ding, Dai and Poor (2016)], the authors consider a novel precoding and power allocation strategy to realize the potential of NOMA in IoT.These proposed strategies can be applied to scenarios with two users or more.In order to take advantage of uplink NOMA technology in reducing the energy consumption of secondary users, an edge computing solution based on the NOMA technique is presented in Kiani et al.[Kiani and Ansari (2018)].In the paper, the author minimizes the energy consumption of secondary users by utilizing an NOMA-based optimization framework.In DOCOMO [DOCOMO (2014)], the author uses NOMA scheme to improve the spectral efficiency which is essential for the construction of Internet of Things (IoT).NOMA technology now has been adopted in the 3GPP long term evolution [3rd Generation Partnership Project (2015)].

Similarly, in order to make full use of radio resources, researchers introduce NOMA technology into cognitive radio network (CRN), which allows multiple secondary users to adopt overlapping transmission mode on the same frequency band of authorized users to realize multi-user spectrum sharing and further improve the system performance of CRN [Lv, Ma, Zeng et al.(2018); Lv, Chen, Ni et al.(2017); Chen, Wang and Jiao (2017)].In [Lv, Ni, Ding et al.(2017)], the authors introduce NOMA scheme into a cooperative spectrum-sharing networks and compare the advantages of NOMA scheme with orthogonal multiple access (OMA).In Lv et al.[Lv, Chen and Ni (2016)], the authors propose a cooperative transmission scheme based on CR-NOMA network to achieve the maximum diversity at SUs.In these papers, the study mainly focuses on the scheme of power allocation and user locations to improve system performance which assumes perfect CSI.

However, it is rather difficult to obtain perfect CSI of the system in the practical application scenario.The power consumption of the system would increase heavily in order to obtain perfect CSI [Gedik and Uysal (2009)], especially in large-scale wireless networks [Liu, Luo, Liu et al.(2018)].Under these practical constraints, we focus on the application of imperfect CSI, which is of great significance to reduce system complexity and power consumption.Recently, in Yang et al.[Yang, Ding, Fan et al.(2016)], the optimal power allocation strategy based on the channel estimation errors has been studied, and the outage probability has been calculated to evaluate the system performance.Also NOMA technology in a downlink scenario with channel estimation errors is studied and the performance is evaluated by outage probability.In Arzykulov et al.[Arzykulov, Tsiftsis, Nauryzbayev et al.(2018)], with the existence of channel estimation errors, a scheme of decode-and-forward cooperative underlay CR-NOMA is studied, and the expressions of outage probability are derived.The authors choose a set of power allocation factors based on different distances to ensure the fairness of secondary users.In Liu et al.[Liu, Song and Gui (2018)], the authors propose a basic framework to evaluate the security and reliability of cooperative NOMA in cognitive networks.Compared with the traditional schemes, the proposed scheme can effectively improve the system performance.The change of transmission distance is also taken into account because that the path loss has significant impact on the outage probability.Furthermore, in most of the CRN models, the interference from the primary network on SUs is generally ignored, which decreases the criterion of QoS and reduces the effectiveness of CRN systems.Based on the above problems, we analyze the outage performance of a cooperative underlay downlink CR-NOMA network in the presence of channel estimation error.The channel estimation error is regarded as interference in the systems.In CR-NOMA network, we take into account both the channel estimation error and the inter-network interference between the primary network (PN) and the secondary network (SN).Also, we make a comparison between imperfect CSI and perfect CSI in NOMA systems.The closed-form expressions of outage probabilities are derived for both primary and secondary users.Simulation results show that the channel estimation error and the internetwork interference cause degradation of the downlink outage performance.Furthermore, the transmit distance has a significant impact on the outage probability, since the path loss is a dominant factor in the CR-NOMA network, which has a significant impact on the outage probability.

The paper is organized as follows.Section II gives a brief view of the system and channel model.Section III derives outage probability expressions of the SUs and PU respectively.Section IV discusses numerical and Monte Carlo simulations results.Finally, Section V concludes the paper with a summary and some final remarks.

2 System model

Consider a downlink CR-NOMA system which consists of one primary transmitter (P), one secondary transmitter (S) and one primary destination (P0)as well as N secondary destinations Uk(k=1,2,..., N), as shown in Fig.1.

Figure 1: System model of the CR-NOMA network

In CR-NOMA network, we assume that each node with a single antenna operates in a half-duplex mode.Each channel keeps independently with each other, and complies with identically distributed.The total transmission power at secondary transmitter is limited by Ps.Similarly, define the transmit power of primary user as Pt.We assume that hpp0, hsukand hsp0denote the channel coefficients from P to P0(P → P0), from S to Uk(S → Uk), and from S to P0(S → P0).Respectively, each channel satisfies complex Gaussian distribution with zero-mean and variance 1.For example, the channel coefficient pertaining from S tois denoted by hsukandThe channel between the transmitting end i and the receiving end j is given by

whereijd denotes the distance between the user i and j, and α represents the path loss parameter.Similarly, it can be obtained that

2.1 NOMA transmission protocol

As is known, in practical scenarios the feedback delay errors always cause the channel estimation errors.So it is rather difficult to obtain perfect CSI of the wireless network.The channel coefficients can be given as [Ikki and Aissa (2012); Wang, Liu and Dong (2012); Ma and Jin (2007)]:

where Psdenotes the transmission power, anddenotes the power allocation factor, with

Thus, the received signals at P0and Ukare given respectively as

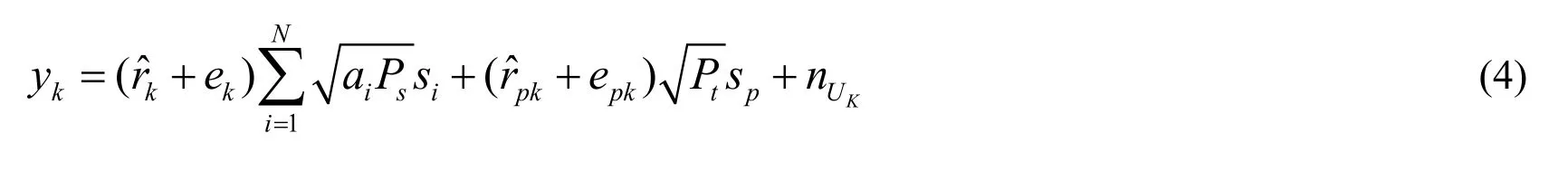
For the convenience of mathematical derivation, we assumeAnd denotesas the signal-to-noise ratio (SNR) of transmitting end.

During the secondary cooperative transmission process, it is assumed that the PU has a strong channel condition while the PU correctly transmits the message.Under such circumstances, we assume that the interference from the PU to the SU can be canceled at the secondary userTherefore, Serial interference cancellation (SIC) can be employed at Uk.Note that it is needed to detect the userwhose estimated gains of channel are worse than their own.If Ukdecodes the signal successfully, i.e.,wheredenotes the targeted rate of user Ui, then remove the signal si.Then Ukcan detect other userstep by step until Ukcan correctly decode its own signal.The general data rate expression for Ukto detect the signal is given by

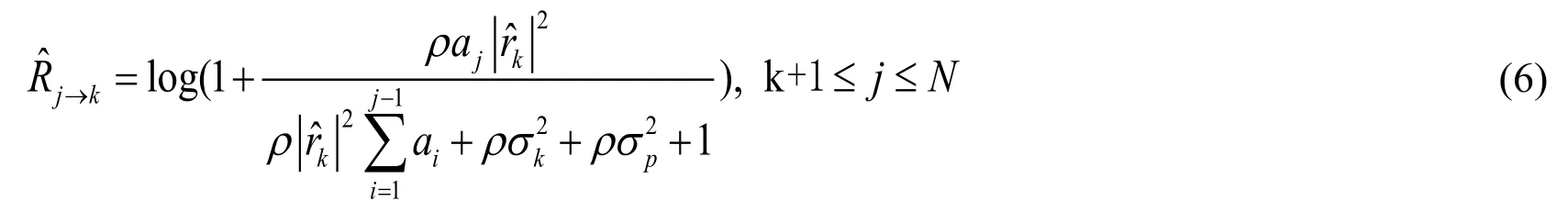
Now, if all the users Ui(k+ 1≤ i ≤N) correctly decode the message, the date rate of

user Ukcan be expressed as

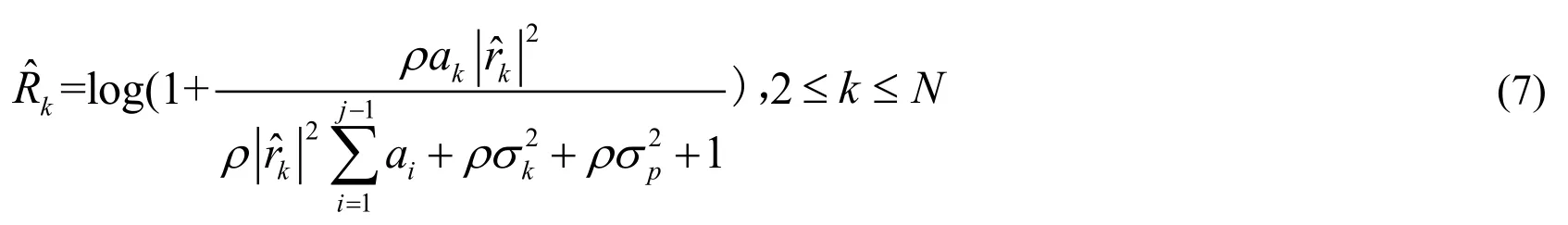
In particular, when k = j= 1,

In the downlink cognitive NOMA network, the user suffers interference from all of the other users.We assume that the estimated channel gain in the cell are sorted asis a strong channel user relative to all other users, so U1has interference-free transmission.

In underlay mode, the secondary users can establish cooperation transmission without exceeding the PU interference threshold.But the interference from the SU to the PU always exists.If the estimated error of the interference from the secondary users to the primary is ignored, the date rate of P0in the presence of channel estimation error is given by

Similarly, in practical systems, if the interference from SU to PU is within an controllable range, i.e.,and the channel estimation error of the interference is ignored, the date rate of0P in practical systems can be expressed as

2.2 Density functions of channel gains

According to statistics [David (2003)], in most cases the locations of users are fixed, and distances and path loss are deterministic.Also the fading is Rayleigh distributed.The cumulative distribution function (CDF) of the k-th estimation channel gainis given by Yang et al.[Yang, Ding, Fan et al.(2016)]

Therefore, the Probability density function (PDF) of the unordered channel gain is expressed as follows:

Given the fact that the interference imposed to the primary receiver is controllable, and the interference would not exceed the threshold of the PU, it is critical to ensure that the message of S be decoded at Uk, and the instantaneous receiving date rate of each useron the receiving end exceed the threshold of targeted rate set by each user in advance.andare the thresholds of date rate that can be properly demodulated by the PU and the i-th user respectively.Therefore, if the k-th user wants to achieve correct demodulation, it must satisfy these conditions:and

3 Performance of NOMA with channel estimation error

Suppose that the k-th user Ukcan successfully decodes its own signal and its subsequent signal as eventNote that the Ukneeds to detect its own signal, meanwhile the estimation channel of the gains of all of the other users are worse than its own.The event is expressed as

From Eq.(14), it can be seen that when the event can be established, it must satisfy:

During the secondary cooperative transmission process, the secondary users can establish cooperation transmission without exceeding the PU interference threshold.In other words, it refers to the secondary cooperative transmission while the primary user can transmit normally, i.e., γp＞γthp.Now, assume that the PU transmits normally, the outage probability is expressed as

From (18), the outage probability of is given by

Similarly, the outage probability of the PU is also worth our analysis.In this section, it can be clearly proved that the interference of secondary users to PU and the channel estimation error affect the outage performance.If SU transmits normally, the outage probability of user P0can be expressed as

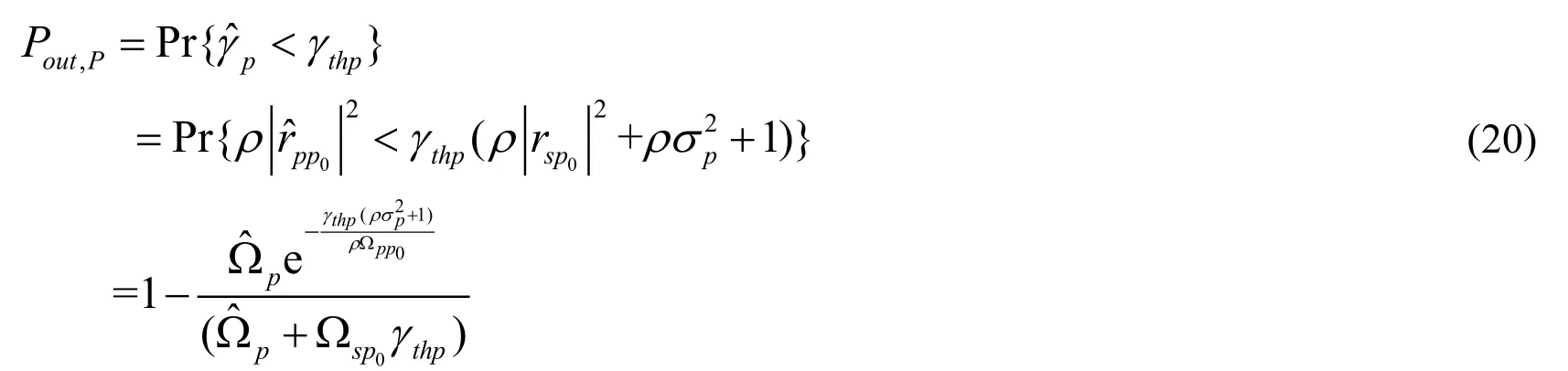
4 Numerical results and simulations

In this section, we set up a coordinate system firstly.Then simulations are performed here on the proposed scheme.Assuming that the CR-NOMA network has two secondary destination users (1U ,2U).So the distances between all of the users are expressed asand d2, respectively.The small-scale fading gain is Rayleigh distributed, i.e., hi～CN(0,1).The average channel coefficient is set aswith dkrepresenting the normalized distance between node S and node Uk.Assume that the path loss exponent α = 3, the power allocation factor a1=0.25, a2=0.75 and the distance dpp0=1m.Monte Carlo simulations are performed here to evaluate the performance of the proposed resource allocation algorithms.The simulation results are obtained after510 independent trials.

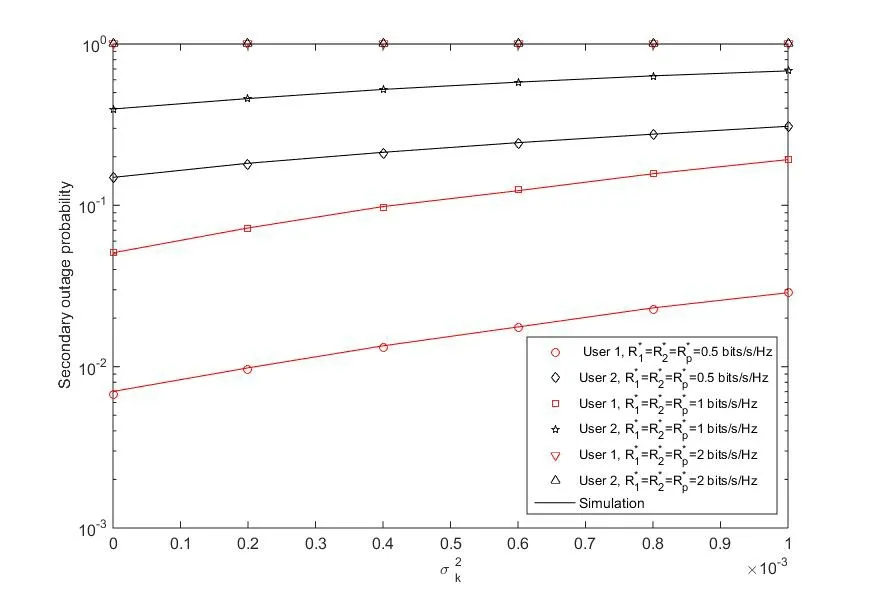
Figure 2: Impact of channel estimation error on secondary outage probability

Fig.2 shows the outage probability of SUs with channel estimation errors varianceobserved in NOMA.In the figure, the SNR is set as 30 dB, and the distances are set asWith the increase ofthe outage probability increases respectively.It can be seen that the simulation results match perfectly with the analytical results.Also larger channel estimation error brings stronger interference to the wireless system.In addition, it can be observed from Fig.2 that the outage probability will always be 1 when choosing larger value ofAt this point, the parameter selection scheme fails to satisfy the condition

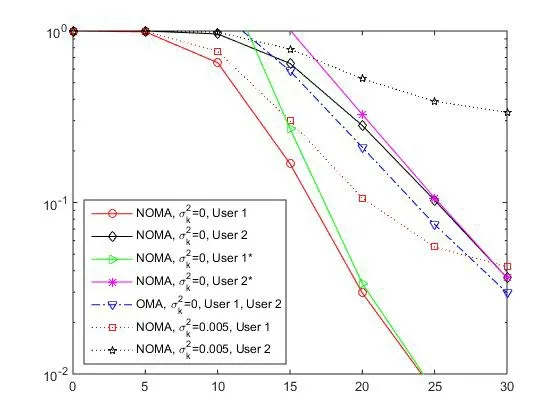
Figure 3: Impact of SNR on secondary outage probability.For the curve of User 1* and User 2* with under NOMA scheme, please refer to Yang et al.[Yang, Ding, Fan et al.(2016)]

Fig.3 depicts the impact of channel estimation erroron the outage probability of secondary user Uk.In the figure, we set the targeted ratebit/s/Hz , the distance d1= d2=5m and dsp0=10m.It is observed that the outage performance can be significantly improved by increasing the transmitting SNR.Numerical simulation results show that the channel estimation error caused by partial channel information has a significant impact on the outage probability of Uk.Furthermore, we compare the results of the NOMA atto those obtained from Yang et al.[Yang, Ding, Fan et al.(2016)].It can be observed from Fig.3 that the accurate results from Yang et al.[Yang, Ding, Fan et al.(2016)] can be achieved only with higher SNRs, and in the paper, the analytical results are in good consistence with Monte Carlo simulations within the overall range of SNR.Under NOMA scheme, the secondary transmission with imperfect CSI cannot obtain diversity gain due to channel estimation error, while secondary transmission with perfect CSI can obtain a diversity gain.

Fig.4 shows the analytical results of the primary outage probability.In the figure, the SNR is set as 30 dB, the distances d1= d2=5m and dsp0=10m.As can be seen from the figure, with the increase of error variance2pσ , the outage probability also increases, and the theoretical analysis results in Eq.(20) are in good consistence with Monte Carlo simulations.

Figure 4: Impact of channel estimation error on primary outage probability

Figure 5: Impact of SNR on primary outage probability

Fig.5 depicts the impact of channel estimation erroron the primary outage probability.In Fig.5, we set the targeted ratethe distancesThe outage performance of PU is compared both using imperfect CSI and perfect CSI in NOMA systems.As expected, NOMA scheme with perfect CSI outperforms scheme with imperfect CSI.Thus, the simulation here can verify the correctness of the conclusion on the above simulation of secondary transmission system.

Figure 6: Secondary outage probability vs.SNR with different transmission distance d2

From Fig.6, we can find the impact of SNR on the outage probability with different distance d2.We set the targeted rateand the distanceIt is observed from Fig.6 that, the lager we increase the transmitting SNR, the better outage performance can be got.Here we assume that the interference from the primary user to the secondary user is negligible.So the quality of data transmission only depends on the quality of the channel.From the Fig.6, with the increase of d2, the outage probability increases.This is because the increase of transmission distance d2leads to an increase of path loss and a deterioration of channel quality, which has a serious impact on outage performance.

Figure 7: Primary outage probability vs.SNR with different transmission distance d sp0of interference link

Fig.7 shows the outage probability simulation results of PU with different dsp0.The targeted rate is set asthe distanceAs can be seen from the figure, with the increase of SNR, the outage probability of the PU deteriorates.Also the outage performance decreases with the increase of dsp0.Concluded from the simulation, the performance of NOMA scheme with perfect CSI outperforms system with imperfect CSI.

5 Conclusions

In this paper, we propose a single-cell underlay downlink NOMA network.The interference of PN on SN is considered in the established model, and then we derive the expression of the outage probability for PU and SU.We also take channel estimation error into consideration and investigate the performance of NOMA scheme.Simulation results show that the outage performance deteriorates with the increase of the error variance and higher channel estimation error results in stronger interference.The Monte Carlo simulations match well with numerical results and NOMA scheme outperforms conventional OMA scheme.

Acknowledgement:This work is supported by National Major Project (No.2017ZX03001021005), NSFC Project (61871029) and 2018 Sugon New Model Program of Intelligent Factory on Advanced Computing Devices.

References

3rd Generation Partnership Project(2015): Study on Downlink Multiuser Superposition Transmission (MUST) for LTE (Release 13).3GPP Organizational Partners.

Al-Imari, M.; Imran, M.A.; Xiao, P.(2017): Radio resource allocation for multicarrier low-density-spreading multiple access.IEEE Transactions on Vehicular Technology, vol.66, no.3, pp.2382-2393.

Arzykulov, S.; Tsiftsis, T.A.; Nauryzbayev, G.; Abdallah, M.(2018): Outage performance of cooperative underlay CR-NOMA with imperfect CSI.IEEE Communications Letters, pp.1.

Borkar, S.; Pande, H.(2016): Application of 5g next generation network to internet of things.International Conference on Internet of Things and Applications, pp.443-447.

Chen, Y.; Wang, L.; Jiao, B.(2017): Cooperative multicast non-orthogonal multiple access in cognitive radio.IEEE International Conference on Communications, pp.1-6.

Dai, L.L.; Wang, B.C.; Yuan, Y.F.; Han, S.F.; I, C.I.et al.(2015): Non-orthogonal multiple access for 5g: solutions, challenges, opportunities, and future research trends.IEEE Communications Magazine, vol.53, no.9, pp.74-81.

David, H.A.(2003): Order Statistics, 3rd Edition.

Ding, Z.; Dai, L.; Poor, H.V.(2016): Mimo-noma design for small packet transmission in the internet of things.IEEE Access, vol.4, pp.1393-1405.

Ding, Z.; Yang, Z.; Fan, P.; Poor, H.V.(2014): On the performance of non-orthogonal multiple access in 5g systems with randomly deployed users.IEEE Signal Processing Letters, vol.21, no.12, pp.1501-1505.

DOCOMO(2014): 5G Radio Access: Requirements, Concepts and Technologies.NTT DOCOMO, Inc.

Gedik, B.; Uysal, M.(2009): Impact of imperfect channel estimation on the performance of amplify-and-forward relaying.IEEE Transactions on Wireless Communications, vol.8, no.3, pp.1468-1479.

Ikki, S.S.; Aissa, S.(2012): Two-way amplify-and-forward relaying with gaussian Imperfect channel estimations.IEEE Communications Letters, vol.16, no.7, pp.956-959.

Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K.(2017): Power-domain nonorthogonal multiple access (noma) in 5G systems: potentials and challenges.IEEE Communications Surveys Tutorials, vol.19, no.2, pp.721-742.

Kiani, A.; Ansari, N.(2018): Edge computing aware noma for 5g networks.IEEE Internet of Things Journal, vol.5, no.2, pp.1299-1306.

Liaqat, M.; Noordin, K.A.; Abdul Latef, T.; Dimyati, K.(2018): Power-domain non orthogonal multiple access (pd-noma) in cooperative networks: an overview.Wireless Networks, pp.1-23.

Liu, M.; Song, T.; Gui, G.(2018): Deep cognitive perspective: Resource allocation for noma based heterogeneous iot with imperfect sic.IEEE Internet of Things Journal, pp.1.

Liu, W.; Luo, X.; Liu, Y.; Liu, J.; Liu, M.et al.(2018): Localization algorithm of indoor wi-fi access points based on signal strength relative relationship and region division.Computers, Materials & Continua, vol.55, pp.71-93.

Lv, L.; Chen, J.; Ni, Q.(2016): Cooperative non-orthogonal multiple access in cognitive radio.IEEE Communications Letters, vol.20, no.10, pp.2059-2062.

Lv, L.; Chen, J.; Ni, Q.; Ding, Z.(2017): Design of cooperative non-orthogonal multicast cognitive multiple access for 5G systems user scheduling and performance analysis.IEEE Transactions on Communications, vol.65, no.6, pp.2641-2656.

Lv, L.; Ni, Q.; Ding, Z.; Chen, J.(2017): Application of non-orthogonal multiple access in cooperative spectrum-sharing networks over nakagami-m fading channels.IEEE Transactions on Vehicular Technology, vol.66, no.6, pp.5506-5511.

Lv, T.; Ma, Y.; Zeng, J.; Mathiopoulos, P.T.(2018): Millimeter-wave noma transmission in cellular m2m communications for internet of things.IEEE Internet of Things Journal, vol.5, no.3, pp.1989-2000.

Ma, Y.; Jin, J.(2007): Effect of channel estimation errors on m-qam with mrc and egc in nakagami fading channels.IEEE Transactions on Vehicular Technology, vol.56, no.3, pp.1239-1250.

Timotheou, S.; Krikidis, I.(2015): Fairness for non-orthogonal multiple access in 5G systems.IEEE Signal Processing Letters, vol.22, no.10, pp.1647-1651.

Wang, C.; Liu, T.C.; Dong, X.(2012): Impact of channel estimation error on the performance of amplify-and-forward two-way relaying.IEEE Transactions on Vehicular Technology, vol.61, no.3, pp.1197-1207.

Yang, Q.; Wang, H.; Ng, D.W.K.; Lee, M.H.(2017): Noma in downlink sdma with limited feedback: performance analysis and optimization.IEEE Journal on Selected Areas in Communications, vol.35, no.10, pp.2281-2294.

Yang, Z.; Ding, Z.; Fan, P.; Karagiannidis, G.K.(2016): On the performance of nonorthogonal multiple access systems with partial channel information.IEEE Transactions on Communications, vol.64, no.2, pp.654-667.

Zeng, M.; Yadav, A.; Dobre, O.A.; Tsiropoulos, G.I.; Poor, H.V.(2017): Capacity comparison between mimo-noma and mimo-oma with multiple users in a cluster.IEEE Journal on Selected Areas in Communications, vol.35, no.10, pp.2413-2424.