浅埋隧道穿越明城墙理论沉降变形值的研究

张世光

（中铁第一勘察设计院集团有限公司 陕西西安 710043）

1 工程背景

本次研究以山西某实际高速公路隧道下穿工程为依托，该隧道结构断面为扁平型拱形曲墙隧道，单洞双向通行，结构横向净空14.5 m、竖向限界高度5.0 m。根据隧道外部环境及地质条件，洞门形式为端墙式，洞门表面覆盖有装饰层。内部结构为复合衬砌支护结构；地层加固采用管棚＋超前锚杆＋超前小导管，进一步确保文物遗址的安全。土体地层参数见表1。

_表1_地层参数

2 理论分析

对于隧道穿越建构筑物这类问题，往往影响因素很多，针对地表沉降和建（构）筑变形、拱顶沉降、围岩压力、水平收敛等各项指标的分析及应用显得更为重要［1］。对于本次研究的对象明城墙来说，其材料以夯填土为主，在理论分析时应当以土力学中土体材料性质为出发点，通过分析土体在弹性阶段与弹塑性阶段的临近剪切屈服应力、粘聚力及内摩擦角等土体参数，最终确定控制标准的理论公式解［2］。为了满足工程的可实施性，该结论公式应当简洁且实用。

首先我们需要将实际问题转化为力学模型，本文决定采用弹性地基梁模型进行分析，其原因可解释为以下3条：（1）土体虽具有非均质性和非理想弹性，但土体实际上是一种具有弹塑性及粘滞性的介质，实际工程中土体所承受的应力较低，土体的应力应变在该情况下往往表现为线性关系［3］，因此，当土体间的性质相差不大时，采用弹性理论计算是允许的；（2）土体虽然不是连续介质，应力传递需要通过颗粒间的接触来完成，但由于一般建筑物的基础尺寸远远大于土粒尺寸，且在工程计算中，通常按照作用面上的平均应力来考虑，因此可以忽略土体的分散性［4］；（3）明城墙墙体为夯填土，土体致密，与地基土相比其弹性模量差异较大。

文克尔（winkler）提出在计算浅层弹性地基梁时，地基模型可以假定看做该点所承受的压力与该点处的竖向位移成正比：

齐梅尔曼（Zimmermann）优化提出地基模型可以假定看做该点接触应力值只与该点地基沉降量成正比：

式中，P（x，y）为单位面积上的压力强度；w（x，y）为地基的沉陷量；k、k0为地基反力系数。

该公式理论基础考虑了地基与土的约束作用，变形连续且协调，通过材料力学微分方程的解可知，当有q（x）荷载作用时，基础与弹性梁之间的位移y（x）与地基反力P（x）有以下关系：

式中，q（x）为作用在结构上的荷载；P（x）为地基与梁之间的压力；y（x）为梁与地基的共同位移；E为地基梁的弹性模量；I为惯性矩。

将（1）、（2）代入（3）并且令

式中，L为特征长度；β为特征系数。

该公式的齐次方程解通解可写为：

式中，A、B、C、D可由边界条件确定。

由于隧道开挖对于明城墙的影响范围是有限的，故地基梁未影响的两端可看做固定端，由于推导得出的沉降齐次方程A、B、C、D参数确定需要知道固定端的准确位置。而隧道施工时，工序与空间位置不断变化，参数不易确定［5］且公式只考虑了地基梁与地面共同作用影响而未考虑隧道施工影响，故不能直接运用。

为了解决这一问题，我们引入Peck沉降槽理论公式近似模拟地面沉降。

Peck认为隧道施工引起的地面横向沉降槽公式为：

式中，S（x）为与坐标原点（中轴线）相距x（m）处的地层沉降值；Smax为隧道曲线最大沉降量（m）；Vt为施工引起的地层损失（‰）；i为地表沉降槽宽度（m）［6］。

Peck公式虽然能够反映隧道施工对地面沉降的影响，但未考虑隧道上方有附加荷载或建构筑物的情况。对于本次研究的对象，明城墙主要材料为夯填土，弹性模量较大，假定弹性地基梁与地基连续接触，若将城墙高度按照隧道埋置深度考虑，这时Peck沉降槽公式可以近似等同于弹性地基梁沉降曲线公式。

材料力学中给出了梁结构变形与内力的关系式为：

由公式（9）可知，只要有明确的地基梁沉降公式就可以得到结构内力，进而建立起内力与沉降之间的关系。

综上所述，明确了采用的沉降公式（7）、（8）及内力表达式（9），接下来需要确定极限控制指标。对于一个结构而言，抗剪强度、抗拉强度及抗压强度等指标达到极限状态都会引起结构破坏。隧道穿越明城墙时，其破坏主要是因隧道施工造成的沉降过大引起的。沉降量最大处即为控制性截面［7］，由Peck公式可知，控制截面为洞顶处，即Peck公式中x＝0处，将沉降公式（7）代入公式（9）中求导得到控制截面（x＝0）受力公式为：

由公式（10）可知，x＝0截面上只有弯矩作用，故只需明确了极限内力σs对应的极限弯矩值M，即可得到极限沉降量Smax的理论推导值。

在确定极限弯矩值M时，我们引入土力学中摩尔库伦（Mohr-Coulumb）屈服准则［8］，具体摩尔库伦原理不再赘述，仅给出屈服主应力表示式为：

当规定σ1＞σ2＞σ3时，上式化简变为下式：

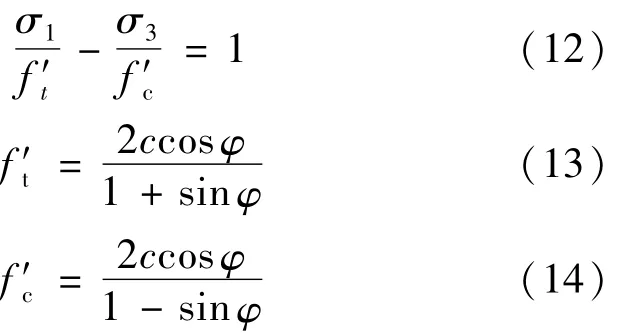
式中，f′t为土体达到Mohr-coulumb屈服准则时的单轴拉伸屈服应力；f′c为单轴压缩屈服应力［9］。

这里f′t和f′c即为所求的极限内力 σs。

由弹塑性理论知识得，当结构截面只受弯矩作用时，塑性变形范围会随着弯矩增加逐渐由边缘向内部发展，弹性区域与塑性区域共同存在，交接处正应力为屈服应力σs（见图1），应力沿高度分布为：

式中，ys为横截面到中性层的距离。

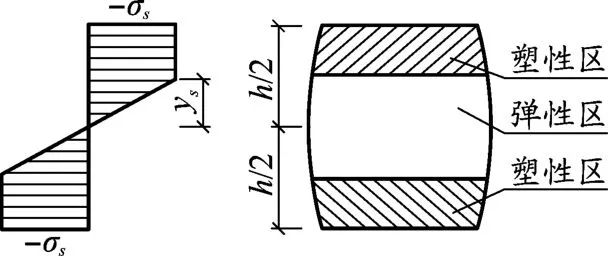
图1 应力分布

弹塑性理论知，受力满足：

式中，Ie为弹性区惯性矩；Sp为塑性区静矩；h为梁的横截面高；b为梁的横截面宽［10］。

当截面为矩形时，则有：

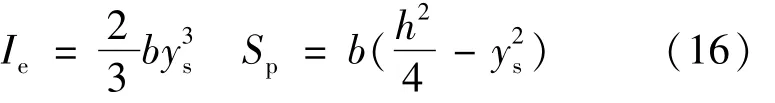
将公式（16）代入公式（15）得：

将ys＝0与ys＝h／2代入公式（17），可分别得到地基梁计算截面的弹性极限弯矩［M1］［11］（开始出现塑性变形），地基梁计算截面进入全塑性状态的塑性极限弯矩［M2］。

3 确定控制标准值

将公式（7）代入（9）中求导化简后可得沉降控制标准公式为：

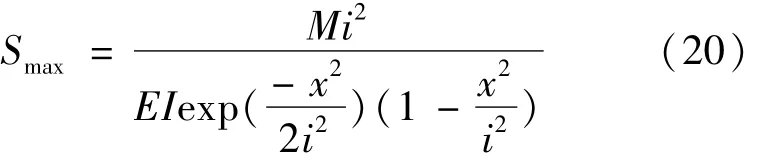
由结构力学知道两端固定的梁，弯矩最大处最先产生塑性区，且沉降量最大，为最危险截面（x＝0），Smax为：

将公式（18）代入（21），（18）公式中 σs按公式（13）计算，得到对应的拉应力弹性极限弯矩作用下的极限沉降量为：

将公式（18）代入（21），（18）公式中 σs按公式（14）计算，得到对应的压应力弹性极限弯矩作用下的极限沉降量为：

将公式（19）代入（21），公式中 σs按公式（14）计算时，得到对应的全截面塑性极限弯矩作用下的极限沉降量为：22

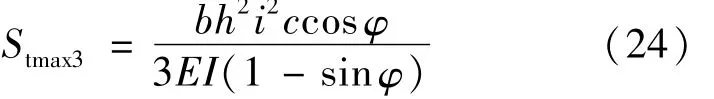
在此需注意，结构仅能在全截面受压情况下达到完全塑性破坏，故全截面塑性极限沉降量公式仅有一个［12］。计算所需的明城墙结构及地层参数见表2。

_表2_沉降公式参数

将表中参数代入推导公式（22）、（23）、（24）中得到沉降控制标准值的理论解：

开始产生拉应力塑性区的沉降量为：

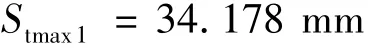
开始产生压应力塑性区的沉降量为：

全截面达到塑性区的极限沉降量为：

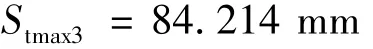
根据实际情况，明城墙破坏时不会处于全截面塑性破坏，因此将拉应力塑性极限沉降量，即34.178 mm作为沉降控制标准理论值。

4 结束语

本文将隧道下穿明城墙问题转化为弹性地基梁结构变形受力问题进行分析，分析过程中实际沉降曲线采用了Peck沉降槽经验公式进行模拟，对公式进行数学处理后，建立起了沉降与内力的关系，最终结合摩尔库伦屈服准则，并对弹塑性边值问题进行分析后给出了明城墙的极限沉降量控制标准值。通过对所穿越山西某隧道的实际监测，所得的理论沉降控制标准值保证了工程的顺利完成，作者希望通过本文的发表为相似穿越工程的理论分析提供参考思路。