某铁路站房大跨屋盖钢结构设计与分析

殷 静

（中铁第四勘察设计院集团有限公司 湖北武汉 430063）

1 引言

目前公共建筑为实现大跨空间，普遍采用下部混凝土结构与上部钢屋盖结构的组合形式，铁路旅客站房就属于这类典型的公共建筑。在对站房施工图进行审核的过程中发现很多设计院在设计时常常各自分开计算，即下部主体结构设计时，将上部钢屋盖等效成钢梁或楼板计算，并未真实考虑钢屋盖对下部结构的刚度贡献；进行上部钢屋盖设计时，常常也未考虑下部结构对上部屋盖的边界影响［1-2］。为此，本文选取铁路站房中比较常见的站型及规模，在施工图审核过程中通过单体钢屋盖模型和整体模型的对比，分析两种模型的受力特性，研究大跨钢屋盖与其下部混凝土结构的协同工作特性及抗震薄弱环节，从而验证结构体系选型的合理性及结构安全性，为今后类似工程施工图审核提供参考［3］。

2 工程概况

某铁路站房南候车厅建筑平面尺寸约为139 m×48 m，建筑高度约28.4 m。结构地上四层，一、二层层高为4.8 m；地下二层，地下一层为地铁集散厅，层高5 m，局部地下二层为地铁换乘层。下部结构柱网尺寸8.1 m、15.6 m和24 m，屋盖纵横向最大跨度36 m，建筑剖面图见图1。

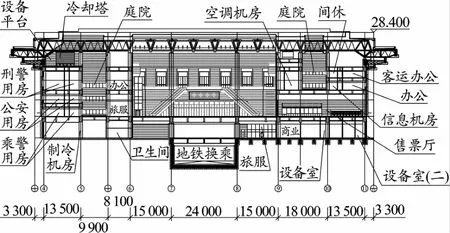
图1 铁路站房剖面（单位：mm）

该建筑设计使用年限为50年，安全等级为一级，结构重要性系数1.1。

2.1 设计荷载

（1）恒荷载

①结构自重:放大1.1倍考虑节点重量；②屋盖上弦荷载:金属屋面0.65 kN／m2；玻璃屋面1.0 kN／m2；③屋盖下弦荷载:吊顶及吊挂0.35 kN／m2，马道1.0 kN／m2；设备管道荷载根据实际布置按线荷载施加。

（2）活荷载 0.5 kN／m2；马道检修活荷载 1 kN作用在跨中验算。

（3）风荷载

根据《建筑结构荷载规范》（GB 50009-2012）［4］（下文简称荷载规范），基本风压按百年一遇取值为0.45 kN／m2，地面粗糙度类别为A类。

（4）雪荷载

基本雪压按照100年重现期取0.5 kN／m2，同时考虑雪荷载不均匀分布以及半跨均布的情况。

（5）温度荷载

根据当地气候特征资料，同时参考荷载规范［4］，控制钢结构合龙温度在10～15℃，取升温+30℃、降温-30℃进行温度工况的施加。

（6）地震作用

根据《建筑抗震设计规范》（GB 50011-2010）［5］，工程抗震设防烈度为7度（0.1 g），抗震设防类别为乙类；设计地震分组为第二组，场地类别为II类。

2.2 设计荷载组合

工程设计荷载组合见表1。表中各个荷载工况的分项系数和组合值系数按照荷载规范取值，由于该工程属于大跨度空间结构，因此适当考虑了竖向地震作用组合。

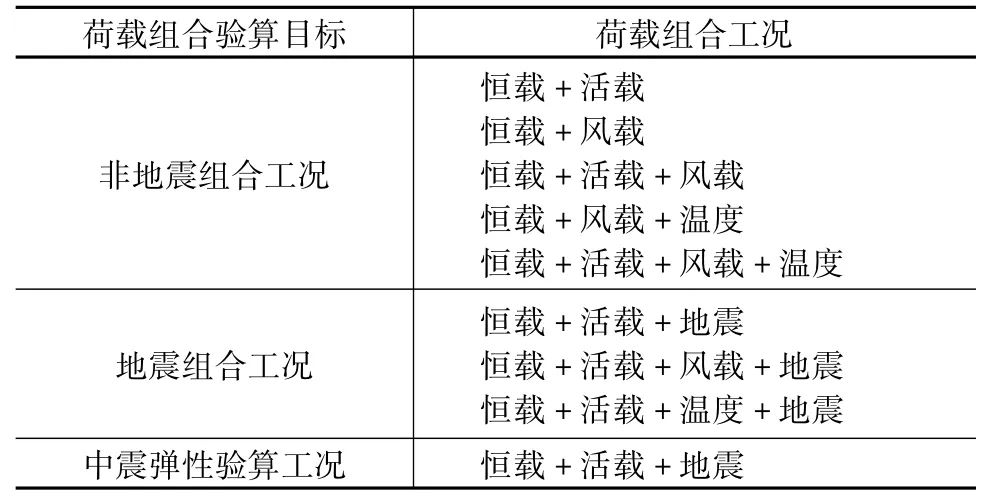
表1 荷载组合

3 屋盖结构体系

该铁路站房屋盖采用正交正放管桁架结构体系，根据建筑效果及支承条件，将桁架分为立体桁架和平面桁架两种［6］。其中，作为主受力桁架，立体桁架沿双向交错布置。悬挑部分采用平面桁架，共37榀，最大悬挑长度约14 m，平面悬挑桁架间通过支撑连接形成整体。屋盖立体桁架杆件及平面桁架腹杆采用无缝圆钢管，平面桁架弦杆采用矩形钢管，材质为Q345B。节点采用相贯节点和焊接球节点。图2为屋盖桁架轴测图。

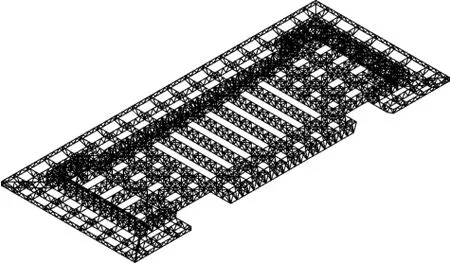
图2 屋盖桁架轴测图

立体桁架为倒三角形桁架，桁架下弦采用φ325×20，中间大厅由于建筑采光要求，采用单向立体三角桁架，桁架边部设置支撑和系杆，保证其空间稳定性。根据建筑造型的要求，高低变化处通过设置局部双层桁架来实现（见图3～图5）。

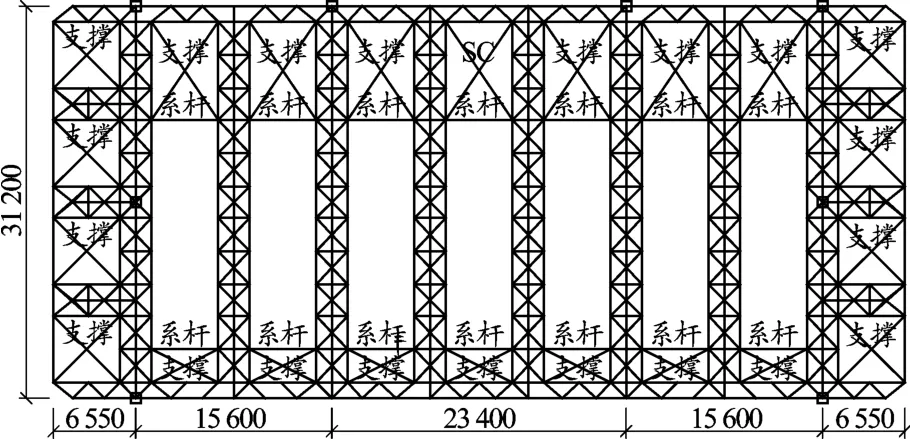
图3 中间采光大厅屋盖结构布置（单位：mm）

图4 局部双层桁架示意（单位：mm）

图5 立体、平面桁架转换示意

4 设计思路

4.1 上部钢屋盖结构设计

对于上部钢屋盖结构，设计过程中常用的边界约束条件有静定约束和全三向铰接两种。采用静定约束边界条件时结构跨中位移偏大，杆件内力小；而采用全三向铰接约束边界条件时结构跨度位移小，杆件内力大（尤其是支座附近）。

本工程采用静定约束和全三向铰接两种不同的边界条件进行包络设计，通过取两种模型的包络位移和内力，验算屋盖结构位移、杆件应力比等指标是否满足要求。

4.2 总装结构设计

通过建立下部结构的总装模型，对钢屋盖进行验算，对考虑下部结构实际刚度后的结构受力特性进行分析，并对屋盖结构杆件再次进行包络设计［7］。

采用Midas Gen软件分别建立钢屋盖单体模型和整体模型，其中单体模型为考虑不同边界约束包络设计后的静定约束模型。Midas Gen中桁架弦杆采用梁单元，桁架腹杆采用桁架单元。钢屋盖单体模型和整体模型见图6～图7。

图6 钢屋盖单体模型

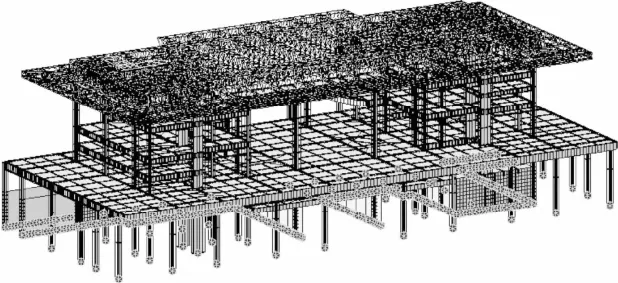
图7 总装模型

5 上部钢屋盖结构

5.1 单体钢结构屋盖结果分析

（1）挠度

1.0恒载+1.0活载下，桁架结构中心区域竖向挠度最大，最大挠度值为111 mm，挠跨比为1／324（跨度36 m）；周边悬挑端挠度值为33 mm，挠跨比为 1／333（悬挑 11 m），见图 8，均满足规范［8-9］规定的挠度限制要求。要求施工单位在施工过程中对挠度较大处采取适当的起拱措施。

（2）杆件应力比

①非地震组合和多遇地震组合工况验算

图8 标准组合下挠度值

非地震组合和多遇地震组合工况下，考虑压杆稳定系数，杆件应力比基本控制在0.85以下，个别杆件应力比达到0.9（支座处），满足设计控制指标。杆件验算应力比统计图及杆件应力比分布图见图9、图 10。

图9 杆件应力比统计

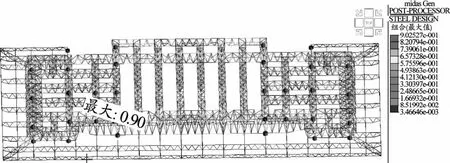
图10 杆件应力比分布图

②中震弹性验算

支座附近杆件为屋盖结构的关键构件，设计过程中对其采用中震弹性验算，并考虑压杆稳定系数。取消地震内力调整后，杆件应力比最大值为0.9，满足中震弹性的控制指标。

5.2 总装模型分析

（1）挠度及应力比

采用midas Gen对屋盖单体模型和总装模型进行对比分析，得到两种模型在同样荷载条件下的挠度值和杆件最大应力比，见表2。

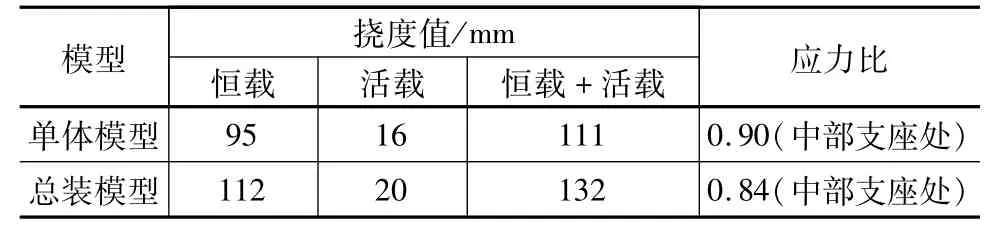
表2 两种模型结果对比

由表2可知，单体模型由于假定下部结构为无限刚体，采用三向铰接计算；而总装模型考虑了下部结构的实际刚度，因此单体模型的挠度值比总装模型小，但由于单体模型支座约束较强，应力比会比总装模型偏大。对于结构构件设计，采用两种边界约束条件包络设计后的单体模型是偏于安全的，与总装模型计算结果接近。

（2）周期

结构前三阶振型和周期见图11。第1阶振型为X向平动，周期为1.180 s；第2阶振型为Y向平动，周期为0.988 s；第3阶振型为扭转，周期为0.947 s。周期比为0.802，满足规范要求。

由图11可以看出两种模型屋盖部分振型形式基本一致，但整体模型中除竖向振型之外还夹杂较多的平动振型，这与下部混凝土部分参与振动有关。

图11 结构前三阶振型

（3）下部结构总装分析与单体分析对比

采用midas Gen进行分析后，提取总装模型和下部单体模型的结构关键参数结果进行对比，具体见表3。

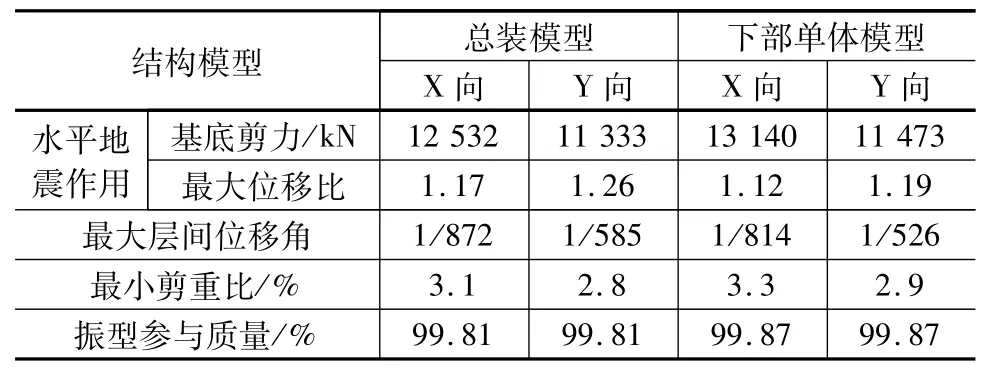
表3 关键参数结果对比

由表3可知，总装模型的基底剪力略小于单体模型，但相差不大；总装模型位移比偏大，这可能是由于上部钢屋盖鞭梢作用的原因［10］，对于与钢屋盖相连的混凝土框架柱的内力有放大作用，设计时应适当加大该框架柱配筋。

6 支座节点构造设计

支座节点不仅能阻止结构发生刚体位移，增强结构的整体性能，同时可有效抵消结构支座的部分反力［11-12］。该站房钢屋盖支座在设计时考虑如下因素:

（1）支座节点构造需满足计算假定；

（2）支座节点各部位尺寸应避免与其他构件碰撞，且保证足够净距以保证结构的控制变形；

（3）保证钢屋盖在地震作用下的安全性，尤其是支座处的安全可靠性。

本工程选用抗震球形支座，构造如图12所示。通过提取模型中的支座受力，确定支座产品参数。

图12 支座节点构造（单位：mm）

7 结论

（1）针对某铁路站房大跨度钢结构屋盖的设计思路和流程进行了详细介绍，根据建筑自身造型要求选用了合理的结构体系。

（2）单体钢屋盖结构应采用静定约束边界条件和全三向铰接边界条件进行包络设计。

（3）总装模型结果对比分析表明:采用两种边界约束条件包络设计后的单体模型进行设计偏于安全，与总装模型计算结果比较接近。

（4）对于下部混凝土结构，考虑上部钢屋盖的鞭梢作用后，与其相连的下部混凝土框架柱受力有所增加，该框架柱配筋建议适当放大。

（5）该铁路站房结构的控制指标严格按照相关规范制定，各项设计结果均满足规范要求，可为今后类似工程提供参考。