“微专题”课型在高考数学二轮复习中的实践与思考

2019-07-18广东省广东实验中学越秀学校510000唐郁文

中学数学研究(广东) 2019年12期

关键词：微专题题组棱柱

广东省广东实验中学越秀学校(510000)唐郁文

一、“微专题”课型复习的特点与优势

“微专题”课型是指运用微专题形式进行课堂授课的模式.微专题就是指从某一具体考点出发研究,将其所涉及的基本概念、基本定理、基本解题方法通过题组形式呈现,帮助学生内化知识,构建结构,再进行知识的迁移、整合和运用的教学设计.

1、微专题的特点

(1)微.所谓“微”,指专题的入口小、容量小、聚焦点小,一个微专题复习一般一至两节课即可.

(2)专.所谓“专”,指专题内容具有典型性、代表性和深度,能让学生学会一题通一类.

(3)准.所谓“准”,指专题能针对针对高考的常考点、热点问题,学生的易错点、易混点,让学生能精准进行备考复习,切实解决学生学习中真正需要解决的问题.

2、二轮复习运用“微专题”课型的优势

二轮复习的目标是让学生夯实基础,整合知识,构建体系,具有又快又准地找到解决具体题目的能力.高考中学生面对是一个个具体题目,它们的设问通常口径小,这与二轮大专题复习口径大不能与有效对接.“微专题”课型的特点,能较好的解决高考命题“基础性、综合性、应用性、创新性”的四翼要求,有效解决二轮大专题复习口径大的问题.精心挑选“微专题”课型内容,从高考必备的数学基本概念、基本定理、基本解题方法出发,设计好题组,把教学内容微专题化,“讲透”微专题,促进学生的知识体系、解题方法体系的建构,使学生掌握数学学科的基本理论和知识的内在逻辑,培养学生的理论思维和系统综合能力,提高学生知识和解题方法的应用能力,并到达思维和解题上的一些创造性和创新性的发展.

二、“微专题”课型在二轮复习中的实践

1、“微专题”课型内容的确定

在时间有限的二轮复习中,如何选择“微专题”课型的内容就特别重要了,笔者通过实践,提出可分三步走.

(1)运用“大数据”分析,初定专题方向.随着科技的发展和运用,大数据运用也进入了日常的教学,我们将高三的周测、月考、大考等数据都进行分析,找出学生阶段性的易错易混淆的知识点、题型在哪里,通过集体的备课的方式,结合学生的能力和高考定位,初选出微专题方向.

(2)根据高考命题要求,选定微专题内容.微专题的内容不宜太难,根据高考命题要求,选择学生易错的基本概念、基本定理、基本解题方法,通过基本能力的提升,打开一类题的解题之门,内化知识,构建解题体系.

(3)根据学生实际情况,精选例题.要让学生在高三的几轮复习中要都有持续地学习热情,就要让学生跳出“题海”,精讲精练;就要让学生在复习过程中有进步和成就感.所以教师要根据学生的实际的学情和考情,精心挑选吻合实际需要的“微专题”内容的例题,一般优选高考真题.

2、“微专题”课型的设计思路

著名心理学家和教育学家布卢姆说:“有效的教学始于准确地知道需要达到的目标是什么.”因此教学目标是课堂教学的灵魂.“微专题”设置的目标就是构建一个基本概念、基本解题方法知识与解题方法体系,提升学生思维能力,实现“会一题通一类”的目的.“微专题”课型可通过题组设计来实现教学目标.题组中例题的设置和顺序的编排,始终围绕着“微专题”目标进行,最终实现“微专题”教学目的,达到良好的教学效果.题组之间由易到难,由单一到综合,进行对比、变式、多解等分析,使“微专题”涉及的基础知识、基本技能、基本方法和基本思想,在题组中多次出现,形成知识和解题方法体系,再向更高更深化推进.

3、“微专题”课型的设计实例

实例斜三棱柱体积问题

在二轮复习的一次周测中,利用大数据分析,我发现学生对斜三棱柱是学生的概念非常模糊,这个基本概念的缺失,导致立几中常考的体积问题失分严重,于是在二轮复习中插入了《斜三棱柱体积问题》的微专题.

例1(2013年全国I 卷)如图1,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.若AB=CB=2,A1C=求三棱柱ABC-A1B1C1的体积.

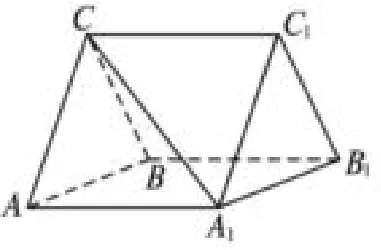
图1

设计意图这就是周测中的题,也是高考原题.测试中学生的典型错误有:(1)以平行四边形BB1C1C为底,等腰△ABC底边上的高为斜棱柱的高; (2)以△ABC为底面,棱AA1为高.以此题为例,首先让学生知道体积问题直接法解题步骤三步走.第一,几何体是什么;第二,底面是谁;第三,谁与底面垂直.让学生明确斜三棱柱的概念,知道棱AA1不垂直底面,底面一定是三角形,要自己去找高并证明,才能计算得到体积.

变式1(2014年全国I卷)如图2,三棱柱ABC -A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.若AC⊥AB1,∠CBB1= 60°,BC= 1,求三棱柱ABC - A1B1C1的高.

图2

法1直接法.运用例1 方法,加以巩固,自己实践求斜三棱柱体积问题直接法的解题三步骤.

法2补成四棱柱.想直接使用条件AO⊥平面BB1C1C求体积,则要将三棱柱补全成四棱柱,两者间体积关比为1:2,从而求得三棱柱的高,这是间接法的一个方向的思路.

法3割成三棱锥.根据等底等高的三棱柱与三棱锥体积关系,可将三棱柱的高转化成三棱锥B1-ABC高的求解,使用等体积法即可.

设计意图体积的问题常常转化为高的问题,所以变式1 变成了求斜三棱柱的高,进一步巩固例1 的直接法,同时拓展学生的思维广度和深度,进行研究间接法,有割和补两个不同的方向,并且联系上三棱锥的等体积法,让学生知道各知识点间的内在联系和逻辑关系.

变式2如图3,三棱柱ABC - A1B1C1中,AA1=2AB= 2,∠BAA1= 60°,D为AA1中点,点C在平面ABB1A1.

图3

(1)求证:BD1⊥平面BCD;

(2)若△CBD是正三角形,求三棱柱ABC -A1B1C1的体积.

设计意图为了让学生构建完整的斜三棱柱求体积的解题方法体系,巩固变式1 中的割补法,补充了变式2.在第(1)的基础上,引导学生如何运用BD1⊥平面BCD,即要直接使用此条件,就必须以三角形BCD为底,则可将三棱锥C -ABD割补至右侧,从而形成一个直棱柱,从而让学生总结得三棱柱的另一个体积公式V=直截面×侧棱.

微专题《斜三棱柱的体积问题》让学生从一个斜三棱柱体积的具体问题出发,抓住基本概念斜三棱柱的底与高,抓住求体积基本方法即直接法和间接法,层层深入,通过题组的变式,最后形成了一个求斜三棱柱体积的解题方法体系,并且能在这个体系基础上让学生继续延展到直三棱柱、三棱锥、斜四棱柱、一般棱柱中去,使学生真正做到在面对具体题目时能根据具体小切口设问,从多角度、多层面理解并重新整合所学知识、灵活地迁移知识,应用于新情境,分析和解决实际问题.

4、效果与反思

二轮复习中与“微专题”配合的是复盘练习,在复盘练习中,我们发现学生做此类题的信心提升,更愿意动笔写,写得更多了,评卷后大数据分析结果显示平均分提高明显.在我们的二轮复习中,有不少的大专题中可插入“微专题”课型,我们实践了《三角形周长与面积的最值》、《几何体的外接球》、《图形背景下的向量问题》、《极坐标与参数方程之选系选方程的技巧》、《线性规划问题》等,都收到不错的效果.