基于有限理性的公交车与私家车交通方式演化博弈

2019-07-17巫娜燕吉选

价值工程 2019年10期

巫娜燕吉选

摘要：为解析城市交通方式结构的形成机理并提出合理的交通管理对策，基于有限理性理论分析了出行者的交通方式选择决策过程，建立了交通方式的演化博弈模型，并对交通方式结构的演化过程进行详细分析。以小汽车与公交车两种交通方式的演化博弈为例，构建了公交分担率随时间变化的动态方程，并基于动态方程参数提出了具体的优化措施，为交通管理者优化城市交通系统结构、制定交通管理政策提供决策信息。

Abstract： In order to analyze the formation mechanism of urban transportation mode structure and propose reasonable traffic management countermeasures， the traveler's mode selection decision process is analyzed based on the theory of bounded rationality， the evolutionary game model of traffic mode is established， and the evolution of traffic mode structure is established. The process is analyzed in detail. Taking the evolutionary game of traffic mode between car and bus as an example， the dynamic equation of the change of bus sharing rate with time is constructed. Based on the dynamic equation parameters， specific optimization measures are proposed to provide decision information for traffic managers optimizing the structure of urban transportation system and developing traffic management policies.

关键词：交通方式结构;有限理性;交通方式选择;演化博弈模型;动态方程

Key words： traffic modes;bounded rationality;traffic mode choice;evolutionary game model;dynamic equation

中图分类号：U491 文献标识码：A 文章编号：1006-4311（2019）10-0022-04

0 引言

出行者交通方式的选择行为一直是城市交通管理领域的核心问题，其选择结果在很大程度上决定了城市的交通方式结构，是交通管理措施和交通政策的制定依据。目前，相关研究已经成为理论研究热点，如国外学者Danisl等[1]提出的随机效用理论离散选择模型，该模型将居民个人社会属性特征，交通服务属性等纳入模型，从而模拟出行者出行选择行为;Koppelman等[2]在分析Nested Logit模型理论的基础上，假定出行者以最大效用为交通方式的选择机制的基础上，建立了四种不同交通方式的Nested Logit模型;Mcfadden[3]在设计问卷调查获取影响居民交通方式选择因素的基础上，基于Mixed Logit建立出行者交通方式选择模型。国内学者赵淑芝等[4]基于长春市居民出行行为的调查数据，构建出行者交通方式选择的MNL模型，得到时间和费用对不同个体交通方式的选择的影响程度不同;贾洪飞等[5]根据对北京市居民的出行调查，建立了公共汽车和小汽车出行选择的二项Logit模型，分析不同收费价格下两种交通方式分担比例的变化;鲜于建川等[6]在考虑交通方式选择集和居民个体差异的基础上，应用多项Logit模型，建立居民通勤方式的選择模型;周雪梅等[7]应用期望偏好（SP）调查方法得到交通方式选择行为特征数据，分析了出行者交通方式的选择行为特征和规律，对公交出行方式需求进行预测。

综上所述，相关研究主要基于出行者完全理性的假设，而现实中的出行者只能在有限理性的条件下，掌握不完全的出行信息进行出行方式选择。因此，研究出行者在有限理性条件下的交通方式决策机制，对理解现实中的交通选择行为非常必要。本文基于有限理性理论，分析出行者在交通方式选择过程中的决策机制，引用演化博弈理论解析城市交通方式结构的形成机理，并建立演化博弈模型，详细分析出行者在不同交通方式之间的博弈过程。

1 有限理性出行者交通方式选择行为

出行者对不同交通方式之间的选择行为，可以理解是交通系统中不同出行者之间的博弈过程，每个出行者交通方式的选择结果，都会影响到其他出行者的效用。根据有限理性理论的假设，出行者在进行交通方式选择时，面临的是一个动态的、复杂的交通系统，并不可能完全掌握其他出行者交通方式选择和路网的实际情况，并不能在开始就找到最优的出行方式，因此出行者的交通方式决策是一个不断学习，反复调整的过程，如图1所示。出行者通过不断的积累经验，通过模仿、学习机制调整自己的出行策略，从而尽可能提高自己的出行效用。出行者这种有限理性的学习、模仿机制经过一段时间的演变，对个体而言，通过不断调整自己的出行方式，从而得到了对个体更有利的策略;对群体而言，城市交通系统中交通方式结构将趋于稳定。

2 交通方式演化博弈模型

演化博弈论是将经济学中的博弈和生物学中的动态演化理论结合起来的一种研究方法，其研究对象是群体的某一状态随时间推移不断变化的现象，目的是为了理解群体演化的动态过程，并解释说明群体如何达到某一状态[8]。一般来讲，一些随机的因素和扰动现象影响群体状态变化，并且群体在状态变化过程中由于群体的选择机制而呈现出来一定的规律性。交通方式结构，是由有限理性出行者根据交通环境的不断变化而不断改变自己的出行方式形成的，呈现一定的规律性。因此，演化博弈理论适用于描述交通方式结构的形成机理。

假定所有出行者均采用单种交通方式出行，i是参与人所有可选择交通方式的集合（i={自行车;步行;公交车;小汽车}），xt （i）代表所有在t阶段采用交通方式的参与人集合，定义状态变量？兹t （i）表示在时间t阶段采用交通方式i出行人群比例，那么：

3 公交车与小汽车演化博弈模型求解

3.1 小汽车与公交车出行成本比较

假定路网中O、D之间共有Q个出行者，且出行者在O、D之间只有公交车、小汽车两种交通方式可以选择。为便于讨论因拥堵给出行者带来额外成本的增加，依据出行成本的分类方法[10]，将公交车与小汽车的出行成本划分为两个类别：一是非拥堵成本。对小汽车出行者而言，非拥堵成本是在道路畅通情况下的出行成本;对公交车出行者而言，非拥堵成本指在道路畅通、公交车内人均空间面积较大下的出行成本;二是拥堵成本。对小汽车出行者，拥堵成本主要指因道路拥堵引起的出行成本的增加;对公交车出行者来说，拥堵成本包括因道路拥堵和车内人均空间面积较小引起的出行成本的增加，具体划分方法如表1所示。

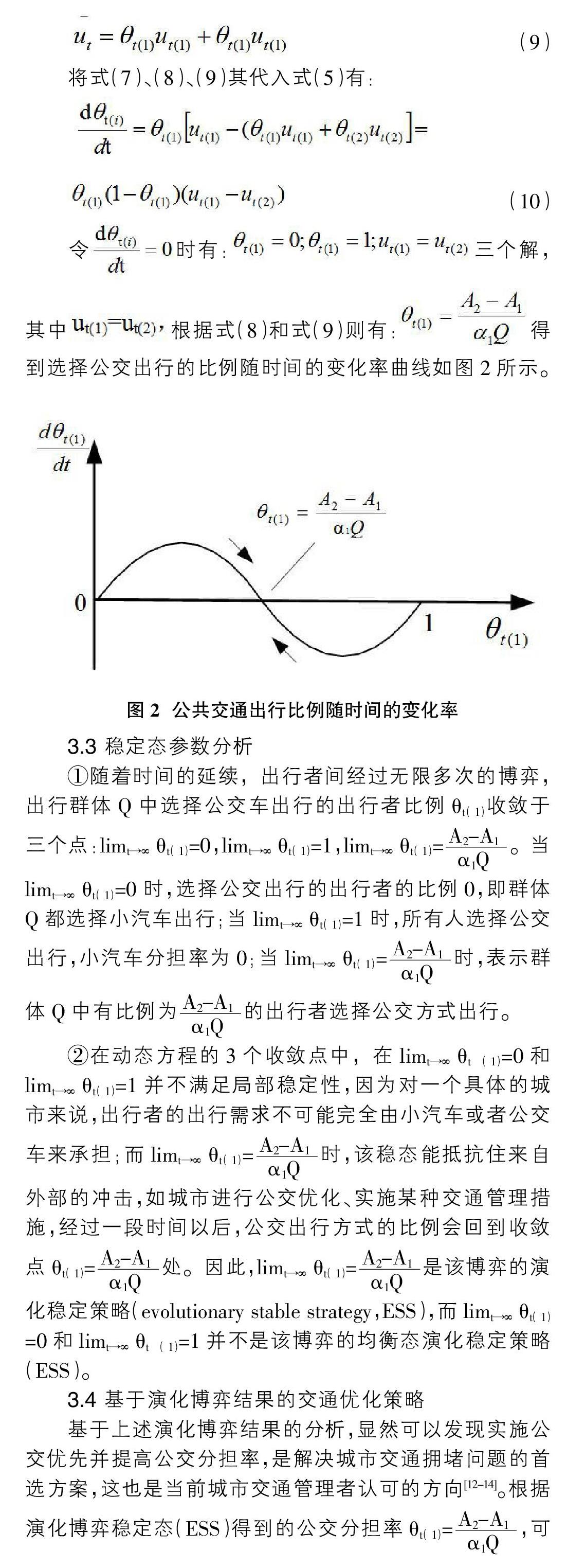
3.4 基于演化博弈结果的交通优化策略

基于上述演化博弈结果的分析，显然可以发现实施公交优先并提高公交分担率，是解决城市交通拥堵问题的首选方案，这也是当前城市交通管理者认可的方向[12-14]。根据演化博弈稳定态（ESS）得到的公交分担t （1）=，可以通过以下三个途径使得公交出行方式比例逐步提高、私家车出行比例逐步降低。

①提高小汽车出行在非拥堵条件下的出行成本，引导居民出行向公共交通转移，具体措施包括：1）通过拍卖等形式提高私家车上牌费，减缓私家车保有量的急剧增长;2）提高中心城区停车收费价格，通过价格杠杆引导通勤出行向公共交通转移。

②降低非拥堵条件下的公交车出行成本，具体措施包括：1）合理设计公交站点，缩短出行者从出发点到站点的步行时间及下车至目的地的步行时间;2）分层规划城市公交线网，减少出行者的换乘次数，缩短换乘时间;3）对出行需求大的公交线路，增大公交车发车频率，提高公交车准点率，从而减少公交出行者的候车时间;4）提高公交车运营速度，缩短出行者车内时间;5）出台公交票价优惠措施，从而降低公出者的出行成本。

③降低公交车内的拥堵成本，即降低公交车内的拥挤系数。城市交通管理部门应加大对公交的支持力度，通过发展智能公交调度系统，确保公交运行的可靠性，并逐步完善公交车型结构，提高公交出行者的舒适度。

4 结束语

本文基于有限理性理论分析了出行者的交通方式选择行为，运用演化博弈理论建立了出行者的交通方式选择模型，分析了交通方式结构的演化过程，并重点探讨了公共交通与小汽车的两种交通方式的选择演化博弈模式，得到公交分担率随时间变化率的动态方程。通过对动态方程参数的分析得出：通过提高小汽车出行成本、降低公交出行成本，使得系统中选择不同交通方式的用户比例向城市交通管理者期望的方向演化。

参考文献：

[1]McFadden D. Disaggregate behavioral travel demands RUM sidea 30-year retrospective[C]. Intemational Association for Travel Behavior Conference， Australia， 2000.

[2]Koppelman F S， Wen C H. Alternative nested logit model： structure， porperties and estimation[J]. Trasportation Research B， 1998， 32（5）：289-298.

[3]Mcfadden D L， Train K. Mixed MNL Models for Discrete Response[J]. Journal of Applied Econometrics， 2000， 15（5）： 447-470.

[4]趙淑芝，赵贝，朱永刚. 基于 SP 调查的出行方式选择模型与公交优先政策[J].吉林大学学报（工学版），2009，39（2）：187-190.

[5]贾洪飞，龚勃文，宗芳.交通方式选择的非集计模型及其应用[J].吉林大学学报（工学版），2007， 37（6）：1288-1293.

[6]鲜于建川，隽志才.考虑选择集和个体差异的交通方式选择分析[J].统计与决策，2009，14：100-102.

[7]周雪梅，张显尊，杨晓光，劳云腾.基于交通方式选择的公交出行需求预测[J].同济大学（自然科学版）， 2007，35（12）：1627-1631.

[8]孙庆文，陆柳，严广乐，车宏安.不完全信息条件下演化博弈均衡的稳定性分析[J].系统工程理论与实践，2003，7：11-16.

[9]张维迎.博弈论与信息经济学[M].上海：上海人民出版社，2004.

[10]胡永举.城市居民出行成本的量化方法研究[J].交通运输工程与信息学报，2009，3（7）：5-10.

[11]王海洋，周伟，王元庆.旅客行为时间价值确定方法研究[J].公路交通科技， 2004，21（8）：134-137.

[12]陈方，戢晓峰. 城市交通政策对交通公平的影响分析[J]. 昆明理工大学学报（社会科学版），2011，11（2）：7-10.

[13]陈方，戢晓峰.论城市交通的伦理维度[J].昆明理工大学学报（社会科学版），2010，10（5）：1-5.