基于黏性流理论对平板受波浪冲击的两相流数值研究
2019-07-17毛鸿飞李芳成吴光林
毛鸿飞, 李芳成, 吴光林, 严 谨
基于黏性流理论对平板受波浪冲击的两相流数值研究
毛鸿飞, 李芳成, 吴光林, 严 谨
(广东海洋大学海洋工程学院,广东 湛江 524088)
【目的】研究波浪作用下位于水面上方的刚性平板所受冲击力特征,讨论数值计算结果与实验结果的差异。【方法】基于黏性流理论,采用有限体积(VOF)方法建立两相流数值波浪水槽模型,对潜堤地形上波浪传播变形和淹没水平圆柱在波浪作用下受力问题进行数值验证,对平板受波浪冲击作用进行数值模拟,通过平板下表面测点上点压力数值结果特征分析以及与前人实验数据对比,讨论结果差别原因,分析结果特征形成机理。【结果】潜堤地形上波浪传播变形的数值结果和前人实验数据吻合较好;对于波浪作用下平板的受力,相比前人实验数据,冲击力数值结果更大,且呈现出更稳定的周期性特征,沿波浪传播方向平板上的冲击力先增大后减小。【结论】建立的数值模型对波浪与结构物相互作用问题的模拟有高的精确性和稳定性。
数值模拟;波浪水槽;平板;冲击力
平板结构在海洋工程中的应用非常广泛,如近海采油平台、桩基础码头和近岸输油管桥等,这些结构物平底高程较低,其生产安全性受波浪冲击作用影响较大。波浪对结构物的冲击作用过程复杂,涉及到波浪非线性、瞬时效应、流体黏性、湍流、气液掺混等因素,是当今海洋工程水动力学研究的难点问题。
早期对平板受波浪冲击作用的研究多采用理论解析和物理模型实验方法。Kaplan等[1-3]对通过动量和附加质量计算出了平板上垂向冲击力的解析式;任冰[4]对波浪冲击作用下平板上的冲击力开展了物理实验研究,给出了平板下方点压力时间历程;参考Wagner[5]对平板冲击的理论解析形式,Baarhom等[6-8]采用理论解析和物理模型实验方法针对线性波浪冲击作用下平板所受冲击力以及浮式平台受力和运动响应等问题开展了研究;Wang和Ren[9-10]先后针对规则波和不规则波作用下平板所受到的冲击力开展了物理实验研究。早期的势流理论解析研究准确性较差,且无法考虑流体黏性的影响,物理模型实验由于实验设备的高频捕捉能力缺陷也无法准确稳定的测量波浪冲击力,且由于实验条件局限,对于冲击力测量也容易产生误差。
随着计算机技术的发展,对波浪作用于平板的相关数值模拟研究也相继开展。Buchner和Cozinijn[11]以及Faltinsen等[12]均采用边界元方法,考虑非线性自由面和物面条件,对平板的越浪和受波浪冲击问题开展了数值模拟研究;Wang和Ren[13]以及任冰等[14]应用基于有限体积法建立的数值水槽模型,对斜坡地形上,椭圆余弦波冲击作用下平板受力问题开展了数值模拟研究,讨论了结构物和静水面距离对冲击力的影响;Baarholm等[15]采用边界方法,对波浪对平台的冲击作用开展了数值模拟研究,并分析了平台运动响应的特征;Li等[16]采用Navier-Stokes方程求解器对波浪对平板下侧冲击过程进行了的数值计算,对波浪破碎对冲击力的影响进行了讨论;Ren和Wang[17]采用有限体积法针对不规则波对平板的冲击作用进行了数值计算;Sun等[18]采用光滑粒子法建立了数值水槽模型,并对波浪冲击作用下平板受力进行了数值计算,其结果与前人实验数据接近。上述基于势流理论对平板受波浪冲击作用的研究均没有考虑流体黏性影性,而目前基于黏性流理论的相关研究报道中未使用湍流模型,未考虑湍流影响,且单相流的数值模拟也无法考虑气液掺混问题。
针对上述前人对平板受波浪冲击作用研究的局限性,本研究在OpenFOAM开源平台基础上进行二次开发,基于黏性流理论,采用有限体积方法,建立两相流数值波浪水槽模型,采用RNG-湍流模型进行湍流封闭,并应用该模型对非线性波浪作用下,初始时刻位于水面上方的平板所受波浪冲击力进行数值计算研究;对潜堤地形上波浪传播变形和波浪作用下淹没水平圆柱受力进行计算,通过与实验数据对比验证数值模型的准确性;通过对波浪冲击作用下平板下表面多个测点处压力的计算,查找与前人实验数据的差别,讨论差别产生的原因,并分析冲击力的特征,揭示其形成机理,以期为海洋工程结构物的设计和安全生产提供理论依据和参考。
1 两相流数值模型的基本原理
1.1 控制方向和湍流模型
以Navier-Stokes方程为数值模型的控制方程,张量形式的连续性方程和动量守恒方程为:


式中,u为流体在方向上的速度,为流体的密度,为时间,为重力加速度,为压强,μ=+μ为有效动力学黏性系数,其中,为流体黏性系数,μ为湍流黏性系数。
采用RNG湍流模型进行湍流封闭,湍动能和耗散率的对流输运方程分别为:

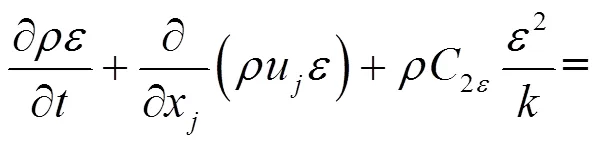
式中,1ε= 1.42,2ε= 1.68,σ= 0.72和σ= 0.72为模型常数。
1.2 自由面捕捉方法
采用VOF方法进行自由面捕捉。单元密度和黏性系数表示为:




1.3 边界条件
两相流数值水槽模型采用速度边界法和松弛方法来实现造波和消波,边界和松弛区如图1所示。入口边界为速度边界条件(流体速度按相应波浪理论给定,初始压强为*/= 0,其中* =−为动态压强,为某点到自由面的距离),出口边界、底边界以及水槽中固定结构物边界均为不可滑移边界条件(初始速度和压强为u= 0,*/= 0),顶边界为可自由进出边界条件(初始速度和压强为∂u/= 0,* = 0)。图中松弛区I的功能是协助波浪生产和吸收从结构物的反射浪,松弛区II的功能是消除消波出口边界的反射波。松弛区内,以解析形式修正数值求解[20]。松弛区内的流体速度和体积分数的修正形式为:

式中,代表修正的物理量,下标、和分别表示物理量的目标值、解析值和计算值,δ和χ为松弛函数,定义为:


图1 边界和松弛区示意
采用五阶Stokes波浪理论生成非线性波浪,自由面高度为:
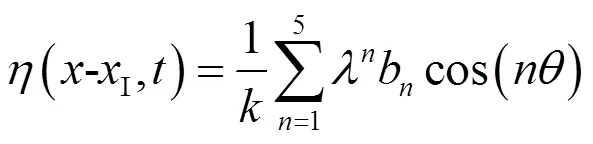

式中,I为造波区宽度,为阶数,为波数,=为无量纲波幅,为波幅,=(−I)−ω+为相位角,为波浪角频率,为初相位,B为与水深和波数相关的无量纲参数。水平和垂向速度则分别为:



式中,0和A为与水深和相关的无量纲参数。上述无量纲参数形式可参考Fenton[21]提出的五阶Stokes波浪理论。
1.4 波浪力计算
结构物上的波浪力计算式为:
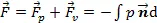

2 数值模型准确性验证
为了验证数值波浪水槽模型对波浪与结构物相互作用计算的准确性,分别对潜堤地形上波浪的传播变形问题以及淹没水平圆柱在波浪作用下受力问题开展数值验证。
2.1 潜堤地形上波浪传播变形验证
波浪在遇到潜堤地形时,波浪传播过程中会发生波面变形现象,呈现出很强的非线性特征。Beji和Battjes[22]在潜堤地形上开展了波浪传播的物理模型实验。本验证计算选取的水槽几何尺寸、波浪参数、潜堤地形以及浪高仪的位置等均参照前人的物理实验设置,计算域示意如2图所示。水槽长度为24 m,水深= 0.40 m,潜堤底端距离波浪生成区6.0 m,距离消波区7.0 m,潜堤顶端与静水面位置距离为0.1 m,潜堤迎浪侧坡度为1∶20,背浪侧坡度为1∶10,高度为0.3 m。采用五阶Stokes波浪理论生成非线性波浪,入射波浪周期为= 2.02 s,波幅为= 0.01 m,波浪造波和消波松弛区宽度分别取为2.5和3.0(为入射波波长,下文同)。根据物理实验中浪高仪的情况,数值计算中浪高仪的位置见表1。

图2 潜堤上波浪传播计算域

表1 浪高仪位置
将波面时间历程数值结果与Beji和Battjes[22]的物理实验结果对比,以浪高仪G3 ~ G11为例,各浪高仪处波面对比如图3所示。由图中结果对比可见,浪高仪G3位置,本研究数值结果与实验结果吻合良好,波浪在传播过程中并没有明显的变形,波面未呈现强非线性特征,这是因为波浪传播还没受到潜堤地形的影响。浪高仪G4位置,本研究数值结果与实验结果吻合良好,波浪传播至潜堤迎浪坡上,波面开始呈现出一定的非线性特征。浪高仪G5 ~ G11位置,由于潜堤对波浪传播有显著影响,波浪传播过程出现了明显的变形,体现出强非线性特征。总体上,本研究的数值结果与前人的实验数据吻合较好,这证明了本研究建立的数值模型对于波浪稳定传播和波浪传播遇结构产生波面形态变化问题的计算具有较好的准确性。

图3 潜堤地形上波浪传播对比
2.2 潜堤地形上波浪传播变形验证
Chaplin[23]针对淹没水平圆柱在波浪作用下的受力问题开展了物理模型实验,本验证计算选取的水槽几何尺寸、波浪参数、圆柱尺寸和垂向位置等均参照该物理实验设置,计算域示意如4图所示。水深= 0.85 m,圆柱半径= 0.051 m,其轴心距离静水面= 0.102 m,圆柱轴心分别距离造波区和消波区1.65和4.0。采用五阶Stokes波浪理论生成非线性波浪,无量纲入射频率表示为= 0.206,波幅为= 0.65 ~ 2.79 m,波浪造波和消波松弛区宽度分别取为2.5和3.0。

图4 波浪作用于水平淹没圆柱计算域
将波浪力数值结果与Chaplin[23]的物理实验数据对比,如图5所示。图中,波浪力和波幅分别采用无量纲形式/()和/表示。由图中结果对比可见,对于水平波浪力和垂向波浪力,本研究数值结果与前人实验数据均吻合较好,这证明了本研究建立的数值模型对于波浪作用下结构物所受波浪力的计算具有良好的准确性。
3 数值计算和结果分析
3.1 算例及计算参数设置
参考任冰[4]对平板受波浪冲击作用开展的物理实验,本研究数值计算所选取的水槽尺寸和平板位置等计算设置如图6所示。平板下表面与静水面距离= 1.0 cm,平板左侧与造波区域距离为4.6,与消波区距离为4.0。波浪生成区和消波区长度分别为2.5和3.0,水深= 0.60 m。波浪参数为:入射波周期= 1.2 s,波幅= 7.5 cm。

图5 波浪力随A/r变化趋势

图6 平板受波浪冲击计算域示意
为考察波浪作用下平板所受冲击作用,以其下表面的点压力值进行描述,即需在平板下表面布置压强测点。平板的几何尺寸及其下表面压强测点布置如图7所示。平板长为100 cm,厚度为2.0 cm,其下表面布置11个压强测点,间距为9.0 cm。
数值计算中,网格设置原则为一个波长内划分单元个数为100,一个波高范围内划分单元数量为20,平板周围网格设置加密区,沿平台轮廓单元数量为220;初始时间步长为/1 000,并进行自适应调整,计算时长为15 s。

图7 平板下方点压力测点分布示意
3.2 数值结果和讨论
为了考察波浪作用下平板所受波浪力的数值结果特点,将一些测点处数值计算所得点压力时间历程与任冰[4]的实验数据进行比较。
平板各测点的点压力数值计算结果和实验数据的对比如图8所示。图中,曲线形态体现为尖锐峰值部分为冲击力,其余部分为惯性力和速度力的合力。从对比情况可见,波浪对平板有明显的冲击作用,冲击力的特点是其正垂向峰值相较于的惯性力和速度力部分较大,且作用时间很短。本研究的数值结果中,冲击力的峰值在多个周期内比较接近,即冲击力大小相对稳定;而相比之下,前人的实验结果则体现出多个周期内冲击力大小变化幅度较大的特点。这是由于在物理模型实验中,可能存在一些偶然因素影响实验结果,如波浪水槽断面实验的误差,应力感应装置的捕捉频率是否满足等。此外,数值结果和实验数据在惯性力和速度力部分也有一定差别,在G5~G11测点处尤为显著,数值结果的正垂向惯性力和速度力相对稳定,负垂向力较小;而在实验数据中,正垂向力较小,且负垂向力出现了较多力的波动。这可能是物理模型实验中,平板下表面的不平滑,导致水对平板下表面有明显的负向附着力。

图8 本研究数值计算与前人物理实验点压力历时曲线
为了便于比较冲击力的大小,将上述数值计算和物理实验所得冲击力的极值取平均值,以P表示,在各测点处进行对比,如图9所示。从图中对比情况可见,总体上,前人的实验结果相比本研究的数值结果偏小。两组结果在水平正方向上(测点的水平位置,设中点处为= 0)的变化趋势也有差别。数值研究表明,在波浪作用于平板初期,由于板侧的阻碍作用,G1~G3过程的冲击力增大;在波浪继续传播,持续作用于平板过程中,由于波浪的反射和能量耗散,波浪在水平方向传播过程中,随着测点在水平方向上靠后(G3 ~ G11),冲击力呈现逐渐减小的趋势。

图9 冲击力平均值
4 结论
基于黏性流理论,采用有限体积方法建立了可以模拟平板受波浪冲击作用的两相流数值模型,并采用RNG-湍流模型进行湍流封闭。针对潜堤地形上的波浪传播变形和波浪作用下淹没水平圆柱受力问题,将数值结果和前人实验数据对比,验证了数值模型对波浪与结构物相互作用问题模拟的准确性。对于平板下表面所受波浪力,相比前人的实验结果,本研究的冲击力数值结果在多个周期内呈现更接近和稳定的特征。数值研究发现,由于侧壁的阻碍作用和波浪作用于平板过程中的能量损耗,在水平方向上随着测点靠后,冲击力呈现先增大后减小的趋势,且各测点上的冲击力相比实验结果较大。
[1] KAPLAN P, SILBERT M N. Impact force on platform horizontal members in the splash zone[C]. Dallas: Proceedings of Offshore Technology Conference, 1976, 749-758.
[2] KAPLAN P. Wave impact force on offshore structures: re-examination and new interpretations[C]. Houston: Proceedings of Offshore Technology Conference, 1992, 6814: 79-86.
[3] KAPLAN P, MURRAY J, YU W. Theoretical analysis of wave impact forces on platform deck structures[C]. Copenhagen: International Conference on Offshore Mechanics and Arctic Engineering, 1995, 1(A): 189-198.
[4] 任冰. 随机波浪对不同接岸型式码头上部结构的冲击作用研究[D]. 大连: 大连理工大学, 2003.
[5] WAGNER H. Uber stoss-und gleitvorgange an der oberflache von flussigkeiten[J]. Zeitschrift Für Angewandte Mathematik und Mechanik, 1932, 12(4): 193-215.
[6] BAARHOLM R, FALTINSEN O M. Experimental and theoretical studies of wave impact on an idealized platform deck[C]. New York: Proceedings of International Conference on Hydrodynamics, 2000, 181-186.
[7] BAARHOLM R, FALTINSEN O M, HERFJORD K. Water impact on decks of floating platforms[J]. Practical Design of Ships and other Floating Structures, 2001, 1: 621-627.
[8] BAARHOLM R. Theoretical and experimental studies of wave impact underneath decks of offshore platforms[D]. Trondheim: Norwegian University of Science and Technology, 2001
[9] WANG Y X, REN B. Experimental study of wave slamming[C]. Lisbon: Proceedings of International Conference on Ocean, Offshore and Arctic Engineering,1998, OMAE98-0403.
[10] WANG Y X, REN B. Experimental study of irregular wave slamming[C]. Kyushu: Proceedings of International Ocean and Polar Engineering Conference, 2002, 492-495.
[11] BUCHNER B, COZIJIN J L. An investigation into the numerical simulation of green water[J]. Marin, 1997, 113-125.
[12] FALTINSEN O M, GRECO M, LANDRINI M. Green water loading on FPSO[J]. Journal of Offshore Mechanics and Artic Engineering, 2002, 124(2): 94-103.
[13] WANG Y, REN B. Numerical simulation of wave slamming by turbulent model[C]. Hong Kong: Proceedings of International Conference on Ocean Science and Technology,1997, 251-259.
[14] 任冰, 王永学. 非线性波浪对结构物的冲击作用[J]. 大连理工大学学报, 1999, 39(4): 562-566.
[15] BAARHOLM R, FALTINSEN O M. A boundary- element method for solving water impact on a platform deck[C]. Lisbon: Proceedings of Offshore and Arctic Engineering Conference, ASME, 2001.
[16] LI T Q, TROCH P, DEROUCK J, et al. Numerical simulation of water wave impacts on the underside of a horizontal deck using a Navier-Stokes solver[J]. Coastal Engineering, 2004, 4: 4100-4112.
[17] REN B, WANG Y X. Numerical simulation of random wave slamming on structures in the splash zone[J]. Ocean Engineering, 2004, 31: 547-559.
[18] SUN Z C, LIANG S X, REN X F, et al. A two-phase simulation of wave impact on a horizontal deck based on SPH method[J]. Procedia Engineering, 2015, 116: 428-435.
[19] WELLER H G, TABOR G, JASAK H, et al. A tensorial approach to computational continuum mechanics using object oriented techniques[J]. Journal of Computational Physics, 1998, 12 (6): 620-631.
[20] JACOBSEN N G, FUHRMAN D R, FREDSØE J. A wave generation toolbox for the open-source CFD library: Open FOAM[J]. International Journal for Numerical Methods in Fluids, 2012, 70: 1073-1088.
[21] FENTON J D. A fifth-order Stokes theory for steady waves[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1985, 111: 216-234.
[22] BEJI S, BATTJES J A. Experimental investigation of wave propagation over a bar[J]. Coastal Engineering, 1993, 19: 151-162.
[23] CHAPLIN J R. Non-linear forces on a horizontal cylinder beneath waves[J]. Journal of Fluid Mechanics, 1984, 147: 449-464.
Two-phase Numerical Examination of Wave Impact on a Horizontal Deck based on the Viscous Fluid Theory
MAO Hong-fei, LI Fang-cheng, WU Guang-lin, YAN Jin
(,,524088,)
【Objective】This study focuses on the slamming forces on a rigid horizontal deck over free surface under wave action. The reasons for the discrepancies between the numerical results and the previous experimental data are discussed. 【Method】A two-phase numerical wave tank model is developed based on the viscous fluid theory using the finite volume method. The accuracy of the NWT model is validated by considering wave propagation over a bar and wave force on a submerged horizontal circular cylinder. The pressure on the low surface of the horizontal deck under wave impact is studied compared with previous experimental results. The discrepancies among the results are found, corresponding reasons are analyzed, and the characteristic mechanisms of the pressure are revealed. 【Result】The validation of wave propagation over a bar shows that the numerical results are in good agreement with the previous experimental data. The study on the slamming forces on the deck shows that the numerical results first increase, and then gradually decrease along the direction of wave propagation. Compared with the experimental data, the slamming forces predicted by the numerical simulation are larger and more stable in multiple periods. 【Conclusion】The numerical model works well in simulating wave-structure interaction.
numerical simulation; wave tank; horizontal deck; slamming force
TV139.2+6
A
1673-9159(2019)04-0073-08
10.3969/j.issn.1673-9159.2019.04.011
2019-04-16
广东省自然科学基金(2017A030313275), 广东海洋大学科研启动费项目(R19024)
毛鸿飞(1985-),男,博士,讲师,研究方向为波浪与结构物的相互作用。E-mail:maohongfei-gdou@qq.com
严谨(1974-),男,博士,教授,研究方向为海洋工程结构物水动力特性。E-mail: d3219yan@sina.com
毛鸿飞,李芳成,吴光林,等. 基于黏性流理论对平板受波浪冲击的两相流数值研究[J]. 广东海洋大学学报,2019,39(4):73-80.
(责任编辑:刘朏)
