内河桥梁船撞损伤影响因素及影响规律数值模拟分析

2019-07-17袁龙文郝艳广韩劲龙曾庆刚程海潜

重庆理工大学学报(自然科学) 2019年6期

袁龙文，郝艳广，韩劲龙，曾庆刚，程海潜

(1.武汉港湾工程质量检测有限公司，武汉 430000； 2.海工结构新材料及维护加固技术湖北省重点实验室，武汉 430000；3.湖北交通职业技术学院，武汉 430000)

随着水运业务突飞猛进的增长以及水运船舶大型化的发展趋势，船舶对桥梁的影响愈发增大，桥梁受到船舶撞击的可能性以及撞击后造成的后果也逐渐增大[1～3]。如2007年，江西省九江市跨长江大桥受到3 000 t级船舶撞击倒塌，造成5死26重伤的重大事故[4]。因此，研究桥梁受船舶撞击的作用规律，并针对性地提出解决措施，对保障桥梁安全至关重要[5]。本文拟借助LS-DYNA三维有限元计算软件，以润扬长江大桥为研究实例，撞击船舶选择最不利船舶(3 000 t级)，建立三维数值模型，从桥墩混凝土强度、配筋率、船舶行驶速度等方面分析对桥墩撞击的具体影响。

1 模型建立

1.1 船舶有限元模型

选择长江下游(镇江段)实际最大运输船型(3 000 t级)作为撞击船型，船型尺度为95.0 m×16.2 m×3.2 m，根据现场踏勘，船舶船体结构采用Q235钢材，撞击船型有限元模型及钢材本构示意模型见图1，船体网格间距取2.0 m，局部区域进行加密处理，加密区域网格间距取1.0 m，整个船舶模型共有2 462个网格。船与桥墩接触采用Kelvin黏弹性本构模型。

图1 撞击船型有限元模型及钢材本构示意模型

1.2 桥墩有限元模型

润扬长江大桥桥墩采用墩柱式结构，承台采用长和宽均为6.8 m的矩形结构，承台下部桩基直径为1.6 m，长12.8 m，承台上部为实心独柱式墩。对实心独柱式墩、承台、桩基3部分结构均采用刚体结构进行模拟。桥墩有限元模型见图2。桥墩损伤本构模型采用Rousselier模型，在模型中采用梯度依赖损伤原理，并考虑损伤材料的质量密度ρ低于无损伤时的材料密度ρ0。

图2 桥墩有限元模型

2 模型计算及分析

根据《江苏省航道管理条例》及《内河通航标准》(GB—50139)，桥墩承台顶高程应设置在设计航道底高程以下，因此桥墩承台基本没有受撞击风险[6-9]，这也与笔者对2017年全国各类桥梁撞击事故实际调查结果相符。因此，本文拟从桥墩混凝土强度、配筋率、船舶行驶速度、撞击角度等方面分析对实心独柱式墩撞击的具体影响。

2.1 混凝土强度对桥墩损伤的影响分析

桥墩模型选择砼结构损伤本构模型[10]，3 000 t级货船撞击速度取5 m/s，且假设撞击船舶为恒定速度，配筋率取2%，船舶撞击角度取80°，撞击点设在承台顶部以上5 m处，分析不同混凝土强度下(共取C30、C40、C50以及C60四组工况)，船舶对实心独柱式墩撞击损伤结果。各工况下撞击力、桩顶位移、墩顶位移、撞击后下部结构损伤结果依次见图3～6。各工况下撞击结果对比见表1。

图3 船舶撞击力历程曲线

图4 桩顶位移历程曲线

图5 墩顶位移历程曲线

图6 桥墩下部结构损伤分布

表1 各混凝土强度下撞击结果比较

分析图3～6，并结合表1结果可知：

1) 船舶对桥墩的撞击力峰值随混凝土强度增大而单调递增，与C30强度混凝土相比，C40、C50、C60撞击力峰值分别增大3.4%、10.8%、14.9%，可见混凝土强度增大将导致撞击力峰值单调提高。

根据文献[11]中的经验公式对撞击力峰值与混凝土强度的关系进行拟合，可得到回归公式：

Fmax=(0.8285+0.0047×q)FC30

(1)

式中：Fmax为撞击力峰值；q为混凝土抗拉强度；FC30为C30混凝土对应的撞击力峰值。根据验证，式(1)的拟合值样本与实际计算值样本相关系数为0.92，残差平方和为0.87，可见式(1)拟合效果较好，能很好地反映撞击力峰值与混凝土强度的关系。

2) 分析船舶撞击力历程曲线可知，各工况下的撞击力历程曲线及历程变化都较为相似，只是在峰值时间范围(0.4 s附近)内有所差异，根据统计，差异幅度均小于10%。

3) 分析图4、图5可知，桥墩混凝土等级对桩顶位移、墩顶位移基本没有影响。

2.2 配筋率对桥墩损伤的影响分析

桥墩模型选择砼结构损伤本构模型，船舶撞击速度取5 m/s，且假设撞击船舶为恒定速度，船舶撞击角度取80°，撞击点设在承台顶部以上5 m处，混凝土强度选择C40；分析不同配筋率下(共取0.5%、1%、2%、5%、10%、15%、20%、25%八组工况)船舶对实心独柱式墩撞击损伤结果。各工况下撞击力、桩顶位移、墩顶位移、撞击后下部结构损伤结果依次见图7～10，其中由于本次工况取数据样本较多，因此图7～10中只反映5%、10%、15%工况样本。各工况下撞击结果对比见表2。

图7 船舶撞击力历程曲线

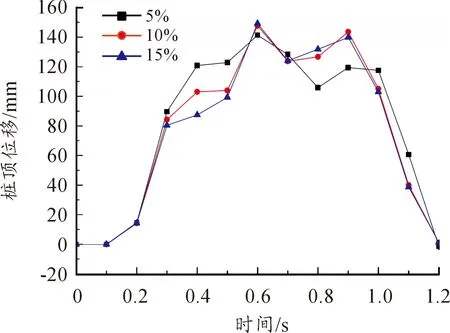
图8 桩顶位移历程曲线

图10 桥墩下部结构损伤分布

表2 各配筋率下撞击结果比较

分析图7～10，并结合表2结果可知：

1) 船舶对桥墩的撞击力峰值随配筋率的增大而增大，其中配筋率在1%以下时，撞击力峰值随着配筋率的增大迅猛增加，在配筋率大于2%以后，撞击力峰值基本稳定，随配筋率变化幅度较小。与2%配筋率工况相比，0.5%与1%配筋率的工况撞击力峰值分别减少14.77%与6.71%。而在配筋率从2%增大至25%时，撞击力峰值的最大增幅仅有5.37%。根据文献[11-12]中经验公式对撞击力峰值与配筋率的关系进行拟合，可得到回归公式：

Fmax=(0.811+0.021ρ-0.000 85ρ2)Fρ2%

(2)

式中：ρ为配筋率；Fρ2%为2%配筋率工况下对应的撞击力峰值。根据验证情况，式(1)的拟合值样本与实际计算值样本相关系数为0.85，残差平方和为0.73，可见式(2)拟合效果较好，呈显著的二次线性关系，能很好地反映撞击力峰值与配筋率的关系。

2) 各工况下撞击力曲线变化趋势基本稳定，只是峰值出现时间稍有偏差，配筋率小的工况下，桥墩下部结构峰值出现时间略有滞后。

3) 分析图8与图9可知，当配筋率小于2%时，下部位移较大；在配筋率为0.5%时，桩顶和墩顶的最大位移分别达到247 mm以及447 mm；而在配筋率大于2%时，桩顶和墩顶的最大位移分别降至147 mm与337 mm以下，且桥墩位移趋于稳定，受配筋率变化影响幅度较小。

4) 2%配筋率是桥墩受到撞击力，桥墩位移受配筋率影响程度的临界值。当配筋率小于2%时，桥墩受到撞击力、桥墩位移受配筋率变化影响非常大；当配筋率大于2%时，这两项特征值趋于稳定，几乎不再变化。

2.3 船舶速度对桥墩损伤的影响分析

文献[13]指出，船舶速度是美国现行规范下计算船舶撞击力的核心指标之一。为了分析不同船舶速度对桥墩损伤的影响，桥墩模型选择砼结构损伤本构模型，混凝土强度选择C40，配筋率选择2%，船舶撞击角度取80°，撞击点设在承台顶部以上5 m处，分析不同船舶速度下(共取2.5、5、7.5、10 m/s四组工况)，船舶对实心独柱式墩撞击损伤结果。各工况下撞击力、桩顶位移、墩顶位移、撞击后下部结构损伤结果依次见图11～14。各工况下撞击结果对比见表3。