基于双边匹配博弈模型的马拉松赛事报名主体间关系研究

毕红星

(东北财经大学体育经济研究中心，辽宁 大连 116025)

1 引言

马拉松赛事是举办方和参赛者为体现马拉松运动价值而安排的一种商业合作活动。本文中的马拉松赛事特指中国大陆地区的达到国际田径联合会(IAAF)认证标准的金标赛事。因为这些赛事偏重于比赛本身的组织能力，比如计时系统、裁判等级、赛道情况、保障体系、参赛运动员水平、比赛影响力等综合水平。马拉松赛事举办方参与办赛，一方面通过提高竞技运动水平和推动全民健身运动开展而获得的社会效益，另一方面是以赛事产业链(包括赛事本体产业、赛事载体产业、赛事媒体产业、赛事衍生产业)形式来促动马拉松路跑产业发展进而获取经济效益。而参赛者参与马拉松赛事除了完成所规定的比赛赛程，还利用马拉松赛事平台来满足身心要求的体育文化体验。实践表明，马拉松赛事举办与参赛关系的建立是个双向选择的过程，需要举办方和参赛者一致同意才能达成。

在达成马拉松赛事正常运行的状态之前，确定谁来参赛和选择谁来确定参赛，是摆在马拉松赛事举办方和参赛者之间非常关键的问题，筛选的结果直接影响着马拉松赛事的成功举办及其收益的高低。若想使马拉松赛事功能最大化表现出来，马拉松赛事举办方与参赛者双方都会积极地依据自身的偏好来确定另一方建立参赛双边关系。这种双边选择问题与Gale和Shapley研究的“学校录取问题”的双边匹配模型的思想非常一致，其共同点都是以实现个体效用最大化为目标，进而依据各自偏好选择对方形成配对关系。Gale和Shapley通过研究“学校录取问题”的研究创立了双边匹配博弈模型。双边匹配博弈模型的理论基础是匹配博弈理论，匹配博弈理论的基本类型可分为一对一、多对一、多对多三种类型，双边匹配博弈模型归类为匹配博弈理论类型中的“一对一”。因此，双边匹配博弈模型是解决马拉松赛事报名问题的有效路径。在马拉松赛事报名的双边匹配博弈中，赛事举办方选择与赛事相匹配的参赛者给予参赛资格的认定，而赛事参赛者则选择与其匹配的马拉松赛事进行参赛。

利用Citespace的研究方法对国外和国内关于“马拉松(Marathon)”方面文献进行分析。首先，在Web of Science数据库中，以“Marathon”为主题词进行检索，得到3484篇相关文献，关键词聚类表现出如下19个国外马拉松研究热点：#0：Triathlon(铁人三项)，#1：Inflammation(炎症)，#2：Cardiac Fatigue(心脏疲劳)，#3：Man(成年男子选手)，#4：Exercise-associated Hyponatremia(运动相关性低钠血症)，#5：Prevention(预防)，#6：Heat Stroke(中暑)，#7：Wear(参赛服饰)，#8：Mass Casualty(集体事故)，#9：Glucosinolates(硫代葡萄糖苷)，#10：Vitamin E(维生素E)，#11：Ventilation(通气)，#12：Environment(环境)，#13：Vasculature(血管状)，#14：Cortisol(皮质醇)，#15：Ctni(心肌钙蛋白I)，#16：Terrorism(恐怖主义)，#17：Maximal Oxygen Uptake(最大摄氧量)，#18：Atrial Fibrillation(心房颤动)，#19：Marathon Running(马拉松赛跑)。其次，在CNKI数据库中，以“马拉松”为主题词，选择核心期刊和CSSCI期刊类别，获取的257篇有关文献，关键词聚类分析得出国内马拉松研究热点表现为8个：#0：体育管理，#1：高原训练训练方法，#2：路跑赛事，#3：体育工作者，#4：巴塞罗那奥运会，#5：媒体融合，#6：全民健身。

综上所述，目前，对马拉松赛事举办与参赛问题的研究主要包括：马拉松赛事组织价值的实现(覃雪芹，2017)、马拉松赛事持续参与行为形成机制(何平香，2017)、马拉松赛事定位(石春健，2016)、马拉松赛事参赛者服务(李齐，2017)、马拉松赛事信息系统(李战克，2017)、马拉松赛事举办的支持系统(韩格格，2016)、马拉松赛事竞赛组织风险与评估(石磊，2017)。然而，对于双边匹配博弈模型在马拉松赛事举办与参赛领域的研究则特别鲜见。本文试图对马拉松赛事举办与参赛问题研究以跨界和学科交叉的方式来进行，引入匹配博弈理论，以马拉松赛事的具体特征为研究基础，尝试构建双边匹配博弈模式，探析举办方和参赛者双方的双向选择关系，梳理模型求解的过程。

2 匹配博弈理论的阐述

当在市场中没有价格或者价格受到限制的情况下，市场则不能依赖价格来实现配置资源与配对交易双方，近代经济学从博弈论研究的视角回答了市场的有效性以及稳定匹配的问题。1962年，Gale和Shapley在《美国数学月刊》(American Mathematical Monthly)上发表了“College admissions and the stability of marriage ”,[1]这是关于匹配博弈理论的首次论述，揭示了婚姻市场和大学生招生市场两个现实的双方市场的稳定匹配状况，标志着匹配博弈理论的确立。2012年，哈佛大学教授埃尔文·罗斯(Alvin Roth)和洛杉矶加州大学教授罗伊德·夏普利(Lloyd Shapley)以在“稳定匹配理论和市场设计实践”方面的卓越贡献而获得诺贝尔经济学奖。匹配是市场的重要功能，匹配博弈理论的首要和核心工作是考证所研究的市场是否存在稳定匹配，换言之，匹配博弈理论运用博弈理论研究现实双方市场的稳定及因缺乏稳定而失灵的问题。[2]稳定匹配是匹配博弈理论寻求的最优结果。

稳定匹配是指匹配达到一种稳定的状态，当市场中的两个主体匹配达成时，他们都是匹配对象唯一的、不可调换的最终选择。双边匹配模型和延迟接受算法是稳定匹配理论的两块重要基石。[3]也就是说，达成稳定匹配需要完成两个步骤：第一步是建构双边匹配模型；第二步是采用延迟接受算法求解稳定匹配。市场的重要功能在于匹配，通过市场其中的主体和另一个主体相配对达成，比如，男女婚配、学校和学生之间的匹配等。“双边”的含义就是指市场中的两个集合体，并且第一集合的个体只能与第二集合个体相匹配。在具有双边市场的基础前提下，个体的偏好具有可靠性和实践性，而且市场没有任何限制，能够使任何匹配顺利达成，这样的匹配就是稳定的匹配。Gale和Shapley指出市场匹配稳定时必须具备两个条件：一是市场中两个不同类的个体在偏好上能够达成匹配；二是两个个体间的匹配形成后是不会被破坏的，不存在与另一类的其他个体再次进行匹配。双边匹配模型因为具有稳定匹配的性质，才使其理论得以推广。当前经济社会背景下，在诸多市场机制运行的实践活动中，通过一定的市场组织方式可以实现大多数个体间匹配达成，但是所形成的匹配缺乏稳定性。例如，20世纪50年代，美国内科医生的初级劳动力市场就存在着不稳定匹配的现象。[3]然而，应用双边匹配模型则可以消除匹配不稳定以及无序的问题。由此可以看出，双边匹配模型与其它组织形式所形成匹配的最大区别是双边匹配模型具有稳定匹配特征，是匹配的最佳模型。

除了双边匹配模型之外，稳定市场匹配理论的一个重要内容就是延迟接受算法。这一算法是Gale和Shapley研究学生申请学校和婚姻问题时提出的，也称为G-S算法。对于稳定市场匹配理论来说，延迟接受算法的主要任务就是对于双边匹配模型求解稳定匹配的结果。延迟接受算法是对市场中的两个主体A和B的个体进行稳定匹配的多回合计算。按照延迟接受算法的具体要求，整个计算过程如下：已知A={a1，a2，……，an}和B={b1，b2，……，bm}，并且主体A和B之间的存在着一定的偏好，这里用P(x)︱x=ai·bj来表示，例如，P(ai)=b2，b1，b5，……，bm，P(bj)=a1，a4，a2，……，an，这说明，个体ai对于主体B集合的选择顺序为b2，b1，b5，……；个体bj对于主体A集合的选择顺序为a1，a4，a2，……。求解稳定匹配的第一轮计算为：依据设定的偏好，主体A集合的ai个体向主体B集合的某一个个体bj发出匹配信息，此时，bj可能接受信息，也可能拒绝接受信息。当bj接受的信息数量超出其容量K时，bj就会拒绝向ai发出信息。对于bj的偏好函数P(bi)，ai是排在偏好最后的个体，此时剩余的偏好个体数量为W，并确保W≤K。求解稳定匹配的第二轮计算为：第一轮被拒绝的ai依据P(ai)中的第二偏好向主体B集合中的bj发出匹配信息，接下来仍然会发生bj的接受与拒绝。以此类推，直到不存在被拒绝的个体ai向bj发出匹配信息，那时匹配才算完结，稳定匹配可以达成。

面对真实生活中的配对问题，合理设计市场机制是实现稳定匹配效果的关键。罗斯(Alvin Roth)运用沙普利(Lloyd Shapley)的“延迟接受算法”和“最大交易圈子算法”基本理论，对市场失灵或缺失进行实践设计，有效地改善了市场绩效。并且形成了以市场设计理论为核心的一个新的经济学分支。市场失灵或者缺失通常表现出三种情形影响稳定匹配的效果：一是由于市场交易双方个体数量不足而使得市场规模的形成受到限制；二是由于市场交易双方个体数量过多而导致的交易双方缺乏足够的时间去实施偏好的有序进行；三是由于交易双方不愿意表达真实的偏好或者没有按照既定的偏好顺序进行匹配对象的选择而造成交易市场的虚假性。市场设计理论的核心思想就是通过设计合理的市场运行机制，进而解决或阻止上述三种市场失灵或者缺失的问题，即设计一个交易规则或者设立清算中心，[4]最终达到稳定匹配的效果。市场设计理论是对稳定匹配理论在实践中得以实施的条件与保障。稳定性和激励兼容是市场设计理论的主要特征。稳定性是指保证市场主体自愿参与市场交易所设计的市场规则。激励兼容则是指保证市场主体能够真实地表达偏好，阻止以策略性行为方式表达虚假偏好的设计规则。满足稳定性和激励兼容两个条件是采用沙普利延迟接受算法的首要问题。市场设计理论贡献体现在对沙普利算法的稳定性及激励兼容的证明中。[4]

3 马拉松赛事报名的双边匹配模型

3.1 模型的构建

在一个由m个马拉松赛事举办方和n个马拉松参赛者构成的马拉松赛事报名市场中，马拉松赛事举办方的构成用集合I={o1，o2，…，om}(m≥2)表示，每一个马拉松举办方具有一系列特征，例如办赛的经验与经历、办赛规模、知名度与影响力、赛事运营团队结构等，并且这些特征信息公开可知的。马拉松赛事参赛者的构成用集合J={c1，c2，…，cn}(n≥1000)表示，每个参赛者也具有一系列的特征，例如性别、年龄、职业、运动能力水平、参赛经历与经验等，这些特征信息体现在参赛者的网上报名系统中。马拉松参赛者为了获得马拉松参赛资格，需要得到马拉松赛事举办方的审批认可，从而双方达成一种办赛——参赛的关系。

假设一个马拉松赛事举办方可以允许众多参赛者参赛，而一个参赛者只能选择一个马拉松赛事进行参赛。实践表明，马拉松赛事一般审批通过成千上万个参赛者的参赛报名，建立参赛规模来扩大影响。然而，受到办赛经费状况、赛道地理条件、人力资源禀赋等限制，马拉松赛事的参赛人数是有明确的要求的。假设马拉松赛事举办方oi办赛的最多参赛人数为qi(qi≥1000)，qi称为马拉松赛事举办方oi的办赛容量。

参赛者通过网上报名系统向马拉松赛事举办方传达了参赛意愿信息，若其参赛意愿通过马拉松赛事举办方的审核认可而允许其参赛，则双方形成一种相互匹配的参赛关系。将这种参赛关系的集合命名为：H=I×J。马拉松赛事举办方与参赛者之间的匹配是一种双方对应选择关系的映射，这种映射记作μ，μ∈H。在这种映射关系中，与马拉松赛事举办方oi对应的参赛者用函数式表示为：μ(oi)=cj；与马拉松赛事参赛cj对应的举办方用函数式表示μ(cj)=oi。

在模型中，假设马拉松赛事举办方获取马拉松赛事的收益比例是固定的，都是λ(λ∈(0，1))，则参赛者分享的收益为1-λ。在这里，假设不存在转移支付，即不存在能力水平较差的参赛者为了获取赛事举办方的认可而承诺给予其更高的赛事收益。在达成办赛——参赛匹配关系之前，参赛者通过了解到的马拉松赛事举办方的特征形成参赛偏好，马拉松赛事举办方也根据网上报名系统中参赛者的信息构成办赛偏好。用匹配形成后马拉松赛事的事先价值V来表示这种偏好，这种事先价值就是匹配价值。V的大小取决于马拉松赛事举办方和参赛方双边偏好的结合。马拉松赛事举办方oi给予参赛者cj参赛资格的马拉松比赛的价值Vij。假如马拉松赛事举办方没有与任何参赛的另一方匹配，那么，其匹配价值就等于0。通常情况下，马拉松赛事举办方与参赛方的偏好是严格的。不同匹配所形成的“办赛——参赛”共同体的价值是不相同的，即Vij=Vij或Vij=Vij是不存在的。若Vij>Vij，表示相对于马拉松赛事举办方oi，举办方oi更愿意与马拉松赛事参赛者cj相匹配；若Vij>Vij，则表示相对于马拉松赛事参赛者cj，参赛者cj更愿意与马拉松赛事举办方oi相匹配。

马拉松赛事举办方oi和参赛者cj的效用函数分别记作Ui(μ(i))和uj，进而得出：

Uj〈μ(j)〉=(1-λ)Vμ(j)j

马拉松赛事举办方与参赛方的双边匹配博弈主要是解决双方效用最大化的问题，模型的构建分别为：

S.T.:maxUi(μ〈i〉)=(1-λ)Vμ(j)j

3.2 模型的均衡

马拉松赛事举办方与参赛方双边匹配博弈的均衡就是要使匹配博弈的双方达成稳定的状态，即形成稳定的双边匹配博弈。也就是说，当所有马拉松赛事举办方和参赛者都不愿意放弃已达成的匹配而去选择新的匹配时，这样的匹配状态就是稳定的匹配。双边匹配博弈的稳定状态是非常严格的。马拉松赛事举办方与参赛者之间的匹配关系oj∈μ(i)是不存在的。这种不可能成立的匹配关系表现为以下两种情形：首先，相对于oi来说，cj更愿意选择oi作为匹配对象，并且oi有充足的参赛名额；其次，相对于cj来说，oi更愿意选择cj作为匹配对象，并且cj尚未得到其他马拉松赛事举办方给与的参赛资格。

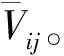
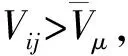
4 马拉松赛事双边匹配模型的求解及其应用

4.1 模型的求解

Gale和Shapley对于双边匹配博弈提出了采用“延迟接受”算法来求解模型的均衡。对于本文所研究的马拉松赛事主办方和参赛者双边匹配博弈模型，“延迟接受”算法同样适用。根据“延迟接受”算法的逻辑思想要求，马拉松赛事参赛者通过分析与不同马拉松赛事举办方形成匹配所表现出来的马拉松比赛匹配价值，进而对马拉松赛事举办方进行排序。马拉松赛事参赛者首先向排序最前(马拉松比赛举办方与参赛者匹配价值最大)的马拉松赛事举办方传递参赛意愿信息。马拉松赛事举办方接收到参赛意愿信息后，根据其马拉松比赛匹配价值排序，按照马拉松赛事所设置的参赛人数容量q的要求，选择确定q个马拉松赛事参赛者的参赛资格，q之后的参赛者将处于落选的状态。如果马拉松赛事举办方设置的参赛人数容量q大于马拉松赛事参赛者的报名人数，那么所有马拉松赛事参赛者都将获得参赛资格。

对于第一轮配对未达成的参赛者按要求将继续向排序次优的马拉松赛事举办方(其他马拉松赛事)传递参赛意愿信息，以此方式进一步完成配对的策略目标。此时，马拉松赛事举办方将会依据参赛者参加马拉松赛事的匹配价值(参赛者条件、能力水平等方面的综合评价)和马拉松赛事设置的参赛容量的剩余状况，择优选择达标的参赛者，而放弃未达标的参赛者。

依照上述方式继续进行匹配，直到达成“报名——接受”的参赛匹配为止。也就是说，未被认定参赛资格的马拉松赛事参赛者依照马拉松参赛匹配价值的排序，依次向马拉松赛事举办方传递参赛信息，当其中任意一个举办方接纳时，双边配对过程就此结束；马拉松赛事举办方则以马拉松参赛匹配价值和参赛容量为依据，确定接纳参赛价值排序居前的参赛者的参赛资格，直到达到设置的参赛人数容量为止。

由此可见，当马拉松赛事参赛者的参赛意愿信息被其中一个马拉松赛事举办方确定认可，且当马拉松赛事举办方所设置的参赛人数容量全部配发完结时，马拉松赛事参赛者与举办方的双边匹配博弈完成。此时，马拉松赛事的参与与举办的匹配模型是一个稳定的结构。

4.2 模型的应用

我们将马拉松赛事市场设定为：6个马拉松赛事参赛者I={o1，o2，o3，o4，o5，o6}和4个马拉松赛事举办方J={c1，c2，c3，c4}，也就是说，6个参赛者希望获得4个马拉松赛事举办方的参赛许可。假设马拉松赛事举办方的接受容量为2、2、1、1。马拉松赛事举办方和参赛者的价值表1所示。

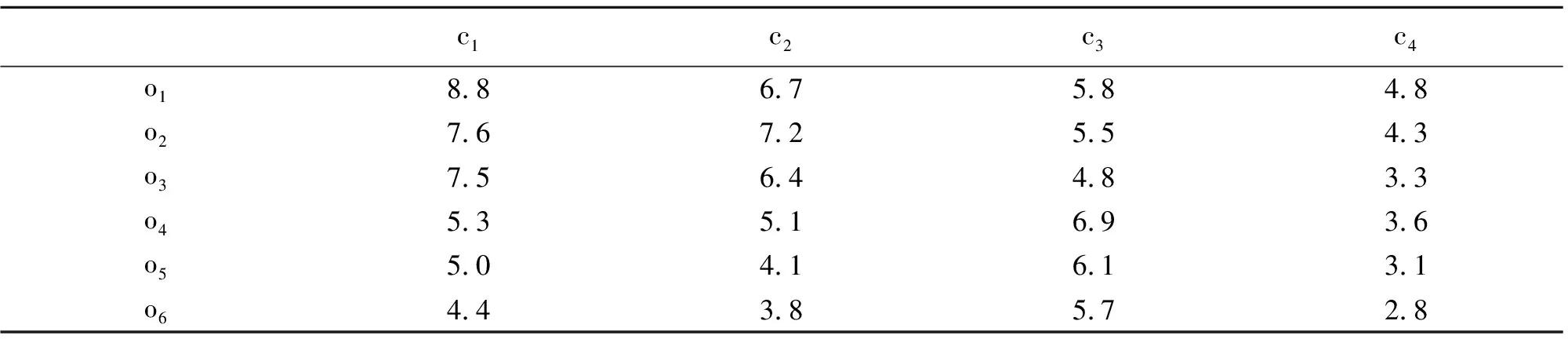
表1 马拉松赛事举办方和参赛者的匹配价值

通过对表1中马拉松赛事举办方与参赛者匹配价值大小的比较，可以分析出双方匹配的全过程。

首先是第一轮，马拉松赛事参赛者o1、o2、o3都向他们最偏好的马拉松赛事的举办方c1发送了报名参赛的资料信息，o4、o5、o6则都向他们最偏好的马拉松赛事的举办方c3发送了报名参赛的资料信息，赛事举办方c2和c4却没有接收到参赛者的资料信息。收到报名资料信息的赛事举办方们根据匹配价值选择适于参赛的马拉松赛事报名者。于是，产生这样的结果：马拉松赛事参赛者o1、o2被举办方c1准许参赛，参赛者o4被举办方c3准许参赛。然而，参赛者o3、o5、o6的报名资料信息却没有被其他马拉松赛事举办方们所认可通过。此时，匹配的首轮次结束，马拉松赛事举办方c2和c4的许可参赛容量为2和1。

其次是第二轮，马拉松参赛者o3、o5、o6分别向各自次优偏好的赛事举办方递交参赛报名资料信息。根据马拉松赛事举办方的参赛容量要求，此时的赛事举办方c1和c3已经没有参赛容量，因而，c1和c3拒绝参赛者o3、o5、o6的参赛报名请求。就有举办方c2和c4可以接收参赛者的报名请求，根据匹配数值的大小，仅有c2接收了o3和o5的参赛报名请求，参赛者o6的参赛报名请求再次被拒绝。此阶段，只有赛事举办方c4还剩有1个参赛容量。

再次是第三轮，参赛者c4向第三偏好的赛事举办方报名参赛，但由于c1、c2、c3均用尽了各自的参赛容量，因而，o6只能向c4递交参赛请求，c4递接受了o6的参赛报名请求。

至此，马拉松赛事参赛者与举办方的双边匹配结束，一个稳定的匹配就此形成，其结果表示为：

5 结论

马拉松赛事报名参赛问题表现突出，已经成为该项赛事良性发展的瓶颈。本文运用双边匹配博弈模型，分析了马拉松赛事举办方和参赛者双向选择的参赛关系，阐释了达成自身效用最优化的问题。通过研究认为，马拉松赛事举办与参赛的博弈模型中，所构成的均衡是唯一、稳定的。对于稳定均衡下的举办方与参赛者的选择都是满足各自偏好的，且是最优的。同时，在该模型中，所形成的匹配对数量等于马拉松赛事举办方设置的参赛容量。

马拉松赛事举办与参赛的双边匹配博弈模式的构建对于马拉松赛事举办参赛市场的设计具有重要的指导意义和推广转化启示作用。首先，双边匹配博弈是完全信息的博弈，所形成的最优、稳定匹配的前提必要条件是信息是完全的，匹配双方的所有信息都能够被观察到和查询出来的。所以，将马拉松赛事参赛者的参赛资料信息科学管理，使其公开、易被查询了解，同时，加强马拉松赛事参赛资格认定市场的公平与透明程度。这些都将会加强与完善马拉松赛事参赛市场的有效性起到关键的作用。其次，在双边匹配博弈模型中，稳定状态下所形成匹配对的数量是影响马拉松赛事举办方进入市场的重要因素。但是在我国，真正有效的配对数目有非常有限的。因而，只有配对数目与举办方设定的参赛容量相互吻合时，马拉松赛事举办方进入市场才是具有经济效率的。再次，在马拉松赛事双边匹配模型中，稳定的匹配要求举办方对于参赛者的参赛特征具有较为一致的偏好，所以，不同的参赛者都会受到更多的不同举办方的认可。