不同开挖顺序下软土深基坑受力与变形对比分析

2019-07-16吴新宇彭海燕

工程质量 2019年6期

刘伟，吴新宇，彭海燕

（1.中交路桥华南工程有限公司，广东中山 528400；2.长安大学公路学院，陕西西安 710064；3.中国建筑科学研究院有限公司，北京 100013）

0 引言

近年来，各大城市竞相发展地铁交通，地铁车站深基坑作为一项重点控制性工程，由于其施工风险高、施工难度大等特点，受到各界高度关注。

一直以来，国内外学者对深基坑的研究高度重视，并取得了丰硕成果。早在 20 世纪 30年代，Peck［1］与Terzighi［2］依据基坑土体变形与支撑轴力之间的关系，提出了总应力法的理论，经过之后不断修正，该理论发展成受大家认可的基坑变形基本理论，沿用至今。Mana［3］对相同开挖支护形式下的基坑抗隆起系数与地下连续墙最大侧向位移之间的关系进行分析，提出用于计算周边地表最大沉降值与围护结构侧向变形的稳定安全系数法。陈永福等［4］分析了上海地区软黏土在加载-卸荷过程中对应的土体应力-应变关系，提出了估算全补偿沉降值和土体回弹量的计算公式。

为分析不同开挖顺序下，对基坑施工周边环境的影响及其围护结构的受力特征，本文依托佛山市地铁三号线大良站深基坑工程，对深基坑在两端向中间开挖与中间向两端开挖两种开挖顺序下的基坑变形和围护结构受力情况进行建模计算，对计算结果进行分析比较，提出分段分层开挖顺序的优化方案。为今后同类工程深基坑开挖方案选择提供参考，具有一定的价值和实际意义。

1 工程概况

佛山市地铁三号线大良站总长度为 266 m，标准段宽度为 19.9 m，开挖深度为 25.3 m，标准段顶板覆盖土层厚 3.52 m，基坑安全等级为一级。车站主体围护结构采用地下连续墙，墙身厚度为 0.8 m，深度为 29～33 m，标准段内支撑采用径向 4 道支撑，第一道“米”字撑为700 mm×900 mm 的钢筋混凝土撑，水平间距为 9 m，第二、三、四道为φ609 双拼钢管支撑，水平间距为 4.5 m。基坑现场如图1 所示。

图1 基坑现场图

本车站微地貌属剥蚀残丘与冲洪积平原交接地带，车站西侧为缓坡，南侧、东侧为山前冲洪积平原，地形总体西高东低；该基坑地层自上而下分别为素填土、粉质黏土、全风化泥质砂岩与强风化粉砂岩。基坑土层分布如图2 所示。由图2 可看出，基坑大里程端，靠近“刀把口”段，全风化泥质砂岩层较厚，与两端相比，该段土质相对较软。

图2 基坑土层分布

2 模型建立及相关参数选取

2.1 模型尺寸及网格划分

基坑模型的尺寸距离基坑四个边界约为 2 倍的基坑开挖深度，模型底部边界至地面距离约为 2 倍的基坑开挖深度。大良站基坑长度为 266 m、全段最大宽度为 25 m，基坑开挖深度为 25.3 m，故模型尺寸为 366 m× 125 m×60 m（X×Y×Z）。

在本章中对基坑几何模型采用 MIDAS GTS NX 中的网格自动划分功能，以 3.5 m 为控制尺寸通过混合网格生成器对基坑模型土体进行自动网格划分。最终模型共划分为 111 778 个单元和 53 730 个节点，模型尺寸及网格单元划分示意图如图3 所示。

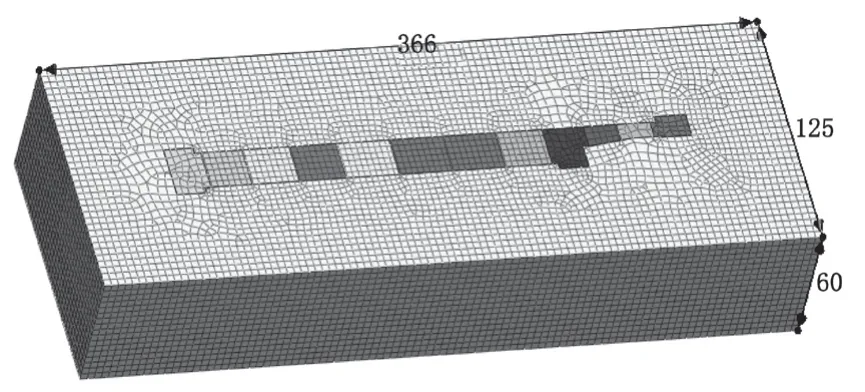
图3 模型尺寸及网格单元划分示意图（单位：m）

2.2 地层划分及参数选择

为更接近现场实际地层分布，考虑基坑纵向上不同断面处土质的不同，基坑模型的地层划分在实际基坑土层分布的基础上进行了适当简化，忽略分布厚度较薄的土层，将参数相近的土层进行了合并，即在基坑纵向的不同断面处，其地层分布情况均不同。各层土的具体参数如表1 所示，围护结构参数如表2 所示。

2.3 边界条件确定

根据基坑变形理论与大量工程实例可知，当超出基坑开挖影响区后，变形大幅减小，可忽略不计。故把模型边界土体看作不动边界，使用 MIDAS GTS NX 中静力/边坡分析中的约束功能，对模型底部边界设置竖直向下位移约束，对模型四周边界设置向远离基坑方向的位移约束，不对模型上表面进行约束，使模型上表面为自由面。

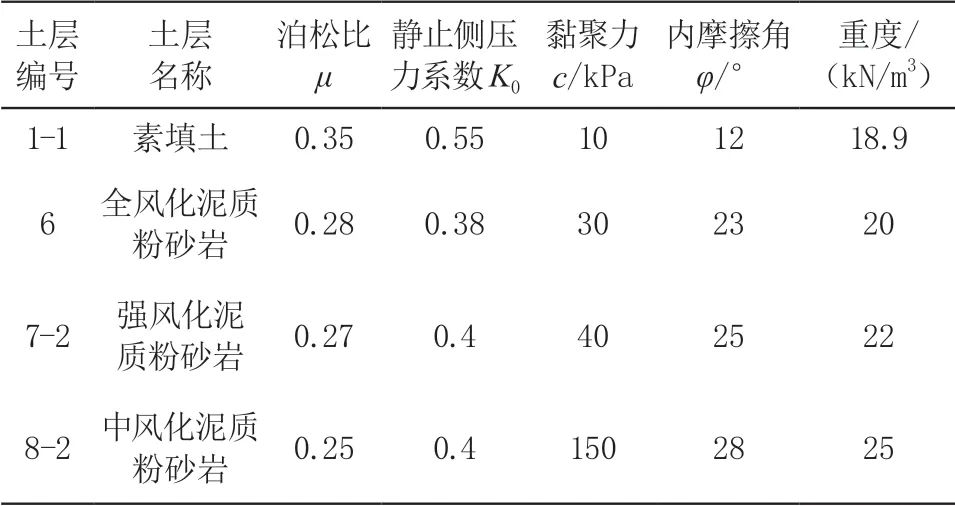
表1 土体物理参数表

表2 基坑围护结构相关参数

2.4 开挖顺序设置

深基坑开挖采用常见的分段分层开挖法，本文分别对基坑两端向中间开挖和基坑中间向两端开挖这两种开挖顺序进行模拟计算。基坑纵剖面开挖示意图如图 4 所示。

图4 基坑纵剖面开挖示意图

3 两种开挖顺序下计算结果对比分析

本文选取 4 个代表性断面进行分析，分别为断面1～断面 4，如图5 所示。

图5 分析断面平面布置图

3.1 墙体水平位移对比分析

两种开挖顺序引起的各断面墙体水平位移量如表3 所示。断面 1 和断面 3 的墙体水平位移曲线图如图6、图7 所示（限于篇幅有限，本文仅选取具有代表性的断面）。

表3 各断面墙体水平位移量 mm

从图6、图7 可以看出，两种开挖顺序下，墙体水平位移曲线形态均属于中间大两端小的抛物线形曲线。各断面墙体水平位移随着下一步关键施工节点的完成而增大，即开挖越深，墙体水平位移曲线的“腹部”越凸出，最大位移点向更深处移动。

通过对墙体水平位移模拟计算结果进行比较，两种开挖顺序下，最大墙体水平位移量均呈现断面 3＞断面 4＞断面 2＞断面 1 的位移变形规律。4 个断面在两种开挖顺序下的最大墙体水平位移量相差较小，其中最大水平位移差值出现在断面 3 右侧，由基坑两端向中间开挖比由基坑中间向两端开挖的最大水平位移量大 2 mm；其次为断面 4 右侧的位移差为 1 mm，其余断面位移差均小于 1 mm。断面 3 墙体水平位移量最大的原因在于，该断面处于基坑平面中部，受到边角效应影响最小，且该断面所处地层土质与断面 1、2 相比较差。断面 1 墙体水平位移量最小的原因在于，该断面处于基坑平面端头，受到的边角效应影响很大，左右两侧墙体在地连墙南端短边的协同受力下，抗变形能力最大，且该断面所处地质与断面 3、4 相比较好。

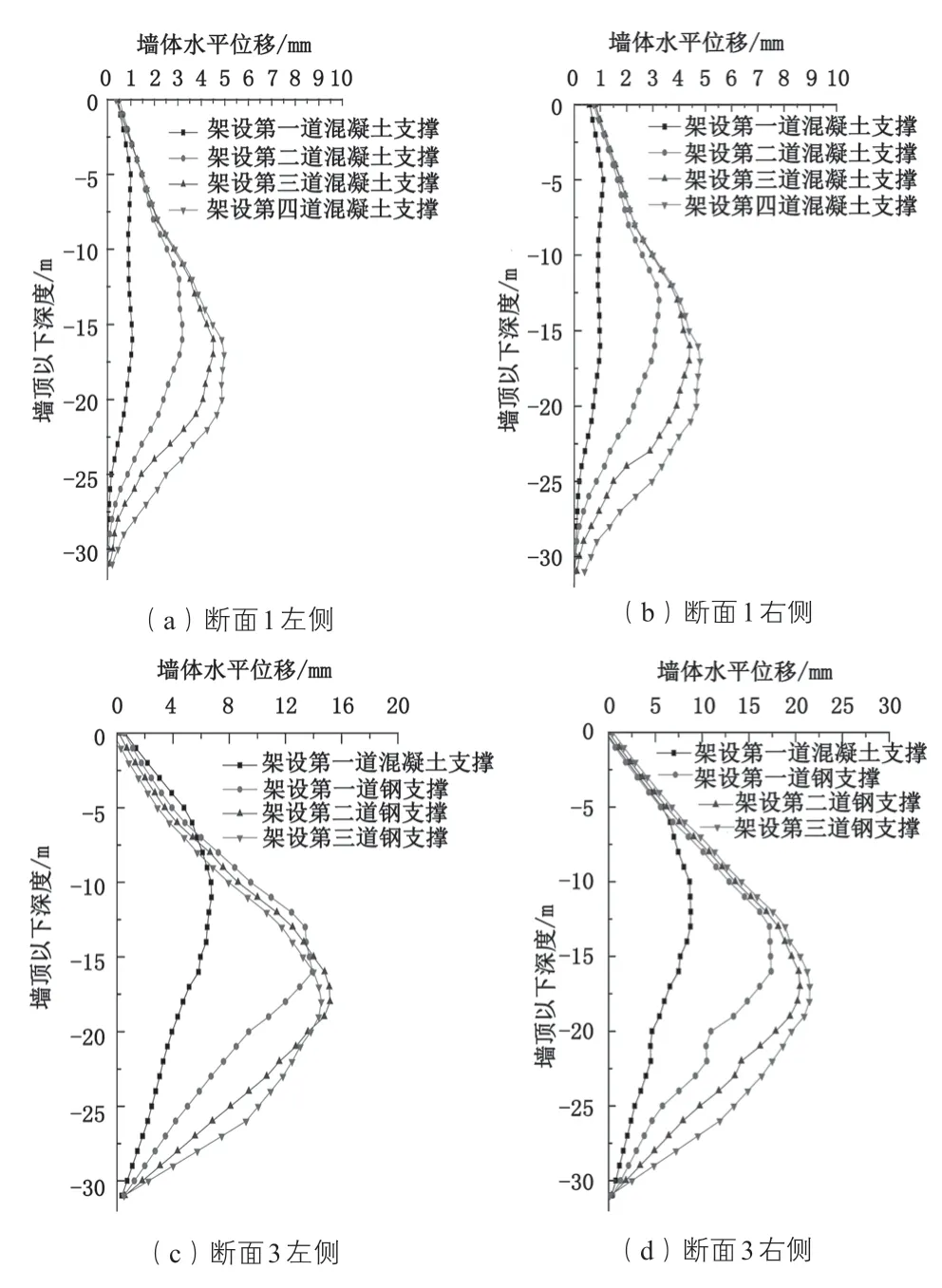
图6 两端向中间开挖引起的墙体水平位移曲线图

图7 中间向两端开挖引起的墙体水平位移曲线图

在地铁深基坑工程中，由于基坑普遍处在周边环境复杂的市区中，对基坑施工中引起的围护结构变形控制要求较高，监测规范中对墙体水平位移量的控制值一般为 30 mm，故虽然经模拟计算后得到两种开挖顺序下的最大墙体水平位移差值仅为 2 mm，但在地铁深基坑工程中也不可忽视其对基坑安全的影响。本次对两种开挖顺序下墙体水平位移的计算结果说明了在严格按照“分段开挖、及时支撑”的原则进行模拟计算下，由基坑两端向中间的顺序开挖与由基坑中间向两端的顺序开挖造成的墙体水平位移量相差较小。

3.2 周边地表沉降对比分析

两种开挖顺序引起的各断面周边地面沉降量如表4 所示。断面 3 和断面 2 的地表沉降曲线图如图8、图9 所示（限于篇幅有限，本文仅选取具有代表性的断面）。

表4 各断面周边地表沉降值mm

从图8、图9 可以看出，两种开挖顺序下，周边地表沉降曲线变化均为沉降量随基坑开挖加深而增大，距离基坑边缘远近不同其地表沉降量也不同，地表沉降曲线由距基坑近处至远处总体呈现出开口朝上的“勺型”或抛物线型变化，且随着开挖加深曲线“凹陷”越明显。

通过对周边地表沉降模拟计算结果进行比较，两种开挖顺序下，周边地表沉降量均呈现断面 3 沉降最大，断面 2 沉降量次之，断面 1 与断面 4 的沉降量稍有差异但大体相近。4 个断面在两种开挖顺序下的沉降差均较小，最大沉降差出现在断面 3 左侧，由基坑中间向两端开挖的最大沉降量比由基坑两端向中间开挖的最大沉降量大 0.42 mm；其次为断面 3 右侧的最大沉降差值为 0.25 mm，其余断面在两种开挖顺序下产生的最大沉降差均小于 0.2 mm。

图8 两端向中间开挖引起的周边地表沉降曲线图

值得一提的是，模拟计算结果各断面的最大沉降点出现在距基坑边缘 10～15 m 处，即 0.4 H～0.6 H（H 为基坑开挖深度），但现场监测结果的最大沉降点分布范围在 0.2 H～0.4 H 处。模拟计算结果与实际监测结果存在一定差别，造成此差别原因为现场地质复杂、施工因素众多，基坑模型无法完美模拟出现场各方面条件，但沉降曲线变化形态相近，该误差属于合理现象。此外，模拟计算结果中周边地表沉降量呈现出在基坑两端较小，中部较大的规律，与现场监测得到的周边地表沉降规律一致。

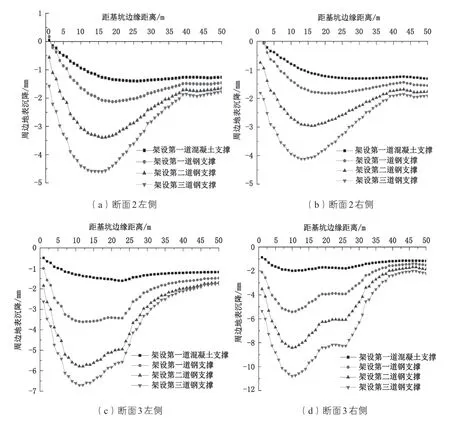
图9 中间向两端开挖引起的地表沉降曲线图

由于城市中高层建筑物分布密集，众多地下管线错综复杂地埋设于地下，在一定条件下较小的地表不均匀沉降量便能使建筑物开裂甚至倾斜，使刚性地下管线受剪折断而出现安全隐患。因此，在城市中进行深基坑开挖施工对地表沉降的控制要求非常严格，根据监测规范中规定地表沉降控制值为 25 mm。本次对两种开挖顺序下周边地表沉降的模拟计算得到的 4 个断面中最大沉降差值为 0.42 mm，说明在严格按照“分段开挖、及时支撑”的原则进行开挖围护施工的模拟计算下，由基坑两端向中间开挖与由基坑中间向两端开挖造成的基坑周边地表沉降值相差不大。

3.3 墙体弯矩对比分析

两种开挖顺序引起的各断面各段面墙体弯矩值如表5 所示。各断面墙体弯矩曲线图如图10、图11 所示。

表5 各断面墙体弯矩值 mm

由图10、图11 可看出，两端向中间开挖时，4 个断面的墙体弯矩范围在 -400～800 kN·m 之间；中间向两端开挖时，4 个断面的墙体弯矩范围在 -400～700 kN·m 之间；弯矩曲线分布形态近似呈关于基坑中线轴对称分布。

通过对比 4 个断面的墙体弯矩最大值，发现断面 1、断面 2、断面 4 在开挖全过程中的左右两侧墙体弯矩最大值均出现在最后一个施工节点，即四道支撑架设完成并开挖至基底，而断面 3 在开挖全程的墙体弯矩最大值出现在第二个施工节点，即架设第二道支撑并挖除第二层土体时；另外，对比分析 4 个断面在最后一个施工节点即架设第四道支撑并开挖至基底时的最大墙体弯矩点所处深度，可看出断面 2 与断面 4 的最大弯矩点在地面以下 26 m 处，而断面 1 在开挖至基底时的最大弯矩点深度为地面以下 20 m 处，断面 3 的最大弯矩点出现在地面以下 18 m 处。

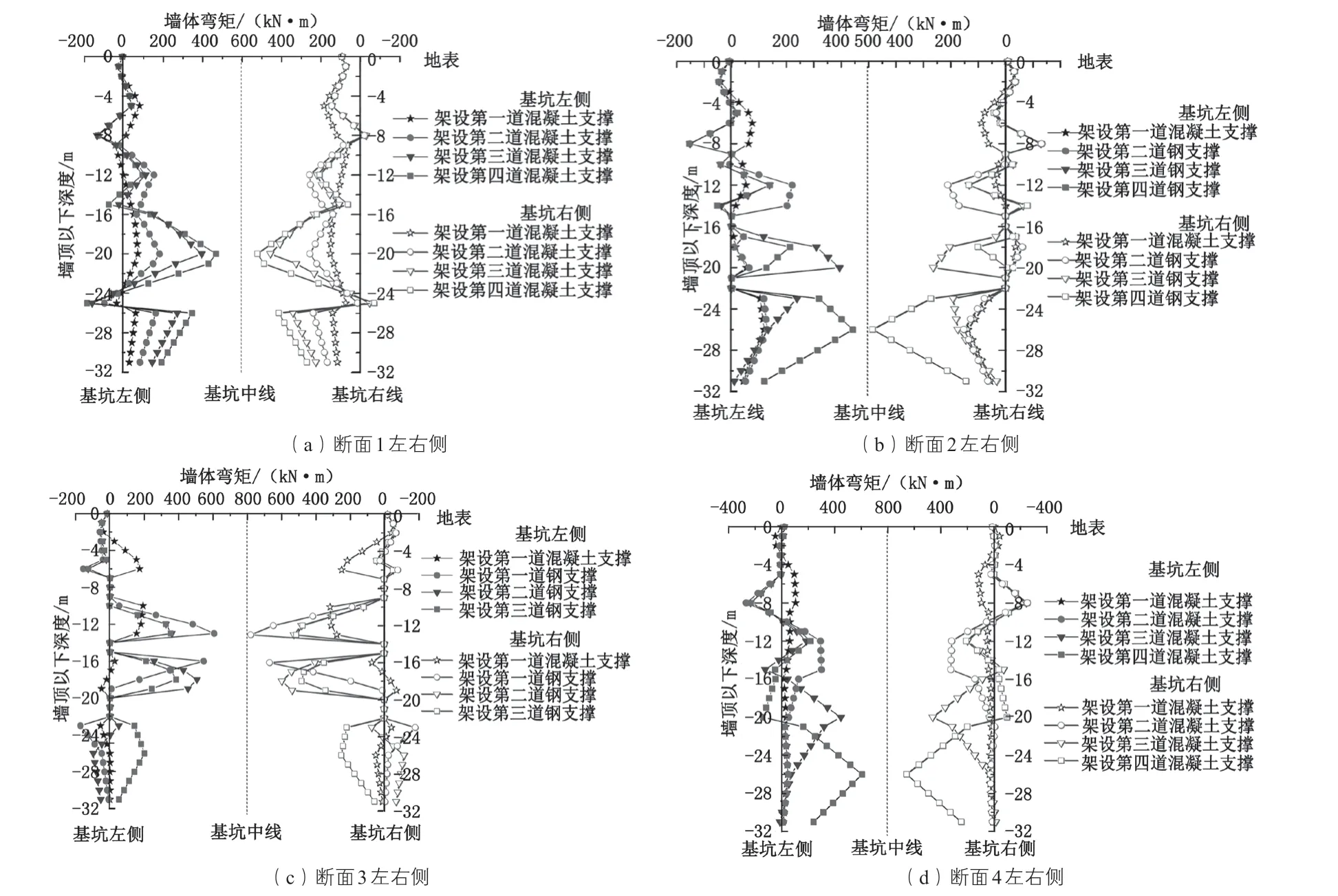
图10 两端向中间开挖时墙体弯矩曲线图

图11 中间向两端开挖时墙体弯矩曲线图

对图10（a）与 11（a）比较可知，断面 1 两侧除了在深度为 24 m、25 m 处的弯矩差为正值外，其余深度范围的弯矩差均为负值，即由基坑两端向中间开挖的墙体弯矩均小于由基坑中间向两端开挖的墙体弯矩，最大弯矩差出现在架设第一道支撑时地面以下 20 m 深度处，断面 1 左右两侧的最大弯矩差绝对值分别为 37.4 kN·m 与 35.6 kN·m，随着开挖继续，弯矩差渐渐减小至 20 kN·m 以下。

对图10（b）与 11（b）比较可知，断面 2 两侧在全深度范围内的弯矩差除了在个别深度为负值，其余深度范围的弯矩差均为正值，即由基坑两端向中间开挖的墙体弯矩均大于由基坑中间向两端开挖的墙体弯矩，最大弯矩差出现在架设第二道钢支撑时地面以下 20 m 深度处，且断面 2 左右两侧的最大弯矩差绝对值分别为 146.8 kN·m 与 126.2 kN·m。

对图10（c）与 11（c）比较可知，在断面 3 两侧全深度范围内的弯矩差值有正有负，左侧的最大正弯矩差值为架设第一道钢支撑时地面以下 16 m 深度处的 289.2 kN·m，最大负弯矩差值为架设第二道钢支撑时地面以下 16 m 深度处的 -197.5 kN·m；右侧的最大正弯矩差值为架设第一道钢支撑时地面以下 16 m 深度处的321.65 kN·m，最大负弯矩差值为架设第二道钢支撑时地面以下 16 m 深度处的 -186.42 kN·m。

对图10（d）与 11（d）比较可知，在断面 4 两侧全深度范围内的弯矩差值有正有负，左侧的最大正弯矩差值为架设第一道混凝土支撑时地面以下 1 m 深度处的29.52 kN·m，最大负弯矩差值为架设第四道混凝土支撑时地面以下 20 m 深度处的 -75.64 kN·m；右侧的最大正弯矩差值为架设第一道钢支撑时地面以下 1 m 深度处的 31.32 kN·m，最大负弯矩差值为架设第二道钢支撑时地面以下 20 m 深度处的 -60.8 kN·m。

以上对 4 个断面的两种对比结果说明围护墙体在开挖过程中受力情况复杂，围护墙体并非都是在开挖至基底时出现最大弯矩，最大弯矩点也并非都是在基底处。故对墙体弯矩进行分析时，应将各施工节点的各段深度处弯矩极大值都纳入考虑范围，才能全面了解开挖过程中围护墙体受力情况并及时采取相关措施进行控制，防止墙体弯矩过大发生结构失稳破坏。