基于时间序列分析的房屋安全监测数据处理研究
2019-07-16韩晓健
韩晓健,徐 翌
(南京工业大学,江苏 南京 210000)
0 引 言
房屋的安全状况直接关系到人民群众的生命财产安全[1]。20 世纪建造的房屋由于年久失修以及在使用过程中遭受的自然灾害和人为破坏,使房屋安全性逐年降低,甚至发生破坏倒塌事件。例如在 2017年2月2日,温州市文成县 4 间民房坍塌,造成 7 人死亡 2 人受伤。惨痛的教训表明,对老旧房屋进行动态监测,保障结构在使用过程中的安全性,防止意外事故的发生,是一项非常重要的工作。
房屋安全监测系统克服了传统人工检测成本高、效率低、受检测人员经验水平限制等缺点,它利用物联网技术,通过仪器对房屋进行实时监测预警,掌握结构的变形和构件安全状态,及时发现结构存在的安全隐患,以便采取应急措施,保障建筑结构的安全使用,避免人员与财产的损失[2]。
监测系统采集的数据受到噪声干扰、设备故障等因素的影响,会使原始数据存在异常和噪声。而且大多数的监测系统只是把原始数据简单地呈现在界面上,观察数据的变化趋势以及是否报警。这样使得大量的监测数据得不到妥善的处理与利用,难以发现监测数据中有规律的、重要的信息,导致了数据资源的巨大浪费,不利于结构的状况评估和安全预警,甚至可能导致错误的分析结果[3-4]。因此,对监测数据进行处理和分析是至关重要的。
1 监测数据预处理方法
监测数据经过预处理后,能够剔除异常数据,填补缺失数据,获得真实的数据,并将数据进行转化,进而提高数据挖掘的质量。本文主要介绍了对监测数据异常值、缺失值和数据平滑处理的方法。
1.1 异常值处理
异常值是指样本中的个别值明显偏离其它的观测值[5]。
本文采用箱型图进行异常值剔除。箱形图对数据不作任何限制性要求,能够直观地反映数据的分布,是一种比较简单、有效的判断异常值的方法。它提供了识别异常值的一个标准。
异常值<QL-1.5 IQR 或异常值>QU+1.5 IQR
其中 QL 称为下四分位数,表示全部观察值中有四分之一的数据值比它小;QU 称为上四分位数,表示有四分之一的数据值比它大;IQR 是四分位数间距,是 QU 与 QL 之差。图1、2 是采用箱型图剔除异常值的结果。
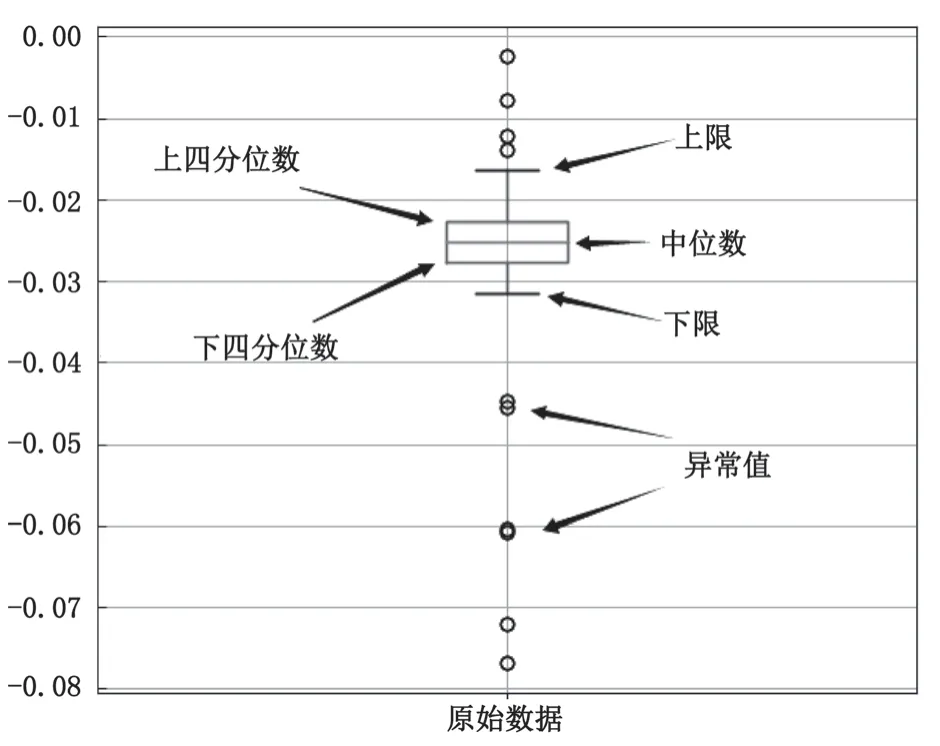
图1 箱型图
少量的异常值可以直接删除,或者视为缺失值进行插补处理。如果监测数据中出现了大量的、连续的异常值,则需要分析这些异常值产生的原因,这才是解决异常值的根本[6]。

图2 剔除异常值前后对比曲线
1.2 缺失值处理
监测设备由于故障、停电等原因也会产生缺失值。数据缺失会对数据处理的结果造成误差,给数据分析带来一定的麻烦。下面给出了插补缺失数据的常用方法。
1)最近邻插补。利用与缺失值最接近的数据值代替。
2)回归方法。根据已有数据建立拟合模型来预测缺失值。
3)插值法。利用已知点建立合适的差值函数 f(x),缺失值由其相对应的 xi求出的函数值 f(xi)来近似 代替。
本文采用拉格朗日插值法对缺失数据进行插补。已知 n 个点坐标(x1,y1),(x2,y2),…,(xn,yn),则可构造拉格朗日插值多项式,如式(1)所示。

然后将缺失值对应的横坐标 xi代入插值多项式,即可得到缺失值的近似值 L(xi)。对上文剔除异常值后的数据进行拉格朗日插值,如图3 所示。
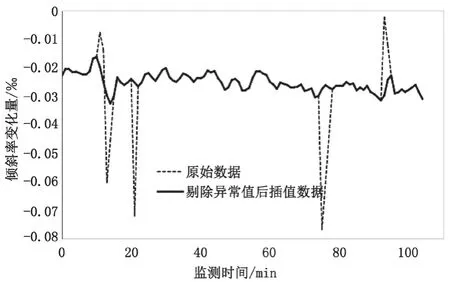
图3 拉格朗日插值处理后曲线
1.3 数据平滑处理
监测系统采集的数据通常是真实值和各种干扰或噪声等成分迭加在一起的结果。为了消除噪声成分而让真实值保留下来,需要对原始数据进行平滑处理。常用的数据平滑方法有移动平均法、中值滤波等。
本文采用移动平均方法,平滑效果如图4 所示。它的基本思想是对监测数据依次计算包含一定项数的平均值,逐项推移,可以消除随机波动和季节性的影响,得到序列的变化趋势。
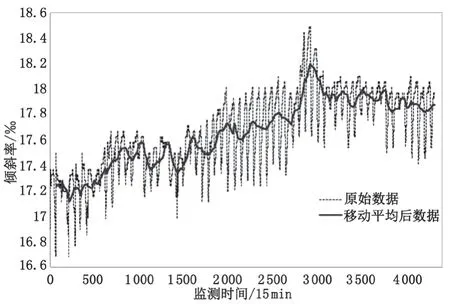
图4 移动平均法处理后对比曲线
2 监测数据的分析预测
时间序列通常是指按时间顺序排列的一系列观测数据,监测系统所采集的数据正符合时间序列的定义。将时间序列分析方法应用到房屋安全监测中,分析监测数据的变化特征和趋势,预测数据未来的发展,帮助管养单位防范危险的发生。
2.1 时间序列模型[7]
设序列{xt}为平稳、正态、零均值的时间序列,在 t 时刻的随机变量 xt是前 p 期 xt-1,xt-2,…,xt-p和前 q 期的随机扰动 εt-1,εt-2,…,εt-p的多元线性函数,得到自回归移动平均模型,记为 ARMA(p,q)模型如式(2)所示。
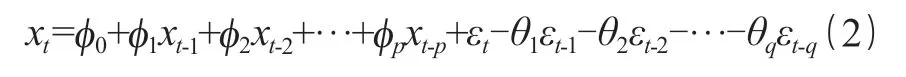
式中:p 为模型的自回归阶数;q 为移动平均阶数;φ、θ 为不为零的待定系数;{εt}为零均值的随机干扰项。
特别的,当 q=0 时,ARMA(p,q)模型就变为 p 阶自回归模型,记为 AR(p),如式(3)所示。
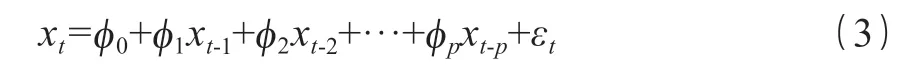
当 p=0 时,ARMA(p,q)模型就变为 q 阶移动平均模型,记为 MA(q),如式(4)所示。
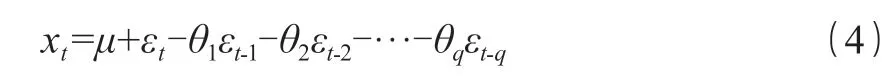
2.2 建模的一般步骤
1)平稳性检验。可以根据原始数据的时序图、自相关函数或者通过单位根(ADF)检验,对序列的平稳性进行识别。如果序列非平稳,可以使用差分的方法对数据进行差分处理,实现序列的平稳化。
2)白噪声检验。为了确定序列是否有分析的价值,需要进行白噪声检验。一般是构造检验统计量来检验序列的纯随机性,例如 Q 统计量、QLB统计量。
3)模型识别。对平稳非白噪声序列的自相关系数和偏自相关系数进行分析,判断其拖尾性和截尾性,确定模型的类别和阶次,定阶原则如表1 所示。

表1 模型定阶的基本原则
4)参数估计。确定拟合模型后,求出模型中的未知参数的值。常用的参数估计方法有极大似然估计和最小二乘估计等。
5)模型检验。判断模型残差是否为白噪声,如果残差是非白噪声,说明残差中还存在可以提取的有用信息,此时需要对模型进一步改进。
6)模型优化。如果一个序列能构造多个显著有效的模型,可以通过最小信息准则从中选择最优模型。
7)模型预测。利用最终建立好的模型对序列未来的发展进行预测。
3 工程实例
3.1 工程概况
某居民楼建于 20 世纪 90年代,7 层砌体结构,材料强度不符合设计要求,各层承重墙体被普遍违规拆改,房屋地基不稳定、倾斜严重。根据现场倾斜测量结果:最大倾斜率为偏东 17.2 ‰。
本次监测采用基于云平台的房屋安全监测系统对该居民楼倾斜情况进行实时监测。在楼顶东西两边各安装一个倾角传感器 Q 1、Q 2,传感器测点布置如图5 所示。X 方向的监测方向为东西向;Y 方向的监测方向为南北向。

图5 倾角传感器安装位置示意图
3.2 模型建立
以测点 Q2 为例,取 2018年9月1日至 10月31日,共 61 期监测数据,对前 55 期数据进行建模分析,后 6 期数据作为预测结果的比较。
图6 的数据是经过预处理后的房屋倾斜数据,直观地发现该数据有明显的增长趋势,初步判断该序列是非平稳、非白噪声的时间序列。
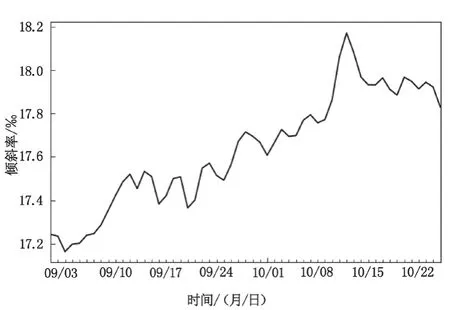
图6 原始序列图
对原始序列进行一阶差分运算使其平稳化,差分公式为:Δxt=xt-xt-1。一阶差分后序列{Δxt}的时序图如图7 所示,差分序列基本上消除了趋势项。采用 ADF 检验的方法判断差分序列平稳性,求得 τ 统计量对应的 P 值为 1.85×10-11,远小于给定的显著性水平 α=0.05,属于平稳序列。
然后对差分序列{Δxt}进行时间序列分析。由图8 可以看出,差分后数据的自相关系数和偏自相关系数在二阶延迟后均在2倍标准差以内,呈现出明显的二阶截尾现象。为了尽量避免因个人经验不足而导致的模型识别不准,本文尝试了建立 ARMA(2,0)、ARMA(2,1)和ARMA(2,1)模型,然后再根据最小信息准则选择最优模型。
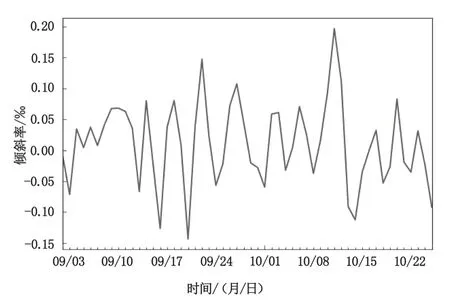
图7 一阶差分数据图
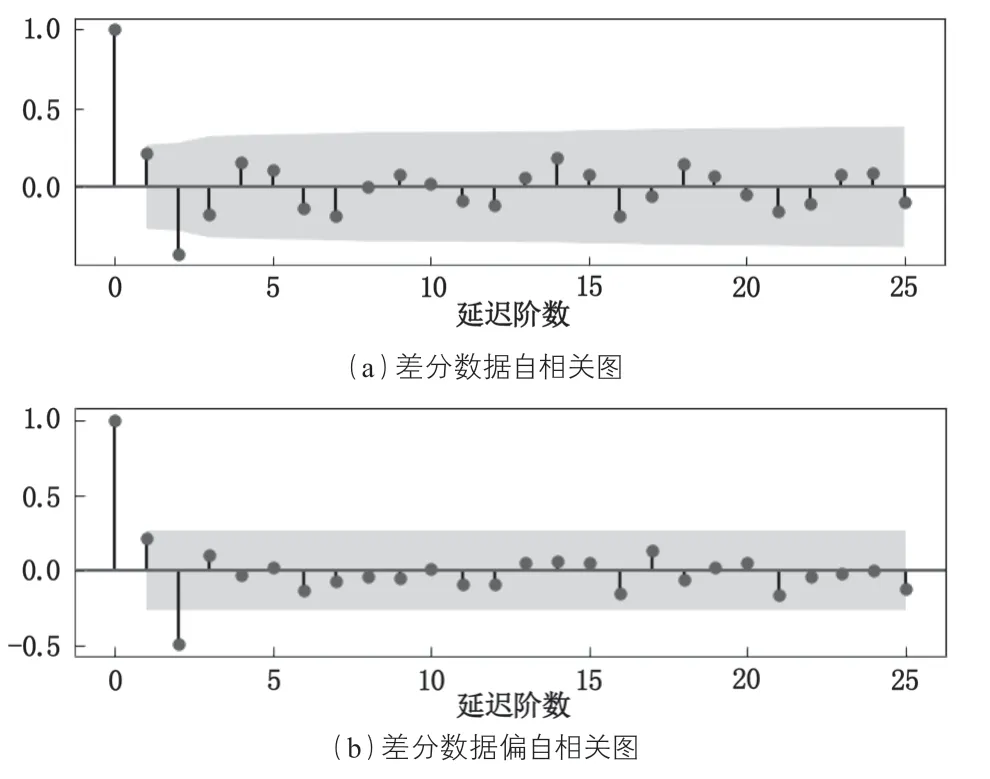
图8 差分数据自相关和偏自相关图
值得注意的是,当分析的数据量少,要建立的时序模型不多时,可以通过自相关图和偏相关图来识别模型。但是如果需要分析的监测数据量较大、监测点较多时,采用人工方法逐个识别模型,这样的工作量很大。这时,不妨直接依据 BIC 准则,借助计算机程序,能够自动、快速地求出 BIC 为最小值时所对应的 p,q 值。这样对结果可能会稍有偏差,但是能节约大量时间,有利于实现对监测数据的自动化分析。
BIC 准则是拟合精度与未知参数个数的加权函数,当 BIC 函数值达到最小时所对应的模型即为最优模型,如式(5)所示。

式中:L 为模型的极大似然估计值;K 为模型未知参数个数;N 为观测值数量。
运用 BIC 准则确定模型为ARMA(2,0),然后对模型的残差进行白噪声检验。构造 QLB检验统计量,结果表明一阶延迟的 QLB统计量 P 值为 0.649,大于显著性水平α=0.05,所以判定该残差序列是白噪声,该模型合理。
最后采用最小二乘法对模型参数进行估计,确定模型表达式,如式(6)所示。
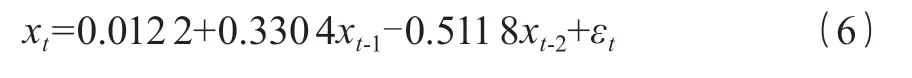
根据建立的 ARMA(2,0)模型拟合原始数据,拟合和预测结果如图9 所示(虚线为原始数据,实线为拟合预测数据,阴影部分代表预测值 95 % 置信区间)。
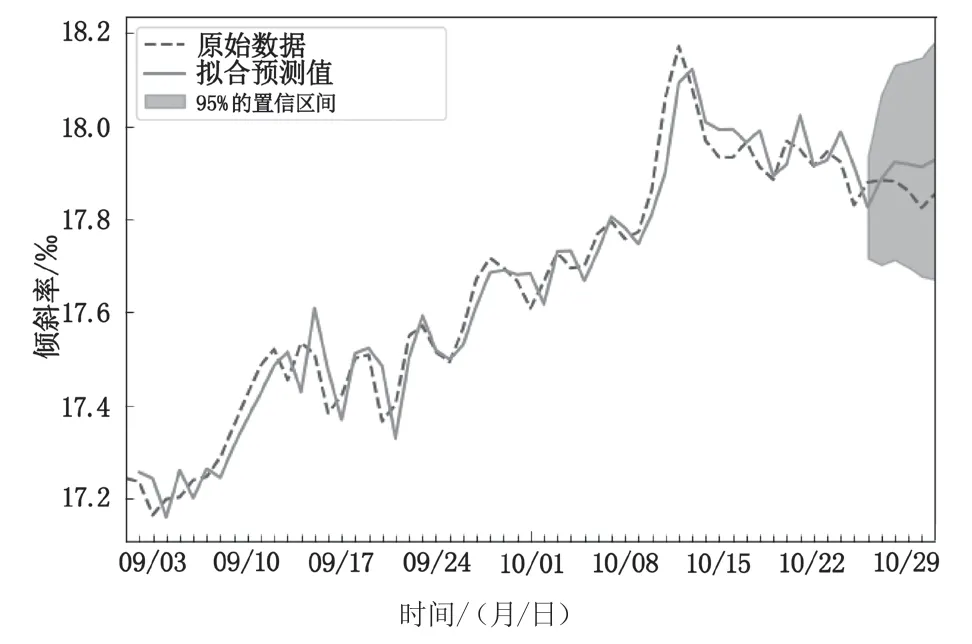
图9 原始数据与拟合预测数据对比图
后 6 期倾斜数据的预测值如表2 所示,模型的拟合和预测有较高的精度,实测值基本在预测值 95 % 的置信区间内,同时随着预测期数的增加,预测误差有增大的趋势。
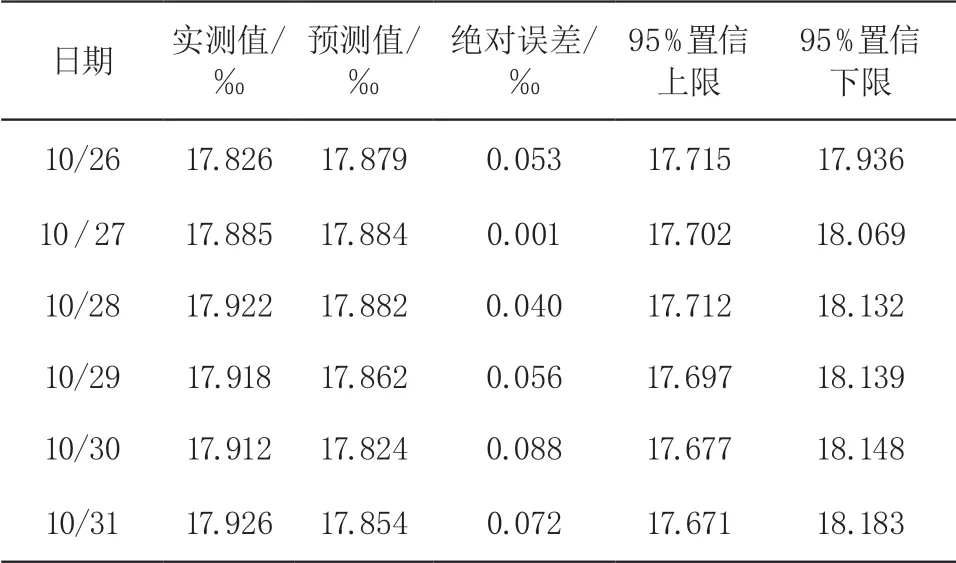
表2 时间序列分析预测结果
4 结 论
为了能够充分利用海量的监测数据,本文以某居民楼倾斜监测为例,对数据预处理和时间序列分析方法进行了研究,得到以下结论。
1)对房屋监测数据的预处理可以提高数据分析的质量和效率。
2)依据最小信息准则通过程序可以实现对时间序列模型的自动定阶,从而实现对监测数据的自动化分析。
3)在进行时间序列分析时,不仅仅要求出具体的预测值,更要得到预测值合理的置信区间。如果下一期的实测数据超过了这个置信区间,可视为异常情况,应当引起分析人员的注意。
4)时间序列模型具有较高的短期预测精度,预测精度会随着预测期数的增加而下降。因此在实际监测过程中,应根据新的监测数据及时更新模型,从而提高预测精度,及时做出预警。Q
